随机森林(RF)算法是一种分类模型,其本质是将Bagging算法和random subspace算法结合起来[1-3],通过构造多棵决策树分类器对测试样本进行分类,然后对这些决策树采取投票选取机制确定最终的分类结果.由于随机森林模型对噪声和异常值的容忍度较高,且随机森林直接通过数据进行分类,不需要分类样本的先验知识,因此可省略数据预处理的工作.随机森林算法自提出之后,被广泛地运用于数据挖掘与分类问题中[4-6].
针对随机森林算法中存在的一些问题,学者们提出了不同的方案,对随机森林算法进行改进.文献[7]从选取特征、训练样本等多个方面对随机森林进行改进,提升了训练准确率.文献[8]提出了基于生存树的随机森林模型(RSF),证明了随机生存森林对于高维样本的分类能力大于普通随机森林.文献[9]将分位数回归理论引入随机森林中,提出了分位数回归森林(QRF).在处理生长较差的决策树方面,文献[10]将随机森林算法中每棵决策树按分类性能进行排序,并淘汰掉分类性能差的决策树.但此方法的弊端在于容易淘汰掉仅对某一类别分类较好的决策树,从而影响该类别最终的分类效果.文献[11]提出了加权投票的概念,但其权值的计算方式不够优秀,很容易出现特别大的权值,从而使随机森林的投票都集中于较少的几棵树.随后,文献[12]将以上两种方法相结合,采用out-of-bag准确率作为决策树投票权重并保留70%的决策树.此方法的弊端在于每棵决策树out-of-bag样本不同从而导致投票不能保证其公平性.此外,至今为止较少有文献提及随机森林中各参数对模型的影响,决策树棵数或剪枝阈值的选取也没有理论上的支持,通常只能靠经验选取.
为解决以上问题,本文提出了一种基于粒子群算法优化的加权随机森林算法(PSOWRF),采用粒子群算法对随机森林模型进行优化,通过迭代优化的方式选取决策树棵数、剪枝阈值等参数.同时,为解决投票权重问题,本文从训练样本中提取出一部分样本,作为预测试样本,用来计算每棵决策树的权值,从而保证其投票的公平性.而本文对权值的计算方式加以简化,仅采用预测试样本的分类正确率作为每棵决策树的权值.其原因在于过于复杂的权值计算方式会极大地增加训练时间,而采用较为简单的正确率加权方法,经过粒子群算法优化之后,同样可保证其分类精确度.
1 决策树算法 1.1 ID3算法随机森林算法是由多棵决策树分类器构成,故在研究随机森林算法之前,需要对决策树有一定的了解.目前有很多种决策树生成算法,但最有影响力的是Quinlan的ID3算法.该算法在决策树中引入信息论的概念,并定义了信息增益.ID3算法的原理如下所示:假设样本S可按照目标属性分成c个不同的类别,则其分类的熵的定义为
| $ Entropy\left( S \right) = \sum\limits_{i = 1}^c { - {p_i}{\rm{lo}}{{\rm{g}}_2}{p_i}} , $ | (1) |
其中:pi为目标属性的第i个值所对应的样本在总样本S中所占的比例.
以上定义的分类熵可作为样本S的纯度判别标准,即Entropy(S)=0表示样本S属于同一种类别.根据此定义,可进一步引伸出样本S中决策属性A的信息增益Gain(S, A)的定义为
| $ Gain\left( {S, A} \right) = Entropy\left( S \right)-\sum\limits_{v \in V\left( A \right)} {\frac{{|{S_v}|}}{S}} Entropy({S_v}), $ | (2) |
其中:V(A)是决策属性A的值域,|Sv|是属性A的值为v的样本数量,|S|是总样本数量.
ID3算法就是每次都选取拥有最大信息增益的属性作为其分类属性进行分类,而分类属性临界值的选取也要最大化信息增益,直到所有结点的分类熵值为0.若样本的所有属性均参与分类后分类熵仍大于0,则返回该样本中目标属性的众数所对应的分类作为该样本最终的分类结果.
1.2 C4.5算法ID3算法虽可正确地进行分类,但仍存在许多问题.ID3算法只能对离散的数据进行分类,无法处理连续数据.且ID3算法没有剪枝的步骤,甚至可能导致每个叶结点只包含一个样本,产生过拟合现象.C4.5算法是对ID3算法的一个改进,它采用信息增益率而非信息增益来选择决策属性.信息增益率的定义为:
| $ GainRatio\left( {S, A} \right) = \frac{{Gain\left( {S, A} \right)}}{{\sum\limits_{i = 1}^c {\frac{{|{S_i}|}}{S}{\rm{lo}}{{\rm{g}}_2}\frac{{|{S_i}|}}{S}} }}. $ | (3) |
此外,C4.5算法还加入了前剪枝的步骤.即在分类过程中,当某集合的样本数小于一个给定的阈值ε时,就直接将此集合看作一个叶结点,然后返回目标属性的众数作为分类结果.阈值ε直接决定了决策树是否会出现过拟合现象或者出现分类不准确,但ε只能凭经验选取,并无理论上的支持.
2 随机森林模型及其优化 2.1 随机森林模型随机森林模型的实质是一个有多棵互不相关决策树的分类器.每棵决策树均采用Bootstrap方法进行采样,然后再从所有的M个决策属性中随机挑选出m个属性进行分类.在整个训练过程中,一般m的取值不变.训练完成后,当测试样本输入时,每棵决策树均对测试样本进行分类,并采取投票的方法决定该测试样本的最终分类结果.假设对于一个测试样本x,第l棵决策树的输出为ftree, l(x)=i,i=1, 2, …, c,即为其对应的类别,l=1, 2, …, L,L为随机森林中的决策树棵数, 则随机森林模型(RF)的输出为
| $ {{f}_{\text{RF}}}\left( x \right)=\underset{i=1,2,\ldots ,c}{\mathop{\text{arg}\ \ \text{max}}}\,\{I({{f}_{\text{tree},l}}\left( x \right)=i)\}, $ | (4) |
其中:I(·)表示满足括号中表达式的样本个数.
2.2 随机森林模型加权在传统的随机森林模型中,每棵决策树在投票时权重都相等,但又不能保证每棵决策树的分类精度一致.因此,总会有一些训练精度不高的决策树投出错误的票数,从而影响了整个随机森林的分类能力.为了降低训练精度不高的决策树对整个模型的影响,本文提出了一种加权随机森林模型.其核心是将训练样本分为两部分:一部分作为传统随机森林模型的训练样本,对所有的随机数进行训练;另一部分为预测试样本,在训练完成之后,对每棵决策树分别进行测试,并计算其分类正确率,
| $ {w_l} = \frac{{{X_{{\rm{correct}}, l}}}}{X}, l = 1, 2, \ldots, L, $ | (5) |
其中:Xcorrect, l为第l棵树分类正确的样本数,X为预测试样本数.
将此正确率作为对应决策树的权重,每棵决策树在进行投票时,都要乘以此权值.则加权随机森林模型(WRF)的输出为:
| $ {{f}_{\text{WRF}}}\left( x \right)=\underset{i=1,2,\ldots ,c}{\mathop{\text{arg}\ \ \text{max}}}\,\{\sum\limits_{l\in L,{{f}_{\text{tree},l}}\left( x \right)=i}{{{w}_{l}}}\}. $ | (6) |
以上算法中,剪枝阈值ε、决策树棵数L、预测试样本数X、随机属性个数m等参数对整个模型的输出具有一定的影响.但所有参数均需要通过经验选取,并没有理论上的支持.粒子群算法通过对鸟类捕食行为进行模拟,能够快速地选取最优解.本文通过将粒子群算法引入模型,对加权随机森林算法中的参数进行迭代优化,最终达到了较好的分类效果.
粒子群优化加权随机森林算法的步骤如下:
Step1 确定算法的参数,随机设定出剪枝阈值ε、决策树棵数L、预测试样本数X、随机属性个数m的初值;
Step2 采用Bootstrap算法采样,随机生产L个训练集,并在每个训练集中选出X个预测试样本;
Step3 利用每个训练集剩下的样本分别生成决策树,共L棵,在生成过程中,每次选择属性前,均从全部属性中选出m个属性作为当前结点的决策属性;
Step4 当结点内包含的样本数少于阈值ε时,将该结点作为叶结点,并返回其目标属性的众数作为该决策树的分类结果;
Step5 当所有决策树生成后,对每棵决策树进行预测试,并利用式(5)计算其权值;
Step6 利用式(6)计算出模型的分类结果;
Step7 将分类结果作为适应度值,采用粒子群算法对Step1中提到的参数进行迭代优化,确定最终模型的参数.
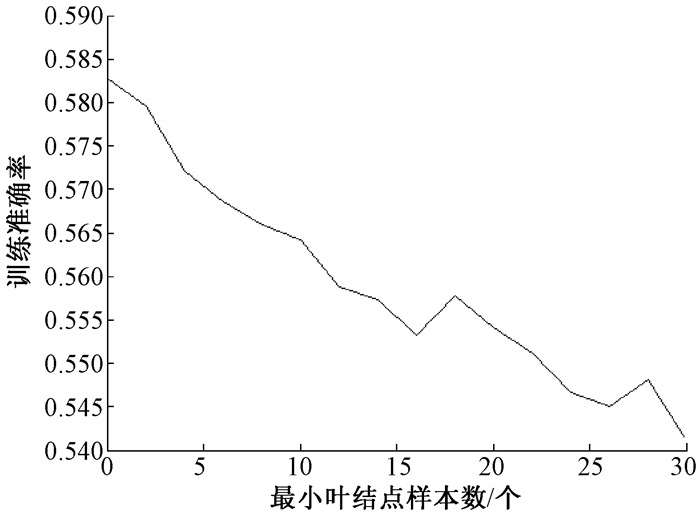
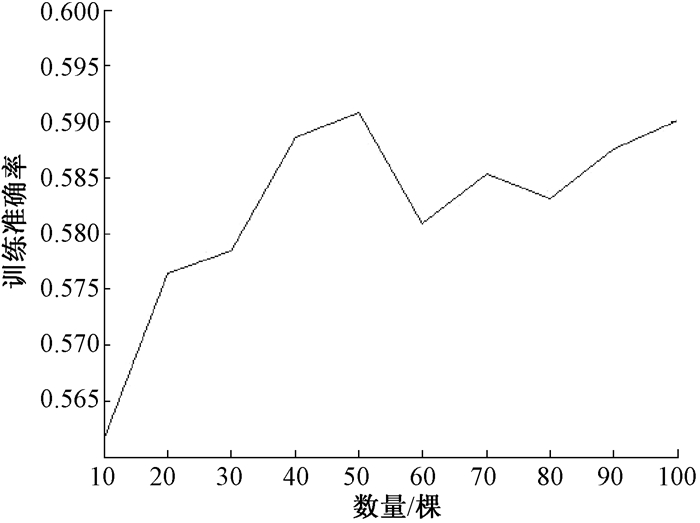
3 实验验证及分析本文中用到的实验数据均来自于加利福尼亚大学的UCI数据库,并选取了其中Abalone、Banks、Car Evaluation、Letter、Wine Quality和Yeast共6个数据集.为了验证模型参数对加权随机森林算法分类能力的影响,本文选取Wine Quality数据集作为验证数据集,分别对剪枝阈值ε和决策树棵数L进行验证.实验1对剪枝阈值ε在0到30之间进行取值,并记录所得分类准确率.实验1的结果如图 1所示.实验2对决策树棵数L分别取值为10到100之间的10的整数倍,其结果如图 2所示.
|
图 1 剪枝阈值对分类性能的影响 Figure 1 Effect of pruning threshold on test accuracy |
|
图 2 决策树棵数对性能的影响 Figure 2 Effect of tree's number on test accuracy |
通过图 1可看出,随着剪枝阈值ε的不断增加,分类性能呈现一个下降的趋势.因此对于数据集Wine Quality来说,剪枝阈值ε为0可取得最高的分类准确率.从图 2可发现,决策树棵数在50以后,分类的准确率在0.59左右开始波动.故对于数据集Wine Quality,最佳的决策树棵数为50.因此可说明,Step1中提及的参数对模型的分类性能具有一定的影响.为保证选取到最优值,本文采用粒子群算法对模型进行优化,提出粒子群优化加权随机森林算法(PSOWRF),并在6组数据集上进行测试.将其训练结果与文献[12]中提到的普通加权随机森林(WRF)、分位数回归森林(QRF)、随机生存森林(RSF)、传统随机森林(RF)、C4.5决策树分类器(DT)、支持向量机(SVM)和BP神经网络等传统分类器进行对比,结果如表 1所示.表 1中记录了所有算法对6个数据集的平均分类正确率.每个数据集名之后括号中的两个数字分类代表了该数据集的属性个数和类别个数.
|
|
表 1 不同算法分类性能比较 Table 1 The comparison of different algorithms |
根据表 1可以得到,PSOWRF在Abalone、Car Evaluation、Letter 3个数据集上均取得了最优分类正确率,同时在Banks和Wine Quality两个数据集上的分类正确率与最优正确率无统计学差异.对于Abalone数据集,PSOWRF取得了最优结果,WRF、RSF、QRF和SVM的表现情况相差不大,均比RF、DT和BP算法更加优秀.对于高维的数据集Banks和Wine Quality,RSF充分展示了其对高维数据的分类能力,取得最优解,而PSOWRF也表现良好,与RSF无明显差异.对于数据集Car Evaluation,PSOWRF和QRF、SVM同时取得较好的分类结果,优于其他算法.对于多类别的Letter数据集,PSOWRF远远领先于其他算法,取得最优结果.最后,对于Yeast数据集,SVM算法超过了所有的随机森林算法及改进.综上所述,本文所提出的PSOWRF算法在除Yeast之外的5个数据集上均能够取得不错的表现,而且在Abalone和Letter数据集上要明显优于其他算法.
4 结论本文对随机森林模型的投票机制做出了一定的改进,从训练样本中提取出一部分预测试样本,并将每棵决策树对预测试样本的分类正确率作为其投票权值.为保证模型参数能够取得最优值,本文还利用粒子群算法对模型进行优化,提出了基于粒子群优化的加权随机森林算法.该算法在6组实验数据集上均取得了良好的结果.在今后的工作中,我们将会对随机森林模型的采样机制进行研究.通过对比不同采样算法对分类性能的影响,决定出最优的采样算法,而不局限于仅用Bootstrap算法进行采样.
| [1] |
BREIMAN L. Random forests[J]. Machine learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 (  0) 0) |
| [2] |
BREIMAN L. Bagging predictors[J]. Machine learning, 1996, 24(2): 123-140. (  0) 0) |
| [3] |
HO T. The random subspace method for constructing decision forests[J]. IEEE transactions on pattern analysis and machine intelligence, 1998, 20(8): 832-844. DOI:10.1109/34.709601 (  0) 0) |
| [4] |
李欣海. 随机森林模型在分类与回归分析中的应用[J]. 应用昆虫学报, 2013, 50(4): 1190-1197. (  0) 0) |
| [5] |
林成德, 彭国兰. 随机森林在企业信用评估指标体系确定中的应用[J]. 厦门大学学报(自然科学版), 2007, 46(2): 199-203. (  0) 0) |
| [6] |
杨帆, 林琛, 周绮凤, 等. 基于随机森林的潜在k近邻算法及其在基因表达数据分类中的应用[J]. 系统工程理论与实践, 2012, 32(4): 815-825. (  0) 0) |
| [7] |
ROBNIK-IKONJA M. Improving random forests[C]//15th European Conference on Machine Learning. Italy, 2004.
(  0) 0) |
| [8] |
ISHWARAN H, KOGALUR U B, BLACKSTONE E H, et al. Random survival forests[J]. Journal of thoracic oncology official publication of the international association for the study of lung cancer, 2008, 6(12): 1974-1975. (  0) 0) |
| [9] |
NICOLAI M. Quantile regression forests[J]. Journal of machine learning research, 2006, 7(2): 983-999. (  0) 0) |
| [10] |
CROUX C, JOOSSENS K, LEMMENS A. Trimmed bagging[J]. Computational statistics & data analysis, 2007, 52(1): 362-368. (  0) 0) |
| [11] |
AMARATUNGA D, CABRERA J, LEE Y S. Enriched random forests[J]. Bioinformatics, 2008, 24(18): 2010-2014. DOI:10.1093/bioinformatics/btn356 (  0) 0) |
| [12] |
XU B, GUO X, YE Y, et al. An improved random forest classifier for text categorization[J]. Journal of computers, 2012, 7(12): 2913-2920. (  0) 0) |
 2018, Vol. 50
2018, Vol. 50

