2. 山东科技大学 电子通信与物理学院 山东 青岛 266590
2. College of Electronic Communication and Physics, Shandong University of Science and Technology, Qingdao 266590, China
在地质勘探中,钻孔内壁上由于岩性不同等原因而产生的纹理脉络信息对于了解地质情况具有重要意义.对于地质结构没有被揭露的部分,需要打钻孔进行观测.取岩心法是常用的方法,但此方法工作量大,成本高,且对软弱层、破碎层等松散结构取芯率低,易破坏纹理结构.随着光学技术的发展,摄像技术被应用到地质勘探中,利用钻孔摄像装置,可以直观清晰地对钻孔内地质情况进行观测,弥补了取岩心法的不足.钻孔摄像技术经历钻孔照相、钻孔摄像和数字光学成像3个发展阶段,其中钻孔摄像和数字光学成像为目前主流设备[1].钻孔摄像以前视钻孔窥视仪为代表,其结构简单,利用广角摄像头对钻孔进行前视摄像,成像特征符合人眼观察习惯,可直接对孔壁纹理脉络进行定性判断,该技术已广泛应用于地质勘探中,但此技术无法对钻孔内壁信息进行定量分析[2].数字光学成像是在前视窥视仪的基础上,在镜头前方加装锥形反射镜,将孔壁信息反射到镜头成像,由此得到圆环状图像,此类图像由于经过光学反射,图像畸变较大,不易直接观察,须转换到直角坐标系下才能观察分析.数字光学成像系统成像清晰,代表了钻孔摄像技术的最高水平[1],但其结构复杂,需要电子罗盘等装置的辅助,在水平倾斜孔等场景下应用效果差,且价格较高.前视钻孔窥视仪虽然在技术上较简单,但其应用灵活,结构简单,在很多场景下应用广泛[2-4].
本文将数字图像处理技术与前视钻孔窥视仪结合,既突出了前视摄像的灵活,又运用图像处理技术弥补了其在定量分析上的不足,其利用简易装置获取图像信息,采用同心圆环展开算法和图像灰度特征相似度最大匹配准则处理图像,得到的全景拼接图符合观察需要,且此过程具有速度快、准确度高的特点.
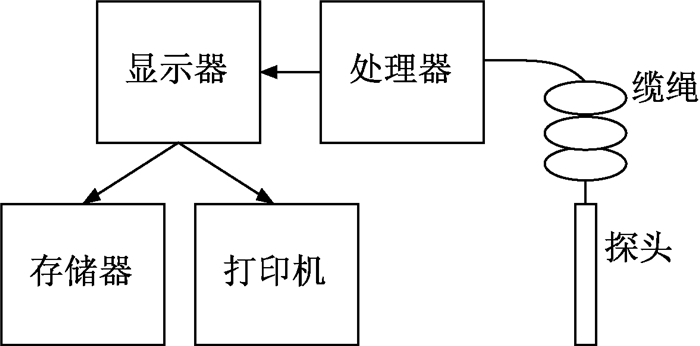
1 前视全景图采集 1.1 硬件结构硬件是进行相关勘探工作的前提和基础,主要结构有探头(摄像头、光源等)、深度仪、缆绳以及地面上的图像采集卡和主机.前视全景图像采集和处理硬件系统如图 1所示.
|
图 1 前视全景图像采集和处理硬件系统 Figure 1 The hardware system of forward panoramic image acquisition and processing |
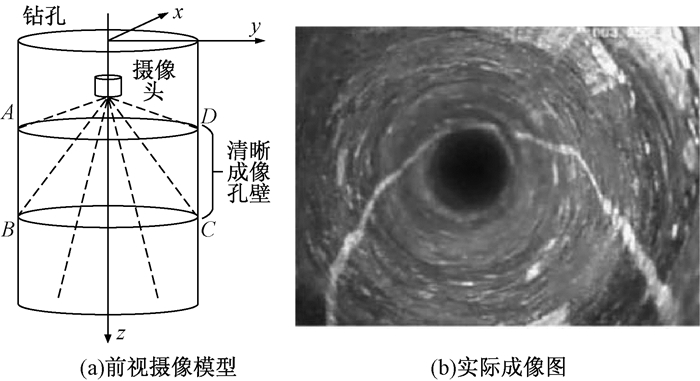
利用广角摄像头,配合光源并结合深度仪,可摄取孔壁前视全景图像.广角摄像头可在较大的角度内摄取图像或视频,但视角过大的超广角镜头焦距短且会造成较大的图像畸变,不利于观察及后期的处理.前视摄像模型及实际成像图如图 2所示.
|
图 2 前视摄像模型及实际成像图 Figure 2 Forward camera model and actual image |
由于摄像头有固定的焦距,所以在ABCD孔壁上成像清晰,BC圆以下的区域也有成像,但其受摄像头焦距及光亮度的影响,信息度低.此成像过程模拟人眼成像,可直接获取钻孔内壁部分信息.同时,经过展开拼接等图像处理技术,还可进行精确的定量分析.
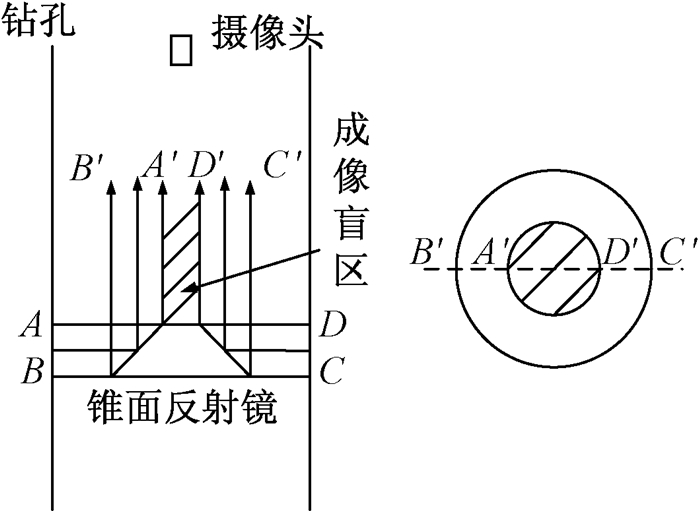
数字光学成像是在前视成像的基础上,加装锥面反射镜,将孔壁经过反射镜成像,锥面镜中心区域为成像盲区,此方法可以提高成像的精度,但图像发生很大畸变,无法直接观察,须经过展开与拼接处理方可进行分析,因此产生了很大的限制.光学成像模型如图 3所示.
|
图 3 光学成像模型 Figure 3 Optical image model |
前视视频具备定性观测条件,但如需进行更为精确的定量分析,首先须进行展开处理.由于成像原理的特点,前视摄像头获取到的图像无直接的成像边界,直观的只有由近到远的孔壁,以及远端的低光区域.因此,需要运用图像处理技术,自动定位圆心并设置合理的半径,进而划定环形区域,为后续的图像展开奠定基础.由于远端低光而形成的黑色区域,近似圆形,且从灰度级上分析,其区域值与其他区域的值有明显的区分,可利用此特点进行圆心定位.
预处理阶段利用中值滤波及灰度调整,突出远端低光区域,同时增强孔壁灰度值,结果如图 4(a)所示.二值化处理如图 4(b)所示,结合取反并去除小面积,得到如图 4(c)所示的图像.对预处理后的图像近圆形区域求取质心,即可得到精确度较高的圆心位置.本文手动设置了半径,以截取得到环形区域,结果如图 4(d)所示.

|
图 4 图像处理过程 Figure 4 Image processing |
全景图像展开算法主要包括基于光学变换的光路追踪法及其改进算法和基于数学变换的同心圆环展开法[5].本文采用改进的坐标转换算法,结合插值算法,实现了对环形区域的快速展开.
同心圆环展开原理如图 5所示,将图中半径为R′的虚线圆,沿一定的初始相位展开为直线,P(x,y)与环形区域中的P′(x,y)等同于极坐标与直角坐标的转换关系,即

|
图 5 同心圆环展开原理 Figure 5 Concentric ring expansion principle |
| $ \left\{ \begin{array}{l} x = {x_0} + \left( {r + y} \right) \times \sin \;\alpha, \\ y = {y_0} + \left( {r + y} \right) \times \cos \;\alpha, \end{array} \right. $ | (1) |
式中:α为弧长与半径的比值;(x0,y0)为O点坐标.
展开区域的高度为R-r,宽度为2πR′,其中R′为r至R间的任意值,在实际应用中可任意设定.通过极坐标转换公式可看出,展开图中的点与原图中的点存在固定的对应关系,相位角α在0~2π间变化,由正、余弦函数特性可知,只需计算其1/4区域的值即可得到全区间的函数值,利用此特性可缩短坐标求取时间,提高运算效率.
2.2 图像插值在坐标运算中,α可取0~2π间的任意值,因此,得到的正、余弦值为浮点数,由于图像像素点的位置均为整数点,求取到的浮点坐标不存在像素值,需要进行插值运算,近似得到此坐标对应的像素值.最临近插值和双线性插值为常用的方法.最临近插值原理如图 6所示,即将距离浮点坐标最近的整数点坐标的像素值赋值于浮点坐标.由于此方法在临近像素值有较大改变时,会产生锯齿状效果,成像粗糙.因此,采用双线性插值,以达到理想的清晰度.最临近插值与双线性插值效果如图 7所示,可以看出,双线性插值较最临近插值在细节上更为平滑,不会出现锯齿状效果.

|
图 6 最临近插值原理 Figure 6 The nearest interpolation principle |

|
图 7 最临近插值和双线性插值效果 Figure 7 Results of the nearest interpolation and bilinear interpolation |
线性插值算法根据(x, y)点的4个相邻点的灰度值,分别在x、y两个方向上进行插值,计算出f(x, y)的值,形成的插值函数为双曲抛物面方程
| $ f(x, y)=αx+by+cxy+d. $ | (2) |
插值过程由此抛物面和4个临近点进行拟合.首先在x方向上作线性插值,对上端的两个顶点进行线性插值,得
| $ f(x, 0)=f(0, 0)+x[f(1, 0)-f(0, 0)]. $ | (3) |
类似的,对于底端的两个顶点,有
| $ f(x, 1)=f(0, 1)+x[f(1, 1)-f(0, 1)]. $ | (4) |
最后,在y方向上作线性插值,有
| $ f(x, y)=f(x, 0)+y[f(x, 1)-f(x, 0)]. $ | (5) |
综合(3)~(5) 式,展开等式并合并同类项,得
| $ f(x, y)=x[f(1, 0)-f(0, 0)]+y[f(0, 1)-f(0, 0)]+\\ xy[f(1, 1)+f(0, 0)-f(0, 1)-f(1, 0)]+f(0, 0). $ | (6) |
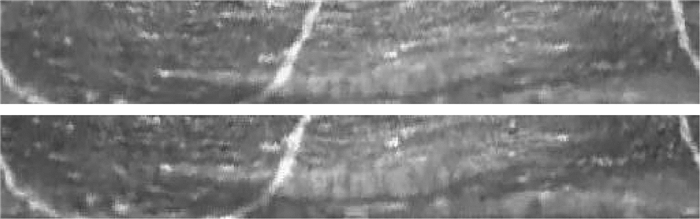
双线性插值已经考虑到(x,y)点的直接相邻点对它的影响,一般可得到较满意的结果,但这种方法具有低通滤波的特性,使高频分量受到损失,图像轮廓有一定的模糊,如果需要得到更精确的插值效果,应采用高阶插值[6].图 8为图 2(b)的展开效果,运用了双线性插值法.
2.3 图像匹配拼接图像序列通过加入时间属性实现了对拍摄场景的空间和时间上的信息融合存储,序列中的每帧图像只反映了某一时间、空间的局部信息,而序列整体在时间、空间上又有很大的冗余,因此,利用图像拼接技术可减少表示场景所需数据量,提高利用效率.
将展开后的矩形区域拼接成完整的全景图,图像匹配为此过程的前提和关键.其方法大致可分为两类:一类为基于图像灰度信息的匹配; 另一类为基于图像特征的匹配.基于图像特征的匹配主要代表为基于特征点的图像匹配,此类方法匹配精度高,且具有平移旋转不变性等优点,但运算时间长,资源消耗大,效率低.根据孔壁图像灰度变化单一且图像复杂度低的特点,采用基于图像灰度信息的匹配方法,能够快速准确地完成图像匹配.
由于前视摄像探头在钻孔内会做轴向运动和旋转运动,因此,表现在矩形展开图上即为x和y轴方向上的平移.进行图像匹配,即匹配出两轴方向上的偏移量,利用横向偏移量修正x轴方向上的平移,再利用纵向偏移量进行拼接,图像偏移如图 9所示.

|
图 9 图像偏移 Figure 9 Images deviation |
基于灰度投影法的图像灰度信息匹配方法,即把二维的图像灰度值投影到已知坐标轴,从而形成一维数据,再在此一维数据上进行匹配,此过程通过降维来达到提高匹配速度的目的[7].例如,某t时刻的图像f,其尺度为M×N,在x轴方向上及y轴方向上做灰度投影并计算均值,可表示为
| $ \left\{ \begin{array}{l} {F_t}\left( {{x_0}} \right) = \frac{1}{N}\sum\limits_{y-1}^N {{f_t}\left( {{x_0}, y} \right), {x_0} = 1, 2, \cdots, M, } \\ {F_t}\left( {{y_0}} \right) = \frac{1}{M}\sum\limits_{x-1}^N {{f_t}\left( {x, {y_0}} \right), {y_0} = 1, 2, \cdots, N, } \end{array} \right. $ | (7) |
式中:ft(x0,y)和ft(x,y0)分别为t时刻图像的灰度值.垂直灰度投影示意图如图 10所示.

|
图 10 垂直灰度投影示意图 Figure 10 Vertical gray level projection |
以在y轴方向上的投影匹配为例,利用灰度直方图选取灰度特征变化明显的区域S1={s1,s2,…, si|1 < i < M}作为参考域,其序列长度为|S1|,在前一帧y轴方向上的灰度投影区间内建立比对域S2={s1, s2, …,sM},其序列长度为|S2|,|S1| < |S2|.结合参考域和比对域建立相似性度量模型C={S1,S2},统计S2内与S1等长序列的相似度,并比对出度量最大值所对应的序列,即可得出运功参数.相似度计算[8]为
| $ r = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i}-\bar x} \right) \times \left( {{y_i}-\bar y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i}-\bar x} \right)}^2} \times {{\left( {{y_i} - \bar y} \right)}^2}} } }}. $ | (8) |
得到位移匹配参数后,即可进行全景图的生成.由于亮度变化和灰度变化等因素的干扰,直接生成的全景图会有明显的缝隙,影响观测,可在拼接过程中运用加权融合方法,按照一定的权值比例进行融合[9],此方法适用于对细节信息要求严格的场合.设两幅图像为i1和i2,拼接后的图像为i3,权值因子为d(0 < d < 1), 有i3=d×i1+(1-d)×i2;也可在拼接后利用滤波处理,模糊缝隙及噪声,此方法适用于以分析全局信息为主的情况.利用采集的钻孔孔壁图像以及模拟的孔壁模型图像进行实验,实验平台为Matlab,全景图如图 11所示.后期可结合相关设备,精确得到地质构造信息.

|
图 11 全景图 Figure 11 Panoramic image |
利用全景摄像技术得到钻孔图像,并通过数字图像处理技术进行展开与拼接,即可得到大范围钻孔孔壁全景图,通过此全景图可对裂隙、分层和岩性等构造信息进行定量分析.此方法弥补了前视成像设备只能定性分析孔壁信息的不足,在地质勘探中具有较高的价值.后续的工作将围绕提高相关性匹配及进一步消除拼接缝隙展开,并控制过程时间,以达到实时处理的效果.
| [1] |
王川婴, LAWKT. 钻孔摄像技术的发展与现状[J]. 岩石力学与工程学报, 2005, 24(19): 3440-3448. DOI:10.3321/j.issn:1000-6915.2005.19.006 (  0) 0) |
| [2] |
王川婴, 葛修润, 白世伟. 前视全景钻孔电视及其应用[J]. 岩石力学与工程学报, 2001, 20(S1): 1687-1691. (  0) 0) |
| [3] |
于景良, 王德福. 全景式孔内彩色电视系统的研制及其应用[J]. 大坝观测与土工测试, 1996, 20(4): 30-32. (  0) 0) |
| [4] |
刘勇. 电子窥视仪在煤矿中的应用[J]. 煤矿开采, 2006, 11(1): 54-55. (  0) 0) |
| [5] |
祝小蜜, 张晓頔. 一种全景图像展开的新方法[J]. 科技资讯, 2014(2): 19-20. (  0) 0) |
| [6] |
曹茂永. 数字图像处理[M]. 北京: 北京大学出版社, 2007.
(  0) 0) |
| [7] |
高晓峰, 史朝辉. 一种改进的基于灰度投影的图像匹配算法[J]. 航空计算技术, 2012, 42(6): 85-87. (  0) 0) |
| [8] |
朱扬勇, 戴东波, 熊赟. 序列数据相似性查询技术研究综述[J]. 计算机研究与发展, 2010, 47(2): 264-276. (  0) 0) |
| [9] |
王成良, 杨鹏, 蔡耀泽, 等. 孔壁全景图获取中的图像拼接技术研究[J]. 计算机应用, 2010, 30(2): 344-347. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49