城市的飞速发展使人们的出行更加方便,但同时也带来了交通拥堵、资源浪费和人口密集的问题。同时,随着基于位置技术服务(location based services,LBS)的普及和设备计算能力的提高[1],城市居民的行为将被传感器收集[2],以生成大量的人类活动数据集,使得探索现代城市中各种社会行为规律,帮助解决快速现代化所带来的各种城市问题成为可能。
由于城市处于复杂并高度动态的环境下,人群活动行为呈现着不同的规律,如何对人群活动进行解释和预测存在着一定难度。本文首先对城市中的人群活动数据进行预测和分析,基于城市人群活动数据对城市进行区域划分,据此提取城市人群活动模态,提出一种基于多模态融合的人群流量预测算法,通过提取城市区域之间的多重相关性来建立多模态表示,对于各种模态进行融合从而提高预测的准确性。本文的贡献如下:
1) 为了捕获城市区域之间的多种相关性,使用图卷积算子探索区域之间的相关性以建立多模态并构建了四个相关性图,包括区域间距离图、流量相似性图、流量交互性图和区域特征相似性图;
2) 使用带有注意力机制的卷积神经网络模型对不同的模态图进行卷积,并在此基础上进行多模态融合,更好地捕获区域之间的差异;
3) 通过对上海市真实数据集的实验,证明了所提出的模型可以准确预测人群活动流量。
1 相关工作城市流量预测是关乎城市未来发展的重要问题。它主要是通过采集历史数据并用某种数学模型来预测未来的流量情况。交通预测有几种通用方法,包括回归和时间序列分析。另外由于城市环境下人类活动数据可以应用于多种场景,在流量预测方面通过特征可划分为三类。
1.1 基于统计和机器学习方法的城市数据流量预测算法城市数据流量预测算法大多基于时空特征,由于这些研究通常集中于特定类型的数据流量,算法简单。文献[3]提出一种新颖的多视图子空间聚类算法,适用于小量数据集,当涉及数据种类多,人类活动数据过于复杂的情况下,时间和空间复杂度较高,算法的成本消耗大[4]。
1.2 基于概率图模型的城市数据流量预测算法基于概率图模型的城市数据流量预测算法主要应用于数据集单一、内部联系紧密的情况,局限性较大。文献[5]提出了一种基于动态集群的过度预测框架来预测站点式共享自行车的流量。通过建立一个加权相关网络来模拟站点之间的关系,并将具有相似自行车使用模式的相邻车站动态分组为集群。文献[6]使用耦合隐马尔可夫模型(coupled hidden Markov model, CHMM) 对从高速公路的环路检测器所收集的数据进行建模。通过期望最大化(expectation-maximization, EM)算法来拟合模型参数。
1.3 基于深度学习的城市数据流量预测算法随着数据规模的增长和设备计算能力的提高,深度学习得到了迅速发展。文献[7]提出图卷积神经网络(graph convolutional network, GCN) 的概念,该方法将光谱图理论与深层神经网络联系在一起。文献[8]提出了用于自行车流量预测的多图卷积网络,但是该方法没有考虑到自行车流量区域其他的空间相关性。文献[9]提出了一种基于数据驱动的扩散卷积递归神经网络(diffusion convolutional recurrent neural network, DCRNN)。但是,这些方法都针对特定种类的人群流,难以适应其他流量预测问题。文献[10]提出了一种使用空间图卷积为人群流量预测问题构建多视图图卷积网络模型,这种方法需要积累长时间的数据,并且很难在高度动态的城市环境中进行。
通过分析以上研究现状,现有研究工作中有大量关于城市人群活动数据的流量预测的工作,但是主要是通过解决问题中的众多约束或图形模型来执行带有一些环境变量的交通量预测。环境方面的变量很多,用户无法考虑所有这些变量,这也使优化变得极其复杂且难以解决。
2 基于多模态融合的流量预测模型城市环境中收集的数据主要由传感器收集的分散的GPS数据点组成。在城市复杂的地理环境中,无法直接用GPS数据点执行相应的建模。本文基于OPTICS (ordering points to identify the clustering structure) 算法提出了一种改进后的基于热度值的城市区域形成(heat-ordering points to identify the clustering structure, Heat-OPTICS) 算法,将城市区域划分为相同大小的网格,然后使用区域划分算法形成具有不同规模边界的城市热区(urban heat region, UHR)。
本文使用PageRank值来衡量区域活动的程度,其中PageRank值计算公式为
| $ P{R_i} = \partial \sum\limits_{j \in {\Im _i}} {\frac{{P{R_j}}}{{{\rm{ }}\mathit{out}{{\rm{ }}_j}}}} + \frac{{1 - a}}{R}, $ |
其中:outj表示第j个网格流出流量的大小;
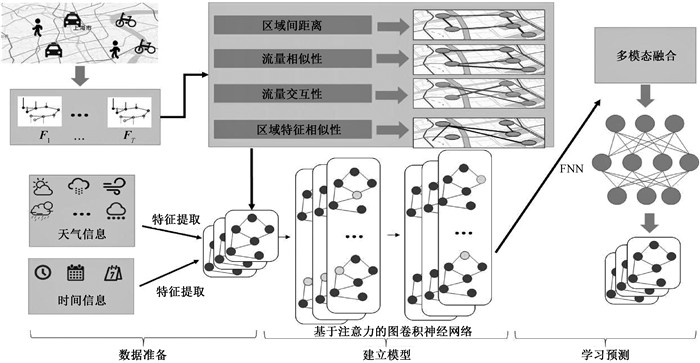
如图 1所示,本文的模型框架图包括三个部分:数据准备、模型构建以及学习预测。在数据准备过程中,城市人群流量数据以小时为间隔划分,共T个小时。通过划分市区,确定了流量预测任务是区域级别的。
|
图 1 模型框架图 Fig. 1 Model frame diagram |
整个城市用加权图G=(V,R,A)表示,其中:V和R表示节点数(根据区域划分算法划分)和边集合;A∈RV×V表示节点的邻接矩阵。其中每个节点拥有Z个属性,每个属性表示与区域相关的人群流量,设定Ft∈RV×Z从而对历史数据集以小时为时间间隔(Ft-h~Ft)来构建图信号。人群活动行为会受到天气、温度、假期和该地区兴趣点类型等因素的影响,将这些因素作为数据的补充属性。
在模型构建中,对于人群活动数据以及区域属性特征通过基于注意力机制的图卷积神经网络进行训练。为了捕获该信息城市区域之间存在的多重相关性,本文构建四个相关图:区域间距离图、流量相似性图、流量交互性图、区域特征相似性图,并使用多模态融合将这些包含有额外信息的图作为人群活动流量图的补充信息,从而更好地进行人群流量预测。
在学习和预测过程中,首先将人群活动数据应用于基于注意力机制的图卷积神经网络。对于其他相关图,使用全连接神经网络通过多模态融合来完成学习预测。本文的人群流量预测问题就是去学习函数f(),来预测未来一段时间的图信号,函数映射关系为
| $ \left\{ {{\mathit{\boldsymbol{F}}}^{t-h+1}}, {{\mathit{\boldsymbol{F}}}^{t-h+2}}, \cdots , {{\mathit{\boldsymbol{F}}}^{t}};G \right\}\xrightarrow{f(\cdot )}\left\{ {{\mathit{\boldsymbol{F}}}^{t+1}}, {{\mathit{\boldsymbol{F}}}^{t+2}}, \cdots , {{\mathit{\boldsymbol{F}}}^{t+h}} \right\}。$ |
用dist(i, j)表示网格i的中心与网格j之间的欧氏距离。随后,将网格i的热点值定义为
| $ {h_{(i, j)}} = \exp \frac{{ - \mathit{dist}{{(i, j)}^2}}}{{2\mathit{\sigma }}}, {H_i} = \sum\limits_{j \in {\rm{ }}\mathit{ne}{\mathit{i}_i}{\rm{ }}} {{h_{(i, j)}}} \times P{R_j}, $ |
其中neii表示围绕i的一组网格。显然,i周围的网格越受欢迎,Hi的热点值越高。接下来,将当前热点网格可访问的剩余网格添加到这些新群集中,并重复此过程,直到所有网格都被加入到群集并且没有创建新群集为止。算法1为Heat-OPTICS算法的伪代码。
算法1 Heat-OPTICS
Input: Grids, PRth, Maximum radius eps, Hth, Minpts
Output: center point of clusters order=[c1, c2, …, cn], UHRs
Initialization: UHRs←Ø, V←Ø, get HeatPoint, PopPoint, Q←HeatPoint
1: for each unprocessed set p of Q do
2: for g of p do
3: if g∈V then
4: Continue
5: R←Cluster (g, PopPoint, HeatPoint)
6: if |HeatPoint∩R|≤Minpts then
7: V←V∪R
8: UHRs←UHRs∪{R}
9: increase PRth, Hth, Minpts
10: get HeatPoint, PopPoint
11: Q←HeatPoint-V
12: for each x of Grids-Q do
13: computer Reachable Distance to each Point x in Order
14: if Reachable Distance < eps then
15: HOIs←x
16: return UHRs
2.2 使用相关图对区域相关性进行编码为了更好地捕获城市区域之间的空间依赖性,假设两个较近的城市区域之间有更加紧密的联系。另外,区域特征、流量频率以及流动模式的相似性对于人群活动预测也有不可忽视的影响。基于这些考虑,本文构建城市区域之间的四种相关性图。
2.2.1 构建区域间距离图在城市地区中,地理位置相近的区域会受到同一事件的影响,为此,本文构造了一个区域距离相关图Gd=(V, Rd, Ad),其公式为
| $ \mathit{\boldsymbol{A}}_{ij}^{\rm{d}} = \left\{ {\begin{array}{*{20}{l}} {{{\rm{e}}^{ - \frac{{dist{{(i, j)}^2}}}{{{b_{\rm{d}}}}}}}, }&{\mathit{dist}(i, j) \le T{h_{\rm{d}}}, }\\ {0, }&{\mathit{dist}(i, j) > T{h_{\rm{d}}}, } \end{array}} \right. $ |
其中:dist(i, j)为计算任意两个区域中心i和j之间的距离;指数函数为模拟城市区域之间的距离相关性;为了控制Ad的稀疏性,将距离阈值设置为Thd;bd的目的是将Ad调整为合适的尺寸。
2.2.2 构建流量相似性图若想在某个区域中找到人群流动模态时,可以参考其他具有相似人群流动模态的区域。为此,构造流量相似性图Gs=(V, Rs, As),具体公式为
| $ \mathit{\boldsymbol{A}}_{ij}^{\rm{s}} = \left\{ {\begin{array}{*{20}{l}} {{{\left( {{R_{ij}}} \right)}^{{b_{\rm{s}}}}},}&{{{\left( {{R_{ij}}} \right)}^{{b_{\rm{s}}}}} > T{h_{\rm{s}}}}\\ {0,}&{{{\left( {{R_{ij}}} \right)}^{{b_{\rm{s}}}}} \le T{h_{\rm{s}}}} \end{array},{R_{ij}} = \frac{{{\mathit{\boldsymbol{C}}_{ij}}}}{{\sqrt {{\mathit{\boldsymbol{C}}_{ii}}*{\mathit{\boldsymbol{C}}_{ij}}} }},} \right. $ |
式中使用协方差矩阵C来计算相关系数。另外,为了控制As的稀疏性,将距离阈值设置为Ths;bs的目的是将As调整为适当的大小。
2.2.3 构建流量交互性图从人群活动流量的历史记录中可以获取城市区域之间的交换流量。为此,构造流量交换图Gu=(V, Ru, Au),用于对两个区域之间的交易交互频率的编码。具体公式为
| $ \mathit{\boldsymbol{A}}_{ij}^{\rm{u}} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\Gamma }\left( {{\mathit{\boldsymbol{F}}_{ij}} + {\mathit{\boldsymbol{F}}_{ji}}} \right), }&{\mathit{\Gamma }\left( {{\mathit{\boldsymbol{F}}_{ij}} + {\mathit{\boldsymbol{F}}_{ji}}} \right) > T{h_{\rm{d}}}, }\\ {0, }&{\mathit{\Gamma }\left( {{\mathit{\boldsymbol{F}}_{ij}} + {\mathit{\boldsymbol{F}}_{ji}}} \right) \le T{h_{\rm{d}}}。} \end{array}} \right. $ |
其中Γ表示归一化函数,并且为了控制Au的稀疏性,设置了距离阈值为Thd。
2.2.4 构建区域特征相似性图区域之间特征的差异也会影响区域间人口活动。为此,构造区域特征图Gp=(V, Rp, Ap),以测量两个区域之间兴趣点特征的相似性。具体公式为
| $ \mathit{\boldsymbol{A}}_{ij}^{\rm{p}} = \frac{{{n_j}}}{{{N_i}}} + \log \left( {\frac{R}{{{r_j}}}} \right), $ |
式中:nj表示属于j类的兴趣点的数量;Ni表示位于网格i上的所有兴趣点的数量,通过网格总数R和包括第j个种类的兴趣点网格总数rj的商,对其取对数,来衡量网格中兴趣点的重要性。使用协方差矩阵C来计算相关系数,具体计算公式为
| $ {\mathit{\boldsymbol{C}}_{ij}} = E\left[ {\left( {{\mathit{\boldsymbol{F}}_i} - E\left( {{\mathit{\boldsymbol{F}}_i}} \right)} \right)\left( {{\mathit{\boldsymbol{F}}_j} - E\left( {{\mathit{\boldsymbol{F}}_j}} \right)} \right)} \right]。$ |
在这项工作中,采用频谱图卷积来构建城市人群流量的多种相关性的卷积算子,为了方便起见,设定图卷积算子为*
| $ {\mathit{\boldsymbol{L}}_A} = \mathit{\boldsymbol{D}}_A^{ - \frac{1}{2}}\left( {{\mathit{\boldsymbol{D}}_A} - \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{D}}_A^{ - \frac{1}{2}} = {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_A}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_A}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_A^{\rm{T}}, $ |
其中: DA∈RV×V是邻接矩阵A的度矩阵; ΨA∈RV×V和ΛA∈RV×V分别表示特征向量的矩阵形式和特征值矩阵。根据以上定义,在傅里叶域中将具有图形信号F∈RV×Z和滤波器θ∈Rk的图卷积定义为
| $ \begin{array}{c} \mathit{\boldsymbol{\theta }}*\mathbb{R}{\mathit{\boldsymbol{F}}_{:, c}} = \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \cdot \sum\limits_{k = 0}^{K - 1} {\left( {{\mathit{\boldsymbol{\theta }}_k} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^k}} \right)} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{T}}} \cdot {\mathit{\boldsymbol{F}}_{:, c}}, \\ {\mathit{\boldsymbol{H}}^{(l)}} = {\mathop{\rm ReLU}\nolimits} \left( {\mathit{\boldsymbol{\theta }}*\mathbb{R}{\mathit{\boldsymbol{F}}_{:, c}}} \right), c \in [0, Z), \end{array} $ |
式中:F: , c表示取F矩阵的第c列。ReLU为非线性激活函数,并且在每个传播层中加入参数化的注意力引导机制,注意力机制倾向于选择对于区域i影响更大的区域,对其给予更高的关联程度。对于区域i的输出为
| $ \begin{array}{l} \mathit{\boldsymbol{H}}_i^{(l + 1)} = \sum\limits_{j \in N(i) \cup \{ i\} } {\mathit{\boldsymbol{P}}_{ij}^{(l)}} \mathit{\boldsymbol{H}}_{ij}^{(l)}, \mathit{\boldsymbol{P}}_{ij}^{(l)} = \\ {\mathop{\rm softmax}\nolimits} \left( {{{\left[ {{\mathit{\boldsymbol{B}}^{(l)}}\cos \left( {\mathit{\boldsymbol{H}}_i^{(l)}, \mathit{\boldsymbol{H}}_j^{(l)}} \right)} \right]}_{j \in N(i) \cup \{ i\} }}} \right), \end{array} $ |
其中:传播矩阵Pil也是关于第l层状态和参数B(l)的函数。节点j到节点i的注意力为
| $ \mathit{\boldsymbol{P}}_{ij}^{(l)} = \left( {\frac{1}{\mathit{\boldsymbol{C}}}} \right){{\rm{e}}^{{\mathit{\boldsymbol{B}}^{(l)}}\cos \left( {{\mathit{\boldsymbol{H}}_i}, {\mathit{\boldsymbol{H}}_j}} \right)}}, \mathit{\boldsymbol{C}} = \sum\limits_{j \in N(i) \cup \{ i\} } {{{\rm{e}}^{{\mathit{\boldsymbol{B}}^{(l)}}\cos \left( {{\mathit{\boldsymbol{H}}_i}, {\mathit{\boldsymbol{H}}_j}} \right)}}} , $ |
其中:节点i到节点j在第l层的余弦距离代表了节点i到j的关联程度。
2.4 多模态融合为了更好地将人群流视图的潜在表示与相关属性融合在一起,采用基于参数矩阵的多模态融合方法,计算公式为O=W1⊙O1+W2⊙O2+W3⊙O3+W4⊙O4,其中:W1,…,W4是多模态中的区域可调参数,分别代表各种相关效应的程度;O1,…,O4表示基于注意力机制的图卷积神经网络的输出值;⊙表示向量内积。为了更好地适应突发性情况,使用基于门控机制的多模态融合:sigmoid(Oext)⊙O,Oext表示额外特征如天气、节假日等;最终的人群流量预测最终输出为:Ft=f(O+sigmoid(Oext)⊙O)。
使用Huber函数作为损失函数,
| $ \begin{array}{l} \mathit{Loss}(\mathit{\boldsymbol{\hat F}}, \mathit{\boldsymbol{F}}) = \\ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}{{(\mathit{\boldsymbol{\hat F}} - \mathit{\boldsymbol{F}})}^2}, }&{|\mathit{\boldsymbol{\hat F}} - \mathit{\boldsymbol{F}}| > T{h_{\rm{L}}}, }\\ {T{h_{\rm{L}}}|\mathit{\boldsymbol{\hat F}} - \mathit{\boldsymbol{F}}| - \frac{1}{2}Th_{\rm{L}}^2, }&{{\rm{其他, }}} \end{array}} \right. \end{array} $ |
其中:ThL表示用于限制损失函数大小的阈值(默认为1)。假设W是基于注意力神经网络的训练参数,则可以转化为优化问题:
| $ \arg \mathop {\min }\limits_W \sum\limits_{t \in T} {\sum\limits_{i = 1}^N {\sum\limits_{c = 1}^C {\mathit{Loss}} } } \left( {{\mathit{\boldsymbol{F}}^t}[i, c], {{\mathit{\boldsymbol{\hat F}}}^t}[i, c]} \right){\rm{, }} $ |
Ft[i, c]代表从第i行到第c列的流量。
3 实验与分析本文对于基于多模态融合的人群流量预测模型(MFCFP)进行了广泛的实验研究,并与五种预测算法进行对比。在两个不同的数据集分别进行了两组实验,评估所提出的MFCFP算法的有效性和参数敏感性,同时还测量了使用不同的相关图进行空间依赖建模的效果。
3.1 数据集本文使用两个不同的上海市人群流量数据集,详细信息如下。
摩拜单车:真实的摩拜单车数据包括2018年2月—2019年3月由173 202辆共享自行车在上海产生的754 327 310条行驶记录。每条记录均包括车辆ID、上车和下车时间、经纬度信息等。
出租车:出租车的真实GPS轨迹数据集,时间段为2016年6月—2016年7月。每条记录包括出租车ID、时间、经纬度等信息。区域划分和图构造方法与摩拜单车数据集设置相同。
3.2 实验设置本文将提出的MFCFP算法与其他五种人群流量预测算法进行了对比,同时还选择没有经过多模态融合的结果进行对比。其他预测算法介绍如下。
历史平均数(historical average,HA):直接使用过去一段时间的平均人群流量作为预测。
向量自回归[11](vector auto regression,VAR):是自回归模型在多元上的一个扩展版本,可以对区域之间的相关性进行建模。
梯度提升回归树(gradient boosting regression tree,GBRT):梯度提升回归树由Python的sklearn软件包实现。最佳参数是通过网格搜索自动获得的。
基于注意力机制的图卷积神经网络(attention-based graph convolutional network,AGCN):构建了一个三层图卷积神经网络,其中输入是前六个时间步长的流量,而输出是接下来的六个时间步长的流量。
扩散卷积递归神经网络(DCRNN)[8]:扩散卷积递归神经网络使用道路网络建立非欧几里得的区域关系,并通过将图卷积集成到门控循环单元中来建模时空依赖性。
评估标准:为了评估人群流量预测,使用均方根误差(RMSE) 和平均绝对误差(MAE)。目前,这两个指标已被广泛用于回归任务中。给定预测值
| $ \begin{array}{l} MAE = \frac{1}{{|T|}}\sum\limits_{t \in T} {\frac{{\sum\limits_{i, j = 1}^V {\left| {\mathit{\boldsymbol{\hat F}}_{i, j}^{(t)} - \mathit{\boldsymbol{F}}_{i, j}^{(t)}} \right|} }}{{{V^2}}}} , \\ RMSE = \sqrt {\frac{1}{{|T|}}\sum\limits_{t \in T} {\frac{{\sum\limits_{i, j = 1}^V {{{\left| {\mathit{\boldsymbol{\hat F}}_{i, j}^{(t)} - \mathit{\boldsymbol{F}}_{i, j}^{(t)}} \right|}^2}} }}{{{V^2}}}} , } \end{array} $ |
其中:T是预测的时间片段数量,预测未来T个时间片段的人群流量;
表 1显示了在不同算法下两个数据集的人群活动流量预测的误差值。其中本文算法MFCFP在所有测试中均表现最佳,已用黑体标出。与仅使用单个相关图的AGCN相比,MFCFP使用模态融合,因为MFCFP算法可以更好地补充区域之间的相关性,补充信息更加充分,因此误差通常低于AGCN。此外,在这些测试中,AGCN、DCRNN和MFCFP的效果要优于其他指标,这表明捕获城市人群活动预测的时空依赖性具有重要意义,并且可以更好地执行人群活动预测。MFCFP比DCRNN更好,主要是因为AGCN和MFCFP模型使用市区之间的相关性作为补充信息来更好地提取城市的时空依赖性,而DCRNN使用的信息相对较少。GBRT作为决策树集成模型,在摩拜单车数据集上表现良好,甚至优于VAR,但在出租车数据集上表现较差。这可能是由于其数据集的效率更高,并且GBRT很难解决出租车的高度稀疏性,因此这个数据集无法满足该方法的性能要求。
|
|
表 1 不同算法下人群活动流量预测的误差值 Tab. 1 Errors of crowd activity flow prediction under different algorithms |
为了研究多模态融合的效果,使用单个相关图来预测摩拜单车数据集的人群活动流量,将时间步长设置为6,相关图分别是区域间距离图、流量交互性图、流量相似性图和区域特征相似性图(表 2)。如表 2中黑体所示,MFCFP模型总是比仅使用单个相关性的其他图更好,这表明所提取的区域之间的相关性是有效的,并且这些空间相关性可以更好地进行人群流量预测,因此它们包括有意义的先验知识。仅使用单个相关图的模型具有相似的结果,并且使用区域兴趣点,相似关系的模型误差要小于使用其他相关图的模型,这可能是由于人群地区之间的活动主要影响因素是区域兴趣点的特征。城市中的人流往往是出于对某些特征兴趣点感兴趣,例如购物中心、电影院等,这意味着区域之间的特征兴趣点对于预测偏远人群的流向更为重要。
|
|
表 2 多个相关图的误差值 Tab. 2 The value of MAE in multiple correlation graphs |
本文提出了一种多模态融合人群流量预测模型MFCFP。该模型由基于注意力机制的图的卷积神经网络组成,用于预测城市不规则区域的流入和流出。MFCFP不仅利用城市间距离的相关性,而且还利用流量相似性、流量交互性以及区域特征相似性来更好地捕获时间和多个空间相关性。最后,使用上海市两个不同的真实数据集评估了MFCFP模型。实验结果表明,本文所提出的MFCFP方法可以很好地预测人群活动的流量。
| [1] |
LIU J M, SUN L L, LI Q, et al. Functional zone based hierarchical demand prediction for bike system expansion[C]//Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM Press, 2017: 957-966.
(  0) 0) |
| [2] |
肖立志, 张争. 基于递归卷积神经网络的行人检测方法[J]. 信阳师范学院学报(自然科学版), 2021, 34(4): 655-660. XIAO L Z, ZHANG Z. Pedestrian detection method based on recurrent convolutional neural networks[J]. Journal of Xinyang normal university (natural science edition), 2021, 34(4): 655-660. DOI:10.3969/j.issn.1003-0972.2021.04.025 (  0) 0) |
| [3] |
黄宗超, 王思为, 祝恩, 等. 基于子空间融合的多视图聚类算法[J]. 郑州大学学报(理学版), 2021, 53(1): 68-73. HUANG Z C, WANG S W, ZHU E, et al. Multi-view clustering algorithm based on subspace fusion[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(1): 68-73. (  0) 0) |
| [4] |
ASIF M T, DAUWELS J, GOH C Y, et al. Spatiotemporal patterns in large-scale traffic speed prediction[J]. IEEE transactions on intelligent transportation systems, 2014, 15(2): 794-804. DOI:10.1109/TITS.2013.2290285 (  0) 0) |
| [5] |
CHEN L B, ZHANG D Q, WANG L Y, et al. Dynamic cluster-based over-demand prediction in bike sharing systems[C]//Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing. New York: ACM Press, 2016: 841-852.
(  0) 0) |
| [6] |
KWON J, VARAIYA P. Effectiveness of California's high occupancy vehicle (HOV) system[J]. Transportation research part C: emerging technologies, 2008, 16(1): 98-115. DOI:10.1016/j.trc.2007.06.008 (  0) 0) |
| [7] |
BRUNA J, ZAREMBA W, SZLAM A, et al. Spectral networks and locally connected networks on graphs[C]//International Conference on Learning Representations. San Diego: ICLR Press, 2014: 1-14.
(  0) 0) |
| [8] |
CHAI D, WANG L Y, YANG Q. Bike flow prediction with multi-graph convolutional networks[C]//Proceedings of the 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM Press, 2018: 397-400.
(  0) 0) |
| [9] |
LI Y G, YU R, SHAHABI C, et al. Diffusion convolutional recurrent neural network: data-driven traffic forecasting[C]//International Conference on Learning Representations. San Diego: ICLR Press, 2018: 1-16.
(  0) 0) |
| [10] |
SUN J K, ZHANG J B, LI Q F, et al. Predicting citywide crowd flows in irregular regions using multi-view graph convolutional networks[EB/OL]. (2020-07-13)[2021-01-10]. DOI: 10.1109/TKDE.2020.3081717.
(  0) 0) |
| [11] |
KUMAR S V, VANAJAKSHI L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data[J]. European transport research review, 2015, 7(3): 1-9. (  0) 0) |
 2022, Vol. 54
2022, Vol. 54


