2. 长安大学 机械工程学院 陕西 西安 710061
2. School of Engineering Machinery, Chang′an University, Xi′an 710061, China
近年来,无人作战飞行器(uninhabited combat aerial vehicle, UCAV)在偏远、危险环境下出色完成复杂任务的能力受到世界各国军事组织的高度关注[1]。航迹规划是无人机飞行任务研究的核心,是指在特定的任务环境(已探知的静态威胁)下,从起点到终点寻找一条最优或次优的航迹路径。目前越来越多的智能优化算法已被应用于求解航迹规划问题,如蚁群算法、乌贼算法、粒子群算法和遗传算法等[2-5]。与上述算法相比,人工蜂群算法(artificial bee colony, ABC)[6]可以在一次迭代中同时兼顾全局搜索能力和局部搜索能力, 求得局部最优解的概率更大。此外,ABC算法具有参数少、精度高和结构简单易实现等优点,越来越多的学者将改进的人工蜂群算法应用于无人机的航迹规划问题中。文献[7]提出了基于混沌理论的改进人工蜂群算法,并应用于无人机的航迹规划;文献[8]提出了平衡进化策略的人工蜂群算法,并应用于无人机的航迹规划;文献[9]将差分进化算法融合到侦查蜂阶段,提出了改进的人工蜂群算法并应用于无人机的航迹规划;文献[10]提出了自适应搜索策略的人工蜂群算法,并应用于无人机的航迹规划;文献[11]引入动态评价策略、模拟退火准则和复合形法优化算法结构,提出了改进的人工蜂群算法并应用于无人机的航迹规划。
虽然以上改进算法都提高了无人机航迹规划问题的收敛速度,但仍存在不完善的地方。首先,种群的搜索机制仅利用一个搜索公式随机产生新的航迹,导致解的多样性不足,不利于求得潜在最优航迹;其次,在搜索过程中仅利用先前航迹信息产生候选航迹, 这种搜索机制利于勘探, 但不利于开发;最后,以上改进算法在跳脱局部最优航迹的能力方面没有得到根本的改善,导致产生的航迹存在落入威胁区内的风险,无人机避障能力未能很好实现。为解决这些问题,本文在搜索阶段中利用两种不同的搜索公式得到两组初始航迹,比较适应度值最优者作为候选航迹,增加解的多样性。同时,在搜索策略中加入个体双重认知能力和权重因子,平衡算法的勘探和开发能力,加快无人机航迹规划问题的收敛速度。最后,加入禁忌搜索策略,帮助算法跳脱局部最优航迹,避免航迹落入到威胁区内。通过5个基准函数测试验证了本文算法在求解精度、收敛速度和跳脱局部最优解等方面的有效性,同时在不同威胁区域下进行航迹规划仿真,本文算法求解的航迹具有距离更短、航迹更平滑、更好地规避威胁等优点,加快了求解航迹的收敛速度,提高了航迹规划效率和稳定性。尤其是随着威胁区域复杂度的提高,本文算法求解航迹精度的效果越显著。
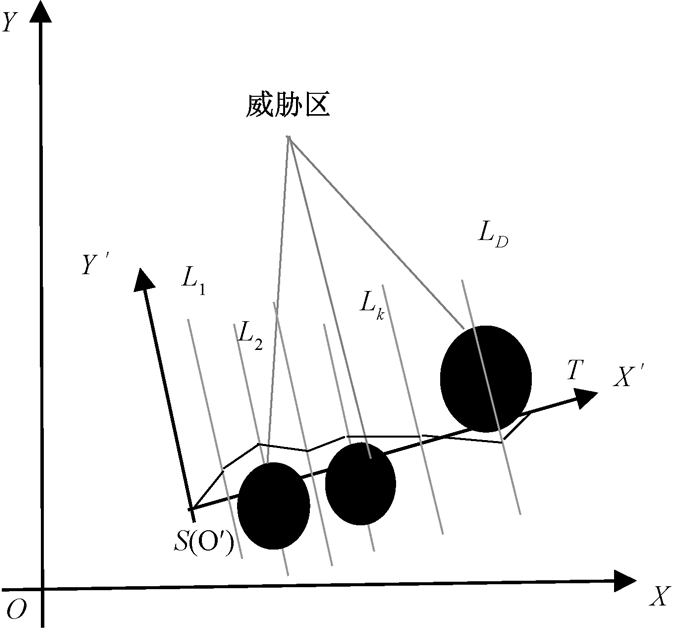
1 无人机航迹规划模型建立 1.1 无人机飞行环境模型无人机航迹规划是指在特定的威胁区域下,从起点位置和终点位置之间规划出一条航迹距离最短且尽量避开所有威胁的航迹路径。如图 1所示,无人机的飞行起点为S,终点为T,威胁区域(如雷达、导弹和防空炮等)通过圆来表示,航迹路径可以通过{S, L1(x(1), y(1)), L2(x(2), y(2)), …, LD(x(D), y(D)), T}表示。
|
图 1 航迹规划模型 Fig. 1 Route planning model |
为便于计算航迹路径,将S点作为新的坐标原点O′,直线ST作为X′轴,将过新原点O′且垂直于X′轴的直线作为Y′轴,从而得到新的坐标系O′X′Y′,新旧坐标的关系转换为
| $ \left( {\begin{array}{*{20}{c}} {x'\left( k \right)}\\ {y'\left( k \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \;\theta }&{\sin \;\theta }\\ { - \sin \;\theta }&{\cos \;\theta } \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {x\left( k \right) - {x_S}}\\ {y\left( k \right) - {y_S}} \end{array}} \right), $ |
式中:θ为直线ST与X轴之间的夹角。
将直线ST等分成D+1段,过每个等分节点作直线ST的垂线Lk,并在每条垂线Lk上取一个点,依次连接D+2个点,则上述航迹路径可以简化为D维函数优化问题,变量范围为{y′(1), y′(2), …, y′(D)}。
1.2 无人机航迹评价函数无人机的航迹评价函数由威胁代价函数和油耗代价函数共同组成[8],
| $ J = \lambda \cdot {J_{{\rm{threat}}}} + \left( {1 - \lambda } \right) \cdot {J_{{\rm{fuel}}}}, {J_{{\rm{threat}}}} = \int_0^{length} {{w_{{\rm{threat}}}}} {\rm{d}}l, {J_{{\rm{fuel}}}}\int_0^{length} {{w_{{\rm{fuel}}}}{\rm{d}}l} , $ |
式中:J为航迹总评价函数;Jthreat为航迹的威胁代价函数;Jfuel为航迹的油耗代价函数;length为总航迹长度;wthreat为路径上的威胁代价;wfuel为路径的油耗代价。λ∈(0, 1),权衡航迹的威胁代价与油耗代价之间的关系,即当λ趋于0时,要求无人机航迹距离最短且尽量避免威胁,重视航迹规划的快速性;当λ趋于1时,要求无人机牺牲航迹距离保证无人机不落入威胁区域,重视航迹规划的安全性。一般λ取值为0.5。
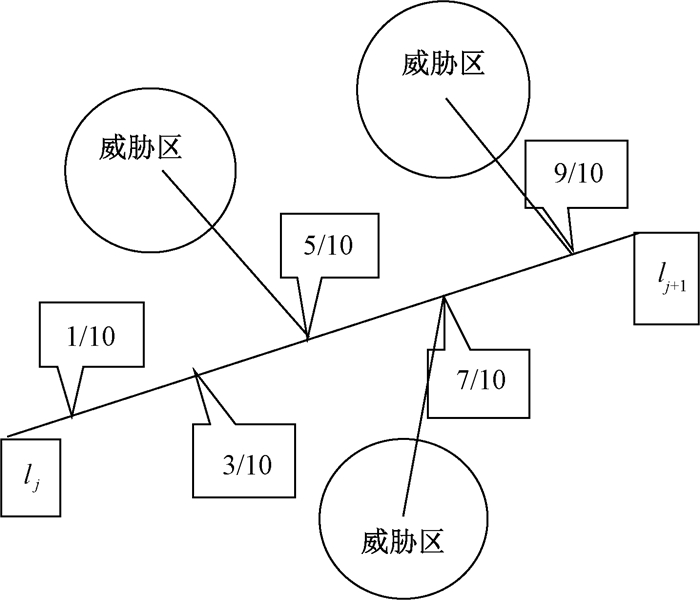
如图 2所示,为简化wthreat的计算,将相邻的两个航迹点之间的距离均分为10段,分别取该段路径的5个分点来计算子航迹的威胁代价,若威胁区域中心到该点的距离小于威胁半径,则威胁代价为
| $ {w_{{\rm{threat}}, {l_j} \to {l_{j + 1}}}} = \frac{{lengt{h_{j + 1}}}}{5}\sum\limits_{k = 1}^N {\left[ {{t_k}\left( {\frac{1}{{d_{0.1, j + 1, k}^4}} + \frac{1}{{d_{0.3, j + 1, k}^4}} + \frac{1}{{d_{0.5, j + 1, k}^4}} + \frac{1}{{d_{0.7, j + 1, k}^4}} + \frac{1}{{d_{0.9, j + 1, k}^4}}} \right)} \right]} , $ |
|
图 2 第j+1段子路径的威胁代价模型 Fig. 2 The threat cost model of the j+1 subpath |
式中:lengthj+1为第j+1段的航迹距离;N为任务区域内的所有威胁区域的个数;tk为威胁区域的等级;d0.1, j+1, k为第j+1段的子航迹1/10处到各个威胁区域中心的距离。
假设无人机匀速飞行,故无人机的油耗代价与飞行距离成正比,即简单地认为每段子路径的油耗代价wfuel, lj→lj+1=1, j∈1, 2, …,D,航迹中的油耗代价函数与航迹总长有关。
2 改进的人工蜂群算法 2.1 基于改进的局部搜索策略为平衡勘探和开发能力,本文在搜索过程中加入个体的自我认知能力和社会认知能力。自我认知能力指个体对其自身经验的认知,代表算法的勘探能力;社会认知能力指个体向种群中其他已有经验的个体学习,代表算法的开发能力。同时,加入权重因子w,提出了新的搜索公式
| $ {v_{ij}} = w{x_{ij}} + {c_1}R\left( {{x_{{\rm{best}}}} - {x_{ij}}} \right) + {c_2}R\left( {{x_{kj}} - {x_{ij}}} \right), $ | (1) |
| $ w = {w_{\max }} - \frac{{iter}}{{Maxcycle}}\left( {{w_{\max }} - {w_{\min }}} \right), $ | (2) |
式中:w为权重因子;c1和c2为学习因子,取值为2时可以获得较好的实验结果;R是[-1, 1]的随机数;xbest表示当前种群中最优解;wmax和wmin分别为权重因子的最大值和最小值,通常wmax=1.0,wmin=0.5可以获得较好的实验结果;iter表示当前迭代次数;Maxcycle表示最大的迭代次数。算法初期阶段应侧重于勘探能力,此时权重因子取较大值;随着迭代次数的增加,算法后期阶段应侧重于开发能力,此时权重因子取较小值。公式(1)的第二项为社会认知能力,通过最优解指导邻域搜索行为,以增强算法的开发能力; 公式(1)的第三项为自我认知能力,通过个体向外或向内延伸拓宽个体的搜索方向,以增强算法的勘探能力。
本文为增加解的多样性,将文献[12]提出的增强人工蜂群算法(enhancing artificial bee colony algorithm,EABC)作为本文算法的第二个搜索公式,
| $ {v_{ij}} = {x_{ij}} + \alpha \left( {{x_{{\rm{best}}}} - {x_{{r_1}j}}} \right) + \beta \left( {{x_{{r_1}j}} - {x_{{r_2}j}}} \right), $ | (3) |
式中:xbest表示当前种群中最优解;α是[0,A]均匀分布的随机数,A为任意正整数;β=N(0.3, 0.3)×rand(0, 1),N(0.3, 0.3)表示均值和方差都为0.3的随机数。
2.2 禁忌搜索策略帮助算法跳脱局部最优解途径有:爬山法、进化计算、变结构邻域搜索、禁忌搜索(Tabu search,TS)策略[13]等。其中,禁忌搜索策略具有算理清晰、易于编程实现和避免迂回搜索等优点,是一个用来跳脱局部最优解的搜索方法。其主要思想是标记已经得到的局部最优解,并在以后的迭代中避开已标记的局部最优解。本文在侦察蜂阶段加入禁忌搜索策略,雇佣蜂陷入局部最优解时,该处食物源被放弃,侦察蜂寻找新解,帮助被束缚的个体跳脱局部最优解;与此同时,采用禁忌表记录局部最优解的位置,侦察蜂产生的新解与禁忌表中的元素比对。若新解存在于禁忌表中,则需要再次进行局部搜索得到新解;否则, 算法继续。通过加入禁忌搜索策略,避免算法陷入局部最优解导致的算法早熟。
3 面向航迹规划的改进人工蜂群算法实现本文算法应用于航迹规划的主要步骤如下。
Step1 在D维空间中随机生成SN个初始航迹;
Step2 雇佣蜂在初始航迹的附近利用两种不同的搜索公式(1)、(3)进行局部搜索;
Step3 计算解的目标函数与适应度值,贪婪选择适应度值较优的航迹路线;
Step4 全部的雇佣蜂完成一次局部搜索,侦察蜂利用轮盘赌算子计算概率Pi选择航迹路线,并在该航迹的附近搜索,寻找新的航迹,贪婪选择较优的航迹路线;
Step5 如果航迹的收益率没有通过预先确定的循环次数得到改善时,算法陷入局部最优解时,使用禁忌表存储其位置。该航迹路线被放弃,与之对应的雇佣蜂转化为侦察蜂。侦察蜂随机产生新解并与禁忌表中的元素比对,若新解存在于禁忌表中,重新产生新解;
Step6 若迭代次数小于最大迭代次数,转至Step2;否则,输出最优航迹,算法结束。
4 性能验证为测试本文算法的性能,选取5个基准函数[14]分别对ABC算法、EABC算法以及本文算法进行测试。在50维情况下独立运行50次,并统计各算法的最优值、最差值、平均值和标准差。实验结果如表 1和表 2所示。其中,平均值反映了算法的求解精度;标准差反映了算法的稳定性。算法参数设置如下:种群规模设置为100;阈值为300;最大的迭代次数为200;维数为50。
|
|
表 1 各算法在50维情况下对单峰基准函数测试的实验结果 Tab. 1 Experimental results of uni-modal functions tested by each algorithm in 50 dimensions |
|
|
表 2 各算法在50维情况下对多峰函数测试的实验结果 Tab. 2 Experimental results of multi-modal functions tested by each algorithm in 50 dimensions |
表 1中的数据表明,ABC算法的稳定性差,收敛精度不高。通过分析表中函数的实验结果可以得出,本文算法的最优值和最差值与ABC算法、EABC算法相比都有明显的提高。同时,本文算法的平均值和标准差都优于另外两种算法。因此说明,在收敛速度和精度方面,本文算法优于ABC算法,可以有效提高算法的局部搜索能力;表 2中的数据表明,ABC算法容易陷入局部最优值。通过分析表中实验结果可以得出,本文算法的最优值和最差值与ABC算法、EABC算法相比都有明显的提高。同时,本文算法的平均值和标准差都优于另外两种算法。因此说明,在算法的整体寻优和跳脱局部最优值方面,本文算法优于ABC算法。
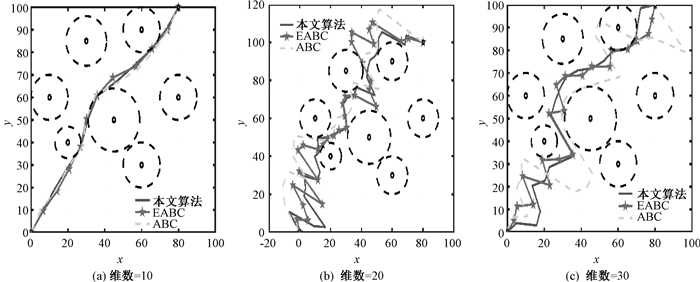
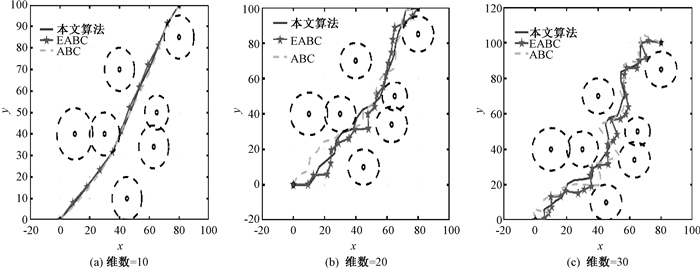
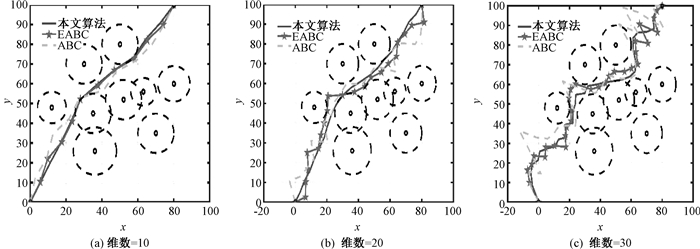
5 航迹规划仿真本文在3个不同威胁区域下进行无人机航迹规划仿真实验(表 3),实验参数设置如下:种群规模设置为60;阈值为50;最大的迭代次数为100;维数分别为10、20及30,仿真结果如图 3~图 5所示。
|
|
表 3 无人机威胁区域环境设置 Tab. 3 Environmental settings for UAV threat area |
|
图 3 威胁区域1下航迹规划结果对比图 Fig. 3 Comparison of route planning results under threat area 1 |
|
图 4 威胁区域2下航迹规划结果对比图 Fig. 4 Comparison of route planning results under threat area 2 |
|
图 5 威胁区域3下航迹规划结果对比图 Fig. 5 Comparison of route planning results under threat area 3 |
从航迹规划结果对比图可以得出,与ABC算法、EABC算法相比,本文算法求得的航迹路线更平滑,航迹规划性能最佳。从图 3(c)中可以发现,ABC算法、EABC算法陷入局部最优解,即航迹路线落入威胁区内,而本文算法有效改善陷入局部最优解的问题。
为了进一步验证本文算法的优越性,表 4给出了三种算法进行航迹规划的航迹距离。以威胁区域2为例,可以看出,当维数为20时ABC算法的航迹距离为172.673 0,EABC算法的航迹距离为146.031 2,本文算法的航迹距离为134.430 7,规划效率分别提高了22.15%和7.94%,这说明本文算法求得航迹路线更短。另一方面,对比不同威胁区域下的统计结果,可以发现本文算法在维数越多、威胁越复杂时寻优效果越显著。
|
|
表 4 各算法分别在维数为10、20及30情况下对三种威胁区域的航迹规划距离 Tab. 4 Each algorithm plans the distance of the trajectory in three threat areas in 10, 20 and 30 dimensions respectively |
| [1] |
孙健, 井立, 刘朝君. 突发威胁下的无人机航迹规划算法[J]. 飞行力学, 2018, 36(3): 52-55. SUN J, JING L, LIU Z J. Route planning algorithm of UAV with unexpected threat[J]. Flight dynamics, 2018, 36(3): 52-55. (  0) 0) |
| [2] |
陈侠, 艾宇迪, 梁红利. 基于改进蚁群算法的无人机三维航迹规划研究[J]. 战术导弹技术, 2019(2): 59-66. CHEN X, AI Y D, LIANG H L. Research on three-dimensional path planning of UAV based on improved ant colony algorithm[J]. Tactical missile technology, 2019(2): 59-66. (  0) 0) |
| [3] |
钱洲元, 雷明. 面向无人机航迹规划的自适应乌贼算法[J]. 哈尔滨工业大学学报, 2019, 51(10): 37-46. QIAN Z Y, LEI M. Adaptive cuttlefish algorithm for UAV path planning[J]. Journal of Harbin institute of technology, 2019, 51(10): 37-46. (  0) 0) |
| [4] |
杜云, 刘冰, 邵士凯, 等. 基于改进粒子群算法的无人机航迹规划[J]. 河北工业科技, 2019, 36(5): 335-340. DU Y, LIU B, SHAO S K, et al. UAV flight path planning based on improved particle swarm optimization[J]. Hebei journal of industrial science & technology, 2019, 36(5): 335-340. (  0) 0) |
| [5] |
李楠, 张建华. 基于改进遗传算法的无人机航路规划[J]. 计算机仿真, 2016, 33(4): 91-94. LI N, ZHANG J H. Path planning for unmanned aerial vehicles based on improved genetic algorithm[J]. Computer simulation, 2016, 33(4): 91-94. DOI:10.3969/j.issn.1006-9348.2016.04.021 (  0) 0) |
| [6] |
KARABOGA D, AKAY B. A comparative study of artificial bee colony algorithm[J]. Applied mathematics and computation, 2009, 214(1): 108-132. DOI:10.1016/j.amc.2009.03.090 (  0) 0) |
| [7] |
XU C F, DUAN H B, LIU F. Chaotic artificial bee colony approach to uninhabited combat air vehicle (UCAV) path planning[J]. Aerospace science and technology, 2010, 14(8): 535-541. DOI:10.1016/j.ast.2010.04.008 (  0) 0) |
| [8] |
LI B, GONG L G, YANG W L. An improved artificial bee colony algorithm based on balance-evolution strategy for unmanned combat aerial vehicle path planning[J]. The scientific world journal, 2014, 2014: 232704. (  0) 0) |
| [9] |
徐流沙, 吴梅, 袁志敏. 改进人工蜂群算法的无人机航迹规划研究[J]. 火力与指挥控制, 2015, 40(1): 62-66. XU L S, WU M, YUAN Z M. Research on path planning of UAV based on improved ABC algorithm[J]. Fire control & command control, 2015, 40(1): 62-66. (  0) 0) |
| [10] |
于霜, 丁力, 吴洪涛. 基于改进人工蜂群算法的无人机的航迹规划[J]. 电光与控制, 2017, 24(1): 19-23. YU S, DING L, WU H T. Path planning for UAVs based on improved artificial bee colony algorithm[J]. Electronics optics & control, 2017, 24(1): 19-23. (  0) 0) |
| [11] |
王庆海. 基于改进人工蜂群算法的无人机航迹规划技术研究[D]. 郑州: 郑州大学, 2018. WANG Q H. Research on techniques of UAV path planning based on improved artificial bee colony algorithm[D]. Zhengzhou: Zhengzhou University, 2018. (  0) 0) |
| [12] |
GAO W F, LIU S Y, HUANG L L. Enhancing artificial bee colony algorithm using more information-based search equations[J]. Information sciences, 2014, 270: 112-133. DOI:10.1016/j.ins.2014.02.104 (  0) 0) |
| [13] |
GLOVER F, TAILLARD E, TAILLARD E. A users guide to Tabu search[J]. Annals of operations research, 1993, 41(1): 1-28. (  0) 0) |
| [14] |
GAO W F, LIU S Y. Improved artificial bee colony algorithm for global optimization[J]. Information processing letters, 2011, 111(17): 871-882. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


