2. 中原工学院 电子信息学院 河南 郑州 451191;
3. 郑州大学 电气工程学院 河南 郑州 450001
2. School of Electronics and Information Engineering, Zhongyuan University of Technology, Zhengzhou 451191, China;
3. School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China
图像边缘处理是目标识别的基础步骤,得到边缘的清晰程度直接影响目标检测的成功率,因此边缘检测问题一直是图像处理领域的研究热点之一,带噪声图像的边缘检测目前仍面临巨大的挑战.
常见的边缘检测算子包括Sobel算子[1]、Prewitt算子[2]等.基于微分的边缘提取算法的基本思想是辨别局部最大值或一阶偏导和二阶偏导的零交叉点,这些算法虽然运算简单,但对噪声较为敏感.另外,阈值的选择问题对边缘检测的结果影响很大,如何选择最优阈值是这些算法面临的主要问题之一.随着数学工具与人工智能算法的发展,一些新处理工具的引进,如小波变换[3-4]、曲线演化[5]和磁滞技术[6],在某种程度上提高了边缘检测的性能.因为高频噪声污染点也是局部最大点或者一阶偏导和二阶偏导的零交叉点,因此,传统的边缘检测算法在处理高频污染图像时往往失效,不能得到清晰的边缘图像.
为解决高频污染图像的边缘提取及阈值选择问题,本文提出一种基于SCC[7]的边缘检测新算法.图像是由光滑点和边缘点组合而成,因此本文创新性地将图像边缘检测问题转换为二值分类问题,即变为仿射子空间混合的图像平滑点和边缘点的分类问题.由于平滑点和边缘点的信息无法标记,因此该二分类问题只能通过无监督学习算法完成.常见的无监督学习算法往往依托于各类聚类算法,通过估计每一个平面的相关参数以及与其相关的数据点之间的分布特点,如K-均值聚类算法[8],C-均值聚类算法[9].然而上述算法在有噪声点的情形下,聚类性能受到很大影响,而SCC有望解决该情形下的分类问题.特别地,当噪声点位于平滑点和边缘点以外的子空间中,SCC能够有效处理噪声数据.
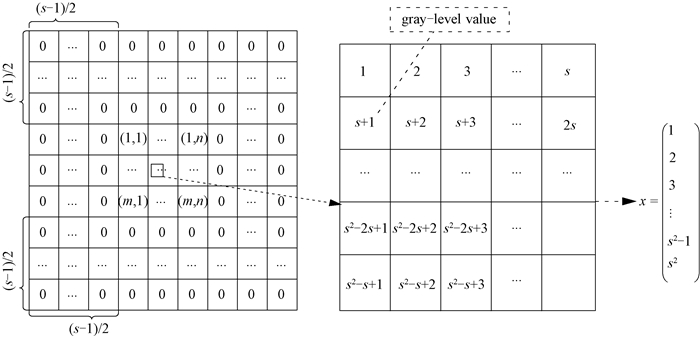
1 系统模型 1.1 数据集构建一个像素的空域特征信息取决于它的邻域.因此,在一幅灰度图像中,将一个s×s大小的窗口(可以转换为s2×1的矢量)视为数据集X中一个样本点.特别地,位于第一行或第一列的灰度值并没有较多的邻域.为解决该问题,将该灰度矩阵(m×n)扩展到(m+s-1, n+s-1),其前(s-1)/2和后(s-1)/2行和列均填充零,为了更好地说明这一过程,示意图如图 1所示.
|
图 1 数据集构造过程 Figure 1 The process of data construction |
通过将所有的数据点按列的形式进行排列,即可得数据集X=[x1, …, xN].接下来讨论中,我们认为数据集中的每一列即为该簇中的一个数据点.
1.2 相似矩阵的构造通过利用数据点的相似信息,可以将数据集分为两部分.不同于获取每个数据点的局部信息,我们通过捕获仿射子空间中数据点集合的曲率多模相似性,来避免处理子空间交叉区域点的复杂操作.每个顶点的极正弦[10]可以表示为psinzi(z1, …, zd+2)=(d+1)!Vd+1(z1, …, zd+2)/
相似矩阵可以构造为W=A·A′.由此,可以计算出数据集X中数据点的相似度,位于相同子空间的数据点的相似度大于子空间互异数据点的相似度.因此,两个数据点的相似度越大,两个点越有可能位于相同的类中.为对所提聚类算法进行评估,采用文献[7]中的平均正交最小二乘估计误差eOLS.
1.3 算法流程对本文所提算法的主要步骤描述如下:
1) 初始化.对于待检测图像,通过1.1中方法构造数据集X,数据点的维度为d(1≤d≤s2),且样本子空间的分类平面K=2,采样列数为c(默认为100).
2) 聚类.使用文献[7]中SCC算法对数据集X进行处理.
3) 二值化.C1中聚类的样本数据灰度值根据它的位置设定为1.同样,C2中的数据点灰度值设为0,定义该二值图像为A.
4) 称β(A)为A的边缘数据集,且β(A)=A-(AΘB),其中B为正确的边缘点集合,(AΘB)表示B对A的腐蚀.
1.4 复杂度分析所提算法的复杂度主要来源于SCC算法.假设ns表示每个样本点的迭代次数,那么SCC总的运行时间数量级为O(ns·(d+1)2·m·n·c).
2 仿真结果为验证所提算法的有效性,分别在图像‘cameraman’和BSDS500数据集[11]上进行了实验.因为s为所提算法的关键参数,我们分别研究了当s=3, 5, 7, 9和d≤9时,所提算法在‘cameraman’图 2(a)和受到椒盐噪声污染‘cameraman’图 2(b)上的效果,结果分别对应于图 2中的(c),(d),(e),(f).

|
图 2 参数s对去噪效果的影响 Figure 2 The influence of parameter s on denoising |
通过图 2可以得出如下结论:首先,噪声得到了很好的抑制和消除.原因是如果数据集中的一个向量无论在边缘组还是在平滑组中都明显增加了eOLS,那么就判断该点为噪声点,并在接下来的采样过程中忽略它.正因为噪声点位于不同于边缘点和光滑点的子空间中,所以大部分的噪声点可以被成功消除.因此,不难理解参数s为什么能够影响一个具体的边缘信息.从视觉效果看,虽然s=5, 7, 9时,算法性能差别不大,但均比s=3时效果要好.然而,就几何边缘形状提取效果而言,s=3, 5, 7, 9的效果差别并不是很显著.因此,在接下来的实验中,本文设定s=3,但不难理解所提算法性能将随着s的增加而增加.最后,维度d的选择也不必过大,一方面,我们发现采用d≤9和采用更大的d时对于提高算法性能的影响很小.另一方面,较小的d有助于降低算法的运算复杂度.
第二组实验包括4幅图,编号分别为37 073, 81 066, 100 007, 368 037,它们中的一个表示为图片形式,其他结果用表格的形式对检测比和错误比[12]进行归纳,其分别定义为:Pd=Nright/Nedge,Pf=Nwrong/Nedge,其中:Nedge为参考图像的边缘点个数;Nright代表正确检测的边缘点个数;Nwrong代表被错误检测为边缘点的非边缘点个数.图 3显示了编号为37 073的实验结果.从视觉效果来看,所提算法明显优于canny算子.为阐述数值结果,表 1呈现了与多个算法的对比分析结果.在这些对比试验中,假设所有的图像都是经过椒盐噪声的污染.

|
图 3 不同边缘检测算法效果对比图 Figure 3 Comparison of performance for different algorithms |
|
|
表 1 BSDS500图像的仿真结果 Table 1 Experimental results for BSDS500 images |
由于在聚类过程中移除了大量的噪声点,所提算法的的错误检测概率明显低于其他算法,换言之,准确概率显著提高.
3 结论本文提出一种新的算法,通过分类能够有效提取数值图像的边缘特征信息.相比于传统算法,特别针对噪声图像,仿真结果表明检测概率能够达到0.95左右,而且通过设计合适的s和d值可以进一步提高检测概率.但是,如何从理论上确定合适参数d是下一步考虑的主要工作.
| [1] |
GAO W, ZHANG X, YANG L, et al. An improved Sobel edge detection[C]// Proceedings of IEEE International Conference on Computer Science and Information Technology. Chengdu, 2010: 67-71.
(  0) 0) |
| [2] |
CHAPLE G N, DARUWALA R D, GOFANE M S. Comparisons of robert, prewitt, sobel operator based edge detection methods for real time uses on FPGA[C]// Proceedings of IEEE International Conference on Technologies for Sustainable Development. Mumbai, 2015: 1-4.
(  0) 0) |
| [3] |
LI W S, ZHAO J. Application of wavelet transform in edge detection[C]// Proceeding of IEEE International Congress on Image and Signal Processing. Shanghai, 2011: 2173-2176.
(  0) 0) |
| [4] |
JIANG W, LAM K M, SHEN T Z. Efficient edge detection using simplified Gabor wavelets[J]. IEEE transactions on systems man and cybernetics part B, 2009, 39(4): 1036-1047. DOI:10.1109/TSMCB.2008.2011646 (  0) 0) |
| [5] |
XU C, PRINCE J L. Snakes, shapes, and gradient vector flow[J]. IEEE transactions on image processing, 1998, 7(3): 359-369. DOI:10.1109/83.661186 (  0) 0) |
| [6] |
MEDINA-CARNICER R, CARMONA-POYATO A, MUÑOZ-SALINAS R, et al. Determining hysteresis thresholds for edge detection by combining the advantages and disadvantages of thresholding methods[J]. IEEE transactions on image processing, 2010, 19(1): 165-173. DOI:10.1109/TIP.2009.2032942 (  0) 0) |
| [7] |
CHEN G, LERMAN G. Spectral curvature clustering (SCC)[J]. International journal of computer vision, 2009, 81(3): 317-330. DOI:10.1007/s11263-008-0178-9 (  0) 0) |
| [8] |
曾庆山, 张贵勇. 基于距离阈值的自适应K-均值聚类算法[J]. 郑州大学学报(理学版), 2016, 48(4): 90-94. (  0) 0) |
| [9] |
刘洪普, 杨乐, 侯向丹, 等. 一种改进的模糊C均值图像分割算法[J]. 郑州大学学报(理学版), 2017, 49(2): 66-71. (  0) 0) |
| [10] |
CHEN G, LERMAN G. Foundations of a multi-way spectral clustering framework for hybrid linear modeling[J]. Foundations of computational mathematics, 2009, 9(5): 517-558. DOI:10.1007/s10208-009-9043-7 (  0) 0) |
| [11] |
MARTIN D R, FOWLKES C C, MALIK J. Learning to detect natural image boundaries using local brightness, color, and texture cues[J]. IEEE transactions on pattern analysis and machine intelligence, 2004, 26(5): 530-549. DOI:10.1109/TPAMI.2004.1273918 (  0) 0) |
| [12] |
WANG Q Z, WANG K, YUAN G L, et al. Multi-hierarchy and adaptive space coefficient image edge detection based on Gauss wavelet[J]. Journal of image and graphics, 2009, 27(9): 1347-1353. (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


