2. 广东理工学院 信息工程系 广东 肇庆 526100
2. Department of Information Engineering, Guangdong Polytechnic College, Zhaoqing 526100, China
聚类是数据分析的基础,目前已经提出了许多聚类算法,这些算法可以分为单视角聚类算法和多视角聚类算法两类.如K-means、基于谱函数的聚类算法、基于密度的聚类算法等都是单视角聚类算法[1-2],而在实际的生活中,数据的表示可以有多种形式,例如一个文本可以用多种语言表示,一张图片可以用文字、颜色和形状等来表示.依据数据多方面的特征对数据进行聚类的方法称为多视角聚类.和单视角聚类算法相比,多视角聚类具有聚类精度高的优势[3-6].
聚类算法的收敛性是基于迭代技术的聚类算法的基础.文献[7]利用反例理论证明了模糊聚类算法(FCM)的收敛性;文献[8]利用Zangwill定理证明了PCA(possibilistic clustering algorithms)算法的收敛性,指出该算法产生迭代序列收敛或至少存在一个子序列收敛于PCA聚类目标函数的局部极小值点或鞍点;文献[9]讨论了多目标演化算法的收敛性问题;文献[10-12]分别研究了均值漂移、极大熵聚类、谱聚类等聚类算法的收敛性.这些收敛性证明都是针对单视角聚类算法,而多视角聚类算法MVKKM[13]将多特征样本点的不同视角映射到对应的高维特征空间,在特征空间内通过算法核K-means完成聚类.多视角聚类算法还没有理论证明算法的收敛性.针对这一问题,借鉴现有的单视角聚类算法收敛性证明方法,考虑通过迭代法优化其目标函数,而Zangwill定理是证明迭代算法收敛性的一个有效工具,本文使用Zangwill收敛性定理证明了多视角MVKKM的收敛性.
1 多视角核K-means算法的收敛性 1.1 多视角核定义1 令χ={x1(v), x2(v), …, xN(v)}v=1V表示一个非空集合,其中xi(v)∈Rd(v)(1≤i≤N).函数K(v):x(v)×x(v)→R,当且仅当K(v)是对称的,即K(xi(v), xj(v))=K(xj(v), xi(v)), 并且满足方程
| $\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{c_i}{c_j}\mathit{\boldsymbol{K}}\left( {\mathit{\boldsymbol{x}}_i^{\left( v \right)},\mathit{\boldsymbol{x}}_j^{\left( v \right)}} \right) \ge 0,N \ge 2,} } $ |
其中:cr∈R,r=1, 2, …, N,v=1, 2, …,K(v)称为多视角正定核.
对任意多视角正定核都存在映射
| $\varphi :\chi \to H,\mathit{\boldsymbol{K}}\left( {\mathit{\boldsymbol{x}}_i^{\left( v \right)},\mathit{\boldsymbol{x}}_j^{\left( v \right)}} \right) = {\left\langle {\varphi \left( {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{j}}^{\left( v \right)}} \right),\varphi \left( {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\left( v \right)}} \right)} \right\rangle _{{H^{\left( v \right)}}}},$ |
其中H(v)表示多视角的特征空间.
定义2 若矩阵
假设数据集χ={x1(v), x2(v), …, xN(v)}v=1V⊂Rs,φ(v):x(v)→φ(x(v))∈H(v)是从数据集χ到特征空间H的映射,K(v)是映射φ(v)对应的核函数.结合多核思想,多视角核K-means算法(MVKKM)的聚类模型可以描述为下面的优化问题:
| ${J_H}\left( {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{w}},\mathit{\boldsymbol{u}}} \right) = \mathop {\min }\limits_{\left\{ {{\mathit{\boldsymbol{z}}_v}} \right\}_{v = 1}^V} \sum\limits_{v = 1}^V {\mathit{\boldsymbol{z}}_v^p} \sum\limits_{i = 1}^N {\sum\limits_{k = 1}^C {{\delta _{ik}}{{\left\| {{\varphi ^{\left( v \right)}}\left( {\mathit{\boldsymbol{x}}_i^{\left( v \right)}} \right) - \mathit{\boldsymbol{w}}_k^{\left( v \right)}} \right\|}^2},} } $ | (1) |
其中:V是视角的个数, N为数据个数, p是多视角权重系数,C是聚类数目,z如式(2) 所示是多视角的权重,uik如式(3)~(5) 所示,表示多视角数据集的硬0≤zv≤1划分,wk(v)表示特征空间中第v视角的第k类的中心,
| $\sum\limits_{v = 1}^V {{\mathit{\boldsymbol{z}}_v} = 1,0} \le {\mathit{\boldsymbol{z}}_v} \le 1,$ | (2) |
| ${\mathit{\boldsymbol{u}}_{ik}} \in \left\{ {0,1} \right\},1 \le k \le C,1 \le i \le N,$ | (3) |
| $\sum\limits_{k = 1}^C {{\mathit{\boldsymbol{u}}_{ik}} = 1,} 1 \le i \le N,$ | (4) |
| $\sum\limits_{i = 1}^N {{\mathit{\boldsymbol{u}}_{ik}} > 0,} 1 \le k \le C.$ | (5) |
所有多视角数据集的硬k划分集合用Mk表示:
| ${M_k} = \left\{ {\mathit{\boldsymbol{u}} \in {{\bf{R}}^{CN}}\left| {\mathit{\boldsymbol{u}}\;满足式\;\left( 3 \right) \sim \left( 5 \right)} \right.} \right\}.$ | (6) |
所有多视角权重集合用Mfc表示:
| ${M_{fc}} = \left\{ {\mathit{\boldsymbol{z}}\left| {\mathit{\boldsymbol{z}} \in {{\bf{R}}^v};\mathit{\boldsymbol{z}}\;满足式\;\left( 2 \right)} \right.} \right\},$ | (7) |
| ${Q_v} = \sum\limits_{i = 1}^N {\sum\limits_{k = 1}^C {{\mathit{\boldsymbol{u}}_{ik}}{{\left\| {{\varphi ^{\left( v \right)}}\left( {\mathit{\boldsymbol{x}}_i^{\left( v \right)}} \right) - \mathit{\boldsymbol{w}}_k^{\left( v \right)}} \right\|}^2}.} } $ | (8) |
由式(1) 目标函数的最优化,得到式(9)~(11) 的迭代式,其中:(z(v)*, w(v)*, u*)是JH局部最小值, 多视角聚类中心迭代:
| ${\left( {\mathit{\boldsymbol{w}}_k^{\left( v \right)}} \right)^ * } = \sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_{ik}^ * {\varphi ^{\left( v \right)}}\left( {\mathit{\boldsymbol{x}}_i^{\left( v \right)}} \right)} /\sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_{ik}^ * } ,\;\;\;\;1 \le k \le C,1 \le v \le V.$ | (9) |
多视角权重迭代:
| $\mathit{\boldsymbol{z}}_v^ * = 1/\sum\limits_{v' = 1}^V {{{\left( {\frac{{Q_v^ * }}{{Q_{v'}^ * }}} \right)}^{\frac{1}{{p - 1}}}}} ,p > 1,1 \le v \le V.$ | (10) |
多视角数据集的硬k划分迭代:
| $\mathit{\boldsymbol{u}}_{ik}^ * = 1,k \in \left\{ {r \in Q\left| {r = \arg \mathop {\min }\limits_{1 \le l \le C} {d_{li}}} \right.} \right\},1 \le k \le C,1 \le i \le N.$ | (11) |
其中:
定义3 若T:Y→P(Z),则称映射T是从集合Y到集合Z的点到集映射.其中P(Z)表示Z的幂集,即T把Y中的每个点映射为Z的一个子集.
定义4[14] 设Y和p(z)分别是空间Rp和Rq中的非空闭集,T:Y→P(Z)为点到集的映射.如果{y(k)}⊂Y, y(k)→y, z(k)∈T(y(k)), z(k)→z,蕴含z∈T(y),则称映射T在z(v)=(z1, z2, …, zv)处是闭的.
定理1 (Zangwill收敛性定理)[15-16]设V是距离空间,点z(1)∈V, T:V→P(V)是V上点到集合的映射,由T定义的算法以z(1)为初始点产生的序列{z(k)}k=1, 2, …,令Ω⊂V表示解集,如果:
1) 所有的点z(k)都属于V中的一个紧子集.
2) 存在连续函数J:V→R,使得:
① 若z∉Ω,对任何y∈T(z),有J(y)<J(z);
② 若z∈Ω,则或算法终止,或对任何y∈T(z),有J(y)≤J(z).
3) 若z∉Ω,则映射T在z点是闭的.
满足上述条件则算法停止于某个解上,或任何一个收敛子序列的极限是一个解.
定义函数G1:Mfc×Mk→Hcv:
| ${G_1}\left( {{\mathit{\boldsymbol{z}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right) = {\mathit{\boldsymbol{w}}^{\left( v \right)}} = {\left( {\mathit{\boldsymbol{w}}_1^{\left( v \right)},\mathit{\boldsymbol{w}}_2^{\left( v \right)}, \cdots ,\mathit{\boldsymbol{w}}_k^{\left( v \right)}} \right)^{\rm{T}}},$ | (12) |
式中:wk(v)=(wk(1), wk(2), …, wk(v))T∈Hcv,向量通过式(9) 定义,1≤k≤C,1≤v≤V.定义函数G2:Hcv×Mk→Mfc:
| ${G_2}\left( {{\mathit{\boldsymbol{w}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right) = {\mathit{\boldsymbol{z}}^{\left( v \right)}} = {\left( {{\mathit{\boldsymbol{z}}_1},{\mathit{\boldsymbol{z}}_2}, \cdots ,{\mathit{\boldsymbol{z}}_v}} \right)^{\rm{T}}},$ | (13) |
向量z(v)=(z1, z2, …, zv),1≤v≤V,由式(10) 定义.定义点到集的映射G3:Mfc×Hcv→P(Mk),
| ${G_3}:{M_{fc}} \times {H^{cv}} \to P\left( {{M_k}} \right):{G_3}\left( {{\mathit{\boldsymbol{z}}^{\left( v \right)}},{\mathit{\boldsymbol{w}}^{\left( v \right)}}} \right) = \left\{ {\mathit{\boldsymbol{u}} \in {\mathit{\boldsymbol{M}}_k}\left| {\mathit{\boldsymbol{u}}\;满足等式\left( {11} \right)} \right.} \right\},$ | (14) |
式中1≤v≤V.
MVKKM算法的迭代序列可以用点到集的映射T:Mfc×Hcv×Mk→P(Mfc×Hcv×Mk)表示,其定义的映射为T=A3οA2οA1,其中:
| ${A_1}:{M_{fc}} \times {H^{cv}} \times {M_k} \to {H^{cv}} \times {M_k},{A_1}\left( {{\mathit{\boldsymbol{z}}^{\left( v \right)}},{\mathit{\boldsymbol{w}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right) = \left( {{G_1}\left( {{\mathit{\boldsymbol{z}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right),\mathit{\boldsymbol{u}}} \right),$ | (15) |
| ${A_2}:{H^{cv}} \times {M_k} \to {M_{fc}} \times {H^{cv}},{A_2}\left( {{\mathit{\boldsymbol{w}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right) = \left( {{G_2}\left( {{\mathit{\boldsymbol{w}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right),{\mathit{\boldsymbol{w}}^{\left( v \right)}}} \right),$ | (16) |
| ${A_3}:{M_{fc}} \times {H^{cv}} \to P\left( {{M_{fc}} \times {H^{cv}} \times {M_k}} \right),{A_3}\left( {{\mathit{\boldsymbol{z}}^{\left( v \right)}},{\mathit{\boldsymbol{w}}^{\left( v \right)}}} \right) = \\ \left\{ {\left( {{\mathit{\boldsymbol{z}}^{\left( v \right)}},{\mathit{\boldsymbol{w}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right)\left| {\mathit{\boldsymbol{u}} \in {G_3}\left( {{\mathit{\boldsymbol{z}}^{\left( v \right)}},{\mathit{\boldsymbol{w}}^{\left( v \right)}}} \right)} \right.} \right\}.$ | (17) |
综上可知,
定义5 若(z(1)(v), w(1)(v), u(1))∈Mfc×Hcv×Mk,(z(v), w(k)(v), u(k))∈T(z(k-1)(v), w(k-1)(v), u(k-1)),其中k=2, 3,…, 则称{(z(k)(v), w(k)(v), u(k))}是MVKKM算法的迭代序列.
引理1 令Ξ:Mk→R由Ξ(u)=JH(w(v)*, z(v)*, u)定义,其中:w(v)*∈Hcv,z*∈Mfc,对任意p>1,则Ξ关于u在Mk上所有全局极小值点构成的集合恰是由方程(11) 所确定的关于u的集合.
证明 充分性:如果u∈Mk满足式(11),对于1≤v≤V时,JH是最小的.
必要性:如果JH对于1≤v≤V是最小的,得到
引理2 令Θ:Mfc→R定义为Θ(z(v))=JH(z(v), w(v)*, u*),其中:w(v)*∈Hcv,u*∈Mk,对任意p>1,则z(v)为Θ在Mk上全局最小的值,等价于z(v),满足式(10).
证明 当p>1时,函数Θ(zv)是严格的凸函数,上述问题是一个凸优化问题.引入Lagrange乘子,
| $L = \sum\limits_{v = 1}^V {\mathit{\boldsymbol{z}}_v^p{Q_v}} + \lambda \left( {\sum\limits_{v = 1}^V {{\mathit{\boldsymbol{z}}_v} - 1} } \right),$ |
当Qv>0时,式(1) 的最优解等价于式(18)、(19) 的解:
| $\partial L/\partial {\mathit{\boldsymbol{z}}^{\left( v \right)}} = 0,1 \le v \le V,$ | (18) |
| $\partial L/\partial \lambda = 0.$ | (19) |
式(18)、(19) 等价变换化简可得式(10), 又由式(10) 易见,它也是加强约束条件优化问题:min Θ(z(v)),z(v)∈Mfc的唯一全局最优解.
引理3 令Ψ:Hcv→R由Ψ(w(v))=JH(z(v)*, w(v), u*)定义,其中:u*∈Mk, z(v)*∈Mfc,对于任意p>1,如果w(v)满足式(9),那么w(v)是Ψ在Hcv的全局最小值.
证明 因为Ψ(w(v))是关于w(v)的严格凸函数,它取全局唯一极小值的充要条件是满足式(9), 即得证.
定理2 设χ={x1(v), x2(v), …,xN(v)}v=1V,1≤v≤V,权重系数p>1,若χ至少包含C(C<N)个不同的点,则Ω满足min JH的解为:
| $\begin{align} & \quad \Omega =\left\{ \left( {{{\mathit{\boldsymbol{\bar{z}}}}}^{\left( v \right)}},{{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar{u}}} \right)\in {{M}_{fc}}\times {{H}^{cv}}\times {{M}_{k}}\left| {{J}_{H}}\left( {{{\mathit{\boldsymbol{\bar{z}}}}}^{\left( v \right)}},{{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar{u}}} \right)\le {{J}_{H}}\left( {{{\mathit{\boldsymbol{\bar{z}}}}}^{\left( v \right)}},{{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar{u}}} \right) \right. \right. \\ & \forall \mathit{\boldsymbol{u}}\in {{M}_{k}}, \\ & {{J}_{H}}\left( {{{\mathit{\boldsymbol{\bar{z}}}}}^{\left( v \right)}},{{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar{u}}} \right)<{{J}_{H}}\left( {{{\mathit{\boldsymbol{\bar{z}}}}}^{\left( v \right)}},{{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar{u}}} \right)\forall {{\mathit{\boldsymbol{w}}}^{\left( v \right)}}\ne {{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},{{J}_{H}}\left( {{{\mathit{\boldsymbol{\bar{z}}}}}^{\left( v \right)}},{{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar{u}}} \right) \\ & \left. <{{J}_{H}}\left( {{\mathit{\boldsymbol{z}}}^{\left( v \right)}},{{{\mathit{\boldsymbol{\bar{w}}}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar{u}}} \right)\forall {{\mathit{\boldsymbol{z}}}^{\left( v \right)}}\ne {{{\mathit{\boldsymbol{\bar{z}}}}}^{\left( v \right)}} \right\}. \\ \end{align}$ | (20) |
设(z(v), w(v), u)∈Mfc×Hcv×Mk,任意给定p>1,则
证明 由
| ${J_H}\left( {{{\mathit{\boldsymbol{\hat z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\hat u}}} \right) \le {J_H}\left( {{{\mathit{\boldsymbol{\hat z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) \le {J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}},} \right) \le {J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right).$ | (21) |
式(21) 蕴含着
下面证明当(z(v), w(v), u)∉Ω时,
| ${J_H}\left( {{{\mathit{\boldsymbol{\hat z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\hat u}}} \right) = {J_H}\left( {{{\mathit{\boldsymbol{\hat z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) = {J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}},} \right) = {J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right).$ | (22) |
由引理3可知,
| ${J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) > {J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},{\mathit{\boldsymbol{u}}^ * }} \right),{\mathit{\boldsymbol{u}}^ * } \in {M_k},$ | (23) |
| ${J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) \ge {J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},\mathit{\boldsymbol{w}}_{\left( v \right)}^ * ,\mathit{\boldsymbol{\bar u}}} \right),\mathit{\boldsymbol{w}}_{\left( v \right)}^ * \ne {{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},$ | (24) |
| ${J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) \ge {J_H}\left( {\mathit{\boldsymbol{z}}_{\left( v \right)}^ * ,{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right),\mathit{\boldsymbol{z}}_{\left( v \right)}^ * \ne {{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}}.$ | (25) |
在式(23) 中,因为JH(z(v), w(v), u)>JH(z(v), w(v), u*),由
在式(24) 中,因为JH(z(v), w(v), u)≥JH(z(v), w(v)*, u),由
同理在式(25) 中,因为
| ${J_H}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) \ge {J_H}\left( {\mathit{\boldsymbol{\bar z}}_{\left( v \right)}^*,{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) = {J_H}\left( {\mathit{\boldsymbol{\bar z}}_{\left( v \right)}^*,{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) > {J_H}\left( {{{\mathit{\boldsymbol{\hat z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\bar u}}} \right) = \\ {J_H}\left( {{{\mathit{\boldsymbol{\hat z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\hat w}}}^{\left( v \right)}},\mathit{\boldsymbol{\hat u}}} \right),$ | (26) |
式(26) 和假设相矛盾.
引理4 给定多视角数据集χ={x1(v), x2(v), …, xN(v)}v=1V, 1≤v≤V,设χ至少包含C(C<N)个不同点,任意给定权重系数p>1,则式(15) 定义的映射A1(z(v), w(v), u)=(G1(z(v), u), u)在Mfc×Hcv×Mk是连续的.
证明 由A1的定义知A1(z(v), w(v), u)=(G1(z(v), u), u),G1=(G11, G12,…, Gkv):Mfc×Mk→Hcv,其中
引理5 给定多视角数据集χ={x1(v), x2(v), …, xN(v)}v=1V,1≤v≤V,设χ至少包含C(C<N)个不同点,任意给定权重系数p>1,则由式(16) 定义的映射A2(w(v), u)=(G2(w(v), u), w(v))在Hcv×Mk是连续的.
证明 由A2定义知,A2(w(v), u)=(G2(w(v), u), w(v)), G2是根据式(10) 计算得到,
| $F\left( {{\mathit{\boldsymbol{w}}^{\left( v \right)}},\mathit{\boldsymbol{u}}} \right) = 1/\sum\limits_{v' = 1}^V {{{\left( {\frac{{{Q_v}}}{{{Q_{v'}}}}} \right)}^{\frac{1}{{p - 1}}}}} ,$ | (27) |
式中:
推论1[16] C:M→V是一个函数, T:V→P(V)是点到集的映射.如果C在w0点是连续的且T在C(w0)是闭的, 那么点到集的映射TοC:M→P(V)在w0处是闭的.
引理6 设χ至少包含C(C<N)个不同点,任意给定系数p>1,则定义在式(17) 的映射A3:Mfc×Hcv→P(Mfc×Hcv×Mk)在Mfc×Hcv×Mk是闭的.
证明 因为A3={(z(v), w(v), u)∈Mfc×Hcv×Mk|u∈G3(z(v), w(v))},要证明G3是一个点到集的闭映射, 设
| $\left( {\mathit{\boldsymbol{z}}_{\left( v \right)}^{\left( r \right)},\mathit{\boldsymbol{w}}_{\left( v \right)}^{\left( r \right)}} \right) \to \left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}}} \right),r = 1,2,k,$ | (28) |
| ${\mathit{\boldsymbol{u}}^{\left( r \right)}} \in {G_3}\left( {\mathit{\boldsymbol{z}}_{\left( v \right)}^{\left( r \right)},\mathit{\boldsymbol{w}}_{\left( v \right)}^{\left( r \right)}} \right),r = 1,2,k,$ | (29) |
| ${\mathit{\boldsymbol{u}}^{\left( r \right)}} \to \mathit{\boldsymbol{\bar u}},r = 1,2,k,$ | (30) |
假设式(28)~(30) 成立,则只需证明u∈G3(z(v), w(v)).
设
| ${I_{ki}}\left( {\mathit{\boldsymbol{z}}_{\left( v \right)}^{\left( r \right)},\mathit{\boldsymbol{w}}_{\left( v \right)}^{\left( r \right)}} \right) \to {I_{ki}}\left( {{{\mathit{\boldsymbol{\bar z}}}^{\left( v \right)}},{{\mathit{\boldsymbol{\bar w}}}^{\left( v \right)}}} \right),r = 1,2, \cdots .$ |
对于1≤v≤V,Iki(z(v), w(v))是有限的集合,则存在r1对于所有的r>r1,使Iki(z(v)(r), w(v)(r))=Iki(z(v), w(v)).从式(30) 映射中得到uki(r)→uki,r=1, 2, …,由于uki=1或者0,存在r2对于r>r2,uki(r)=uki.式(29) 对于k∈Iki(z(v)(r), w(v)(r)),有uki(r)=1,从式(28)~(30),对于k∈Iki(z(v), w(v)),得到uki=1,所以给出u∈G3(z(v), w(v)).
定理3 设χ至少包含C(C<N)个不同的点, 权重系数p>1,则映射T:Mfc×Hcv×Mk→P(Mfc×Hcv×Mk)在Mfc×Hcv×Mk是闭的.
证明 由引理4~6和推论1得到定理3的结论.
定理4 设χ至少包含C(C<N)个不同的点,任意给定p>1,其中(z(v)(0), w(v)(0), u(v)(0))表示T的初始迭代点,满足w(v)(0)∈Hcv,z(v)(0)∈Mfc,u(0)∈G3(z(v)(0), w(v)(0)),则迭代
(JH)(k)(z(v)(0), w(v)(0), u(0))∈Mfc×[conv(x)]C×Mk,k=1, 2,…,Mfc×[conv(χ)]C×Mk, 包含于Mfc×Hcv×Mk的紧子集中.
证明 如果z(v)(0)∈Mfk,w(v)(0)∈Hcv,那么通过式(11) 得到u(0)=G3(z(v)(0), w(v)(0))∈Mk,继续递归得到满足式(9) 的
从式(2) 和(7) 得到Mfc是闭的, 并且是有界限的,由于[conv(χ)]是有限的凸包,所以它是闭的,因此[conv(χ)]C也是闭的和有界限的.因为Mk集合是χ集合的k划分,所以Mk是闭的、有限的,因而它们都是紧的,因此Mfc×[conv(χ)]C×Mk是Mfc×Hcv×Mk的紧子集.
定理5 (MVKKM收敛定理)设χ至少包含C(C<N)个不同的数据点,权重系数p>1,初始迭代点z(0)∈Mfc,w(0)∈Hcv,u(0)∈G3(z(v)(0), w(v)(0)),则迭代序列{z(v)(t), w(v)(t), u(t)}t=1, 2, k或收敛于与解集Ω的点{z(v)(*), w(v)(*), u(*)},或至少存在一个子序列收敛在Ω上.
证明 因为MVKKM的目标函数JH(z(v), w(v), u)在Mfc×Hcv×Mk上是连续的,因此结合定理2~4,再应用Zangwill定理可得迭代序列{z(v)(t), w(v)(t), u(t)}t=1, 2, k是收敛或子序列收敛的.
2 收敛速率下面通过实验分析MVKKM算法的收敛速率.实验环境:CPU为Intel(R)Core(TM)i3-2130,3.40 GHz,内存为4 G,操作系统为32位Win7旗舰版操作系统.算法编写环境:Matlab R2010a.
MVKKM算法的收敛速率取决于很多的因素:聚类的初始值;多视角的数目v;聚类的数目C;权重的指数p的值.本文采用了两个真实的UCI数据集进行实验,其中A1和A2代表数据集A(多特征数据集)中的不同的数据,B1和B2代表数据集B(Corel数据集)中的不同数据,实验中根据不同的p值,测试实验在不同视角下的运行收敛速率,其中A为5个视角,B为7个视角.图 1是数据集A和B在不同p值下的运行速率,图 2是数据集A和B在不同p值下的迭代次数.
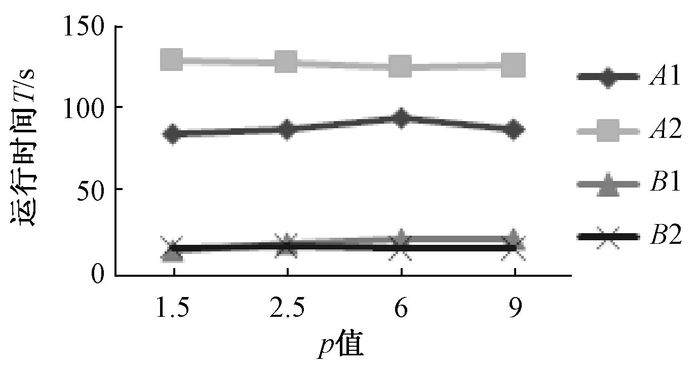
|
图 1 收敛速率 Figure 1 Rate of convergence |
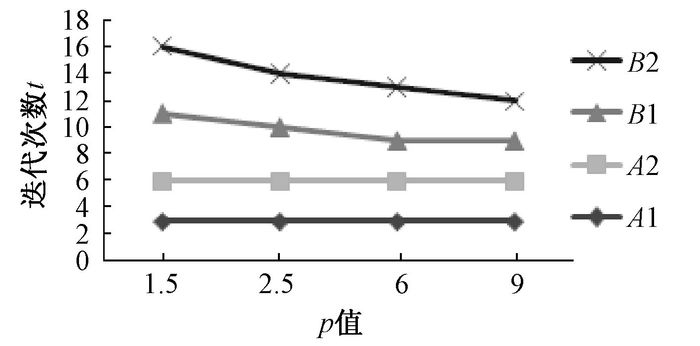
|
图 2 迭代次数 Figure 2 Iteration number |
实验的结果受数据集、参数v和p值的影响,在数据集A或者B中,相同的视角v, 不同的p, 运行速度不相同.在A1和A2中,相同的v, 运行速度不一样,迭代次数不相同.从实验中可以看到B数据集的运行速度比A数据集的快,因为B中数据的数量比A数据的小,其中B的数据量为2 800个数据,而A为4 000个数据.B数据集的迭代次数比A多,是因为B的数据结构更复杂, 视角数更大, 实验说明算法的收敛速率受不同因素的影响.
3 结束语本文利用Zangwill收敛定理证明了多视角聚类算法MVKKM的收敛性.当权重系数p>1时,且数据集χ中至少包含C(C<N)个不同的点时,MVKKM算法产生的迭代序列至少子序列收敛,并通过实验验证了该算法的收敛性.收敛性的论证可以为多视角聚类算法的基础理论研究和算法的改进提供借鉴.在收敛性论证的基础上,可以对提高多视角聚类算法的精度和收敛速率的方法进行研究.
| [1] |
李欣雨, 袁方, 刘宇, 等. 面向中文新闻话题检测的多向量文本聚类方法[J]. 郑州大学学报(理学版), 2016, 48(2): 47-52. (  0) 0) |
| [2] |
陶佰睿, 李青龙, 苗凤娟, 等. 码本聚类矢量量化算法在说话人识别中的应用[J]. 河南科技大学学报(自然科学版), 2016, 37(1): 35-39. (  0) 0) |
| [3] |
ZHAO X, EVANS N, DUGELAY J. A subspace co-training framework for multi-view clustering[J]. Pattern recognition letters, 2014, 41(1): 73-82. (  0) 0) |
| [4] |
HUSSAIN S F, MUSHTAQ M, HALIM Z. Multi-view document clustering via ensemble method[J]. Journal of intelligent information systems, 2014, 43(1): 81-99. DOI:10.1007/s10844-014-0307-6 (  0) 0) |
| [5] |
EATON E, DESJARDINS M, JACOB S. Multi-view constrained clustering with an incomplete mapping between views[J]. Knowledge & information systems, 2014, 38(1): 231-257. (  0) 0) |
| [6] |
YIN Q, WU S, HE R, et al. Multi-view clustering via pairwise sparse subspace representation[J]. Neurocomputing, 2015, 156(25): 12-21. (  0) 0) |
| [7] |
BEZDEK J C, HATHAWAY R J, SABIN M J, et al. Convergence theory for fuzzy c-means: count erexamples and repairs[J]. IEEE transactions on systems and cybernetics, 1987, 17(5): 873-877. (  0) 0) |
| [8] |
ZHOU J, CAO L, YANG N. On the convergence of some possibilistic clustering algorithms[J]. Fuzzy optimization & decision making, 2013, 12(4): 415-432. (  0) 0) |
| [9] |
周育人, 闵华清, 许孝元, 等. 多目标演化算法的收敛性研究[J]. 计算机学报, 2004, 27(10): 1415-1421. DOI:10.3321/j.issn:0254-4164.2004.10.015 (  0) 0) |
| [10] |
李乡儒, 吴福朝, 胡占义. 均值漂移算法的收敛性[J]. 软件学报, 2005, 16(3): 365-374. (  0) 0) |
| [11] |
任世军, 王亚东. 极大熵聚类算法的收敛性定理证明[J]. 中国科学:信息科学, 2010, 40(4): 583-590. (  0) 0) |
| [12] |
高炜, 周定轩. 与一般相似度函数相关的谱聚类的收敛性[J]. 中国科学:数学, 2012, 42(10): 985-994. (  0) 0) |
| [13] |
TZORTZIS G, LIKAS A. Kernel-based weighted multi-view clustering[C]//Proceedings of the IEEE 12th International Conference on Data Mining.Washington, 2012: 675-684.
(  0) 0) |
| [14] |
陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 1989, 411-432.
(  0) 0) |
| [15] |
ZANGWILL W I, MOND B. Nonlinear programming: a unified approach[M]. New Jersey: Prentice-Hall Englewood Cliffs, 1969.
(  0) 0) |
| [16] |
HATHAWAY R, BEZDEK J, TUCKER W. An improved convergence theory for the fuzzy isodata clustering algorithms[J]. Analysis of fuzzy information, 1987, 3: 123-132. (  0) 0) |
| [17] |
张志华, 郑南宁, 史罡. 极大熵聚类算法及其全局收敛性分析[J]. 中国科学:技术科学, 2001, 31(1): 59-70. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


