2. 广东石油化工学院 自动化学院 广东 茂名 525000
2. College of Automation, Guangdong University of Petrochemical Technology, Maoming 525000, China
智慧交通系统为复杂多变的交通运输、交通安全、交通管理的健康发展提供了强有力的保障。然而,由于行驶的汽车速度过快、光照条件不充分、成像距离过远、设备的分辨率较低等因素,往往导致图像在获取过程中发生退化,造成图像模糊[1],尤其是运动模糊[2]最为常见。这极大限制了交通成像和交通监控[3]等领域的发展,不仅影响正常的视觉效果,严重时甚至无法辨别所拍摄车辆的车号牌、颜色和类型等重要信息,给道路交通监督管理部门带来了巨大挑战。因此,开展道路交通模糊图像清晰化校正研究意义重大。
近些年,深度学习因其较强的学习和适应能力而得到了较好的发展,卷积神经网络逐渐被应用于图像处理领域,使图像复原的过程和结果得到了较大的突破。文献[4]提出DeblurGAN的去模糊网络,使用生成对抗的思想并结合多重损失函数的端到端学习法,去除图像上因为物体运动而产生的模糊,对于尺度较大的模糊图像,其复原细节较平滑。文献[5]设计了一个空间金字塔深堆叠的层级多补丁网络,通过从细到粗的分层对模糊图像进行逐步复原,使运动模糊图像得到了较好的清晰化校正,然而复杂类型模糊图像的复原效果通常不够理想。文献[6]提出一种全卷积去模糊网络,采用滤波变换和特征注意来实现空间自适应特征学习,在非均匀模糊数据集上能够得到视觉较好的复原结果,但在实际道路交通模糊图像上复原清晰度较差。已有的深度学习方法进行端对端图像复原在很大程度上依赖于模型的设计和目标函数的制定,复原图像的质量难以保证。
本文依据生成对抗网络理论,设计一种提取特征能力更强的优化多尺度残差块,并引入到多尺度编解码网络中作为生成对抗网络的生成器,对模糊图像进行多尺度逐级清晰化校正。在GoPro数据集和真实道路场景模糊图像上进行实验对比分析,验证了本文方法优于近些年的一些经典去模糊模型。
1 相关工作 1.1 生成对抗网络生成对抗网络[7](generative adversarial network, GAN) 总体结构包含生成器和判别器两个部分,在计算机视觉领域展现出强大的能力。在图像去模糊任务中,生成器G负责不断学习真实清晰图像的数据分布,然后将模糊图像B生成相对清晰的图像G(B),判别器D则是对送进来的图像通过判别概率值的大小进行真假鉴别,两个模型相互博弈共同学习。网络在训练的时候采取分开优化的思路,分步进行单独交替训练。生成对抗网络的基本模型如图 1所示。

|
图 1 生成对抗网络的基本模型 Fig. 1 The basic model of generative adversarial network |
在图像去模糊生成对抗网络中,目标函数通常为
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_G \;\mathop {{\rm{max}}}\limits_D \;V\left( {D, G} \right) = {E_{S\sim {P_{{{sharp}}}}(S)}}[{\rm{log}}\left( {D\left( S \right)} \right)] + \\ {E_{B\sim {P_{{{blurry}}}}(B)}}[{\rm{log}}\left( {1{\rm{ - }}D\left( {G\left( B \right)} \right)} \right)], \end{array} $ | (1) |
式中: G和D分别代表生成器和判别器; E表示期望; S~Psharp(S)表示清晰图像S取自清晰图像数据集; B~Pblurry(B)表示模糊图像B取自模糊图像数据集。
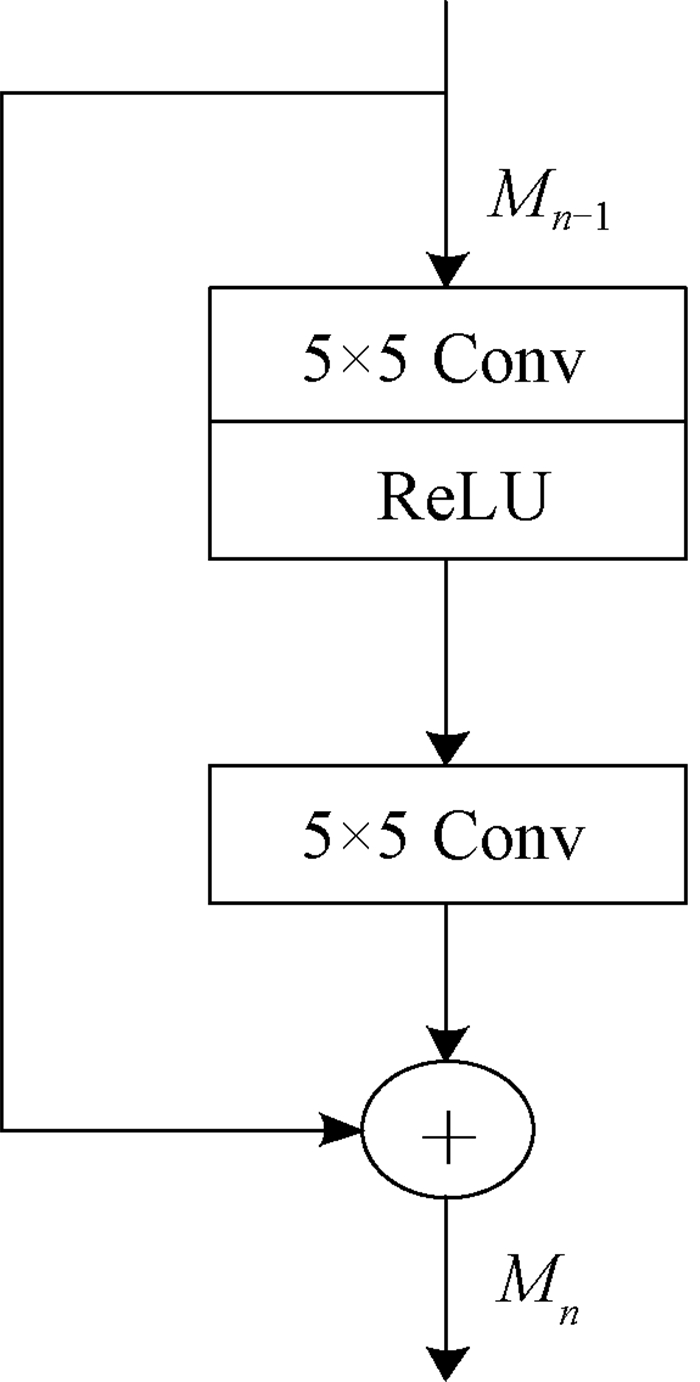
1.2 图像特征提取模块 1.2.1 残差模块相比于传统的卷积模块,残差模块Resblock[8]可以使原始输入信息直接传输到后面的层中,在图像进行特征提取过程中,不仅不增加多余的参数和计算量,而且随着网络的加深,其表达性能会越好。残差模块结构如图 2所示。
|
图 2 残差模块结构 Fig. 2 Residual module architecture |
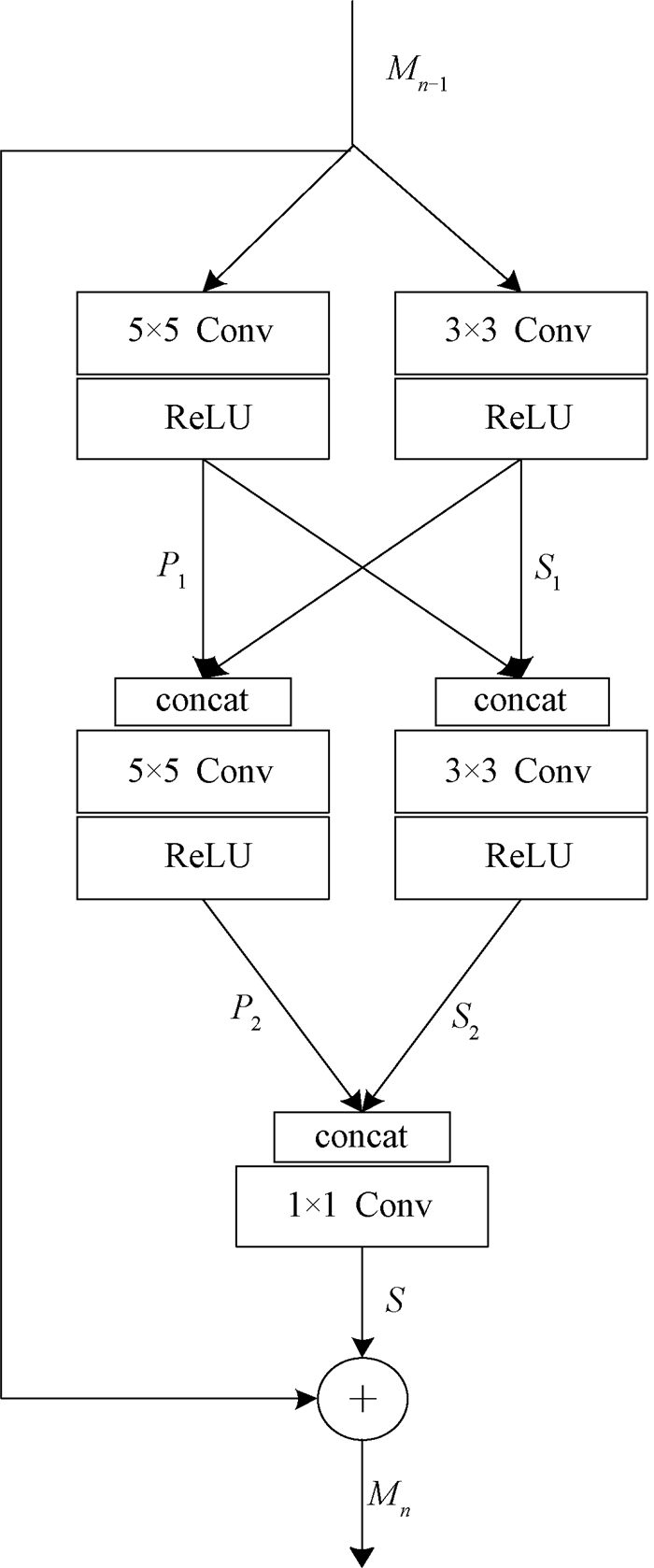
为了在不增加深度的情况下提取更多有效的特征信息,文献[9]基于多尺度特征融合和局部残差学习的思路提出多尺度残差块(multi-scale residual block,MSRB)的网络结构,使用3×3和5×5的卷积核提取不同尺度下图像的特征,然后将得到的多尺度特征进行相互拼接来共享和重复使用,多尺度残差块结构如图 3所示。
|
图 3 多尺度残差块结构 Fig. 3 Multi-scale residual block architecture |
例如,当n=1时,输入首先经过M0分成左右两个分支,左分支和右分支分别是5×5和3×3的卷积核。通过之后,将两部分的输出串接在一起,作为后部分网络的输入,此时特征图的通道数是最初的两倍。重复上述操作,得到的通道数是最初的四倍。使用残差的思想必须保持输入、输出通道数相同,因此网络在最后使用1×1的卷积核对特征通道数进行压缩,加上学习到的残差,即输出M1。
具体的计算公式为
| $ \left\{ {\begin{array}{*{20}{l}} {{S_1} = \sigma \left( {\omega _{3 \times 3}^1*{M_{n - 1}} + b_{3 \times 3}^1} \right), }\\ {{P_1} = \sigma \left( {\omega _{5 \times 5}^1*{M_{n - 1}} + b_{5 \times 5}^1} \right), }\\ {{S_2} = \sigma \left( {\omega _{3 \times 3}^2*\left[ {{S_1}, {P_1}} \right] + b_{3 \times 3}^2} \right), }\\ {{P_2} = \sigma \left( {\omega _{5 \times 5}^2*\left[ {{P_1}, {S_1}} \right] + b_{5 \times 5}^2} \right), }\\ {S = \omega _{1 \times 1}^3*\left[ {{S_2}, {P_2}} \right] + b_{1 \times 1}^3, }\\ {{M_n} = S + {M_{n - 10}}}。\end{array}} \right. $ | (2) |
多尺度残差块基于不同大小的卷积核可以得到不同尺度的图像特征为主要思想,并加入两个特征连接操作来共享和重复使用特征信息,然而左右两个分支分别经过两层5×5和3×3卷积后,通道数成倍递增,造成了参数过多且计算相对复杂等一系列问题。
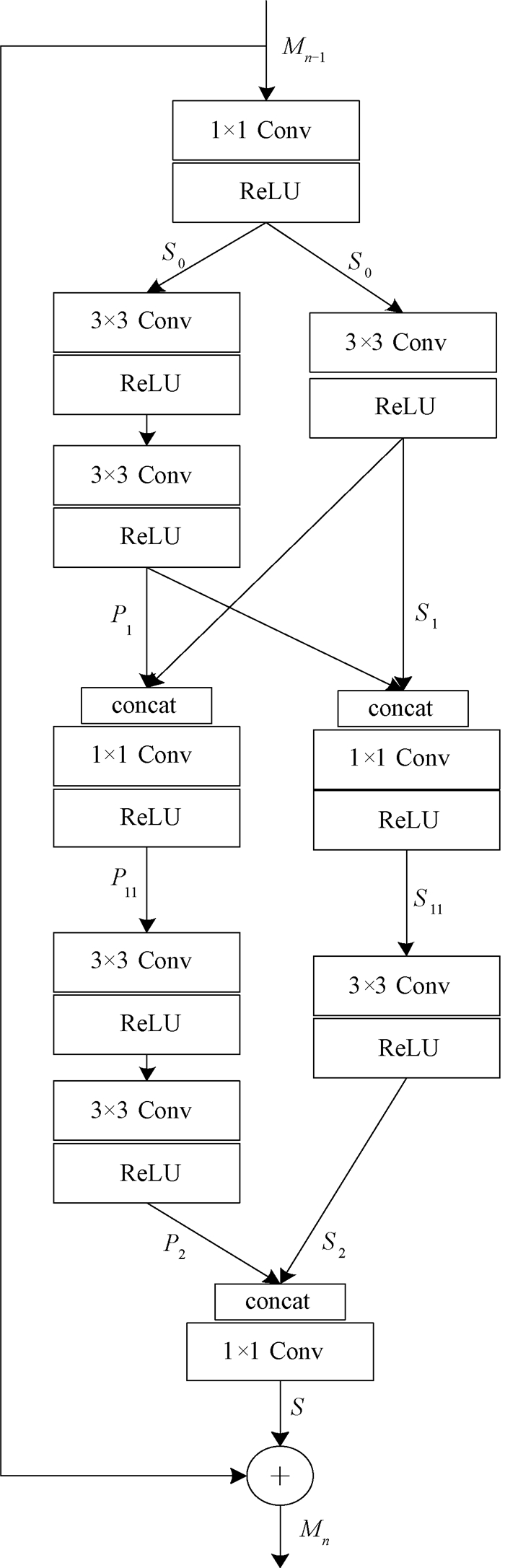
本文提出一种如图 4所示的优化多尺度残差块(optimization multi-scale residual block,OMSRB)网络结构,该结构共包含三个1×1卷积层,分别用来增加网络的深度、代替特征拼接和起到特征融合的作用。
|
图 4 优化多尺度残差块结构 Fig. 4 Architecture of optimization multi-scale residual block |
此外,使用两个3×3卷积层代替一个5×5卷积层,在得到相同感受野的情况下使计算量大幅度减小,非线性表达能力得以增强,在增加网络深度的同时,使网络对多尺度输入具有更强的适应性。
具体的计算公式为
| $ \left\{ {\begin{array}{*{20}{l}} {{S_0} = \sigma \left( {\omega _{1 \times 1}^1*{C_1} + b_{1 \times 1}^1} \right), }\\ {{S_1} = \sigma \left( {\omega _{3 \times 3}^2*{M_{n - 1}} + b_{3 \times 3}^2} \right), }\\ {{P_1} = \sigma \left[ {\omega _{3 \times 3}^{22}*\sigma \left( {\omega _{3 \times 3}^{21}*{M_{n - 1}} + b_{3 \times 3}^{21}} \right) + b_{3 \times 3}^{22}} \right], }\\ {{S_{11}} = \sigma \left( {\omega _{1 \times 1}^3*\left[ {{S_1}, {P_1}} \right] + b_{1 \times 1}^3} \right), }\\ {{P_{11}} = \sigma \left( {\omega _{1 \times 1}^3*\left[ {{P_1}, {S_1}} \right] + b_{1 \times 1}^3} \right), }\\ {{S_2} = \sigma \left( {\omega _{3 \times 3}^4*{S_{11}} + b_{3 \times 3}^4} \right), }\\ {{P_2} = \sigma \left[ {\omega _{3 \times 3}^{42}*\sigma \left( {\omega _{3 \times 3}^{41}*{P_{11}} + b_{3 \times 3}^{42}} \right) + b_{3 \times 3}^{42}} \right], }\\ {S = \omega _{1 \times 1}^5*\left[ {{S_2}, {P_2}} \right] + b_{1 \times 1}^5, }\\ {{M_n} = S + {M_{n - 1}}}。\end{array}} \right. $ | (3) |
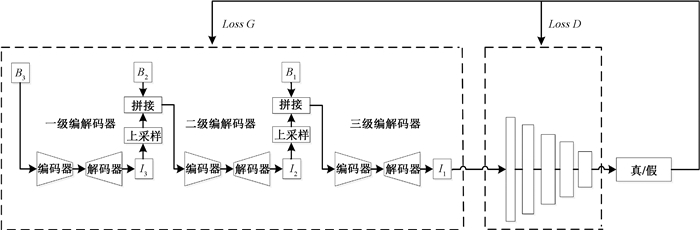
多尺度编解码深度卷积神经网络整体结构如图 5所示。每一级都是由编码器(encoder)和解码器(decoder)两个部分共同组成,从较小尺度开始逐步细化输出,网络的输入B3、B2和B1分别为64×64、128×128、256×256分辨率的模糊图像,每层的输出I3、I2和I1的分辨率也分别对应为64×64、128×128、256×256。在训练过程中,上一层网络的输出进行2倍上采样,并和下层分辨率相同的模糊图像共同作为下层网络的输入,在不同尺度上的详细定义可以表示为
| $ {I^i}({h^i}) = Ne{t_{{\rm{MS}}}}({B^i}, {I^{i + 1 \uparrow }}, {h^{i + 1 \uparrow }};{\theta _{{\rm{MS}}}}), $ | (4) |
|
图 5 多尺度编解码网络整体结构 Fig. 5 Overall architecture of multi-scale encoder-decoder network |
其中:i代表不同的网络尺度,i=1表示精尺度,i=2表示中间尺度,i=3表示粗尺度;Bi和Ii分别表示第i尺度输入的模糊图像和复原结果;NetMS代表多尺度编解码网络;θMS是训练的参数;hi表示隐层状态特征,用来获得高层图像结构和内部信息;↑表示从第i尺度调整到i+1尺度的算子。本文使用双线性插值的方法对图像进行缩放。
最终,多尺度编解码器将经过三级网络结构生成的复原图像I1送进判别器进行整体真假判断,判别结果通过反向调参反馈给生成器部分。经过多次针对性训练,使生成器生成较高质量的清晰图像。
2.2 生成器网络使用多尺度编解码作为网络的生成器模块,生成器网络结构如图 6所示。编解码器分别由三个编解码模块组合而成。每个编码模块由一个卷积层和三个优化多尺度残差块组成,该部分进行图像特征的提取,得到图像主要的内容信息进而去除模糊。每个解码模块则是与编码模块一一对称,由三个优化多尺度残差块和一个转置卷积层组成,该部分主要用来恢复图像的内容细节信息,使图像复原结果更加真实可靠。

|
图 6 生成器网络结构 Fig. 6 Generator network architecture |
由于网络结构相对较深,在训练过程中为了防止梯度消失、梯度爆炸等现象的发生,在编解码网络中每间隔一个特征提取模块就添加一条跳跃连接。该设置在提取特征的同时保留了原始图像信息,不仅可以加速网络的收敛,还有助于图像的复原。
为了进一步保证模糊图像的去除效果,在网络结构中使用ConvGRU,该模块具有更快的训练速度和相对较小的内存需求,其网络结构可以表示为
| $ {f^i} = Ne{t_{{\rm{EN}}}}({B^i}, {I^{i + 1 \uparrow }};{\theta _{{\rm{EN}}}}), $ | (5) |
| $ {h^i}({g^i}) = ConvGRU({h^{i + 1 \uparrow }}, {f^i};{\theta _{{\rm{GRU}}}}), $ | (6) |
| $ {I^i} = Ne{t_{{\rm{DE}}}}({g^i};{\theta _{{\rm{DE}}}}), $ | (7) |
其中:NetEN和NetDE分别表示带有参数θEN和θDE的编码器和解码器网络;θGRU代表ConvGRU的参数集。隐层状态hi可以获取中间结果的有用信息,该参数往往传递到较精细的尺度中,用来在下一尺度上精细化去模糊效果。
计算每层网络复原结果和相同分辨率清晰图像S3、S2和S1的L2损失,三层网络的总和作为总体的目标函数,得到的256×256分辨率下的清晰图像为最终的复原结果。
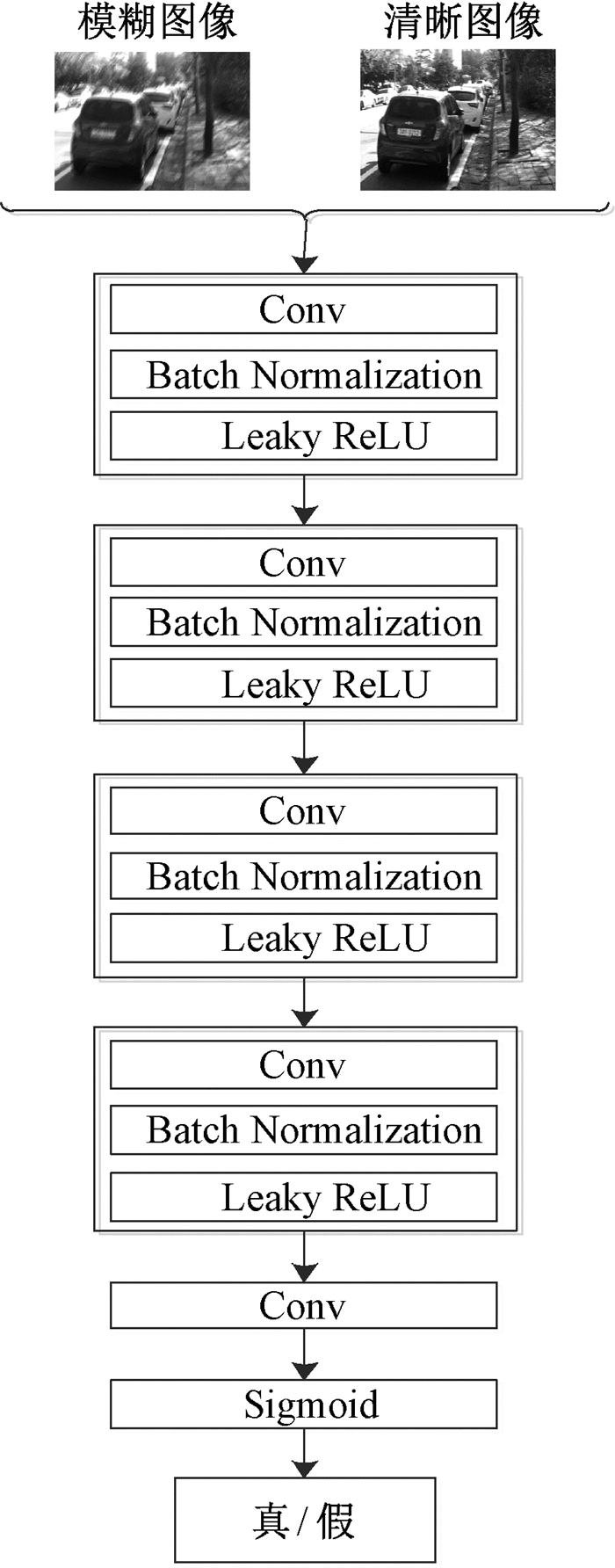
2.3 判别器网络判别器网络结构如图 7所示。使用PatchGAN[10]鉴别器进行训练,该判别器更加关注图像的局部高频细节信息,以图像块作为输入,通过N×N大小的滑动窗口遍历整张图像,每个图像块经PatchGAN输出判别为真的概率值,最后所有输出值取平均来获得整张图像的真实性概率。判别器参数设置见表 1。
|
图 7 判别器网络结构 Fig. 7 Discriminator network architecture |
|
|
表 1 判别器参数 Tab. 1 Discriminator parameter |
判别器网络前四个卷积块分别由卷积层、批规范化层和斜率为0.2的Leaky ReLU激活函数组成,最后一层使用Sigmoid激活函数产生0~1之间的值来判别样本的真伪。取N=60,这样的设计可以减少网络的参数量并提升运算速度,使高度非均匀模糊图像也能更加接近真实的复原。
2.4 损失函数损失函数部分由对抗损失函数Ladv和多尺度内容损失函数Lcont组成。总体损失函数Ltotal可以表示为
| $ {L_{{\rm{total}}}} = {\rm{ }}\lambda {\rm{ }}\cdot{L_{{\rm{adv}}}} + {L_{{\rm{cont}}}}, $ | (8) |
其中:λ为权重系数,通过实验对比分析,这里取λ=10-4。
1) 对抗损失函数
对抗损失函数其实就是生成对抗网络自身的损失函数,使用WGAN(Wasserstein GAN)模型[11]的Wasserstein-1距离W(q, p)去估计Jensen-Shannon散度,对每个独立的样本施加梯度惩罚,达到了目前稳定性最强的训练效果,其函数表达式为
| $ {L_{{\rm{adv}}}} = \sum\limits_{n = 1}^N {} [ - D(G({I^B}))], $ | (9) |
其中:IB为生成图片。
2) 多尺度内容损失函数
为了尽可能生成和原始清晰图像相似的像素空间输出,在每一个尺度上分别使用L2损失函数,多尺度内容损失函数可以表示为
| $ {L_{{\rm{cont}}}} = \sum\limits_{i = 1}^n {} {N_i}\left\| {{\rm{ }}{I_i} - {S_i}} \right\|_2^2, $ | (10) |
其中:Ii和Si分别是第i(i=1,2,3)层网络的复原图像和对应清晰图像;Ni表示在第i尺度图像上所有通道的像素个数。
3 实验结果与分析 3.1 实验设置本实验在Linux操作系统下基于TensorFlow深度学习框架实现,计算机硬件环境为3.9 GHz的i7处理器台式机,GPU参数为RTX2080Ti, 32 GB RAM。由于样本数据量比较小,初始学习率设为1×10-4,然后使用指数衰减法逐步减小学习率,衰减系数为0.3。使用Adam优化器[12]对损失函数进行优化,令β1=0.9,β2=0.999,ε=1×10-4,将batchsize设置为1,当训练2 000轮时学习率会衰减至1×10-6,此时网络达到收敛状态。
3.2 评价指标图像质量的好坏需要使用相应的评价指标进行描述,本文综合使用峰值信噪比(PSNR)、结构相似性(SSIM)和平均意见得分(MOS)对图像进行多方位评估。
1) 峰值信噪比(PSNR)。PSNR是基于复原图像x和真实图像y对应像素点间的误差,数学表达式为
| $ PSNR = {\rm{ }}20 \times {\rm{lg}}\frac{{{x_{\max}}}}{{\sqrt {\frac{1}{{m \times n}}{\rm{ }}\sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {} } {\rm{ }}{{\left\| {x\left( {i, j} \right) - y\left( {i, j} \right)} \right\|}^2}} }}, $ | (11) |
其中:m为图像的高度;n为图像的宽度;xmax表示图像点颜色的最大值。PSNR数值越大,表示图像质量越高。
2) 结构相似性(SSIM)。SSIM分别从亮度、对比度和结构三方面来度量图像的相似性,数学表达式为
| $ SSIM = {\rm{ }}\frac{{[2{u_x}{u_y} + {{({c_1}L)}^2}][2{\sigma _{xy}} + {{({c_2}L)}^2}]}}{{[{u_x^2} + {u_y^2} + {{({c_1}L)}^2}][{\sigma _x^2} + {\sigma _y^2} + {{({c_2}L)}^2}]}}, $ | (12) |
其中:ux和uy表示图像x和y的均值;σx、σy和σxy分别表示图像x和y的方差和协方差;c1、c2是用于维持稳定的常量;L表示像素值的动态变化范围。SSIM取值范围为[0, 1],其值越大,表示生成图像复原效果越好。
3) 平均意见得分(MOS)。本实验还使用观察者的视觉直观感知作为图像质量辅助衡量标准。由n个评分员对同一数据集不同场景下得到的复原图像按照5分制来打分,分值1~5分别代表图像质量非常差、差、一般、好和非常好。
不同复原结果得分先求和再取平均,即为最终的MOS,数学表达式为
| $ MOS = \frac{{\sum\limits_{i = 1}^n {} {y_i}}}{n}, $ | (13) |
其中:yi表示每个评分员对图像质量的直观视觉打分。
3.3 实验对比及分析 3.3.1 GoPro数据集GoPro数据集在图像去模糊领域较为常用且非常经典,该数据集包含车辆、行人和街景等分辨率为720×1 280的3 214对模糊和清晰图像,分为训练和测试两个部分。训练时,将数据集剪裁为256×256像素的图像块,采用由粗到精的训练思路;测试时,保持原始图片尺寸大小不变,直接进行清晰化复原。
使用GoPro数据集中道路交通场景,将本文方法与DeblurGAN方法[4]、DMPHN方法[5]、RAND方法[6]的复原结果进行对比,结果如图 8所示。可以看出,对于本文方法而言,场景1和场景2放大区域去模糊后,车牌中数字内容明显得到了较好复原,图像局部细节和整体轮廓的清晰度也得到了很大提升,然而其他三种方法得到的图像仍较为平滑。场景3放大区域去模糊后,本文方法的图像伪影明显减少,在去除模糊的同时边缘细节得到了较清晰的复原。

|
图 8 不同方法的去模糊效果对比 Fig. 8 Comparison of deblurring effects of different methods |
不同方法的图像质量评价结果见表 2。可以看出,相比DeblurGAN方法、DMPHN方法和RAND方法,本文方法的评价指标有较大提升。高质量且稳定的复原结果为道路交通的智能化发展提供了理论依据。
|
|
表 2 不同方法的图像质量评价结果 Tab. 2 Image quality evaluation results of different methods |
为了验证多尺度编解码网络在真实场景下的去模糊性能,搜索了不同道路交通场景下的真实模糊图像,并使用预训练好的YOLOv3模型[13]进行目标检测。使用去模糊前后图像中物体被检测的概率来检验去模糊效果,目标检测对比如图 9所示。可以看出,经本文方法处理后,道路交通图像的清晰度得到了明显提升,图中上边场景中被检测到的车辆明显增多,下边场景中黑色汽车被检测到的概率从0.589提升到0.855。并且,复原后的图像中车内司机也以0.598的概率得以检测,间接证明了在不同真实道路交通场景下本文去模糊方法的有效性。

|
图 9 去模糊前后目标检测对比 Fig. 9 Comparison of target detection before and after deblurring |
本文以道路交通模糊图像为研究对象,系统分析了当今深度学习去模糊方法的不足,设计了优化多尺度残差块结构,并基于多尺度图像复原策略提出了一种多尺度编解码生成对抗网络。仿真结果表明,经本文方法处理后的图像在多项评价指标上优于近些年的一些经典方法,在GoPro数据集和真实道路交通场景下可以得到整体和细节均有较高质量的复原结果。
| [1] |
陈书贞, 曹世鹏, 崔美玥, 等. 基于深度多级小波变换的图像盲去模糊算法[J]. 电子与信息学报, 2021, 43(1): 154-161. CHEN S Z, CAO S P, CUI M Y, et al. Image blind deblurring algorithm based on deep multi-level wavelet transform[J]. Journal of electronics & information technology, 2021, 43(1): 154-161. (  0) 0) |
| [2] |
黄正源, 谢维成, 黄化入, 等. 图像运动模糊还原技术综述[J]. 计算机工程与应用, 2020, 56(24): 28-34. HUANG Z Y, XIE W C, HUANG H R, et al. Overview of motion deblurring techniques for images[J]. Computer engineering and applications, 2020, 56(24): 28-34. (  0) 0) |
| [3] |
王一斌, 郑佳, 吕卓纹, 等. 波长相关物理成像模型的交通监控图像去雾算法[J]. 光子学报, 2019, 48(9): 227-236. WANG Y B, ZHENG J, LYU Z W, et al. Traffic monitoring image dehazing algorithm based on wavelength related physical imaging model[J]. Acta photonica sinica, 2019, 48(9): 227-236. (  0) 0) |
| [4] |
KUPYN O, BUDZAN V, MYKHAILYCH M, et al. DeblurGAN: blind motion deblurring using conditional adversarial networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2018: 8183-8192.
(  0) 0) |
| [5] |
ZHANG H G, DAI Y C, LI H D, et al. Deep stacked hierarchical multi-patch network for image deblurring[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2019: 5971-5979.
(  0) 0) |
| [6] |
PUROHIT K, RAJAGOPALAN A N. Region-adaptive dense network for efficient motion deblurring[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2020: 11882-11889.
(  0) 0) |
| [7] |
GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]//Proceedings of the Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2014: 2672-2680.
(  0) 0) |
| [8] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2016: 770-778.
(  0) 0) |
| [9] |
LI J C, FANG F M, MEI K F, et al. Multi-scale residual network for image super-resolution[C]//Proceedings of the European Conference on Computer Vision. Cham: Springer International Publishing, 2018: 527-542.
(  0) 0) |
| [10] |
JOHNSON J, ALAHI A, LI F F. Perceptual losses for real-time style transfer and super-resolution[C]//Proceedings of the European Conference on Computer Vision. Cham: Springer International Publishing, 2016: 694-711.
(  0) 0) |
| [11] |
ARJOVSKY M, CHINTALA S, BOTTOU L. Wasserstein GAN[EB/OL]. [2021-02-15]. https://www.researchgate.net/publication/313044478.
(  0) 0) |
| [12] |
KINGMA D, BA J. Adam: a method for stochastic optimization[EB/OL]. [2021-02-15]. https://www.researchgate.net/publication/269935079.
(  0) 0) |
| [13] |
REDMON J, FARHADI A. YOLOv3: an incremental improvement[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2018: 89-95.
(  0) 0) |
 2022, Vol. 54
2022, Vol. 54


