2. 西南交通大学 计算机与人工智能学院 四川 成都 611756;;
3. 莆田学院附属医院 福建 莆田 351100
2. School of Computing and Artificial Intelligence, Southwest Jiaotong Univeristy, Chengdu 611756, China;
3. Putian College Affiliated Hospital, Putian 351100, China
股票是社会生产力发展的产物,顺势而生的股票市场为企业主体进行融资提供了平台,并促进了资金的供求平衡。通过股票市场,个人投资者以及金融机构可以进行金融投资以期获得预期收益,市场上的变动密切关系到相关投资者的切身利益。同时,随着经济市场化的进程不断推进,股票已然成为我国国民经济的重要组成部分,与国家的宏观经济息息相关,它的运行情况反映了个体企业的运营境况、国民经济的发展态势和宏观经济的健康状况。因此,股票市场分析一直以来都备受学术界和业界的广泛关注。
为了避免对多只股票分别建模的冗余操作,许多金融机构或证券交易所编制了由多只代表性股票汇总得到的股票指数。对股票指数的建模不仅可以同时对多只股票进行分析,而且可以观察某个股票市场的整体情况。尽管如此,原始的股指数据往往是只包含历史信息的单一时间序列,这使得建模可用的信息有限。同时,原始股指序列具有非线性和非平稳性的特点,而且往往还包含大量的噪声和无用信息。这使得传统时序预测的方法无法得到较高的预测精度。针对这一问题,本文提出了一种基于时频融合卷积神经网络的预测方法。首先通过使用变分模态分解(variational mode decomposition, VMD)将原始序列分解为多个不同时间尺度的本征模态子序列(intrinsic mode function, IMF),其中的低频序列较原序列有着更明显的趋势。这保证了提取的历史信息更有效,也降低了原序列的噪声和非平稳性。然后,利用时序卷积网络(temporal convolutional network, TCN)分别对这些时频特征子序列进行建模并预测。进一步,通过VMD的逆分解操作,将子序列融合为股指序列的预测结果。最后在多个实际数据集上进行了实验,实验结果表明我们的模型比其他一些基准模型具有更高的预测精度。
本文的主要贡献包括:
1) 首次将变分模态分解(VMD)方法引入到股指预测模型中,利用VMD将噪声多、不平稳、非线性的原始股指序列数据分解成多个更具有规律性的模态子序列,降低了直接使用预测模型提取原序列有效信息的难度,提高了预测的精度;
2) 提出了一种基于时频融合卷积神经网络的股指预测方法。将原始股指数据通过VMD分解后得到的多条时频信号数据分别输入到TCN中,然后对输出的结果进行有效融合,得到股指序列的预测值。在几个真实数据集上的实验结果表明我们的方法具有更高的预测精度,同时具有更好的解释性。
1 相关工作时间序列分析具有相对完整的理论体系,发展至今产生了许多经典的预测模型。差分整合移动平均自回归模型(autoregressive integrated moving average model, ARIMA)被应用于股价的预测,短期预测取得了较好的结果[1-2]。由于金融时间序列具有异方差等特点,自回归条件异方差模型(autoregressive conditional heteroskedasticity, ARCH)及其广义变体(generalized autoregressive conditional heteroskedasticity, GARCH)也被广泛运用在金融时序分析中。魏宇将GARCH运用在沪深300指数上,对其波动率进行了预测[3];Hassan则使用隐马尔科夫(hidden markov model, HMM)模型对股票市场建模,并得到了较为准确的预测结果[4];朱永明结合粗糙集理论,使用不同指标对股市进行建模分析[5]。上述单一的传统统计学模型具有形式简单、可解释性强等特点,但其模型系数的规模通常不大,函数的形式也相对简单,所以其拟合能力较为有限。
除了传统统计学模型,机器学习中的一些模型也常用于时间序列预测。支持向量回归(support vector regression, SVR)是机器学习模型中经典的回归模型。Meesad等使用SVR结合了不同窗口设置方法对股票数据进行建模,验证了这一模型的有效性[6]。随着建模的数据量越来越大,涉及的数据类型也更加灵活多变。深层神经网络(deep neural network, DNN)在处理大数据问题上具有独特优势,其在金融时间序列预测上的有效性也被证明[7];姚宏亮等结合贝叶斯神经网络和均线滞后特征,提出了DSMA模型,并对模型效果进行了实验证明[8]。DNN的发展衍生出不同结构的模型,如循环神经网络(recurrent neural network, RNN)及其变体、卷积神经网络(convolutional neural networks, CNN)[9]及其变体。杨青等使用长短期记忆(long short-term memory, LSTM)对全球共30个股票指数进行不同期限研究,验证了LSTM的良好表现[10];文献[11]使用粒子群优化算法(particle swarm optimization, PSO)优化的分位数回归神经网络(quantile regression neural network, QRNN)对8个金融数据进行建模,都取得了较好的结果。上述模型在解决数据非线性、不连续和高维的问题上具有一定的优势,但是它们都是直接对原始单时间序列进行建模,模型精度往往受到噪声、非平稳以及有限信息等因素的影响。
真实世界的原始序列往往包含多重信息,其中还掺杂部分噪声与冗余无用的内容。为了解决这种问题,熊志斌结合神经网络,使用ARIMA对美元等三种汇率进行建模,并使用PSO对神经网络进行优化[12];Du通过对ARIMA和BPNN的复合模型证实了股票数据的非线性,同时预测的结果更加精确[13]。针对金融时间序列的非平稳、噪声多等特点,Hsieh等结合Haar小波分解与人工蜂群算法优化的RNN对DJIA等四只股票指数进行建模,验证了模型的预测精度[14];Cao等使用自适应白噪声完整经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)与LSTM对SPX等四只股票指数进行建模,并以SVR等模型作为基准方法进行对比实验,验证了所提出模型的优越性[15]。上述模型具有一定的效果,然而在实际应用中容易产生模态混叠,同时预测效果不够高。
综上所述,尽管以上的方法已经取得了一些较好的结果,然而在处理噪声多、非线性以及非平稳的股指序列数据时仍然存在一定的局限性。本文通过提取股指序列数据的时频特征,同时结合TCN和VMD给出了基于时频融合卷积网络的股指序列预测模型,并通过对比实验及可视化分析进行验证。
2 基础理论介绍本节主要介绍与所提出模型有关的基础理论知识。
2.1 变分模态分解(VMD)VMD是2014年提出的一种完全非递归的变分模式分解方法[16],它与经验模态分解(empirical mode decomposition, EMD)[17]、CEEMDAN[18]等同属于自适应信号分解方法,旨在根据数据自身时间尺度特征进行信号分解。同时,VMD避免了模态混叠等问题,并具有更坚实的数学基础。
在VMD算法中,每个模态都是由调幅-调频信号来表示的,定义为
| $ u_k( t) = A_k( t) {\rm{cos}}( {\mathit{Φ}}_k( t) ) , $ | (1) |
式中:Ak(t)是uk(t)的幅值;Φk(t)是相位;uk(t)的瞬时频率为ωk(t)≥0。在足够长的区间[t-δ, t+δ],δ≈2π/ωk(t)上,可以将模态视为谐波信号。先通过希尔伯特变换,获得uk(t)的解析信号的单边频谱;进一步,对于每种模式,与各自估计的中心频率的指数混合,将每个模式的频谱移至“基带”;最后,通过解析信号的高斯平滑度,即其导数的二范数的平方,来估计各模态的带宽。上述步骤产生的约束变分问题为
| $ \begin{array}{l} \min\limits_{\left\{u_{k}\right\}, \left\{\omega_{k}\right\}}\left\{\sum\limits_{k=1}^{K}\left\|\partial_{t}\left[\left(\delta(t)+\frac{\mathrm{j}}{{\mathtt{π}} t}\right) * u_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|_{2}^{2}\right\}\\ \text { s. t. } \sum\limits_{k=1}^{K} u_{k}(t)=f(t) \text {, } \end{array} $ | (2) |
其中:f是原始信号;uk(k=1, 2,…,K)是所有的模态的集合; ωk(k=1, 2,…,K)是对应中心频率的集; j是虚数单位。对上式进行递归求解,就可以得到想要的模态分量。
2.2 时序卷积网络(TCN)CNN是被广泛运用的一种神经网络,其核心是通过卷积计算来提取局部的数据特征。为了使得模型更加适合序列学习,并避免梯度问题,TCN在CNN的基础上加入了如下特殊结构[19]。
1) 因果卷积:因果卷积在WaveNet中第一次被提出[20],它将层之间的信息传递方向限制成单一方向,这符合时序任务只能获取历史信息的要求。
2) 膨胀卷积:CNN难以处理序列学习问题,这主要是因为它不具备抓取长时依赖信息的能力。受限于卷积核大小,CNN需要不断叠加卷积层来获得更长期的感受野,这会导致参数体量庞大等问题。膨胀卷积则采用了间隔采样的方法,在层数较少的情况下网络可以获得更大的感受野。
3) 残差连接:神经网络的表达能力一定程度上随着网络层数的增加而提升,但训练难度也随之增加,容易出现梯度消失等问题。残差连接的输出被表述成输入与输入的非线性函数的线性求和,这实现了信息的跨层传递。同时,若网络通过链式法则进行反向传播,整个输出项的梯度经过多次连乘后不会接近消失。
3 本文的方法上一节我们介绍了VMD和TCN的背景知识,以此为基础,详细介绍基于时频融合卷积神经网络的股指预测模型:首先,介绍模型的整体框架;然后,给出模型学习的具体过程。
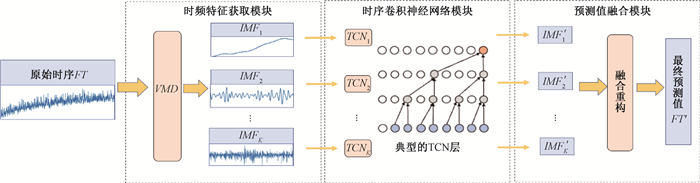
3.1 模型框架原始的股指序列数据包含噪声,而且是非平稳和非线性的。为此,本文用VMD将原始股指序列数据进行有效分解,得到多条具有时频信息的子序列。进而通过结合TCN,构建了基于时频融合的卷积神经网络模型。图 1是我们所提出模型的框架图,每个模块描述如下。
|
图 1 所提出模型的框架 Fig. 1 General framework of the proposed model |
1) 时频特征获取模块。设置VMD分解所需的模态数K,对原始股指序列数据FT进行VMD分解。获得原股指序列数据的K个基本模态分量,记为IMF1,…,IMFK,分别代表原序列从高频到低频的震荡成分。根据VMD的重构原理,用t代表时间序列中的时间戳,可得到
| $ \sum\limits_{k=1}^{K} I M F_{k}(t)=F T(t) 。$ | (3) |
使用max-min归一化,
| $ I M F_{-} S_{k}(t)=\frac{I M F_{k}(t)-\min \left(I M F_{k}(t)\right)}{\max \left(I M F_{k}(t)\right)-\min \left(I M F_{k}(t)\right)},$ |
其中:min(IMFk(t))、max(IMFk(t))代表的是计算序列中的最小值和最大值,标准化操作后得到IMF_Sk。为了进行向前一步预测,本文构造了滑动窗口,并确定时间窗口的长度t=L。按照时间窗口构建输入特征和输出特征,得到Xk、Yk,再按照训练测试比将其划分为Xk_train、Yk_train和Xk_test、Yk_test。
2) 时序卷积神经网络模块。使用Xk_train、Yk_train对模型进行训练,为了避免过长训练时间,并减少过拟合的风险,引入早停机制。针对输入了不同时频特征数据的TCN网络,本文设定了不同的参数使其更具有针对性。通过训练集的参数优化得到网络参数,再使用训练好的模型对Xk_test进行预测,得到预测结果为Y′ k_test,对其进行反标准化,得到IMF′ k_test。
3) 预测值融合模块根据公式(3),将每个TCN网络得到的子序列预测进行重构,最终得到的时间序列预测结果为FT′test。
3.2 模型学习过程这一部分将着重对模型的学习过程进行介绍。分解过程中,单一的股指序列数据被对应分解成K个模态子序列,优化的目标函数如式(2)所示。记原始股指序列数据为FT ∈ RT,其对应子序列为IMF1,…,IMFK。利用二次惩罚项与拉格朗日乘数法将式(2)变成如下的无约束优化问题,
| $ \begin{array}{l} L\left(\left\{I M F_{k}\right\}, \left\{\omega_{k}\right\}, \lambda\right):=\alpha \sum\limits_{k=1}^{K} \| \partial_{t}\left[\left(\delta(t)+\frac{\mathrm{j}}{{\mathtt{π}} t}\right) *\right. \\ \left.I M F_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t}\left\|_{2}^{2}+\right\| F T(t)-\sum\limits_{k=1}^{K} I M F_{k}(t) \|_{2}^{2}+ \\ \left\langle\lambda(t), F T(t)-\sum\limits_{k=1}^{K} I M F_{k}(t)\right\rangle ,\end{array} $ |
其中:α为二次惩罚因子,作用是在有噪声时保证重构的精度;λ(t)是拉格朗日乘子。
用交替方向乘子法(alternating direction method of multipliers, ADMM)对IMFkn+1、ωkn+1和λn+1进行更新,优化过程如算法1中的1)~6)。
预测过程中,TCN的输入为IMF_Sk。膨胀卷积使得网络的感受野更大,针对一维的输入向量C ∈ Rn和过滤器f: {0, …, k-1}→ R,膨胀卷积可以表示为
| $ F(t)=\left(\boldsymbol{C} \cdot f_{d}\right)(t)=\sum\limits_{i=0}^{k-1} f(i) \cdot X_{t-d i} ,$ |
其中:d是膨胀系数;k是滤波器大小;t-di表明了历史信息的方向。同时,TCN模型中还使用残差连接:z(i)为残差块输出;z(i-1)为残差块的输入;m()为非线性映射,则残差连接为
| $ z^{(i)}=m\left(z^{(i-1)}\right)+z^{(i-1)} 。$ |
将上述的膨胀卷积和残差连接合并记为tcn(),其中给定超参数μk,需要学习的参数记做θk。对所提出的基于时频融合卷积神经网络使用BP反向传播进行参数优化,优化方法为梯度下降法。假设时间窗口长度为L,预测期长τ,那么输入、输出对数量为N=T-L-τ+1,且Xk∈ RN·T,Yk∈ RN·τ。我们将很容易得到,Y′k=tcn(Xk; θk)。训练过程中,使用均方误差MSE作为损失函数,记Xk_train的第n行为xkn,Yk_train的第n行为ykn,得到训练的目标函数为
| $ M S E_{k}=\frac{1}{N} \sum\limits_{n=1}^{N}\left(y_{k n}-t c n\left(x_{k n} ; \theta_{k}\right)\right)^{2} 。$ |
原始序列共分解成K个子序列,需要同时进行K个上述优化,算法1给出了这一过程。
算法1 基于时频融合卷积神经网络模型的优化算法
输入:原始时间序列FT;相关参数K、L、T、τ、κ;神经网络超参数μk;早停参数patience。
输出:训练期的预测值FT′test。
初始化:{IMFk1},{ωk1},λ′1, n←0;TCN中所有的可学习参数θk。
1) repeat n←n+1 //数据预处理
2) for k=1∶K,执行
3) 针对ω≥0,更新IMFk和ωk
| $ \begin{array}{l} I M F_{k}^{n+1}(\omega) \leftarrow \frac{1}{1+2 \alpha\left(\omega-\omega_{k}^{n}\right)^{2}} \cdot \\ \left\{F T(\omega)-\sum\limits_{i<k} I M F_{i}^{n+1}(\omega)-\sum\limits_{i>k} I M F_{i}^{n}(\omega)+\right. \\ \left.\frac{\lambda^{\prime n}(\omega)}{2}\right\} \omega_{k}^{n+1} \leftarrow \frac{\int_{0}^{\infty} \omega\left|I M F_{k}^{n+1}(\omega)\right|^{2} \mathrm{~d} \omega}{\int_{0}^{\infty}\left|I M F_{k}^{n+1}(\omega)\right|^{2} \mathrm{~d} \omega} \end{array} $ |
4) End for
5) 针对ω≥0,采用对偶上升法
| $ \begin{array}{c} \lambda^{\prime n+1}(\omega) \leftarrow \lambda^{\prime n}(\omega)+\kappa(F T(\omega)- \\ \left.\sum\limits_{k} \operatorname{IMF}_{k}^{n+1}(\omega)\right) \end{array} $ |
6) until:
7) for k=1∶K,使用min-max标准化,得到IMF_Sk,构造得到Xk_train、Yk_train和Xk_test、Yk_test
8) for n=1∶N执行 //参数优化
9) repeat
针对(Xk_train, Yk_train)使用BP最小化MSEk,更新参数θk
10) until满足早停条件,记录θ′ k, tcnk
11) end for
Y′k_test=tcnk(Xk_test; θk),反标准化得到IMF′k_test,从而FT′test=
12) end for
4 时频融合卷积神经网络的股指预测实验分析 4.1 数据集和实验环境本文选取了国内外6只股票指数的每日收盘指数,数据均来自国泰君安数据库CSMAR的股票市场分析模块(https://cn.gtadata.com/)。选取的指数分别是标准普尔500指数(Standard and Poor 500 Index, SPX)、纳斯达克综合指数(IXIC)、日经指数225(Nikkei 225, N225)、阿姆斯特丹泛欧指数(Amsterdam Stock Exchange, AEX)、香港恒生指数(Hang Seng Index, HSI)和上证综合指数(Shanghai Securities Composite Index, SSE),其范围涵盖了多个国家和地区,兼具代表性和地区特点。选择的时间跨度为2010年1月4日—2019年12月4日,由于不同市场上节假日等因素的影响,不同股票数据在序列长度上略有差异。实验中使用80%的数据作为训练集,剩下20%作为测试集。实验所使用的设备搭载主频为2.1 GHz的CPU,程序编程环境是Anaconda3、Python3.7和Tensorflow-CPU。
4.2 对比实验与参数设置为了验证所提出模型的有效性,本文使用统计模型中的ARIMA[1]、GARCH[21]、HMM[22]机器学习中的SVR[23]和神经网络中的LSTM[10]、TCN[24]模型以及C-LSTM[15]、C-TCN[25]模型(C表示CEEMDAN)作为基准模型,它们都曾被应用于股票指数等时间序列的预测问题。引入常用的三种评价指标:均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)。设n是测试集的长度,三者的基本计算公式分别为
| $ \begin{aligned} M A E &=\frac{1}{n} \sum\limits_{i=1}^{n}\left|F T_{\text {test }}^{\prime}(i)-F T_{\text {test }}(i)\right|, \\ R M S E &=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(F T_{\text {test }}^{\prime}(i)-F T_{\text {test }}(i)\right)^{2}, } \\ M A P E &=\frac{100 \%}{n} \sum\limits_{i=1}^{n}\left|\frac{F T_{\text {test }}^{\prime}(i)-F T_{\text {test }}(i)}{F T_{\text {test }}(i)}\right| 。\end{aligned} $ |
我们对模型进行了30次重复实验来避免偶然性,并计算平均指标作为最终对比的准则。所有预测模型都采用了网格调参的方法,其中TCN的主要参数及调节范围如表 1所示。
|
|
表 1 TCN的参数表 Tab. 1 The parameters table of TCN |
表 2、3、4分别是9个模型对6个数据集重复30次建模后计算的RMSE、MAE和MAPE指标平均值,小括号内为标准差,黑体为最优值。SVR等模型由于重复实验结果不变,因此标准差为0。不同模型在三个指标上的表现基本一致,仅考虑指标RMSE,最优模型为本文提出的模型,其在数据集HSI上较C-TCN提升34%,在SPX上较C-LSTM提升31%。实证结果表明基于时频融合的方法有利于提升预测模型的性能:首先,将原始时序分解成相对平稳的时频特征子序列,可以进一步提取出趋势和噪声项;其次,使用TCN对子序列进行建模,发挥其高效的学习能力,实现了对序列的高精度预测。
|
|
表 2 对比实验的RMSE Tab. 2 RMSE of the comparative experiments |
|
|
表 3 对比实验的MAE Tab. 3 MAE of the comparative experiments |
|
|
表 4 对比实验的MAPE Tab. 4 MAPE of the comparative experiments |
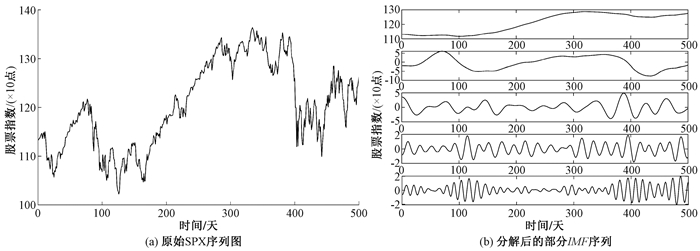
本小节以SPX收盘指数序列作为一个实例,对模型的不同阶段进行可视化。首先,对原始序列进行可视化,如图 2(a)所示。
|
图 2 VMD分解前后序列 Fig. 2 Sequences before and after VMD |
该序列呈现出整体上的长期趋势,这为使用模型进行预测提供了一定的依据。此外,序列具有波动性大、噪声多和非线性等特点,对它构建传统的线性预测模型将难以获得高精度的预测结果。神经网络模型更适合用来处理这类数据,这与上一节的实验结果相一致。
对原始序列进行VMD,得到的部分IMF序列如图 2(b)所示。图中从上至下,子序列的频率递增,其中频率最低的为IMF1,代表了股指序列的整体走向,其明显比原始SPX序列更加平滑。整体来看,图 2(b)中的低频序列具有明显的变化趋势,它们具有波动相对小、噪声相对少的特点。
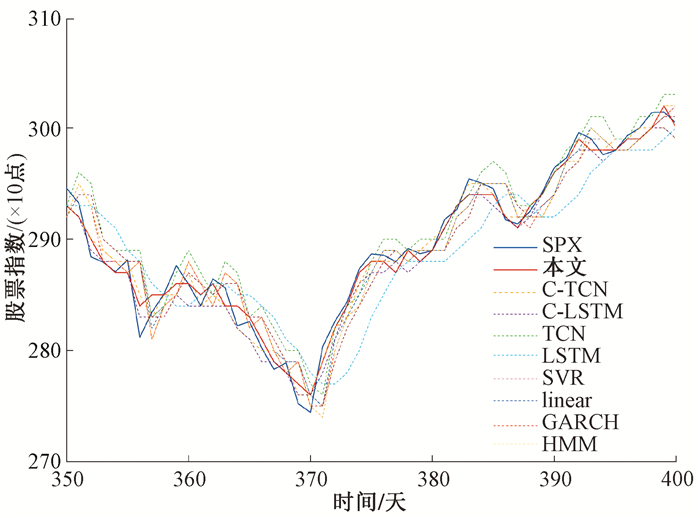
针对得到的每个IMF序列,设置时间窗口长度为4,构造TCN对未来一期的数据进行预测。得到每个IMF序列的预测结果后,将预测结果融合得到SPX股指预测值,如图 3所示。
|
图 3 模型预测结果 Fig. 3 The forecast result of the model |
其中:橙线是本文方法预测值;蓝线为真实序列;虚线是其他基准模型。两条实曲线重合度较高,这表明本文提出的模型的预测结果与真实数据基本一致,模型可以获得很好的预测结果。
5 总结与展望本文提出了基于时频融合卷积神经网络的股票指数预测模型。实验中选取实际股票市场中具有代表性的6只股票指数,以常用于股票指数预测的8个模型作为对比基准,计算了每个模型预测结果的3个评价指标,实验证明本文提出的模型相对于其他基准模型获得了更好的预测效果,RMSE较其他模型提升最高达到34%。不仅如此,此模型也可以扩展到其他的应用领域。我们研究的仅仅是基于单时间序列历史信息的预测问题,但在实际的研究中,许多宏、微观指标,如汇率、利率等,以及其他一些股指的技术指标都被证明对股票指数的变化有影响,后续工作将考虑引入这些信息来有效融合模型的输入特征。此外,文本挖掘和自然语言处理通过对金融新闻进行情感分析,可以掌握投资者和市场的需求动向,将它们考虑进模型也为未来的工作提供了思路。
| [1] |
ARIYO A A, ADEWUMI A O, AYO C K. Stock price prediction using the ARIMA model[C]//The 16th International Conference on Computer Modelling and Simulation. Piscataway: IEEE Press, 2014: 106-112.
(  0) 0) |
| [2] |
WICHAIDIT S, KITTITORNKUN S. Predicting SET50 stock prices using CARIMA (cross correlation ARIMA)[C]//International Computer Science and Engineering Conference. Piscataway: IEEE Press, 2015: 1-4.
(  0) 0) |
| [3] |
魏宇. 沪深300股指期货的波动率预测模型研究[J]. 管理科学学报, 2010, 13(2): 66-76. WEI Y. Volatility forecasting models for CSI300 index futures[J]. Journal of management sciences in China, 2010, 13(2): 66-76. (  0) 0) |
| [4] |
HASSAN M R, NATH B. Stock market forecasting using hidden Markov model: a new approach[C]//The 5th International Conference on Intelligent Systems Design and Applications. Piscataway: IEEE Press, 2005: 192-196.
(  0) 0) |
| [5] |
朱永明. 基于粗糙集理论的股市预测研究[J]. 郑州大学学报(理学版), 2009, 41(4): 40-44. ZHU Y M. Study on prediction of stocking market based on rough set theory[J]. Journal of Zhengzhou university (natural science edition), 2009, 41(4): 40-44. (  0) 0) |
| [6] |
MEESAD P, RASEL R I. Predicting stock market price using support vector regression[C]//2013 International Conference on Informatics, Electronics and Vision. Piscataway: IEEE Press, 2013: 1-6.
(  0) 0) |
| [7] |
HEATON J B, POLSON N G, WITTE J H. Deep learning in finance[EB/OL]. (2018-01-04)[2021-05-03]. https://arxiv.org/pdf/1602.06561.pdf.
(  0) 0) |
| [8] |
姚宏亮, 艾刘可, 王浩, 等. 均线滞后的时序自回归股市态势预测算法[J]. 郑州大学学报(理学版), 2018, 50(3): 60-66. YAO H L, AI L K, WANG H, et al. Time series autoregressive stock market forecasting algorithm based on moving average hysteresis[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(3): 60-66. (  0) 0) |
| [9] |
李艳灵, 杨志鹏, 王莎莎, 等. 基于卷积神经网络进行电影院人群分布统计[J]. 信阳师范学院学报(自然科学版), 2020, 33(4): 675-680. LI Y L, YANG Z P, WANG S S, et al. The distribution of cinema population based on convolutional neural network[J]. Journal of Xinyang normal university (natural science edition), 2020, 33(4): 675-680. DOI:10.3969/j.issn.1003-0972.2020.04.028 (  0) 0) |
| [10] |
杨青, 王晨蔚. 基于深度学习LSTM神经网络的全球股票指数预测研究[J]. 统计研究, 2019, 36(3): 65-77. YANG Q, WANG C W. A study on forecast of global stock indices based on deep LSTM neural network[J]. Statistical research, 2019, 36(3): 65-77. (  0) 0) |
| [11] |
PRADEEPKUMAR D, RAVI V. Forecasting financial time series volatility using particle swarm optimization trained quantile regression neural network[J]. Applied soft computing, 2017, 58: 35-52. DOI:10.1016/j.asoc.2017.04.014 (  0) 0) |
| [12] |
熊志斌. ARIMA融合神经网络的人民币汇率预测模型研究[J]. 数量经济技术经济研究, 2011, 28(6): 64-76. XIONG Z B. Research on RMB exchange rate forecasting model based on combining ARIMA with neural networks[J]. The journal of quantitative & technical economics, 2011, 28(6): 64-76. (  0) 0) |
| [13] |
DU Y L. Application and analysis of forecasting stock price index based on combination of ARIMA model and BP neural network[C]//Chinese Control and Decision Conference. Piscataway: IEEE Press, 2018: 2854-2857.
(  0) 0) |
| [14] |
HSIEH T J, HSIAO H F, YEH W C. Forecasting stock markets using wavelet transforms and recurrent neural networks: an integrated system based on artificial bee colony algorithm[J]. Applied soft computing, 2011, 11(2): 2510-2525. (  0) 0) |
| [15] |
CAO J, LI Z, LI J. Financial time series forecasting model based on CEEMDAN and LSTM[J]. Physica A: statistical mechanics and its applications, 2019, 519: 127-139. (  0) 0) |
| [16] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE transactions on signal processing, 2014, 62(3): 531-544. (  0) 0) |
| [17] |
RILLING G, FLANDRIN P, GONCALVES P. On empirical mode decomposition and its algorithms[C]//The 6th IEEE-EURASIP Workshop on Nonlinear Signal and Image ProcessingP Workshop on Nonlinear Signal and Image Processing. Piscataway: IEEE Press, 2003: 8-11.
(  0) 0) |
| [18] |
TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE Press, 2011: 4144-4147.
(  0) 0) |
| [19] |
CHUNG J, GULCEHRE C, CHO K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL]. (2014-12-11)[2021-04-15]. https://arxiv.org/pdf/1412.3555.pdf.
(  0) 0) |
| [20] |
OORD A V D, DIELEMAN S, ZEN H, et al. WaveNet: a generative model for raw audio[EB/OL]. (2016-09-19)[2021-03-28]. https://arxiv.org/pdf/1609.03499.pdf.
(  0) 0) |
| [21] |
LIN Z. Modelling and forecasting the stock market volatility of SSE composite index using GARCH models[J]. Future generation computer systems, 2018, 79: 960-972. (  0) 0) |
| [22] |
ZHANG X, LI Y X, WANG S Z, et al. Enhancing stock market prediction with extended coupled hidden Markov model over multi-sourced data[J]. Knowledge and information systems, 2019, 61(2): 1071-1090. (  0) 0) |
| [23] |
LAHMIRI S. Minute-ahead stock price forecasting based on singular spectrum analysis and support vector regression[J]. Applied mathematics and computation, 2018, 320: 444-451. (  0) 0) |
| [24] |
WANG X, WANG Y J, WENG B, et al. Stock2Vec: a hybrid deep learning framework for stock market prediction with representation learning and temporal convolutional network[EB/OL]. (2020-09-29)[2021-05-03]. https://arxiv.org/pdf/2010.01197.pdf.
(  0) 0) |
| [25] |
WANG J, LUO Y Y, TANG L Y, et al. A new weighted CEEMDAN-based prediction model: an experimental investigation of decomposition and non-decomposition approaches[J]. Knowledge-based systems, 2018, 160: 188-199. (  0) 0) |
 2022, Vol. 54
2022, Vol. 54


