深度学习模型在图像识别和检测任务中取得了优异的成果[1-3]。然而,这些有监督的神经网络模型需要大量有标签的样本来训练参数,严重限制了这些模型对一些只有少量有标签样本的数据集的适用性。在满文识别研究中,传统的深度学习方法受制于满文数据集中有标签样本较少的问题,因此无法充分发挥强大的识别能力。目前有很多专家学者开始关注小样本学习问题。小样本学习问题是指在对测试实例进行测试之前,只能观察每个可能类的几个示例,以此为限制条件对测试样本进行分类,这种小样本学习问题称为K-shot学习。K-shot学习方法适用于小样本学习场景,因此在医疗诊断[4]、文本分类[5]、目标检测[6]、目标跟踪[7]等领域得到了广泛的应用。满文数据集类别很多,但每个类别中有标签的样本较少,因此满文识别可以视为一个典型的K-shot学习问题。但目前的K-shot学习研究大多只关注较小类别数量的分类问题,大类别场景下的K-shot学习算法没有得到广泛地关注,而在满文识别研究中算法需要面对极大的类别数,因此如何在大类别场景下利用K-shot学习方法获得较好的识别结果成为了一个挑战。
本文利用N元ECOC技术构建了一种大类别K-shot满文识别方法。本文的主要贡献包括3个方面:
1) 提出了一种在大类别场景下适用的K-shot学习算法,有效地提高了K-shot学习算法在大类别场景下的识别精度;
2) 提出基于N元ECOC的K-shot学习算法,利用N元ECOC编码矩阵将原本的大类别分类问题分解为一系列较小类别的分类问题进行处理,有效地减小了支持集信息的复杂度;
3) 在满文识别问题上的实验结果表明,提出的K-shot学习算法可以在满文的大类别分类场景下达到较高的识别准确率。
1 相关工作K-shot学习用于解决有标签样本数量不足的问题,通常可分为4类:基于微调的方法;基于数据增强的方法;基于元学习的方法和基于度量学习的方法。
基于微调的方法。基于微调(finetune)的方法[8]一般是在大规模数据上预训练模型,在目标小样本数据集上对神经网络模型的全连接层或顶端几层进行参数微调,得到微调后的模型即可进行K-shot识别任务。文献[9]提出了一种微调方法,主要包含以下几个机制:1) 在小样本类别上再训练的过程使用更低的学习率; 2) 在微调阶段使用自适应的梯度优化器; 3) 当源数据集和目标数据集之间存在较大差异时, 可以通过调整整个网络来实现。基于微调的方法虽然可以取得较好的效果,但是当目标数据集和源数据集分布并不类似时,模型在目标数据集上容易产生过拟合。
基于数据增强的方法。基于数据增强(data augmentation)的方法是借助辅助数据或辅助信息, 对原有的小样本数据集进行数据扩充或特征增强,利用扩充后的数据进行K-shot学习,主要可以分为基于无标签数据的方法和基于数据合成的方法。基于无标签数据的方法是指利用无标签数据对小样本数据集进行扩充,常见的方法有半监督学习[10]和直推式学习[11]等。文献[12]提出使用MAML[13]模型来进行半监督学习,利用无标签数据调整嵌入函数的参数,用带标签数据调整分类器的参数。文献[14]提出了转导传播网络,基于直推式学习的思想来解决K-shot学习问题,取得了很好的效果。基于数据合成的方法是指为小样本类别合成新的带标签数据来扩充训练数据,文献[15]提出将元学习与数据生成相结合,通过数据生成模型生成虚拟数据来扩充样本的多样性,并结合元学习方法,用端到端的方式共同训练生成模型和分类算法。基于数据增强的方法目前应用虽然较为广泛,也取得了很好的研究成果,但是生成的数据很难捕捉到原始数据复杂的数据分布,会对模型性能产生一定影响。
基于元学习的方法。在基于元学习的方法中,算法在元数据中进行学习,在处理新的学习任务时可以利用从元数据中得到的经验快速地对新的数据进行处理。文献[13]提出的MAML算法是一种与模型无关的元学习算法,该算法可以与使用梯度下降法优化的任何模型兼容,并且适用于不同的学习问题,包括分类、回归和强化学习等。Mishra等[16]提出了一类简单而通用的元学习架构,使用了时间卷积和软注意力的新颖组合。文献[17]提出了Meta network,它的快速泛化能力源自其“快速权重”的机制,在训练过程中产生的梯度被用来生成快速权重。此外,研究人员认为普通的梯度下降方法难以在小样本场景下进行拟合,因此可以通过调整优化方法来完成小样本分类任务。文献[18]提出的K-shot学习模型包含一个元学习器和一个基础学习器,其中元学习器用于学习元任务之间的泛化信息并使用记忆机制保存这种信息,基础学习器用于快速适应新的任务并和元学习器交互产生预测输出。以上基于元学习的方法都取得了很好的识别效果,为K-shot识别问题带来了很好的解决思路。
基于度量学习的方法。该方法是对样本间距离分布进行建模,使得属于同类的样本靠近,异类的样本远离。基于度量学习的K-shot方法通过度量测试集中样本和支持集中样本的距离,借助K近邻(K-nearest neighbor, KNN)[19]的思想完成分类,能够取得很好的分类效果。文献[20]提出的原型网络(prototypical networks)学习一个度量空间,在该空间中每个类别都存在一个“原型”,用来表达该类别的特征,以这种形式把分类问题转化为度量空间中的最近邻问题。文献[21]提出了一种关系网络(relation networks),该网络不再使用单一且固定的距离度量方式,而是训练一个网络来学习距离的度量。文献[22]提出了匹配网络(matching networks),并提出了目前常用的小样本学习数据组织方式:数据都以“片段(episode)”的形式进行组织,N-way 1-shot的任务片段是指由N种类别的单个样本组成支持集,并且由来自这N种类别的其他样本作为测试样本的一次训练或测试任务。以上基于度量学习的方法被广泛地应用于各种小样本场景下的识别问题中,并且也都取得了很好的效果。
尽管上述研究在小类别场景下取得了较好的效果,但没有考虑实际应用中常见的分类类别较大的情况。随着分类类别的增大,K-shot学习中的支持集类别信息逐步复杂化,过于复杂的支持集会导致K-shot学习算法的识别能力大幅下降。因此本文主要研究适用于大类别分类场景的K-shot学习算法,提出一种基于N元ECOC[23]的K-shot学习算法,其基本思想是利用N元ECOC技术对原本的大类别分类问题进行N元分解,将其分解为一系列小类别的分类问题,然后利用K-shot学习算法对这些小类别问题进行分类,再将分类结果进行合并和纠错,最终获得大类别分类结果。本文提出的方法通过N元ECOC分解降低了支持集信息的复杂度,所以取得了较好的分类结果。
2 本文方法 2.1 基本思想为解决大类别场景下的满文识别问题,我们提出了一种适用于大类别场景的K-shot学习模型,该模型的核心思想是利用N元ECOC技术将原始大类别分类问题分解为一系列更为简单的小类别分类子问题,然后交由基于K-shot学习模型构建的基分类器进行处理。与直接采用K-shot学习算法对大类别问题进行分类相比,采用N元分解策略不仅降低了支持集复杂度和基分类器的压力,而且可以利用编码矩阵进行纠错输出,因此本文提出的K-shot学习模型在大类别场景下的满文识别研究中获得了更好的识别结果,提升了识别准确率。
如表 1所示,以具有5个类别的4元ECOC编码为例,介绍N元ECOC编码矩阵(coding matrix)的构造过程。编码矩阵的每一个行编码都代表一个具体的类别,与传统的ECOC编码矩阵只有2元或3元不同,编码矩阵M由{1, 2,…, N}构成,其中N>3;编码矩阵的每列代表一个分类器,同时代表要对原类别进行的N元划分。对应上述编码,基于N元ECOC的K-shot学习模型主要包括4个步骤。
|
|
表 1 N元ECOC编码矩阵M Tab. 1 N-ary ECOC coding matrix M |
1) 通过从范围为{1, 2,…, N}的整数之间进行均匀随机采样生成N元ECOC编码矩阵M,如表 1所示。
2) 根据编码矩阵M中的每一列,将原始的支持集划分为N组(此处N=4),并构建一个新的K-shot学习模型基分类器。
3) 给定一个测试示例xt,使用全部K-shot学习基分类器对测试样本进行测试并输出对应类别,最后组成预测编码。例如f(xt)=[2, 2, 2, 1, 1, 3]。
4) 最后根据编码矩阵M的行编码(类别编码)和预测编码之间距离的最小值确定样本xt的最终类别。即最终预测标签yt是样本xt的预测编码最接近的类别,如yt=arg minid(f(xt), Ci)=2。其中d表示距离度量。
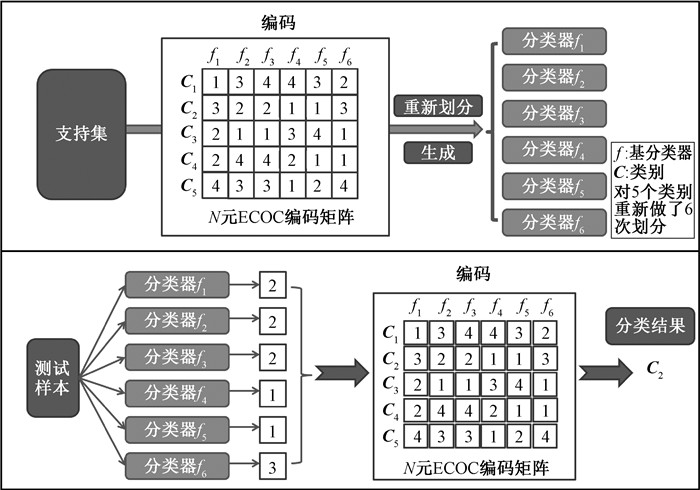
基于N元ECOC的K-shot学习模型的识别过程分为编码和解码两个阶段。在编码阶段,模型会将当前支持集依据编码矩阵M的列编码重新进行划分,并根据划分后的支持集生成多个K-shot学习基分类器,如图 1所示。图 1中,N元ECOC编码矩阵的列数为6,所以模型会将原支持集重新划分为6个子支持集,并根据子支持集信息生成f1~f6共6个K-shot学习基分类器。在解码阶段,输入一个测试样本,模型将测试样本分别输入到基分类器中进行分类。f1~f6基分类器分别输出测试样本对应的分类类别,并组成预测编码。最后,模型将计算当前测试样本的预测编码与编码矩阵M中的行编码(类别编码)之间的Hamming距离,并将与预测编码距离最近的一个类别编码作为测试样本的最终类别输出。
|
图 1 基于N元ECOC的K-shot学习模型框架 Fig. 1 Model framework of K-shot learning based on N-ary ECOC |
上述过程中,N元ECOC主要起到两个作用:1) N元ECOC编码将原本大类别的支持集划分成了较小的类别集合,而后再交给K-shot学习基分类器进行分类,这种分类方式减小了分类器的分类压力,能够获得更好的识别结果;2) 在模型的解码过程中将与预测编码距离最近的类别编码作为最终分类结果,可以实现对识别错误的纠错,从而进一步提升模型识别性能。综合以上两点,本文提出的K-shot学习模型在大类别识别问题上可以获得更好的识别效果。
2.2 编码过程传统的N元ECOC编码阶段,会生成一个编码矩阵来指导基分类器的训练和预测。编码矩阵由{1, 2,…, N}组成,矩阵的每一行代表一个类别,每一列代表一个基分类器。基分类器只负责训练对应列上非0编码对应类别的数据,并把所有训练数据重新按编码矩阵列上的编码进行划分,然后利用分成N类的训练数据训练基分类器,用同样的方法训练其他列对应的分类器。与使用传统分类器的N元ECOC不同,在本文算法的编码阶段,利用大小为L×Q的N元ECOC编码矩阵M=(Mij)L×Q,将原始支持集S变换为L个具有N个类别的支持集{Sl1≤l≤L},其中:Mij∈{1, 2,…, N};L为矩阵M的列数;Q为矩阵M的行数;1≤i≤Q,1≤j≤L。编码矩阵M的每一列对应一个具有N个分类的支持集。利用编码矩阵M的第l列元素Mil构造具有N个类别的支持集Sl,而后基于支持集Sl生成对应的K-shot学习基分类器fl。基分类器可以利用传统分类方法构建,如支持向量机等。传统N元ECOC编码对训练集进行划分,并用划分后的训练数据训练基分类器。而本文提出的模型中,编码阶段主要是对K-shot学习模型中的支持集进行编码,以此获得能够输出预测编码的K-shot学习基分类器。如图 1中利用行数(类别数)为5、列数(基分类器数量)为6的N(N=4)元ECOC编码矩阵M,将原始支持集S变换为6个具有4个类别的基分类器支持集。而后根据这6个子支持集生成对应的6个基分类器,完成模型的编码过程。
2.3 解码过程模型的解码过程在编码过程之后。利用编码得到一系列基分类器,模型的解码过程是用每个基分类器依次预测待测样本的类别并得到一个预测编码,将这个预测编码与编码矩阵M的每一个行向量进行比较,模型认为编码矩阵M中与预测编码相似度最高的行向量对应的类别就是待测样本的类别。本文使用Hamming距离进行相似度的计算,比较预测编码x与编码行Mi对应位置上数值不相等的个数即是Hamming距离。
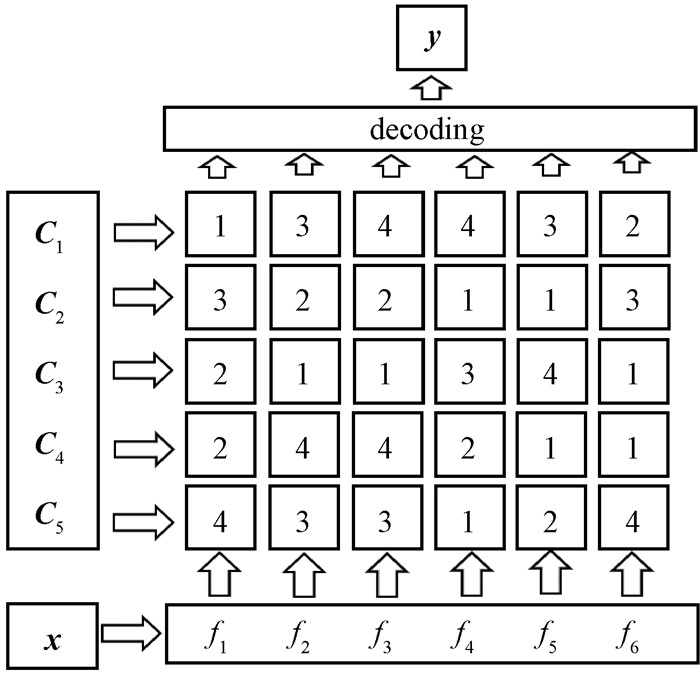
如图 2所示,假设一个待测样本x的预测编码是“[1, 3, 4, 4, 3, 2]”,它与向量C1, C2, C3, C4, C5对应行向量的Hamming距离分别是“0, 5, 5, 4, 4”。预测编码与C1对应行向量的距离最小,因此可以判定该待测样本属于C1类别。ECOC能够容忍一定数量的基分类器错误,编码的容错率与基分类器数量有关,正常情况下,基分类器的数量越多容错率越强。现假设存在某个类别为C1的样本点,所有的基分类器都预测正确的情况下,得到的预测编码为“[1, 3, 4, 4, 3, 2]”。但如果第3个分类器f3预测成错误结果“3”,预测编码变成“[1, 3, 3, 4, 3, 2]”。解码该预测编码得到与5个类别之间的Hamming距离为“1, 5, 5, 4, 3”,解码距离最小的类别仍然是正确类别C1。根据以上示例可以看出N元ECOC编码矩阵能够容忍小部分基分类器发生错误。
|
图 2 模型的解码过程 Fig. 2 Model decoding process |
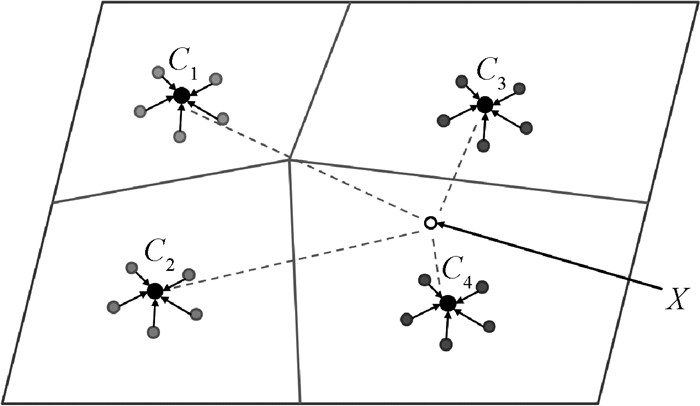
模型基分类器网络结构的搭建主要参考原型网络(prototypical networks)算法。在原型网络算法中会形成一个度量空间,在该度量空间中,每个类别都有一个特征原型,每个代表样本的特征点都要围绕在对应类别的原型周围形成一个聚类。为了达到这一目的,基分类器使用卷积神经网络来学习输入到度量空间中的非线性特征映射,并将支持集中每一类别特征映射的均值作为度量空间中每一类别的原型。然后,只需要对最近的类别原型进行查找,就可以对测试样本执行分类。图 3是在K-shot学习场景下模型基分类器的度量空间,图中K-shot学习基分类器计算支持集中每类样本嵌入特征的均值作为支持集的K-shot类别原型Ck,并将测试样本x的嵌入特征通过Softmax函数计算到类别原型进行分类,计算公式为
|
图 3 基分类器的度量空间 Fig. 3 Metric space of the base classifier |
| $ {p_\varphi }(\mathit{\boldsymbol{y}} = k\mid \mathit{\boldsymbol{x}}) \propto \exp \left( { - d\left( {{f_\varphi }(\mathit{\boldsymbol{x}}), {\mathit{\boldsymbol{C}}_k}} \right)} \right)。$ | (1) |
在K-shot学习基分类器中,给出一个支持集的n个有标签样本S={(x1, y1)(x2, y2), …, (xn, yn)},其中:xi∈RD是一个样本的D维特征向量;yi∈{1, 2,…, k}是对应的标签;Sk表示第k类标签的样本集合;fφ是具有可学习参数φ的特征提取函数。在计算过程中,基分类器通过具有可学习参数φ的特征提取函数fφ: RD→RM来计算支持集中每个类别的M维表示Ck∈RM,也就是每个类别的类别原型。在基分类器的度量空间中,每一类别的原型表示Ck是对支持集中的每一类别的所有样本的特征向量取均值得到的,所用公式为
| $ {\mathit{\boldsymbol{C}}_k} = \frac{1}{{\left| {{S_k}} \right|}}\sum\limits_{\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{y}}_i}} \right) \in {S_k}} {{f_\varphi }} \left( {{\mathit{\boldsymbol{x}}_i}} \right)。$ | (2) |
给定距离函数d: RM×RM→[0, +∞),K-shot学习基分类器会基于Softmax函数计算测试样本x到嵌入空间中类别原型的距离,并生成测试样本x在空间中的分布,而后通过随机梯度下降法将真实类别k的负对数概率J(φ)=-log pφ(y=kx)最小化,从而进行训练,所用公式为
| $ {p_\varphi }(\mathit{\boldsymbol{y}} = k\mid \mathit{\boldsymbol{x}}) = \frac{{\exp \left( { - d\left( {{f_\varphi }(\mathit{\boldsymbol{x}}), {\mathit{\boldsymbol{C}}_k}} \right)} \right)}}{{\sum\limits_{{k^\prime }} {\exp } \left( { - d\left( {{f_\varphi }(\mathit{\boldsymbol{x}}), {\mathit{\boldsymbol{C}}_{{k^\prime }}}} \right)} \right)}}{\rm{ }}。$ | (3) |
模型的基分类器由4个卷积块组成。每个卷积块都包含一个卷积层,其中,卷积层包含64个滤波器,每个滤波器的尺寸为3×3。一个ReLU激活函数、一个批量归一化层和一个步长为2的最大池化层。算法使用卷积神经网络提取训练样本的特征,并通过Adam的随机梯度下降进行训练。训练时,使用10-3的初始学习率,每1 000次训练将学习率减半,除了批量归一化外,不使用任何正则化。
3 实验与分析 3.1 数据集满文数据集中的所有数据是从《满语365句》一书中扫描得到,共计666个满文单词。根据《满语365句》的罗马转写字符用索贝特输入法录入了11种字体,并将每个满文单词的11种字体归为一类。小样本学习一般是指通过较大量的基类训练后,能够对只有少量有标签样本的新类进行识别的学习算法。因此在数据集的划分上,将数据集划分为支持集S、测试集Q、验证集V和辅助集A。其中支持集S和测试集Q由新类样本组成并一起构成一个小样本分类任务,如果S中包含C个类,每个类中又包含K个有标签样本,如K=5,将此类任务称为C-way K-shot任务。利用支持集S,即可对Q中每一个未标记的测试样本进行分类。辅助集A由基类样本组成并用于训练模型学习可转移的知识,辅助集A的类别空间与支持集S、测试集Q和验证集V都不相交。验证集V由新类样本组成并用于调整模型参数。在进行实验时,我们将原本的666类满文单词进行了划分,其中166类满文单词样本通过分别旋转90°、180°和270°的方式将原本的类别数扩充为4倍, 并作为基类进行辅助集A的构建。即辅助集A的类别数为166×4类,样本数为7 304个。剩下的500类样本作为新类构建了支持集S、测试集Q和验证集V,其中3个数据集共享相同的类别空间,将每个类别中的5个样本用于构建支持集S,4个样本用构建测试集Q,剩下的两个样本用于构建验证集V。支持集S、测试集Q和验证集V所包含的样本数分别为2 500、2 000和1 000。
3.2 实验结果与超参数分析我们选择最优的超参数进行对比实验,评价指标选择识别准确率,实验结果如表 2所示。本文模型的超参数设置如下:模型中N元ECOC编码矩阵中的N设置为50,也就是说对类别数量为200类、300类、400类和500类的支持集S都做了50元的分解,模型中的每个基分类器的分类类别数量也为50。基分类器数量设置为300,也就是说相应的预测编码长度为300,N元ECOC编码矩阵的列数L也为300。由表 2的数据可知,在大类别场景下,基于N元ECOC的K-shot学习模型拥有更高的识别准确率。在支持集类别增多的情况下,这些算法的识别能力普遍下降,但本文模型的降幅最小,相较于其他算法并不十分明显。
|
|
表 2 K-shot学习模型的识别准确率对比 Tab. 2 Comparison on recognition accuracy of K-shot learning models |
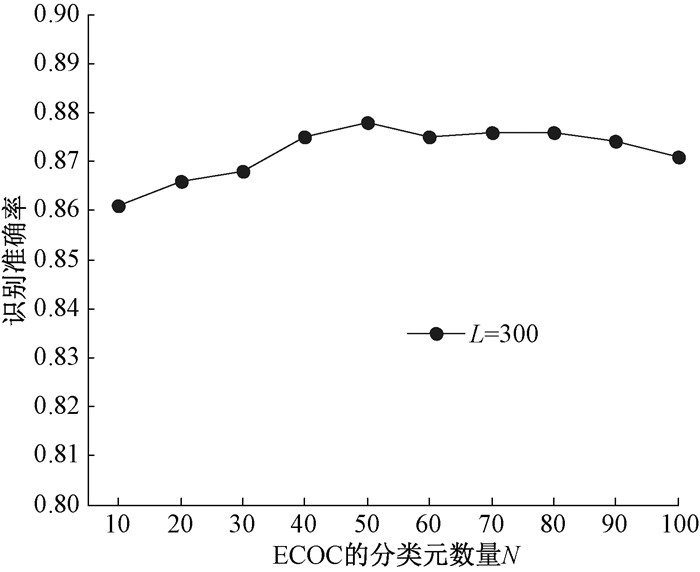
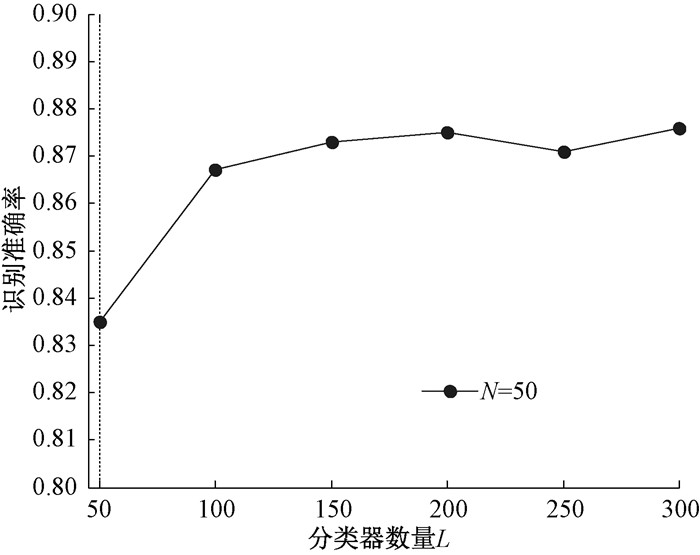
为了考察分解元的数量N和基分类器数量L对模型的识别准确率的影响,进而优化超参数的取值,我们进行了系列超参数灵敏度分析实验,结果如图 4和图 5所示。图 4的实验设置为满文数据集在500-way 5-shot的场景下,分类器数量为300。从图 4中可以看出,当N=50时,算法的识别准确率较高,因此在实验中选择N=50的分解。从图 5中可以看出,固定N的数量不变,随着基分类器数量的增加,模型识别准确率总体呈上升趋势,当K-shot学习基分类器的数量L=300时,模型即可实现较高精度的分类,分类准确率最终约为87.8%。
|
图 4 分类元数量N对模型识别准确率的影响 Fig. 4 Influence of parameter N on model recognition accuracy |
|
图 5 分类器数量L对模型识别准确率的影响 Fig. 5 Influence of the number of classifiers L on model recognition accuracy |
本文提出了一种适用于大类别分类场景的K-shot学习算法。核心思想是将大类别问题利用N元ECOC编码矩阵进行分解,得到一系列较小类别的分类问题, 再通过K-shot学习基分类器进行预测,最后对分类结果进行解码并输出。模型主要分为编码和解码两个部分。编码过程中利用N元ECOC编码对K-shot学习模型的支持集进行重新划分,划分后的子支持集类别变少,减小了基分类器的分类压力;解码阶段对由多个K-shot学习基分类器得到的预测编码利用N元ECOC编码矩阵解码,将与预测编码距离最近的类别编码作为最终分类结果,可以实现对识别错误的纠错,从而进一步提升了模型的识别准确率。在大类别满文数据集上进行的实验结果表明,本文提出的基于N元ECOC的K-shot学习算法在大类别场景下可以获得较高的识别准确率。
| [1] |
刘雪微, 王磊, 章强, 等. 基于卷积神经网络的多光谱掌纹识别技术[J]. 郑州大学学报(理学版), 2021, 53(3): 50-55. LIU X, WANG L, ZHANG Q, et al. Multi-spectral palmprint recognition technology based on convolutional neural network[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(3): 50-55. (  0) 0) |
| [2] |
HE K M, GKIOXARI G, DOLLAR P, et al. Mask R-CNN[J]. IEEE transactions on pattern analysis and machine intelligence, 2020, 42(2): 386-397. DOI:10.1109/TPAMI.2018.2844175 (  0) 0) |
| [3] |
毛晓波, 程志远, 周晓东. 基于特征图叠加的脱机手写体汉字识别[J]. 郑州大学学报(理学版), 2018, 50(3): 78-82. MAO X B, CHENG Z Y, ZHOU X D. Offline handwritten Chinese character recognition based on concatenated feature maps[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(3): 78-82. (  0) 0) |
| [4] |
LAI Y M, LI G M, WU D M, et al. 2019 novel coronavirus-infected pneumonia on CT: a feasibility study of few-shot learning for computerized diagnosis of emergency diseases[J]. IEEE access, 2020, 8: 194158-194165. DOI:10.1109/ACCESS.2020.3033069 (  0) 0) |
| [5] |
YAN L M, ZHENG Y H, CAO J. Few-shot learning for short text classification[J]. Multimedia tools and applications, 2018, 77(22): 29799-29810. DOI:10.1007/s11042-018-5772-4 (  0) 0) |
| [6] |
LI C, ZHANG D, TIAN Z Q, et al. Few-shot learning with deformable convolution for multiscale lesion detection in mammography[J]. Medical physics, 2020, 47(7): 2970-2985. DOI:10.1002/mp.14129 (  0) 0) |
| [7] |
KIM H U, KOH Y J, KIM C S. Online multiple object tracking based on open-set few-shot learning[J]. IEEE access, 2020, 8: 190312-190326. DOI:10.1109/ACCESS.2020.3032252 (  0) 0) |
| [8] |
HOWARD J, RUDER S. Universal language model fine-tuning for text classification[C]//Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). Melbourne: Association for Computational Linguistics, 2018: 328-339.
(  0) 0) |
| [9] |
NAKAMURA A, HARADA T. Revisiting fine-tuning for few-shot learning[EB/OL]. (2019-10-01)[2021-02-13]. https://arxiv.org/pdf/1910.00216.pdf.
(  0) 0) |
| [10] |
PISE N N, KULKARNI P. A survey of semi-supervised learning methods[C]//2008 International Conference on Computational Intelligence and Security. Suzhou: IEEE Press, 2008: 30-34.
(  0) 0) |
| [11] |
苏丰龙, 谢庆华, 黄清泉, 等. 基于直推式学习的半监督属性抽取[J]. 山东大学学报(理学版), 2016, 51(3): 111-115. SU F L, XIE Q H, HUANG Q Q, et al. Semi-supervised method for attribute extraction based on transductive learning[J]. Journal of Shandong university (natural science), 2016, 51(3): 111-115. (  0) 0) |
| [12] |
BONEY R, ILIN A. Semi-supervised few-shot learning with MAML[C]//6th International Conference on Learning Representations, ICLR 2018-Workshop Track Proceedings. Vancouver: International Conference on Learning Representations, 2018: 1-4.
(  0) 0) |
| [13] |
YOON J, KIM T, DiIA O, et al. Bayesian model-agnostic meta-learning[EB/OL](2018-11-19). http://arxiv.org/abs/1806.03836.
(  0) 0) |
| [14] |
LIU Y, LEE J, PARK M, et al. Learning to propagate labels: Transductive propagation network for few-shot learning[C]//7th International Conference on Learning Representations. New Orleans: International Conference on Learning Representations, 2019: 1-14.
(  0) 0) |
| [15] |
WANG Y X, GIRSHICK R, HEBERT M, et al. Low-shot learning from imaginary data[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington: IEEE Press, 2018: 7278-7286.
(  0) 0) |
| [16] |
MISHRA N, ROHANINEJAD M, CHEN X, et al. A simple neural attentive meta-learner[EB/OL]. (2017-01-11). https://arxiv.org/abs/1707.03141.
(  0) 0) |
| [17] |
MUNKHDALAI T, YU H. Meta networks[C]//34th International Conference on Machine Learning. Sydney: International Machine Learning Society, 2017(5): 3933-3943.
(  0) 0) |
| [18] |
RAVI S, LAROCHELLE H. Optimization as a model for few-shot learning[C]//5th International Conference on Learning Representations, ICLR 2017-Conference Track Proceedings. Toulon: International Conference on Learning Representations, 2017: 1-11.
(  0) 0) |
| [19] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016. ZHOU Z H. Machine learning[M]. Beijing: Tsinghua University Press, 2016. (  0) 0) |
| [20] |
SNELL J, SWERSKY K, ZEMEL R, et al. Prototypical networks for few-shot learning[C]//Advances in Neural Information Processing Systems 30-Proceedings of the 2017 Conference. Long Beach: Neural Information Processing Systems Foundation, 2017: 4078-4088.
(  0) 0) |
| [21] |
SUNG F, YANG Y X, ZHANG L, et al. Learning to compare: relation network for few-shot learning[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE Press, 2018: 1199-1208.
(  0) 0) |
| [22] |
VINYALS O, BLUNDELL C, LIFFICRAP T, et al. Matching Networks for One Shot Learning[C]//Advances in Neural Information Processing Systems 29-Proceedings of the 2016 Conference. Barcelona: Neural information processing systems foundation, 2016: 3637-3645.
(  0) 0) |
| [23] |
ZHOU J T, TSANG I W, HO S S, et al. N-ary decomposition for multi-class classification[J]. Machine learning, 2019, 108(5): 809-830. DOI:10.1007/s10994-019-05786-2 (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


