分布式电源(distributed generation, DG)具有发电方式灵活,节约投资和环保等优点而广泛被我国采用[1].目前,DG主要接入配电网运行,会对配电网造成多方面的影响, 如电能质量、安全和供电可靠性等[2-3].因此对这方面的研究会逐渐增多.
配电网中可能引起电压暂降的原因很多,如线路出现短路故障、电机启动和负荷容量变化等,其中造成最严重的电压暂降要属系统中的短路故障,其具有下降幅度大、波及范围广的特点[4],故障的地点和类型具有很强的随机性.如果合理分配分布式电源容量、并网位置和分布式电源的出力可以有效降低系统损耗,减少系统在故障发生时需要调节电压操作的次数[5];但是,对于辐射式电网,分布式电源并网将给系统带来如谐波污染、干扰保护装置动作等问题[6].目前,针对分布式电源的研究主要集中在电压控制和保护装置上,对电压暂降方面的研究并不多.
一般来说,电网中的监控设备能由监测数据来预估即将出现的电压暂降指标如幅值、持续时间等,如果要获得较高预测精度则所需的周期较长[7],多数情况下通过仿真预测来提高效率,因此本文将基于蒙特卡罗模拟原理对系统进行仿真.文献[8]提出了一种评估配电网电压暂降的算法,计算出故障时各节点可靠性概率指标.文献[9]主要采用蒙特卡罗方法研究中等规模的配电网,证明采用这种方法可以较准确反映系统的电压暂降状况.文献[10]采用时域仿真工具,设计一种随机预测电压暂降的程序,分析出电压暂降指数的重要性.
以上文献研究对象主要是针对出现电压暂降的原因和特点,对实际含分布式电源的配电网电压暂降情况没有做针对性研究.本文针对一个具体的辐射状电力系统(27节点的中压配电系统),应用蒙特卡罗模拟法的思想建立线路的故障概率模型,采用电磁暂态分析工具EMTDC/PSCAD进行仿真测试,利用大量仿真结果计算各节点电压暂降特征值,分析系统中由短路故障引起的电压暂降对敏感负荷节点造成的影响,并讨论当分布式电源接入后,在不同位置、出力和控制方式的情况下对各节点电压暂降的不同作用.
1 理论背景 1.1 分布式电源在本文的研究中均采用同步电机形式的DG,并且假设在电网出现故障时具备故障穿越能力.下面从位置、出力大小和控制方式3方面研究分布式电源在不同配置情况下对电压暂降的影响.
1) 位置.
位置因素主要包括DG的并网位置,敏感设备所在的母线编号.分为3种情形:
情形1: DG接在与敏感负荷相同馈线上且DG位于其上游节点;
情形2: DG接在与敏感负荷相同馈线上且DG位于其下游节点;
情形3: DG接在与敏感负荷不同的馈线上.
2) 出力大小.
分布式电源出力变化时会给系统注入不同的功率,因此注入功率变化会带来不同的电压暂降程度.分为2种情形:
情形1: DG出力对应负荷容量的30%;
情形2: DG出力对应负荷容量的50%.
3) 控制方式.
基于同步旋转电机形式的DG通常有两种控制方式:定电压控制方式和定功率因数控制方式.一般情况下,定功率因数控制方式应用较多.分为2种情形:
情形1:定电压控制,分别设定为V=1.0、1.05、0.95 p.u.;
情形2:定功率因数控制,分别设定为PF=1.0、0.95、0.85(滞后).
1.2 故障特征随机模型文中假设电压暂降都是因短路故障引起的.在对电压暂降进行概率评估将用到随机变量如故障类型FT、故障发生位置FLoc、各线路故障概率FL、故障持续时间FDur和故障阻抗FRes.
1) 故障类型.忽略故障接地电阻的作用,一共考虑4种故障类型:三相短路故障3L;两相短路2L;两相短路接地2LG;单相短路接地1LG.则随机数x在不同概率下的故障类型可表示为
| $ {F_{\rm{T}}}\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 1, \\ 2, \\ \vdots \\ 10, \end{array}&\begin{array}{l} x < {P_{3{\rm{L}}}}\\ {P_{{\rm{3L}}}} \le x < {P_{{\rm{3L}}}} + {P_{{\rm{AB}}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {P_{{\rm{3L}}}} + {P_{{\rm{AB}}}} + \cdots + {P_{{\rm{CG}}}} \le x \end{array} \end{array}} \right., $ |
式中:P3L~PCG为每种故障类型的概率,可从系统发生故障的历史数据获得;随机数x服从[0,1]的均匀分布.
2) 故障线路.在线路长度小于10 km的情况下,同一条线路上发生故障引起的负荷节点电压暂降程度相似.在本文仿真中可认为线路任意点发生故障的概率相同,因此故障概率可根据线路长度来计算,并用Li表示第i条线路的长度,m代表线路数,那么系统中第i条线路的故障概率为:
| $ {F_{\rm{L}}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 1, \\ 2, \\ \vdots \\ m, \end{array}&\begin{array}{l} y < {P_1}\\ {P_{\rm{1}}} \le y < {P_{\rm{1}}} + {P_{\rm{2}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {P_{\rm{1}}} + {P_2} + \cdots + {P_{m-1}} \le y \end{array} \end{array}} \right., $ |
式中:随机数y~U[0,1];Pm为系统中第m条线路发生故障的概率.
3) 故障位置.文中假设每条线路上各点发生故障的概率相同,因此服从均匀分布,即FLoc~U[0,1].
4) 故障阻抗.假定故障电阻服从期望为6 Ω,标准差为1 Ω的正态分布[11], 即FRes~N[6,1].
5) 故障持续时间.故障持续时间期望为0.06 s,标准差为0.01 s的正态分布, 即FDur~N[0.06, 0.01].
1.3 电压暂降指数电压暂降指数对评价一个系统的运行状态非常有用.在发生单次故障或连续多次故障时,通过仿真的方法不断更新电压暂降指数,从而能够有效反映出系统中部分节点或整个系统的特征[12].文献[13]提出了系统均方根值变化频率SARFIx来反映电压质量的可靠性,本文采用这一指数来评估电压暂降对系统造成的整体影响.定义SARFIx表达式如下:
已知有几种方法可用来仿真分析电网中引起的电压暂降现象,其中最常用的是故障点法和临界距离法[14-15].本文采用的是随机产生故障的方法.
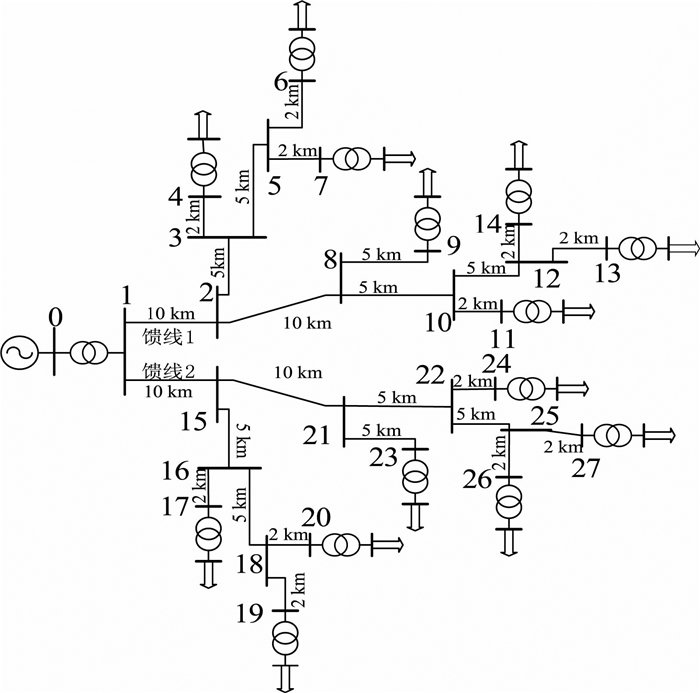
2.1 测试系统仿真采用的测试系统如图 1所示,可以看出此系统是一个辐射状含有2条馈线共27节点的中压配电网,其中变压器低压侧每相经过一个75 Ω的电阻接地.测试系统的基本参数为:
|
图 1 测试系统 Figure 1 Diagram of the test system |
电源等值模型:电压等级110 kV,额定容量1 500 MVA,X/R=10.
配电变压器参数:变比110/25 kV,额定容量20 MVA,短路电压百分比8%,Yd连接.
输电变压器参数:变比25/0.4 kV,额定容量1 MVA,短路电压百分比6%,Dy连接.
线路阻抗:Z1/2=0.61+j0.39 Ω/km,Z0=0.76+j1.56 Ω/km.
|
|
表 1 故障类型的比例 Table 1 Proportion of fault types |
基于蒙特卡罗模拟法的配电网电压暂降评估流程如下:建立含分布式电源的配电网电磁暂态模型.设定仿真次数m.由蒙特卡罗法特性知,仿真次数越多,其结果的误差越小,收敛性就越好.故障的概率信息由随机模型产生.仿真产生的随机数其实是伪随机数,但经过大量试验表明伪随机数能有效模拟实际情况.利用每次产生的随机数据进行仿真并记录其结果.重复以上步骤,直到给定仿真次数.仿真结束后对结果分析汇总并计算电压暂降的概率统计值,并据此得出电压暂降指标.图 2给出了评估电压暂降的流程图.

|
图 2 基于蒙特卡罗法的电压暂降评估流程 Figure 2 Flow chart of assessment on voltage sags based on Monte Carlo method |
电压暂降是由电力系统中的瞬时过程引起的,有多种类型的仿真工具可以模拟暂降过程,但只有时域仿真工具才可以高精度获取电压暂降的主要特征并评估其造成的影响.利用PSCAD/EMTDC仿真软件建立如图 1所示测试系统的模型,且负载均采用恒定阻抗,表示其负荷功率为常数.节点4、9、11、17、20和27为敏感负荷接入点.这里指出,在仿真中建立相应的元件和模块来实现特定的功能:
1) 依据概率密度方程产生随机变量的模块;
2) 可以将各种故障类型随机分布于线路中的三相传输线模块;
3) 监视并记录各个待分析节点数据的元件.
每次仿真结束,软件会输出每次反映故障特性的信息数据(如起始时间、持续时间、故障相、故障类型等)和反映电压暂降特性的信息数据(如残留电压、持续时间等).程序结束后,通过记录的信息来计算并获得暂降的概率密度方程以及平均每年发生的暂降次数.
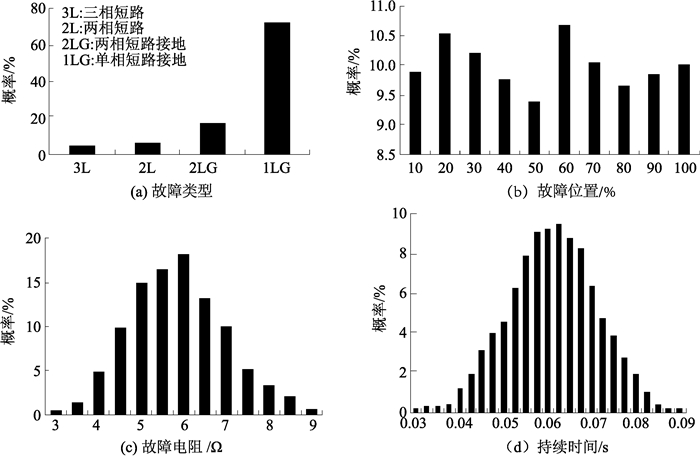
3.2 仿真结果及分析本文设定仿真次数m为2 000次.并假设平均每年在每100 km之间的架空线路一共出现12次短路故障,测试系统线路总长度为114 km,则2 000次仿真计算相当于模拟出系统共运行了146年的情况.根据仿真后的结果计算出各随机变量的概率分布如图 3所示.
|
图 3 随机变量概率分布 Figure 3 Distribution of random variables |
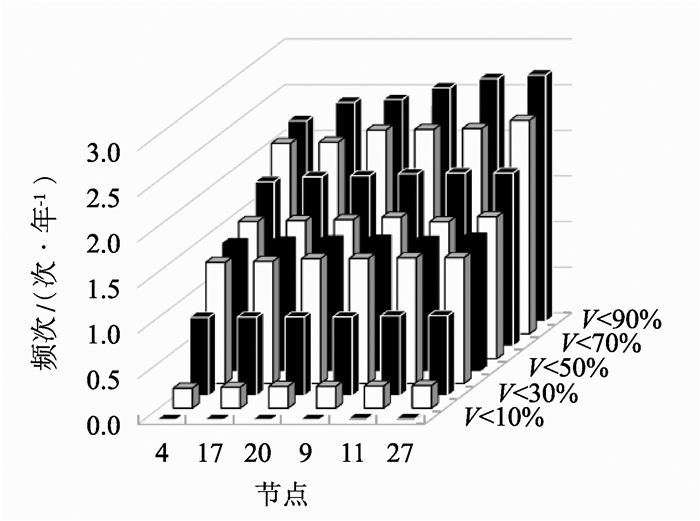
由图 3可知,在经过大量仿真并计算出的各随机变量概率分布与1.2节建立的随机模型相符.并得到各敏感负荷节点的SARFIx概率分布如图 4所示.
|
图 4 各敏感节点电压暂降概率分布 Figure 4 Probability distribution of voltage sag magnitude at sensitive nodes |
由图 4可知,对于相同节点,随着x取值变小,发生的电压暂降频次也就越少,电压减少的区间主要在额定值的30%~90%之间,电压低于20%以下的情况则相对少见.对于不同节点,在x取值一定时,发生的电压暂降频次差别不大,其大小由各节点与电源之间的电气距离决定,4、17、20节点距电源较近,9、11、27节点距电源较远,因此其SARFIx指数较大,在这些节点的负荷将承受更多次的电压暂降.
3.3 分布式电源对电压暂降的影响按照1.1节提供的各情形分析DG对电压暂降的影响,以节点9为对象,将DG分别接在节点2、节点13和节点21来作为3种不同的位置情形.表 2和表 3给出定电压控制方式和定功率因数控制方式下的SARFI70%指数.
|
|
表 2 定电压控制方式下SARFI70%指数 Table 2 SARFI70% indices under constant voltage control model |
|
|
表 3 定功率因数控制方式下SARFI70%指数 Table 3 SARFI70% indices under constant power factor control model |
由表 1和表 2,可以得出DG不同配置特性在评估电压暂降时所起的作用,并总结如下:
1) 位置.由上表结果可知,在前两种不同接入位置的情形下,DG接入可以有效缓解节点9出现的电压暂降频次,并且DG接在敏感负荷上游的效果要好于接在敏感负荷下游.对于第3种情形即DG与敏感负荷分别接在相邻的馈线,虽然能够起到降低电压暂降的作用,但这种效果不太显著.
2) 出力.无论DG在哪种控制方式下,改变其出力大小都能对电压暂降造成不同程度的影响,而且随着DG的出力从对应于总负荷的30%增大到50%,SARFI70%指数进一步降低.这是因为DG向系统提供了更多的无功功率.因此增大DG输出可以有效缓解电压暂降问题.
3) 控制方式.由数据可知,定电压控制和定功率因数控制产生的影响差别不大,对定电压控制,将端电压设为1.05 p.u.的结果要好于1.0 p.u.和0.95 p.u.,这是由于较高的端电压能够在故障发生期间内更好地支撑馈线电压.对于定功率因数控制,相对较低的功率因数如0.85将带来更好的结果,电压暂降频次低于功率因数为1和0.95的情形,因为功率因数越低,DG就能够提供更多无功功率来提高敏感负荷节点的电压.
4 结论本文以一个27节点的中压配电网为对象,应用蒙特卡罗模拟法对电压暂降进行研究,并且评估分布式电源接入后在3个不同的配置条件(不同位置、出力和控制方式)下对电压暂降造成的影响,得到以下结论:
1) 电压暂降造成严重的经济损失,因此通过电磁仿真工具来预测系统中可能出现的电压暂降,准确度高,适用性强,可为分布式电源接入优化提供依据.
2) 采用随机性预测的蒙特卡罗方法,建立其故障概率模型,可以用伪随机数来精确近似实际情况,有效解决电压暂降问题.
3) 文中采用电压暂降指数SARFIx来反映电压暂降情况,能够为电压暂降评估提供直观判据.
4) 同步电机型的DG接入系统后,经过3个方面的综合分析,得出如何合理利用分布式电源配置来有效缓解电压暂降.
| [1] |
易桂平, 胡仁杰. 分布式电源接入电网的电能质量问题研究综述[J]. 电网与清洁能源, 2015, 31(1): 38-46. (  0) 0) |
| [2] |
闫鼎. 分布式电源优化配置及其对电能质量的影响[D]. 上海: 上海交通大学, 2014. http://d.wanfangdata.com.cn/Thesis/D575959
(  0) 0) |
| [3] |
王鹤, 赵建军, 金一, 等. 基于逆变型分布式电源的电能质量管理研究[J]. 东北电力大学学报, 2014, 34(6): 86-90. (  0) 0) |
| [4] |
王宾, 潘贞存, 徐丙垠. 配电系统电压跌落问题的分析[J]. 电网技术, 2004, 28(2): 56-59. (  0) 0) |
| [5] |
JUAN A M, JACINTO M A. Impact of distributed generation on distribution protection and power quality [C]//IEEE Power & Energy Society General Meeting. Calgary, 2009:1-6.
(  0) 0) |
| [6] |
SURISUNTHON S, TAYJASANANT T. Impacts of distributed generation's locations, sizes, operation modes and transformer connections on voltage sag assessment [C]// IEEE Region 10 Conference. Indonesia, 2011:893-897.
(  0) 0) |
| [7] |
BOLLEN M H J. Understanding power quality problems:voltage sags and interruptions[M]. Hpboken: Wiley-IEEE Press, 2000.
(  0) 0) |
| [8] |
宋云亭, 郭永基, 张瑞华. 电压骤降和瞬时供电中断概率评估的蒙特卡罗仿真[J]. 电力系统自动化, 2003, 27(18): 47-51. DOI:10.3321/j.issn:1000-1026.2003.18.011 (  0) 0) |
| [9] |
杨京燕, 倪伟, 肖湘宁, 等. 计及电压暂降的配网可靠性评估[J]. 中国电机工程学报, 2005, 25(18): 28-33. DOI:10.3321/j.issn:0258-8013.2005.18.005 (  0) 0) |
| [10] |
JUAN A M, JACINTO M A. Voltage sag stochastic prediction using an electromagnetic transients program[J]. IEEE Trans on Power Delivery, 2004, 19(4): 1975-1982. DOI:10.1109/TPWRD.2004.829125 (  0) 0) |
| [11] |
邹禹平. 含分布式电源的配电网电压暂降凹陷域分析[D]. 山东: 山东大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10422-1014308139.htm
(  0) 0) |
| [12] |
代双寅, 韩民晓, 严稳莉. 含分布式电源的配电网电压暂降评估[J]. 电网技术, 2011, 35(7): 145-149. (  0) 0) |
| [13] |
MCDERMOTT T E, DUGAN R C, MCDERMOTT T E. PQ, reliability and DG[J]. IEEE industry applications magazine, 2003, 9(5): 17-23. DOI:10.1109/MIA.2003.1227867 (  0) 0) |
| [14] |
CHEN B, VUK M, DONG Y M, et al. Sensitivity analysis of voltage sag based fault location with distributed generation[J]. IEEE transactions on smart grid, 2015, 6(4): 2098-2106. DOI:10.1109/TSG.2014.2387153 (  0) 0) |
| [15] |
LI M, XIANG Y, COBBEN J F G. Voltage sag estimation based on probabilistic short circuit including the fault ride through effect of distributed generator[C]// International Conference on Power System Techndogy.Chengdu, 2014:2972-2979.
(  0) 0) |
| [16] |
GUPTA C P, JOVICA V M. Probabilistic assessment of equipment trips due to voltage sags[J]. IEEE Trans on Power Delivery, 2006, 21(2): 711-718. DOI:10.1109/TPWRD.2005.855447 (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


