2. 河北省数据驱动 工业智能工程研究中心 天津 300400;
3. 天津开发区精诺瀚海数据科技有限公司 天津 300400;
4. 天津光电通信技术有限公司 天津 300400;
5. 河北工业大学 材料科学与工程学院 天津 300400
2. Hebei Data Driven Industrial Intelligent Engineering Research Center, Tianjin 300400, China;
3. Tianjin Development Zone Jingnuo Data Technology Co. Ltd., Tianjin 300400, China;
4. TOEC Technology Co. Ltd., Tianjin 300400, China;
5. School of Materials Science and Engineering, Hebei University of Technology, Tianjin 300400, China
滚动轴承被广泛应用于飞机发动机、高铁滚轮、风力机等旋转机械中,其运行状态对整个机械的性能有着重要影响[1],因此判断轴承故障对保证旋转机械安全运行至关重要。
传统的轴承故障诊断方法主要是从信号的时域[2]、频域[3-4]和时频域[5]对故障原始振动信号进行分析和特征提取。但该类方法仍存在先验知识要求高、过度依赖复杂信号处理方法和诊断经验、浅层分类模型难以从少量特征中获取复杂的故障信息等问题。
深度神经网络能够有效提取振动信号深层次特征,具有不依赖先验信息和判别能力强的特点,很好解决了上述问题[6]。Khorram等[7]提出一种端对端的滚动轴承故障诊断算法,使用等效时间序列作为新型卷积长短记忆递归神经网络的输入,实现了短时间成本的故障诊断。Zhou等[8]提出一种改进的并行长短时记忆网络进行信号的特征提取,并将特征转换成图像,实现了利用卷积神经网络进行实时故障诊断。Zhang等[9]提出了一种将原始信号转换为二维图像,利用卷积神经网络进行特征提取和故障诊断的方法,并通过轴承数据验证了该方法的有效性。上述的深度学习方法相比于传统的基于信号分析的诊断方法,已经极大减少了对专家经验的依赖,但是此类方法大多直接从轴承故障原始时域振动信号中提取信息,存在故障诊断特征单一的问题。进而,有学者在多特征融合诊断方面进行了研究。如通过增加特征的维度进行诊断[10-12],但是此类方法仍然直接从轴承故障原始时域振动信号中提取信息,忽略了轴承故障在频域和时频域中的关键特征。
针对上述问题,提出一种基于权重自适应特征融合的轴承故障诊断方法(bearing fault diagnosis method based on adaptive weight feature fusion,BFD-AWFF),本文的主要贡献如下。
1) 针对滚动轴承原始时域信号中故障特征单一的问题,提出了双通道特征提取模型。对原始数据进行快速傅里叶变换和小波变换,突出原始信号中主要的故障特征,利用该模型实现对频域和时频域特征的提取。
2) 针对特征融合诊断时,关键故障特征重要程度缺失导致的模型收敛速度较慢问题,提出特征自适应加权算法,自适应地为频域和时频域特征匹配权重,提高模型收敛速度,实现故障诊断分类。
1 基于权重自适应特征融合的轴承故障诊断方法 1.1 方法框架传统轴承故障诊断研究中样本大多基于一维原始时域振动信号,存在诊断特征单一的问题,无法充分地利用振动信号中频域和时频域的差异性故障特征,导致故障诊断精度受限。本文提出的BFD-AWFF方法框架如图 1所示。

|
图 1 BFD-AWFF方法框架 Fig. 1 BFD-AWFF method framework |
该方法有特征提取模块和特征加权融合分类模块两个部分。特征提取模块中提出双通道特征提取模型,实现对故障的频域特征和时频域特征的提取;特征加权融合分类模块中提出特征自适应加权算法,实现对故障特征的加权融合。
1.2 特征提取模块由于传统的轴承故障诊断方法大多基于时域信号进行诊断,存在故障特征单一的问题,为了更好挖掘隐藏的多域故障信息,在特征提取模块中提出双通道特征提取模型,将经过时频分析之后的数据分别输入双通道中,得到故障的频域特征和时频域特征。双通道特征提取模型结构如图 2所示。
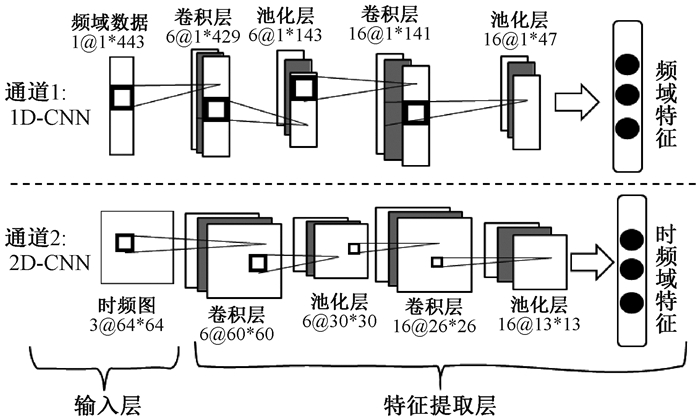
|
图 2 双通道特征提取模型 Fig. 2 Two-channel feature extraction model |
该模型由输入层和特征提取层组成。输入层包含通道1的一维卷积输入和通道2的二维卷积输入,分别接受一维频域数据和二维时频图作为输入数据;特征提取层的两个通道均由卷积、池化、激活函数和归一化相继堆叠组成,最后实现对故障的频域特征和时频域特征的提取。
1.2.1 输入层将传感器采集的原始轴承运转时的时序性信号按照统一步长进行分段切割数据,原始轴承振动信号序列数据可以表示为
| $ \boldsymbol{X}=\left[\boldsymbol{X}^{(1)}, \boldsymbol{X}^{(2)}, \cdots, \boldsymbol{X}^{(n-1)}, \boldsymbol{X}^{(n)}\right], $ | (1) |
其中:n为样本数量。截取每个时间点样本序列可以表示为
| $ \boldsymbol{X}^{(t)}=\left[x_1^{(t)}, x_2^{(t)}, \cdots, x_{d-1}^{(t)}, x_d^{(t)}\right], $ | (2) |
其中:t代表样本编号;d代表样本中的数据点数。
将时间点样本序列作为原始数据进行快速傅里叶变换之后可以得到变换之后的序列为
| $ \boldsymbol{X}_{\mathrm{fft}}^{\operatorname{input}(t)}=\left[x_1^{(t)}, x_2^{(t)}, \cdots, x_{k-1}^{(t)}, x_k^{(t)}\right], $ | (3) |
其中:k为原数据经过快速傅里叶变换之后的数据点数。将经过快速傅里叶变换之后的数据作为通道1的输入。
同时将时间段样本序列原始数据进行连续小波变换,变换之后形成的时频图如式(4)所示。小波变换时频图作为通道2的输入数据。
| $ \boldsymbol{X}_{\mathrm{cwt}}^{\operatorname{input}(t)}=\left[a_{n \times n}, b_{n \times n}, c_{n \times n}\right]。$ | (4) |
特征提取层分为两个通道,两个通道均由卷积、池化、激活函数以及归一化层循环堆叠而成。其中,通道1为一维卷积通道,输入为一维频域数据;通道2为二维卷积通道,输入为小波变换时频图。
卷积层可以通过设置卷积核的不同个数和大小实现对输入数据的差异性特征和上、下文信息的提取。其计算过程为
| $ \boldsymbol{c}^l=f\left(\boldsymbol{W} \cdot \boldsymbol{x}^l+\boldsymbol{b}\right), $ | (5) |
其中:xl代表输入向量;cl代表输出特征向量;W、b分别代表计算过程的权重和偏置向量,实现特征的非线性变换提取。
池化层的作用是降低特征向量的维度,从而降低卷积神经网络中需要计算的数据量,提升神经网络训练的效率。池化过程为
| $ \boldsymbol{P}^l=\max \left\{\boldsymbol{x}^l \mid s(m-1)+1 \leqslant n \leqslant s m\right\}, $ | (6) |
其中:max{·}代表最大池化策略;m、n为xl对应的pool核覆盖的区域;s为无重叠段长度;Pl表示池化后的特征矢量。
激活函数层采用ReLU函数作为激活函数,可以有效抑制梯度消失的问题,加快模型寻找全局最优解的过程,计算过程为
| $ \boldsymbol{R}^l=\boldsymbol{\varphi}\left(\max \left(\boldsymbol{x}^l, 0\right)\right)= \begin{cases}0, & \boldsymbol{x}^l \leqslant 0, \\ \boldsymbol{x}^l, & \boldsymbol{x}^l>0, \end{cases} $ | (7) |
其中:Rl表示激活后的特征矢量;φ(·)代表激活操作。
最后经过批归一化(BN)层,将隐含层中的输入变换标准正态分布,抑制了梯度消失和训练过程中的过拟合问题。
1.3 特征加权融合分类模块在特征融合过程中,传统方法大多使用Concatenate机制实现特征简单拼接融合,存在关键故障特征重要性缺失的问题,导致模型收敛速度变慢。针对上述问题提出特征自适应加权算法,该算法借鉴注意力机制,自适应地为频域和时频域特征匹配不同权重,实现高精度故障诊断分类,特征自适应加权融合过程如图 3所示。
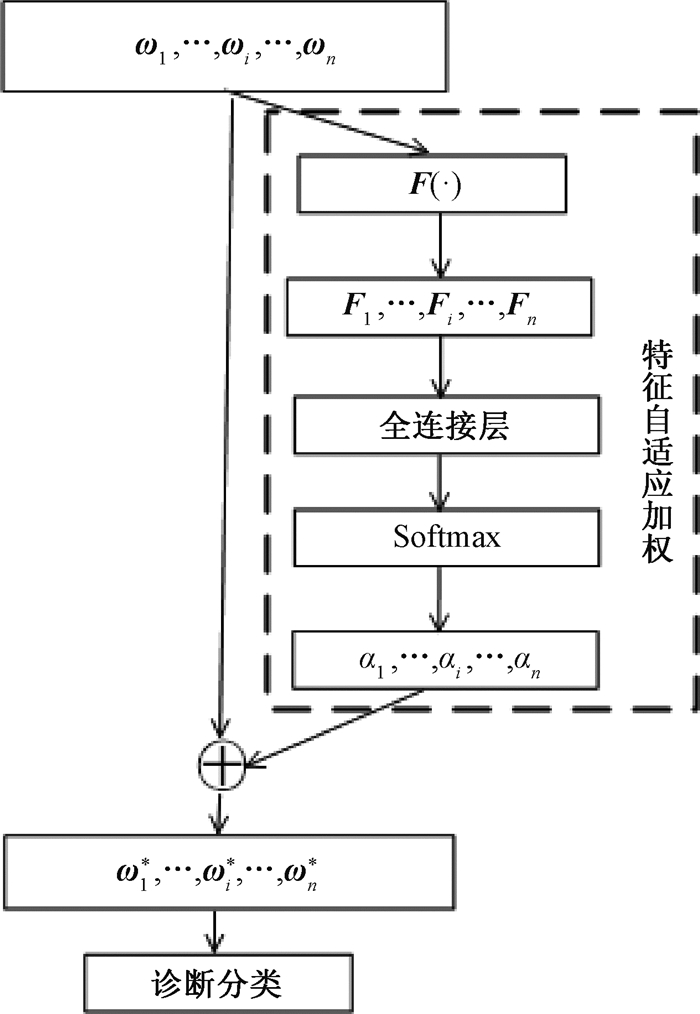
|
图 3 特征自适应加权融合算法 Fig. 3 Feature adaptive weighted fusion algorithm |
设特征提取模块的输出为ω1, …, ωi, …, ωn,其中:ωi为第i个特征提取通道的特征输出;ωi(k)为输出特征ωi的第k个数值;n为特征数量,由特征提取模块中的通道数决定。函数F(·)将第i个通道的输出特征ωi进行求和,得到相应的特征Fi,
| $ \boldsymbol{F}_i=\boldsymbol{F}\left(\boldsymbol{\omega}_i\right)=\sum\limits_{k=1}^m \boldsymbol{\omega}_i(k)。$ | (8) |
将获得的特征Fi通过全连接层获得输出φi,然后通过Softmax函数获得该特征的权重αi。αi为第i个特征提取通道所提取特征的权重,通过Softmax函数将每个通道所提取特征的权重映射到(0,1)数值空间,各通道特征的权重和为1,计算为
| $ {\alpha _i} = {\mathop{\rm Softmax}\nolimits} \left( {{\mathit{\boldsymbol{\varphi }}_i}} \right) = \frac{{{{\rm{e}}^{{\mathit{\boldsymbol{\varphi }}_i}}}}}{{\sum\limits_{k = 1}^n {{{\rm{e}}^{{\mathit{\boldsymbol{\varphi }}_k}}}} }}。$ | (9) |
加权之后的特征ωi*和融合特征F可表示为
| $ \boldsymbol{F}=\sum\limits_{i=1}^n \boldsymbol{\omega}_i^*=\sum\limits_{i=1}^n \alpha_i \cdot \boldsymbol{\omega}_{i }。$ | (10) |
将加权融合特征F作为故障诊断的依据,输入分类层进行故障分类。
分类层由3个全连接网络层组成,其中第一层全连接网络将加权之后的特征进行展平操作,即将所有加权特征矢量首尾连接组成一维向量;第二层全连接网络实现对融合之后的特征降维;第三层全连接网络的输出个数与故障类别数目保持一致,利用Softmax分类器实现目标输出类别。
2 实验及结果分析 2.1 实验数据集与实验平台本文采用美国凯斯西储大学(Case Western Reserve University,CWRU)电气工程实验室的轴承故障数据集[13]和德国帕德博恩大学(Paderborn University,PU)机械工程学院的轴承故障数据集[14]进行实验,验证本文方法的有效性。
CWRU轴承数据实验台使用电火花加工技术分别对置于驱动端和风扇段的轴承内圈(inner raceway,IR)、滚动体(ball,BO)和轴承外圈(outer raceway,OR)三个位置人为设置不同等级的单点故障,故障尺寸分别为0.1778mm、0.3556mm和0.5334mm。本文实验样本选取0 W下10种故障状态(包含一种正常状态)振动信号,CWRU数据集的具体实验样本信息如表 1所示。
|
|
表 1 CWRU轴承故障实验样本信息 Tab. 1 CWRU bearing fault test sample information |
PU数据集是一个6203轴承数据集,相比于CWRU数据集,该数据集的测试轴承故障既包含人工模拟损伤也包含真实损伤,本文选取的实验数据为真实损伤下的轴承数据,轴承故障分为单点损伤(single damage,S)和多点损伤(multiple damage,M)。故障发生的位置分为轴承的内圈(inner raceway,IR)和外圈(outer raceway,OR)。故障类型分为疲劳点蚀(fatigue pitting,FP)和压痕(indentation,IN)。选取其中的7种故障类别(包含一种正常轴承状态)数据进行实验,PU数据集的具体实验样本信息如表 2所示。
|
|
表 2 PU轴承故障实验样本信息 Tab. 2 PU bearing fault test sample information |
运行实验的计算机配置信息:CPU为Intel(R) Core(TM) i7-11800H;运行内存为DDR4 3200MHz 16GB;显卡为NVIDIA GeForce RTX 3060 6GB;编程语言为python3.7;深度学习框架为pytorch 1.10.1。
2.2 样本生成与时频分析对实验数据进行划分,每段数据样例长度为864,作为训练集、验证集以及测试集的原始样本数据,划分训练集、验证集和测试集的比例为7∶2∶1,每类故障样本生成数量为200。
将原始信号数据集随机划分为训练集、验证集和测试集之后,对数据集进行快速傅里叶变换[15]和小波变换[16],获取轴承故障原始振动信号中的频域和时频域特征。选择Cmor小波作为小波函数对轴承故障振动信号进行分析,可以更好地表征振动信号在时频域上的特征。
2.3 模型对比实验使用数据集验证BFD-AWFF方法在轴承故障诊断中的有效性。训练过程的超参数设置为:迭代次数为200;批次数据量为64;优化器选用Adam优化器;损失函数采用交叉熵损失函数(cross entropy loss)。构建6种模型进行对轴承故障诊断的对比实验,其中Model6为本文提出的模型,各个模型的结构及输入如表 3所示。
|
|
表 3 对比实验模型及输入数据 Tab. 3 Comparative experimental model and input data |
实验使用的性能指标准确率(accuracy)表示模型预测类别正确的样本数量占总样本数量的百分比。其中,训练集准确率(Train-acc)和验证集准确率(Valid-acc)为模型训练轮次200时的准确率。对比Train-acc和Valid-acc可以得到模型过拟合情况。测试集准确率(Test-acc)为训练完成的模型在测试集上的准确率,得到训练完成模型的效果。表 3中提到的6种模型的对比实验结果如表 4所示。
|
|
表 4 模型结果对比 Tab. 4 Comparison of model results |
由表 4可知,本文提出的方法在训练集、验证集以及测试集中都有最好的准确率。其中Model1、Model2和Model3为单通道模型,Model1的输入数据为原始振动数据,在训练集和验证集上的准确率有较大的差异,且在两个测试集上的Test-acc较低,分别为85.00%和84.28%;将原始振动数据经过快速傅里叶变换和小波变换之后,分别作为Model2和Model3的输入数据,Model2在两个测试集上的Test-acc分别达到了97.50%和96.42%,Model3在两个测试集上的Test-acc分别达到99.50%和95.71%,由此可以证明,快速傅里叶变换和小波变换对于提取原始数据中的故障特征均有较好的表现。Model4、Model5和Model6为双通道模型,Model6为本文方法,两个通道输入的数据分别为原始振动数据经过快速傅里叶变换之后的频域数据和小波变换之后的时频图,该模型在测试集的准确率最高,达到99.75%和98.57%。
本文所提方法在两个数据集上的训练曲线如图 4所示,其中图例标签“CWRU-train”表示该方法在CWRU数据集上的训练曲线,“CWRU-valid”表示该方法在CWRU数据集上的验证曲线;PU数据集同理。由该训练曲线可知,本文所提方法在训练过程中,模型具有较好的收敛性,且模型的收敛速度较快。证明本文所提方法可以有效提取轴承故障的频域特征和时频域特征,并对故障特征进行自适应加权融合诊断。
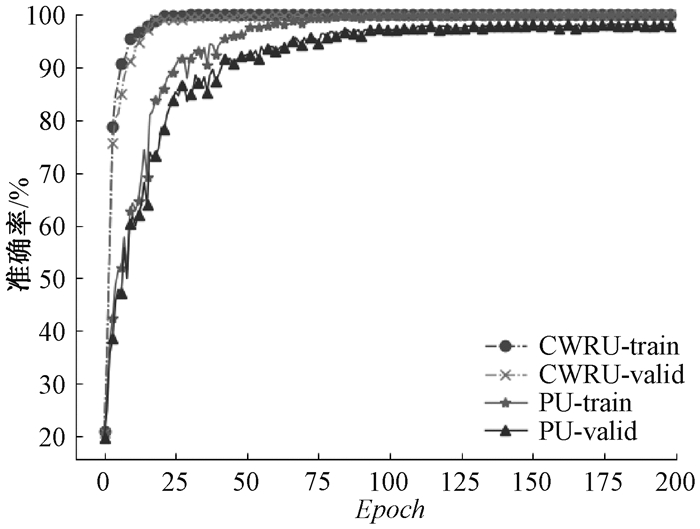
|
图 4 Model6在两个数据集上训练曲线 Fig. 4 Model6 training curve on two datasets |
为验证特征自适应加权模块在本文提出整体方法中的作用,对该模块进行消融实验。本节中的实验数据采用CWRU数据集和PU数据集,对本文提出的BFD-AWFF方法和无特征自适应加权的BFD-AWFF(BFD-AWFF with non feature adaptive weighting,BFD-AWFF-NA)方法进行对比实验,两个方法在两个数据集上的表现如表 5所示。
|
|
表 5 模型结果对比 Tab. 5 Comparison of model results |
由表 5可知,BFD-AWFF方法比缺少特征自适应加权的BFD-AWFF-NA方法在两个数据集上具有更高的分类准确率,在CWRU数据集上,虽然训练集和验证集准确率相同,但在测试集上有更高的准确率,提高了0.25%。在PU数据集上,训练集、验证集和测试集上的准确率,分别提高了3.67%、7.5%和3.57%。为了更好地说明特征自适应加权模块对模型训练过程中模型收敛速度的影响,将BFD-AWFF方法和BFD-AWFF-NA方法在两个数据集上的训练过程的准确率曲线进行对比,如图 5所示。
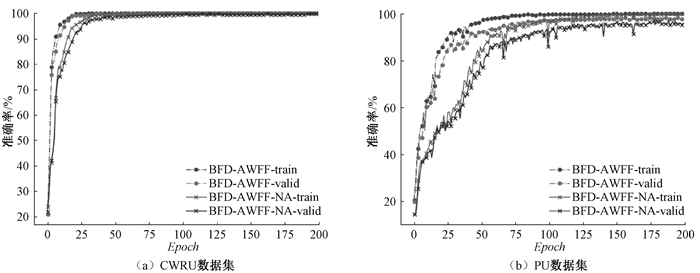
|
图 5 BFD-AWFF和BFD-AWFF-NA训练准确率与验证准确率曲线 Fig. 5 BFD-AWFF and BFD-AWFF-NA training accuracy and verification accuracy curve |
由图 5对比可知,在CWRU数据集上,添加特征自适应加权融合模块的BFD-AWFF在Epoch为20次后达到相对稳定,缺少特征自适应加权融合模块的BFD-AWFF-NA在Epoch为30次后达到较平稳状态;在PU数据集上,BFD-AWFF在Epoch为70次后达到相对稳定,BFD-AWFF-NA在Epoch为100次后达到较平稳状态。
经过对比实验,本文提出的BFD-AWFF方法通过在特征融合时加入特征自适应加权算法,使得该方法可以在两个数据集上具有最好的表现,且通过对关键特征赋予较高的权重,模型训练收敛速度明显提升。证明特征自适应加权算法针对特征提取模块提取的特征的重要程度高低赋予权重,实现故障特征有效融合从而加快模型收敛速度,提高故障诊断效果。
3 结论传统的轴承故障诊断方法大多基于原始时域信号进行特征提取,仅利用时域特征进行诊断,存在故障特征单一的问题。针对上述问题,提出一种基于权重自适应特征融合的轴承故障诊断方法(BFD-AWFF),该方法由特征提取和特征加权融合分类两个部分组成。在特征提取部分,提出双通道特征提取模型,对原始数据进行快速傅里叶变换和小波变换,并利用该模型对经过时频分析的数据同时提取故障的频域特征和时频域特征。在特征加权融合分类部分,使用特征自适应加权算法,实现特征动态自适应加权,加快模型收敛速度。通过CWRU数据集和PU数据集对BFD-AWFF方法进行实验验证,证明了该方法可以有效提取故障特征并保持优异的诊断准确率,同时证明特征自适应加权算法可以有效加快模型的收敛速度。
| [1] |
KANG M, KIM J, KIM J M. High-performance and energy-efficient fault diagnosis using effective envelope analysis and denoising on a general-purpose graphics processing unit[J]. IEEE transactions on power electronics, 2015, 30(5): 2763-2776. DOI:10.1109/TPEL.2014.2356207 (  0) 0) |
| [2] |
RAZAVI-FAR R, FARAJZADEH-ZANJANI M, SAIF M. An integrated class-imbalanced learning scheme for diagnosing bearing defects in induction motors[J]. IEEE transactions on industrial informatics, 2017, 13(6): 2758-2769. DOI:10.1109/TII.2017.2755064 (  0) 0) |
| [3] |
SONG L Y, WANG H Q, CHEN P. Vibration-based intelligent fault diagnosis for roller bearings in low-speed rotating machinery[J]. IEEE transactions on instrumentation and measurement, 2018, 67(8): 1887-1899. DOI:10.1109/TIM.2018.2806984 (  0) 0) |
| [4] |
ZHANG X, LIU Z W, WANG J X, et al. Time-frequency analysis for bearing fault diagnosis using multiple Q-factor Gabor wavelets[J]. ISA transactions, 2019, 87: 225-234. DOI:10.1016/j.isatra.2018.11.033 (  0) 0) |
| [5] |
王一宁, 甄成刚, 韩瑶瑶. 基于AFSA-PSO-LSSVM的风电机组齿轮箱故障诊断[J]. 郑州大学学报(理学版), 2022, 54(3): 81-87. WANG Y N, ZHEN C G, HAN Y Y. Fault diagnosis of gearbox of wind turbine based on AFSA-PSO-LSSVM[J]. Journal of Zhengzhou university (natural science edition), 2022, 54(3): 81-87. (  0) 0) |
| [6] |
刘晶, 高立超, 孙跃华, 等. 基于知识和数据融合驱动的设备故障诊断方法[J]. 郑州大学学报(理学版), 2022, 54(2): 39-46. LIU J, GAO L C, SUN Y H, et al. Fault diagnosis method for equipment driven by knowledge and data fusion[J]. Journal of Zhengzhou university (natural science edition), 2022, 54(2): 39-46. (  0) 0) |
| [7] |
KHORRAM A, KHALOOEI M, REZGHI M. End-to-end CNN+LSTM deep learning approach for bearing fault diagnosis[J]. Applied intelligence, 2021, 51(2): 736-751. DOI:10.1007/s10489-020-01859-1 (  0) 0) |
| [8] |
ZHOU F N, ZHANG Z Q, CHEN D M. Real-time fault diagnosis using deep fusion of features extracted by parallel long short-term memory with peephole and convolutional neural network[J]. Journal of systems and control engineering, 2021, 235(10): 1873-1897. (  0) 0) |
| [9] |
ZHANG J Q, SUN Y, GUO L, et al. A new bearing fault diagnosis method based on modified convolutional neural networks[J]. Chinese journal of aeronautics, 2020, 33(2): 439-447. DOI:10.1016/j.cja.2019.07.011 (  0) 0) |
| [10] |
吴静然, 丁恩杰, 崔冉, 等. 采用多尺度注意力机制的旋转机械故障诊断方法[J]. 西安交通大学学报, 2020, 54(2): 51-58. WU J R, DING E J, CUI R, et al. A diagnostic approach for rotating machinery using multi-scale feature attention mechanism[J]. Journal of Xi'an jiaotong university, 2020, 54(2): 51-58. (  0) 0) |
| [11] |
邓飞跃, 丁浩, 郝如江. 基于多尺度特征融合残差神经网络的旋转机械故障诊断[J]. 振动与冲击, 2021, 40(24): 22-28. DENG F Y, DING H, HAO R J. Fault diagnosis of rotating machinery based on residual neural network with multi-scale feature fusion[J]. Journal of vibration and shock, 2021, 40(24): 22-28. (  0) 0) |
| [12] |
张龙, 甄灿壮, 易剑昱, 等. 双通道特征融合CNN-GRU齿轮箱故障诊断[J]. 振动与冲击, 2021, 40(19): 239-245. ZHANG L, ZHEN C Z, YI J Y, et al. Dual-channel feature fusion CNN-GRU gearbox fault diagnosis[J]. Journal of vibration and shock, 2021, 40(19): 239-245. (  0) 0) |
| [13] |
LIU J. Helical fault diagnosis model based on data-driven incremental mergence[J]. Computers & industrial engineering, 2018, 125: 517-532. (  0) 0) |
| [14] |
LESSMEIER C, KIMOTHO J, ZIMMER D, et al. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: a benchmark data set for data-driven classification[C]//European Conference of the Prognostics and Health Management Society. Woodland Drive: PHM Society, 2018: 1-17.
(  0) 0) |
| [15] |
WANG X, MAO D X, LI X D. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network[J]. Measurement, 2021, 173: 108518. (  0) 0) |
| [16] |
SHENG Z P, XU Y G, ZHANG K, et al. Applications in bearing fault diagnosis of an improved Kurtogram algorithm based on flexible frequency slice wavelet transform filter bank[J]. Measurement, 2021, 174: 108975. (  0) 0) |
 2023, Vol. 55
2023, Vol. 55


