0 引言

在工程领域中，很多问题最终都可归结为求解大型线性方程组。由Sadd提出的GMRES(m)算法是求解大型线性方程组最有效的方法之一，被广泛应用到工程领域^[1-4]。随着GMRES(m)算法的广泛应用，为加快GMRES(m)算法的收敛速度，很多学者对该算法进行优化与改进，一种方法是采用预处理技术^[5-7]，通过加权技术，即WGMRES(m)算法来加快算法的收敛性。孙蕾等利用残量多项式预处理方法，建立右端多项式预处理GMRES(m)算法^[8]; 于春肖等通过深入探讨算法的收敛性与方程组系数矩阵的密切关系^[9], 提出一种预条件广义极小残余新算法; 杨圣炜等通过引用加权技术，提出了加权SGMRES算法(WSGMRES算法)^[10]; 在此基础上，仲红秀等利用加权策略和分析基底条件数，对块simple GMRES方法进行了改进，提出加权simple GMRES算法^[11]; Yu等通过改变m的取值来加快收敛，进而提出VRP-GMRES(m)算法^[12-13]; 郝雪景等利用截断技术，基于不完全正交的Arnoldi过程提出截断型变参数广义极小残余算法(VRP-IGMRES(m))^[14]。本文利用截断技术^[15-16]，提出一种不完全正交的WIGMRES(m)算法，并结合数值算例，分析该算法的高效性。

1 WGMRES(m)算法

考虑线性方程组Ax=b，其中，A为n阶非对称非奇异矩阵。取x₀∈Rⁿ为任一向量，令x=x₀+z，则方程组可化为Az=r₀，其中r₀=b-Ax₀。GMRES(m)算法是在Krylov子空间K_m=Span{r₀, Ar₀, …, A^m-1r₀}中寻求z_m且满足r_m=r₀-Az_m⊥AK_m，使得‖r_m‖=‖r₀-Az_m‖= $ \mathop {\min }\limits_{z \in {k_m}} $‖r₀-Az‖，并将x=x₀+z_m作为方程组的近似解。

定义1^[17]   设D=diag{d₁, d₂, …, d_n}，d_i>0，i=1, 2, …, n，称d_i为加权因子。取任意向量α, β∈Rⁿ，则它们的内积可简记为(α, β)_D=β^TDα= $ \sum\limits_{i = 1}^n d $_iα_iβ_i。相应的加权范数定义为‖α‖_D= $\sqrt {{{\left( {\boldsymbol{\alpha }, \boldsymbol{\alpha }} \right)}_D}} $=α^TDα, ∀α∈Rⁿ。

加权Arnoldi过程：

1) 取v₁=r₀/‖r₀‖_D;

2) 对于j=1, 2, …, m，计算$ {\boldsymbol{{\bar v}}}$_j+1=Av_j- $ \sum\limits_{i = 1}^j \boldsymbol{h} $_{i, j}v_i, h_{i, j}=(Av_j, v_i)_D, h_{j+1, j}=‖$ {\boldsymbol{{\bar v}}}$_j+1‖_D;

3) 若h_{j+1, j}=0, 则停止, 否则v_j+1=$ {\boldsymbol{{\bar v}}}$_j+1/h_{j+1, j}。

结合GMRES(m)算法和加权Arnoldi过程，WGMRES(m)算法计算步骤如下：

1) 选取x₀∈Rⁿ，m∈N⁺(m < n)，给定误差上界;

2) 选取d=(d₁, d₂, …, d_n)^T，使得‖d‖=$ \sqrt n $，计算r₀=b-Ax₀, β=‖r₀‖_D, v₁=r₀/β;

3) 执行加权Arnoldi过程，对于j=1, 2, …, m，计算h_{j+1, j}=‖$ {\boldsymbol{{\bar v}}}$_j+1‖_D, 若h_{j+1, j}=0，则转向步骤5)，否则计算v_j+1=$ {\boldsymbol{{\bar v}}}$_j+1/h_{j+1, j}，求解得{v_i}_i=1^m和H_m;

4) 求解最小二乘问题，$ \mathop {\min }\limits_{y \in {{\boldsymbol{\rm{R}}}^m}} $‖βe₁- H_my‖, 解得y_m，e₁=(1, 0, …, 0)^T∈R^m+1，记x_m=x₀+V_my_m;

5) 若‖r_m‖=‖r₀-Az_m‖ < ε，则x=x_m，迭代停止，否则x₀=x_m，转向步骤2)。

2 WIGMRES(m)算法

当m很大时，考虑到在构造krylov子空间的基向量和Hessenberg矩阵时要用到长递推公式，导致算法计算量和存储量过大，因此在WGMRES(m)算法的基础上进行改进，提出一种新型截断型算法，即WIGMRES(m)算法，该算法仅对Av_j前面的至多q个向量进行正交，v_j0, …, v_j，j₀=max{1, j-q-1}正交，其中q < m，令q₀=j₀=max{1, j-q-1}，称q₀为WIGMRES(m)算法的截断指标。算法具体步骤如下：

1) 选取x₀∈Rⁿ，m∈N⁺(m < n)，给定误差上界;

2) 选取d=(d₁, d₂, …, d_n)^T，使‖d‖=n，计算r₀=b-Ax₀, β=‖r₀‖_D, v₁=r₀/β;

3) 执行不完全正交的加权Arnoldi过程，计算h_ij=(Av_j, v_i)_D，j=1, 2, …, m，i=j₀, j₁, …, j，v_j+1=Av_j- $\sum\limits_{i = {j_0}}^j \boldsymbol{h} $_ijv_i，标准化h_{j+1, j}=‖ v_j+1‖_D，v_j+1=v_j+1/h_{j+1, j}，更新V_j+1与H_j，V_j+1=(V_j, v_j+1)，H_j= $\overline{\boldsymbol{H}}_{j}=\left(\begin{array}{cc} \overline{\boldsymbol{H}}_{j-1} & \boldsymbol{h}_{i j} \\ 0 & \boldsymbol{h}_{j+1, j} \end{array}\right)_{(j+1) \times j} $;其中, H_j为(j+1)×j的带状上Hessenberg矩阵，将上述迭代过程写成矩阵形式为

$ \boldsymbol{A} \boldsymbol{V}_{m}=\boldsymbol{V}_{m+1} \overline{\boldsymbol{H}}_{m} 。$

(1)

4) 求解最小二乘问题

$ \left\|\boldsymbol{r}_{m}\right\|=\min _{\boldsymbol{y} \in \bf{R}^{m}}\left\|\boldsymbol{\beta} \boldsymbol{e}_{1}-\overline{\boldsymbol{H}}_{m} \boldsymbol{y}_{m}\right\|，$

(2)

得y_m，其中e₁=(1, 0, …, 0)^T∈R^m+1;

5) 构造近似解，x_m=x₀+V_my_m;

6) 计算残余向量的模，‖r_m‖=‖b-Ax_m‖;

7) 重启动判断，若‖r_m‖ < ε，则精确解x=x_m，迭代停止; 否则，置x₀=x_m，m=m+1，转2)。

3 WIGMRES(m)算法的收敛性

为证明算法WIGMRES(m)的收敛性态，本文将WIGMRES(m)算法和WGMRES(m)算法联系起来，证明WIGMRES(m)的收敛性，为方便讨论，令WIGMRES(m)算法的残余向量的模为r_m(WIG), WGMRES(m)算法残余向量的模为r_m(WG)。

定理1   假设V_m+1列满秩，则WIGMRES(m)算法和WGMRES(m)算法在K_m(r₀, A)上的残值范数满足

$ \left\|\boldsymbol{r}_{m}(W I G)\right\| \leqslant S\left(\boldsymbol{V}_{m+1}\right)\left\|\boldsymbol{r}_{m}(W G)\right\|，$

其中：V_m+1由不完全正交化过程生成，S(V_m+1)=‖V_m+1‖‖V_m+1⁺‖，V_m+1⁺是V_m+1的广义逆。如果WIGMRES(m)算法在m步中断，即h_{m+1, m}=0。

证明   由r₀=βV_m+1e₁和式(1)可知，对应于r_m(WIG)的残值为r_m(WIG)=b-Ax_m(WIG)=V_m+1(βe₁- H_my_m)，因此

$ \left\|\boldsymbol{r}_{m}(W I G)\right\|=\left\|\boldsymbol{V}_{m+1}\left(\boldsymbol{\beta} \boldsymbol{e}_{1}-\overline{\boldsymbol{H}}_{m} \boldsymbol{y}_{m}\right)\right\|。$

(3)

由βV_m+1e₁=r₀，有βe₁=V_m+1⁺r₀，用V_m+1^H前乘式(1)可得H_m=V_m+1⁺AV_m。因此，式(3)变成‖r_m(WIG)‖=‖V_m+1(V_m+1⁺r₀-V_m+1⁺AV_my_m)‖。式(2)等价于求解最小二乘问题$ \mathop {\min }\limits_{y \in {{\boldsymbol{\rm{R}}}^m}} $‖V_m+1⁺r₀-V_m+1⁺AV_my_m)‖= $\min _{z_{m} \in K_{m}\left(\boldsymbol{r}_{0}, \boldsymbol{A}\right)} $‖V_m+1⁺r₀-V_m+1⁺Az_m)‖，因此可得

$ \left\|\boldsymbol{r}_{m}(W I G)\right\| \leqslant\left\|\boldsymbol{V}_{m+1}\right\|\left\|\boldsymbol{V}_{m+1}^{+} \boldsymbol{r}_{0}-\boldsymbol{V}_{m+1}^{+} \boldsymbol{A} \boldsymbol{V}_{m} \boldsymbol{y}_{m}\right\|=\left\|\boldsymbol{V}_{m+1}\right\| \min _{z_{m} \in K_{m}\left(r_{0}, A\right)}\left\|\boldsymbol{V}_{m+1}^{+} \boldsymbol{r}_{0}-\boldsymbol{V}_{m+1}^{+} \boldsymbol{A} \boldsymbol{z}_{m}\right\| \leqslant\\ \left\|\boldsymbol{V}_{m+1}\right\|\left\|\boldsymbol{V}_{m+1}^{+}\right\| \min _{z_{m} \in K_{m}\left(\boldsymbol{r}_{0}, \boldsymbol{A}\right)}\left\|\boldsymbol{r}_{0}-\boldsymbol{A} z_{m}\right\|=S\left(\boldsymbol{V}_{m+1}\right) \underset{z_{m} \in K_{m}\left(r_{0}, A\right)} \min\left\|\boldsymbol{r}_{0}-\boldsymbol{A} \boldsymbol{z}_{m}\right\|=S\left(\boldsymbol{V}_{m+1}\right)\left\|\boldsymbol{r}_{m}(W G)\right\|，$

证毕。

4 数值算例

算例1   考虑一维波动方程

$ \begin{cases}u_{t}=u_{x x}, & 0<x<1, 0<y<0.1, \\ u(0, y)=u(1, y)=0, & 0 \leqslant y \leqslant 0.1 \\ u(x, 0)=f(x)=\sin (\pi x)+\sin (3 \pi x), & 0 \leqslant x \leqslant 1_{\circ}\end{cases} $

(4)

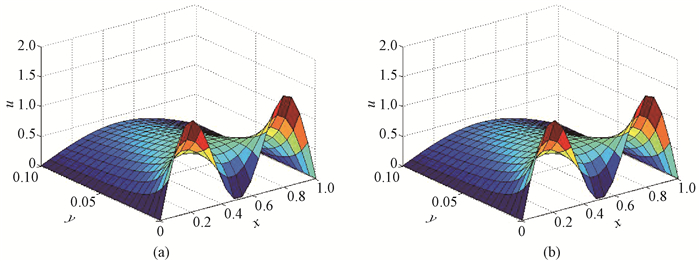
方程(4)的精确解为u(x, y)=sin(πx)e^-π2y+sin(3πx)e^-9π2y，如图 1(a)所示。将区域沿x方向和y方向n等分，其中采用隐式差分法求解方程(4)，可得方程组

$ u(x, y)=\sin (\pi x) \mathrm{e}^{-\pi^{2} y}+\sin (3 \pi x) \mathrm{e}^{-9 \pi^{2} y}。$

取n=20, m=10, q₀=9时，用WIGMRES(m)算法求解一维波动方程，计算结果如图 1(b)所示。由图 1知，问题(4)的数值解和精确解是一致的，说明WIGMRES(m)算法的正确性。

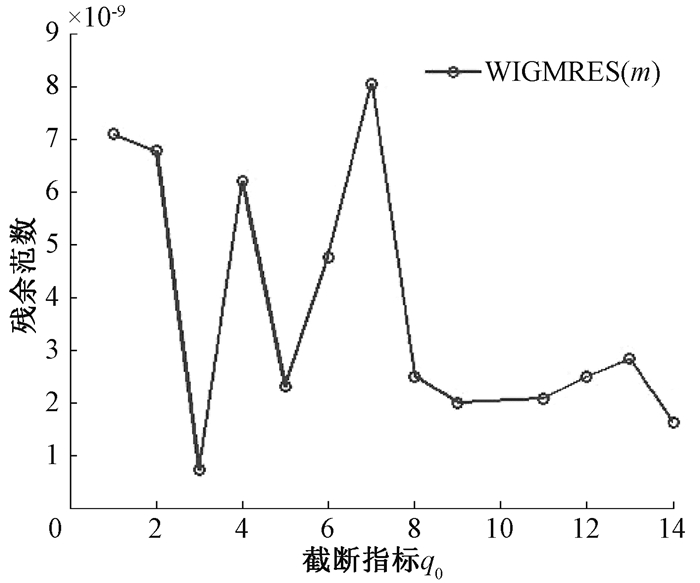
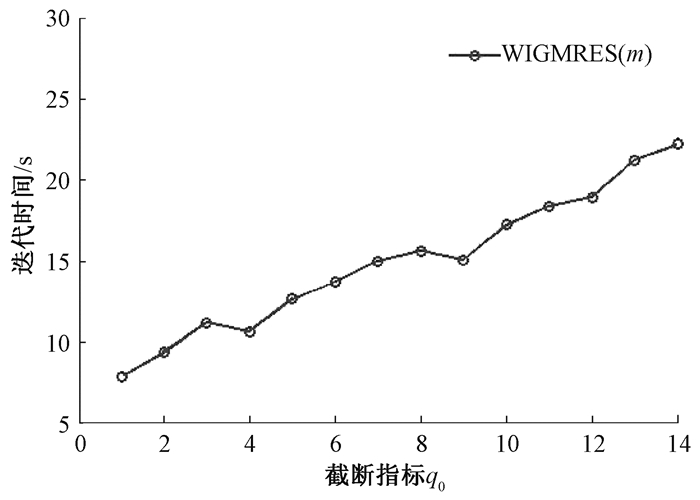
取n=30, m=15考虑截断指标q₀在1~14内取值，得到截断指标对残余范数和计算时间的图像如图 2、3所示，残余范数随着截断指标的增大波动后趋于平缓，计算时间随着截断指标的增大而缓慢增大，说明截断指标越小, 截断效果越明显。

算例2   考虑二维泊松方程

$ \begin{cases}-\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}\right)=2 \pi^{2} \sin \pi x \sin \pi y, & (x, y) \in {\mathit{\Omega}} \\ u(x, y)=\sin \pi x \sin \pi y, & (x, y) \in \partial {\mathit{\Omega}}\end{cases} $

(5)

其中：Ω={(x, y)0 < x, y < 1}，∂Ω为Ω的边界。

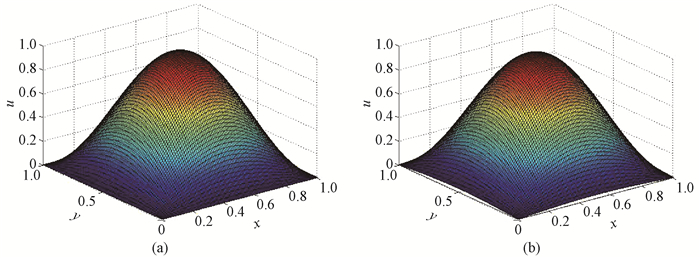
方程(5)的精确解为u(x, y)=sin πxsin πy，如图 4(a)所示。将区域沿x方向和y方向n等分，其中采用五点差分法求解方程(5)，可得方程组

$ \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}, \boldsymbol{A} \in \mathbf{R}^{(n-1)^{2} \times(n-1)^{2}}, \boldsymbol{x}, \boldsymbol{b} \in \mathbf{R}^{(n-1)^{2}}。$

取n=100, m=10截断指标q₀=9时，用WIGMRES(m)求解二维泊松方程的数值解如图 4(b)所示，根据图 4可知，数值解与精确解一致，因此说明算法WIGMRES(m)的正确性。

取n=50, q₀=5时，且m在4~14内取值，当重启动参数取不同的值时，GMRES(m)算法、WGMRES(m)算法和WIGMRES(m)算法的数值结果如表 1、2所示，当参数m发生变化时，GMRES(m)算法的迭代次数最多，WGMRES(m)算法次之，WIGMRES(m)算法最少且WIGMRES(m)算法的计算精度最高，由此证明WIGMRES(m)算法在保证精度的情况下计算效率大大提高。

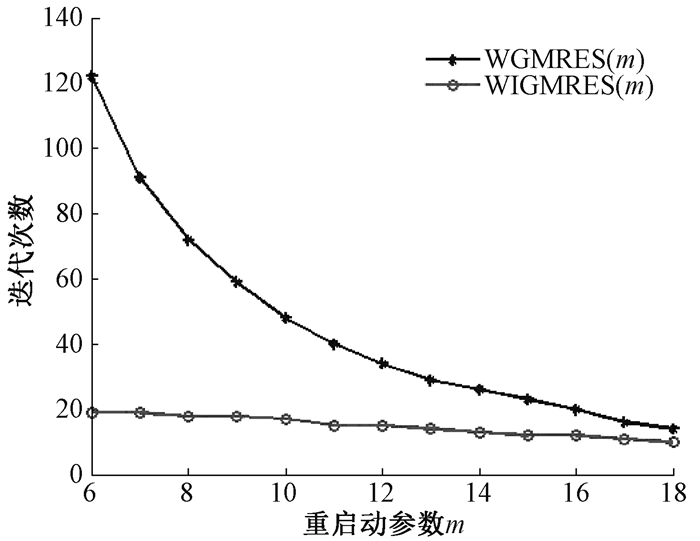
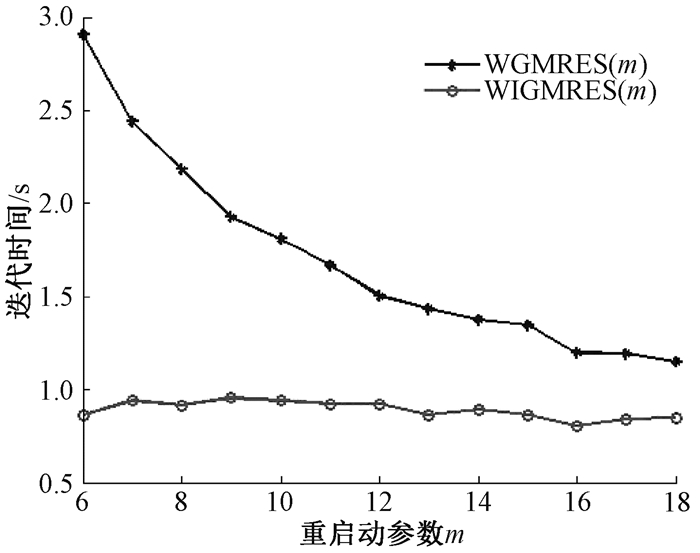
取n=40, q₀=5，且m在6~18内取值，执行WIGMRES(m)和WGMRES(m)两种算法，当重启动参数m取不同值，得到两种算法的迭代时间和迭代次数变化(图 5、6)。根据图 5、6可知，新算法WIGMRES(m)更加稳定，且以较高的精度快速收敛。当m=10时，不同网格下的两种算法的计算时间如表 3所示，表格显示随着n的不断增大，相同网格下，WIGMRES(m)算法总比WGMRES(m)算法的计算时间少，由此说明，WIGMRES(m)算法的优越性。

5 结论

本文在WGMRES(m)算法的基础上，通过采用截断技术，提出WIGMRES(m)新算法，并证明该算法的收敛性。通过数值算例证明WIGMRES(m)新算法得出的结果与精确解十分吻合，证明了该算法的有效性。同时当参数m取不同值时三种算法的迭代次数和计算精度的变化情况，以及WIGMRES(m)和WGMRES(m)两种算法对计算效率和计算精度的影响，结果表明新算法在计算效率和计算精度方面均有很大提高。