基于变量分组的大规模多目标优化算法

引用本文

林涛, 霍丽娜. 基于变量分组的大规模多目标优化算法[J]. 郑州大学学报(理学版), 2018, 50(4): 8-13.

LIN Tao, HUO Li'na. Based on Variable Grouping for Large-scale Many-objective Optimization Algorithm[J]. Journal of Zhengzhou University(Natural Science Edition), 2018, 50(4): 8-13.

基金项目

天津市自然科学基金重点项目(13jczdjc34400)

通信作者

作者简介

林涛(1970—)，男，天津人，教授，主要从事物联网技术与数据分析研究，E-mail:1965511415@qq.com;
霍丽娜(1992—)，女，河北保定人，硕士研究生，主要从事数据分析与智能算法研究，E-mail:huolina121@163.com

文章历史

收稿日期：2018-01-21

Contents Abstract Full text Figures/Tables PDF

基于变量分组的大规模多目标优化算法

林涛 , 霍丽娜

河北工业大学计算机科学与软件学院天津 300400

收稿日期：2018-01-21

基金项目：天津市自然科学基金重点项目(13jczdjc34400)

作者简介：林涛(1970—)，男，天津人，教授，主要从事物联网技术与数据分析研究，E-mail:1965511415@qq.com;
霍丽娜(1992—)，女，河北保定人，硕士研究生，主要从事数据分析与智能算法研究，E-mail:huolina121@163.com.

摘要：含有大规模决策变量的多目标优化问题，是当前多目标进化算法领域中的研究难点之一.针对此问题，提出一种基于变量分组的大规模多目标优化算法.该算法的贡献在于两个方面:1)提出一种新的决策变量分组方法，该方法通过随机采样与非支配排序，将决策变量分为收敛性变量和多样性变量；2)在种群进化过程中，采用levy分布函数产生新个体，同时设计出适应于此分布函数的优化过程.以反向世代距离(inverted generational distance, IGD)作为评价指标，在标准测试集函数上进行实验，实验结果证明该算法在解决大规模多目标优化问题时是有效的.

关键词：大规模多目标进化算法变量分组 levy分布

Based on Variable Grouping for Large-scale Many-objective Optimization Algorithm

LIN Tao , HUO Li'na

School of Computer Science and Engineering, Hebei University of Technology, Tianjin 300400, China

Abstract: In the field of many-objective evolutionary algorithm, the multi-objective optimization problem with large-scale decision variables was one of the difficult points. A large-scale many-objective optimization algorithm based on variable grouping was proposed. The contribution of the algorithm lied in the following two aspects. Firstly, a new method of the decision variables grouping was put forward. The decision variables were divided into convergence related and diversity related, through the sample randomly process and non-dominated sorting method. Secondly, in the process of population evolution, It was used the levy distribution function to generate new individuals, and designed the optimization process adapting to the distribution function. Inversed generational distance(IGD) as evaluation index, It was tested on standard test function DTLZ.Experimental results proved that, the algorithm was effective in solving large-scale many-objective optimization.

Key words: large scale many-objective evolutionary algorithm ovariable grouping levy distribution

0 引言

MOEA/D^[1]、NSGA-Ⅲ^[2]、GHEA2、IBEA等这些多目标进化算法在解决多目标优化问题时，大多关注目标数量增多时的性能，没有考虑含有大规模变量的情况，将决策变量当作整体优化，因此比较适合低维决策变量的多目标优化问题.文献[3-4]提出了一些大规模变量的单目标优化方法，但与多目标问题之间相互冲突，解决大规模变量的多目标优化问题更为复杂.文献[5]与文献[6]类似，采用决策变量随机分解策略，将大规模变量随机分组，然后融合合作协同框架^[7]与粒子群算法^[8]，进行优化，此算法易陷入局部最优，也没有提供一种降低分组变量之间依赖性的明确方法.在国外的文献中，2016年提出的MOEA/DVA^[9]算法，根据变量的控制属性将变量分为3类：多样性相关变量；收敛性相关变量；混合变量(两者都相关的变量).从而将大规模变量的多目标优化问题分解为多个简单的子多目标优化问题.但该算法不能处理混合变量过多的问题，并且算法只研究了目标数为2或3时的算法性能，对高维目标优化问题并不适用.受MOEA/DVA算法启发，文献[10]提出了LMEA算法，经过奇异值分解.计算角度、误差平方和等，基于聚类分析，首先将变量分为收敛性变量和多样性变量，然后再应用不同的优化策略分别优化.经实验验证，LMEA算法处理大规模变量多目标优化问题时，性能优于NSGA-Ⅲ等主流优化算法.但LMEA算法变量分组效果并不稳定且分解过程过于复杂.本文基于LMEA算法框架，首先提出了一种变量分解方法，不仅简化变量分解过程，并且提高变量分组准确率，然后在优化阶段采用levy变异策略产生子代，提高算法的全局寻优能力.

1 相关理论 1.1 变量相关性分析

相互独立的变量可以分开优化，各自的优化结果不会相互影响，相关变量因为它们之间的相关性，整体优化的结果可能与它们分开优化的结果不同，所以不能分开优化.设多目标优化问题min f(x)=(f₁(x)，f₂(x)，…，f_n(x))，如果存在决策向量x，实数a₁，a₂，b₁，b₂和至少一个目标函数f_k，1≤k≤n，使得f_k(x)|_{x_i=a₂，x_j=b₁} < f_k(x)|_{x_i=a₁，x_j=b₁}，f_k(x)|_{x_i=a₂，x_j=b₂}>f_k(x)|_{x_i=a₁，x_j=b₂}，那么决策变量x_i与x_j相关.

1.2 levy变异策略

levy变异^[11]能够产生更强烈的扰动作用，有助于提高算法的全局寻优能力.设种群规模为N，变量维度为D，其中个体x=(x₁，…，x_D)，经过levy变异产生的新个体设为x'=(x₁，…，x_D)，那么x与x'存在的关系为$ \left\{ \begin{array}{l} x{'_i} = {x_i} + {\delta _i} \cdot {L_i}\left( \beta \right), i = 1, 2, \cdots , D\\ {\delta _i} = \exp \left\{ {\tau N\left( {0, 1} \right) + \tau 'N\left( {0, 1} \right)} \right\} \end{array} \right.$, 其中：N(0, 1)是满足均值为0, 方差为1的正态分布；$\tau = 1/\sqrt N ;\tau ' = 1/\sqrt {2\sqrt N } ;{L_i}\left( \beta \right) $是满足levy分布的随机数，β=0.8.

2 基于变量分组的多目标优化算法(GLEA) 2.1 基于随机采样与非支配排序的大规模变量分组策略

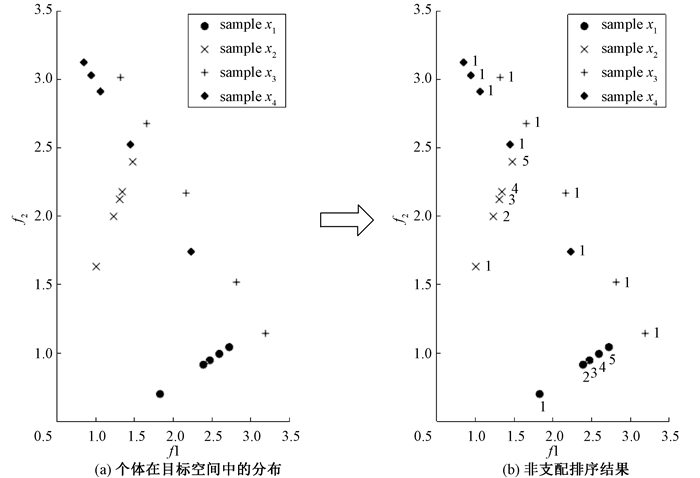
根据变量的控制属性，MOEA/DVA算法将大规模变量分为了3类：多样性变量；收敛性变量；混合变量.基于此，LMEA更细致地将变量分为收敛性变量和多样性变量.本文优化了LMEA算法的变量分解过程，通过对变量随机采样，根据对应目标空间的非支配排序结果，更简单精确地将变量分为收敛性变量和多样性变量.

设多目标优化问题为：$ \min \mathit{\boldsymbol{f}} = \min ({f_1}, {f_2});{f_1} = (1 + \sqrt {x_1^2 + x_2^2} )(2 - {x_3} - {x_4});{f_2} = (1 + \sqrt {x_1^2 + x_2^2} )$·(x₃+x₄); x_i∈[0, 1]，i=1，2，3，4.其中x₁、x₂、x₃、x₄为决策变量.4个变量分组过程为，对变量x₁，从种群中随机选择一个个体，对个体中的x₁随机采样5次，采样过程为在决策变量所在范围内，随机生成一个值，个体中的其他变量值保持不变，这样就得到一个拥有5个新个体的种群，在目标空间中对应的位置如图 1(a)中x₁所示，然后对5个个体进行非支配排序.x₂、x₃、x₄与x₁的处理过程相同，4个变量的非支配排序结果如图 1(b)所示.从图中可以看出，变量x₁、x₂非支配等级覆盖范围从1到5，个体朝最优解的方向收敛，变量表现为收敛性相关，而变量x₃、x₄对应的非支配等级只有1，没有收敛性，表现为多样性相关.于是根据非支配等级覆盖范围将变量分为了两组.

图 1 变量分组过程 Figure 1 The process of variable grouping

设个体为x=(x₁，…，x_D)，决策变量分组算法流程如下.

Step1：输入当前种群Pop，随机采样的次数nSample，初始化收敛性变量集合CV=∅，多样性变量集合DV=∅，i=1；

Step2：当i≤D时，执行以下步骤，否则算法结束，输出变量分组后的结果CV和DV集合；

Step3：从Pop中随机选择一个个体p₁；

Step4：对p₁中的变量x_i随机采样nSample次，形成一个种群SP；

Step5：对种群SP进行非支配排序，排序后的非支配序集合为{1，2，…，maxRankNo}；

Step6：如果maxRankNo>nSample/2，那么判定决策变量x_i是收敛性变量CV∪{x_i}，否则为多样性变量DV∪{x_i}；

Step7：i++，转到Step2.

其中，本文都采用T-ENS^[10]进行非支配排序.

2.2 基于levy变异的优化算法

将大规模变量分组后，对于收敛性变量和多样性变量两类变量，分别采用不同的优化策略.多样性变量集合中的变量同时优化，收敛性变量集合中的变量经过相关性分析后划分为多个子组，每个子组中的变量同时优化.

在多样性变量的优化策略中，对当前种群P通过levy变异操作得到第1代子种群，从第2代开始，将父代种群与子代种群合并，进行非支配排序分级，若前k个非支配层中的个体数量和大于P种群大小，那么前k-1非支配排序分级层中的个体直接作为下1代种群的一部分，另一部分从第k非支配层中选取，选取过程基于角度，首先计算第k非支配层中和已选中的个体在目标空间中的两两角度，记录每个第k非支配层中的个体与其他个体所成角度的最小角度，相继选择其中值最大的个体进入下1代种群.直到新的父代种群大小与原种群P大小相同.多样性变量的优化过程如下.

Step1：输入当前种群P，多样性变量集合DV，初始化下1代种群Q为空；

Step2：从种群|P|中随机选择P个个体{P₁，…，P_m，…，P_|p|}，对每个个体P_m(m=1，2，…，|P|)中的与多样性相关的变量值(即DV集合中指示的决策变量)，都通过levy分布产生一个新值，如此便得到|P|个新的个体，组成种群O；

Step3：将种群O与种群P合并，并进行非支配排序，得到f个非支配层，F_i表示第i个非支配层；

Step4：从非支配层的第1层开始累加，若第1层中的个体数量超过了P种群的个体数量，即|F_i|>P，那么首先选出F₁中的极值放入Q，F_k=F₁\Q; 若加到第k(k>1)层时，个体数量便超过了P种群数量，即|F₁|+…+|F_k|>|P|，|F₁|+…+|F_k-1|≤|P|, 那么将前k-1层的个体都放入种群Q；

Step5：在目标空间中计算Q∪F_k中的任何两个解的角度；

Step6:如果|Q| < |P|，执行Step7，否则输出新种群Q, 优化结束；

Step7：记录F_k中每个个体与Q中个体所成角度的最小角，并将F_k中的个体按照角度从大到小排序，从中选择最大角度的个体放入Q中，转到Step6.

优化收敛性变量，以相关性分析后生成的收敛性变量子组为单位，应用二元联赛法从当前种群中循环选择较优个体，以非支配序和目标空间个体到原点的距离分别作为第1和第2选择依据.通过levy变异策略产生子代，后代种群与父代种群合并，以距离和非支配序作为选择依据，从中选取较优个体生成下1代种群.收敛性变量的优化过程如下.

Step1：输入当前种群P、收敛性变量集合CV，经过相关性分析过程后生成的子组集合subCVs={group₁，group₂，…，group_n}，n表示子组的个数；

Step2：对种群P进行非支配排序；

Step3：在目标空间中计算种群P中每个个体到原点的距离；

Step4：i=1；

Step5：判断i是否小于n，如果i < n，执行后面步骤，否则输出优化后的种群P；

Step6：从种群P中，应用二元联赛法选择一个个体p₁，非支配排序和距离分别作为第1和第2选择依据，将p₁中对应集合group_i中指示的变量都通过levy分布产生1个新值，生成1个新的个体p'₁，重复此步骤，直到产生P个新个体，组成种群O；

Step7：将两个种群O与P合并，进行非支配排序；

Step8：计算两个种群中所有个体到原点的距离；

Step9：根据非支配排序等级和距离，用O中的解代替P中的解；

Step10：i++，转到Step5.

2.3 算法总体框架

GLEA算法主要分为4步：首先随机初始化规模为N的初始种群；然后将变量分组；再对收敛性变量集合进行相关性分析；最后分别优化多样性变量和收敛性变量，总流程如下.

Step1：输入种群规模N，随机采样次数nSample，相关性分析时选取的解的次数nCor，初始化种群P(N)；

Step2：执行变量分组过程，[DV，CV] ←VariableGroup(P，nSample)；

Step3：对Step2中输出的收敛性变量集合进行相关性分析，subCVs←InteractionAnalysis(P，CV，nCor)；

Step4：当不满足结束条件时，执行Step5，否则输出最终种群P；

Step5：执行多样性变量的优化过程，P←DiversityOptimization(P, DV)和收敛性变量的优化过程，P←ConvergenceOptimization(P, subCVs).

3 实验

本文采用测试集函数DTLZ系列作为测试函数^[12], 选择NSGA-Ⅲ、KnEA^[13]、MOEA/DVA、LMEA作为对比算法，算法的性能评价采用IGD^[14]指标.每个测试函数分别考虑5个和10个目标，分别取100、500、1 000个决策变量，每个算法独立运行20次，取平均值.得到表 1中对应的平均IGD指标值，表中加粗的数据是每个测试实例最好的结果.IGD指标计算公式为$ IGD(P, {P^*}) = (\mathop \sum \limits_{v \in {P^*}} d\left( {v, P} \right))/(|{P^*}|)$，其中：P是求解的最优Pareto前沿；P^*是真实的Pareto前沿，|P^*|值越大越能表示真实的Pareto前沿；d(v, P)是P^*中的个体v到P中所有个体的最小欧氏距离.本文采用文献[15]中的方法生成P^*中的个体.IGD值能够反映P相对P^*的多样性与收敛性，IGD值越小，说明P与P^*越相近，优化效果越好.

表 1 IGD值 Table 1 The value of IGD

测试函数	目标数	变量数	NSGA-Ⅲ	KnEA	MOEA/DVA	LMEA	GLEA
DTLZ1	5	100	3.934 0e+0(1.72e+0)	6.620 2e+0(1.83e+0)	6.293 2e-2(5.72e-5)	5.998 2e-2(4.22e-4)	6.587 4e-02(2.98e-03)
		500	5.259 7e+1(5.63e+0)	7.643 6e+1(6.86e+0)	6.328 4e-2(1.63e-4)	6.112 4e-2(5.16e-4)	6.674 5e-02(3.84e-03)
		1 000	1.166 9e+2(5.08e+0)	1.339 2e+2(1.28e+1)	6.344 2e-2(1.26e-4)	6.042 3e-2(4.09e-4)	6.510 2e-02(2.54e-03)
	10	100	1.194 4e+2(2.72e+1)	5.574 9e+0(1.53e+0)	1.435 6e-1(1.79e-2)	1.630 2e-1(4.87e-3)	1.294 5e-01(1.62e-02)
		500	3.982 9e+2(2.77e+1)	5.095 1e+1(1.25e+1)	1.704 7e-1(1.14e-2)	1.599 5e-1(4.05e-3)	1.313 6e-01(2.43e-02)
		1 000	7.984 1e+2(4.16e+1)	1.484 1e+2(1.93e+1)	1.380 5e-1(2.18e-2)	1.600 2e-1(5.24e-3)	1.278 4e-01(1.54e-02)
DTLZ2	5	100	1.949 4e-1(7.98e-7)	2.204 5e-1(1.18e-2)	1.949 3e-1(9.26e-8)	1.882 5e-1(2.14e-3)	1.895 4e-01(1.27e-03)
		500	1.949 4e-1(5.62e-8)	2.362 9e-1(7.63e-3)	1.949 4e-1(3.17e-8)	1.883 2e-1(2.29e-3)	1.894 0e-01(1.03e-03)
		1 000	1.949 4e-1(9.86e-7)	2.284 4e-1(1.00e-2)	1.949 4e-1(6.25e-8)	1.881 6e-1(2.53e-3)	1.894 4e-01(9.62e-04)
	10	100	4.214 1e-1(1.58e-4)	4.123 0e-1(2.24e-3)	4.592 3e-1(5.13e-2)	5.090 5e-1(1.48e-2)	4.015 8e-01(2.50e-03)
		500	4.215 2e-1(4.79e-5)	4.140 2e-1(5.07e-3)	4.197 6e-1(3.53e-4)	5.061 7e-1(1.78e-2)	4.019 3e-01(2.18e-03)
		1 000	4.217 2e-1(5.76e-5)	4.122 2e-1(1.85e-3)	4.206 5e-1(1.19e-4)	5.068 9e-1(2.84e-2)	4.026 2e-01(1.58e-03)
DTLZ3	5	100	2.286 8e+1(6.14e+0)	7.696 2e-1(4.18e-1)	1.950 5e-1(5.92e-5)	1.898 5e-1(2.14e-3)	1.941 7e-01(2.54e-03)
		500	2.942 1e+2(3.34e+1)	6.122 8e-1(1.26e-1)	1.953 6e-1(1.01e-4)	1.903 5e-1(4.44e-3)	1.938 4e-01(3.42e-03)
		1 000	6.822 9e+2(5.50e+1)	8.247 7e-1(2.42e-1)	1.956 3e-1(3.70e-4)	1.881 2e-1(4.10e-3)	1.944 5e-01(3.58e-03)
	10	100	8.219 3e+2(1.37e+2)	6.365 2e+0(3.88e+0)	5.074 7e-1(3.77e-2)	5.535 2e-1(3.56e-2)	4.381 9e-01(3.07e-02)
		500	2.289 1e+3(1.35e+2)	9.449 8e+0(4.57e+0)	5.282 0e-1(9.88e-2)	5.512 6e-1(1.66e-2)	4.424 8e-01(3.08e-02)
		1 000	4.407 1e+3(1.91e+2)	4.462 1e+0(2.34e+0)	4.772 8e-1(4.26e-2)	5.496 4e-1(1.85e-2)	4.640 5e-01(7.73e-02)
DTLZ4	5	100	2.729 8e-1(1.31e-1)	2.143 4e-1(4.33e-3)	2.695 7e-1(1.29e-1)	2.641 1e-1(1.55e-2)	1.920 9e-01(9.85e-04)
		500	1.949 6e-1(2.64e-5)	2.157 1e-1(9.97e-3)	3.442 1e-1(1.29e-1)	2.725 6e-1(2.46e-2)	1.918 5e-01(9.73e-04)
		1 000	2.282 9e-1(1.09e-1)	2.138 0e-1(4.21e-3)	3.442 0e-1(1.29e-1)	2.707 1e-1(2.36e-2)	1.925 1e-01(9.46e-04)
	10	100	4.212 3e-1(1.95e-4)	4.276 4e-1(2.53e-2)	4.377 2e-1(3.33e-2)	5.082 0e-1(2.47e-2)	3.905 0e-01(9.06e-04)
		500	4.215 4e-1(1.02e-4)	4.010 4e-1(4.57e-3)	4.197 0e-1(5.83e-5)	5.278 6e-1(3.98e-3)	3.905 1e-01(8.21e-04)
		1 000	4.217 3e-1(7.92e-5)	4.008 1e-1(2.61e-3)	4.569 5e-1(3.18e-2)	5.234 5e-1(9.26e-3)	3.903 1e-01(8.25e-04)
DTLZ5	5	100	1.495 7e-1(2.58e-2)	2.718 5e-1(4.11e-2)	2.044 0e-1(5.06e-4)	4.116 2e-3(1.44e-4)	3.210 2e-03(9.51e-07)
		500	1.941 3e-1(1.78e-2)	3.174 0e-1(6.11e-2)	2.046 9e-1(5.20e-8)	4.086 1e-3(1.48e-4)	3.210 4e-03(6.46e-07)
		1 000	2.060 6e-1(1.10e-2)	3.891 3e-1(6.77e-2)	2.046 1e-1(1.36e-4)	4.072 9e-3(9.90e-5)	3.210 8e-03(5.31e-07)
	10	100	3.194 6e-1(2.03e-2)	3.643 2e-1(5.71e-2)	1.887 7e-1(1.87e-4)	2.395 4e-3(6.95e-5)	1.478 9e-03(2.06e-07)
		500	5.264 2e-1(2.04e-2)	3.638 9e-1(5.43e-2)	1.886 6e-1(3.30e-4)	2.272 1e-3(4.47e-5)	1.479 0e-03(2.66e-07)
		1 000	6.209 3e-1(1.14e-2)	4.180 6e-1(5.07e-2)	1.888 0e-1(2.03e-4)	2.071 3e-3(6.98e-5)	1.479 1e-03(2.98e-07)
DTLZ6	5	100	2.564 2e-1(2.29e-2)	5.881 1e-1(1.34e-1)	1.823 6e-1(2.43e-6)	3.994 3e-3(2.14e-4)	3.210 5e-03(9.68e-07)
		500	4.993 9e-1(1.89e-2)	7.275 4e-1(1.43e-1)	1.823 6e-1(4.25e-7)	4.512 7e-3(1.22e-3)	3.210 7e-03(4.51e-07)
		1 000	6.577 4e-1(2.19e-2)	1.508 5e+0(4.53e-1)	1.823 6e-1(5.91e-7)	3.974 7e-3(2.29e-4)	3.210 6e-03(7.46e-07)
	10	100	7.212 0e+0(1.35e+0)	3.756 0e+0(9.56e-1)	1.653 1e-1(4.09e-2)	2.447 7e-3(5.11e-4)	1.478 8e-03(1.77e-07)
		500	8.717 1e+1(4.88e+0)	6.308 5e+0(2.18e+0)	1.275 0e-1(5.33e-2)	3.071 1e-3(7.20e-4)	1.478 8e-03(2.37e-07)
		1 000	1.920 2e+2(9.83e+0)	4.898 9e+0(2.54e+0)	1.184 4e-1(2.26e-2)	3.707 7e-3(1.66e-3)	1.478 8e-03(2.32e-07)
DTLZ7	5	100	5.284 9e-1(1.56e-1)	2.479 0e-1(1.14e-2)	5.204 4e-1(2.51e-6)	3.091 3e-1(1.10e-2)	3.423 1e-01(7.62e-03)
		500	2.392 8e+0(1.60e-1)	2.319 1e-1(7.58e-3)	5.204 3e-1(4.57e-7)	3.203 2e-1(8.53e-3)	3.429 6e-01(8.82e-03)
		1 000	2.663 3e+0(1.38e-1)	2.340 8e-1(1.44e-2)	5.204 3e-1(7.54e-7)	3.105 1e-1(7.59e-3)	3.449 0e-01(1.22e-02)
	10	100	4.668 4e+0(4.21e-1)	1.385 4e+0(3.48e-2)	1.638 5e+0(7.84e-2)	1.074 9e+0(6.40e-3)	1.085 6e+00(1.79e-02)
		500	1.187 5e+1(8.36e-1)	1.357 2e+0(1.65e-2)	1.632 0e+0(1.02e-1)	1.075 2e+0(3.29e-3)	1.089 1e+00(1.55e-02)
		1 000	1.502 7e+1(9.39e-1)	1.330 0e+0(9.50e-3)	1.524 9e+0(4.16e-2)	1.078 1e+0(4.58e-3)	1.086 8e+00(1.60e-02)

表 1 IGD值 Table 1 The value of IGD

3.1 参数设置

模拟二项式交叉、多项式变异的分布指数设为20, 交叉与变异概率分别设为P_c=1.0, P_m=1/D, D表示变量维度；在目标数为5时，种群规模设为126，NSGA-Ⅲ算法中帕累托前沿的边界层和内层参考点的数量分别设为5和0；目标数为10时，种群规模设为275，NSGA-Ⅲ算法中帕累托前沿的边界层和内层参考点的数量分别设为3和2；算法的终止为，100维决策变量时，最大评价次数设为1.0e+6；500维决策变量时，最大评价次数设为6.8e+6；1 000维决策变量时，最大评价次数设为1.7e+7；在KnEA算法中控制Knee points比率的参数T，5个目标时，DTLZ1、DTLZ3设置为0.3，10个目标时设置为0.1.5个目标时，DTLZ5、DTLZ6设置为0.4，10个目标时设置为0.3.DTLZ2、DTLZ4、DTLZ7在5个、10个目标时都设置为0.5.MOEA/DVA算法相关性分析的数量和控制属性分析的数量分别设置为NIA=6、NCA=50.LMEA算法在变量分组过程选择的解的数量nSel=2, 随机采样的次数nPer=4；相关性分析过程选择解的数量nCor=6.

3.2 实验结果

如表 1所示，表中加粗的数据是每个测试实例最好的结果.总体来看，LMEA与GLEA算法相对于NSGA-Ⅲ与KnEA、MOEA/DVA算法在大规模多目标问题上性能良好，并且IGD结果相近，LMEA与GLEA随着变量维度增大，性能表现一致，具有良好的伸缩性.GLEA在DTLZ1到DTLZ6测试函数为10个目标时，在几个算法中都是较优的；在DTLZ4、DTLZ5、DTLZ6测试函数上，GLEA不论5个目标还是10个目标时，表现较优；对于DTLZ7测试函数，10个目标时LMEA与GLEA算法结果基本相等，GLEA算法稍逊于LMEA.从IGD测试指标可以看出，对比其他几个多目标算法，GLEA在解决大规模多目标问题时是有效的.

4 总结

本文提出的GLEA算法，在变量分解过程中，根据变量的控制属性，通过扰动变量和非支配排序，将大规模决策变量简单精确地分为两类，在进化过程中，采用levy变异策略产生子代，提高算法的全局寻优能力.在标准测试函数DTLZ系列进行仿真实验，用IGD指标进行性能评价，实验结果表明：GLEA比NSGA-Ⅲ、KnEA、MOEA/DVA性能提升显著.当目标数分别增加到5个、10个超多目标，决策变量分别增加到100维、500维、1 000维大规模的决策变量时，GLEA能够更好地保持解的多样性与收敛性.对比LMEA算法，GLEA整体稍好于LMEA.GLEA能够较好地解决大规模决策变量的多目标优化问题.

参考文献

[1]	ZHANG Q, LI H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 (0)
[2]	DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part ⅰ: solving problems with box constraints[J]. IEEE transactions on evolutionary computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 (0)
[3]	CHENG R, JIN Y. A competitive swarm optimizer for large scale optimization[J]. IEEE transactions on cybernetics, 2015, 45(2): 191-204. DOI:10.1109/TCYB.2014.2322602 (0)
[4]	CHENG R, JIN Y. A social learning particle swarm optimization algorithm for scalable optimization[J]. Information sciences, 2015, 291(6): 43-60. (0)
[5]	邱飞岳, 莫雷平, 江波, 等. 基于大规模变量分解的多目标粒子群优化算法研究[J]. 计算机学报, 2016, 39(12): 2598-2613. DOI:10.11897/SP.J.1016.2016.02598 (0)
[6]	邱飞岳, 莫雷平, 王丽萍, 等. 周期性变量分解的多目标进化算法研究[J]. 小型微型计算机系统, 2016, 37(6): 1318-1322. DOI:10.3969/j.issn.1000-1220.2016.06.039 (0)
[7]	POTTER M A, JONG K A D. A cooperative coevolutionary approach to function optimization[M]. Berlin: Springer-Verlag, 1994: 249-257. (0)
[8]	王杰, 李慧慧, 彭金柱. 一种拟随机初始化模拟退火粒子群算法[J]. 郑州大学学报(理学版), 2016, 48(3): 75-81. (0)
[9]	MA X, LIU F, QI Y, et al. A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with large-scale variables[J]. IEEE transactions on evolutionary computation, 2016, 20(2): 275-298. DOI:10.1109/TEVC.2015.2455812 (0)
[10]	ZHANG X Y, TIAN Y, CHENG R, et al. A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization[J]. IEEE transactions on evolutionary computation, 2018, 22(1): 97-112. (0)
[11]	董红斌, 黄厚宽, 何军, 等. 一种求解约束优化问题的演化规划算法[J]. 计算机研究与发展, 2006(5): 841-850. (0)
[12]	DEB K, THIELE L, LAUMANNS M, et al. Scalable test problems for evolutionary multiobjective optimization[M]. London: Springer-Verlag, 2005: 105-145. (0)
[13]	ZHANG X Y, TIAN Y, JIN Y. A knee point-driven evolutionary algorithm for many-objective optimization[J]. IEEE transactions on evolutionary computation, 2015, 19(6): 761-776. DOI:10.1109/TEVC.2014.2378512 (0)
[14]	ZHOU A, JIN Y, ZHANG Q, et al. Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Vancouver, 2006: 892-899. (0)
[15]	DAS I, DENNIS J E. Normal-boundary intersection: a new method for generating the pareto surface in nonlinear multicriteria optimization problems[J]. Siam journal on optimization, 1998, 8(3): 631-657. DOI:10.1137/S1052623496307510 (0)