移动机器人在工业、农业、航空航天、医疗、服务等领域的应用越来越广泛。路径规划对提高移动机器人运动的准确性和运行效率起着关键作用,已经成为相关研究领域中的重要课题[1]。移动机器人路径规划是在有障碍物的环境中从起点到目标点规划出一条无碰撞路径。路径规划包括工作空间建模和最优路径规划。常用的工作空间建模方法有栅格法、几何空间法、拓扑法等[2]。栅格法和几何空间法不能有效地表达环境的复杂性。拓扑法可以表述全局环境的连通性,最具代表性的是MAKLINK图。常用的路径规划方法有Dijkstra算法[3]、A*搜索算法[4]、快速搜索随机树法(RRT)[5]、粒子群优化(PSO)算法[6]等。PSO算法是模拟鸟群飞行觅食行为的群智能搜索算法,具有易实现、精度高、收敛快等特点[7],但也存在算法易陷入早熟收敛问题。针对这个问题,文献[8]将遗传算法和随机编码的交叉算子(RCPSO)引入PSO算法中;文献[9]提出了基于跳出机制和牵引操作的粒子群优化(JMPOPSO)算法;文献[10]提出了加速收敛的粒子群优化(ACPSO)算法,使粒子从本地最小的吸引力区域逃脱。此外,文献[11]通过采用动态分组的粒子群(DGPSO)优化机制,提高了路径搜索的安全性和实时性。
本文针对基本粒子群优化(basic particle swarm optimization, BPSO)算法易陷入局部最优、规划路径较长等问题,提出了优于平均适应度值的改进粒子群优化(superior average particle swarm optimization, SAPSO)算法,该算法中粒子的更新速度是向适应度值优于平均适应度值的粒子学习,并对低于平均适应度值的粒子进行变异处理。仿真结果表明该方法提高了粒子的多样性,并且规划的路径最短。
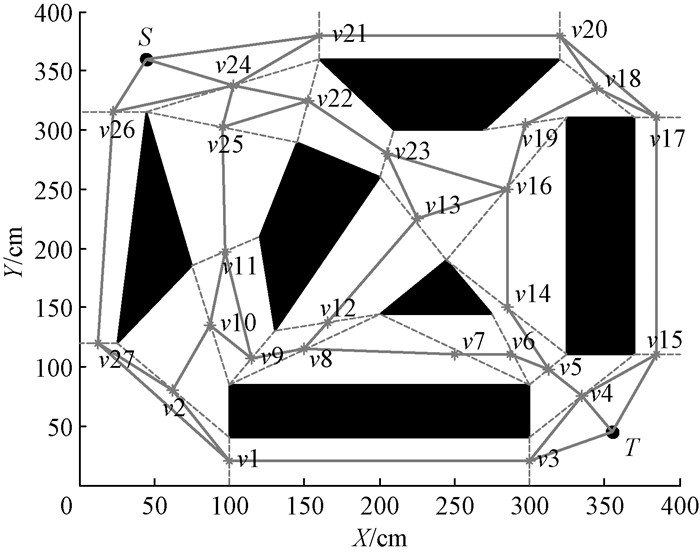
1 工作空间建模和次优路径规划 1.1 移动机器人工作空间建模移动机器人工作在400 cm*400 cm的室内环境中,空间分布着不同形状的障碍物,障碍物形状、位置等信息已知,采用MAKLINK图建立移动机器人工作空间的障碍物顶点模型。为了实现基于PSO算法的移动机器人路径规划,给出以下假设:①移动机器人的运动空间中分布着有限个已知的障碍物,并且障碍物的高平行于Z轴,即可以忽略障碍物的高度信息,只用(X, Y)平面进行描述;②为保证路径不太接近障碍物,把障碍物的边界扩展为机器人本体在长、宽方向上最大尺寸的一半,此时机器人可当作质点,且尺寸大小忽略不计。基于以上假设,使用MAKLINK图建立机器人的工作空间模型,得到如图 1所示的机器人运动空间链路图。图 1中的多边形是工作环境中的静态障碍物,S为起始点,T为目标点,虚线是障碍物的自由链接,实线是构成无碰撞路径网络的自由链路中点之间的连线,连接S和T形成一个集成的网络图。v1, v2, …, v27分别为每个自由链路的中心,表示机器人的可达点。
|
图 1 基于自由凸多边形的MAKLINK图 Fig. 1 MAKLINK diagram based on free convex polygon |
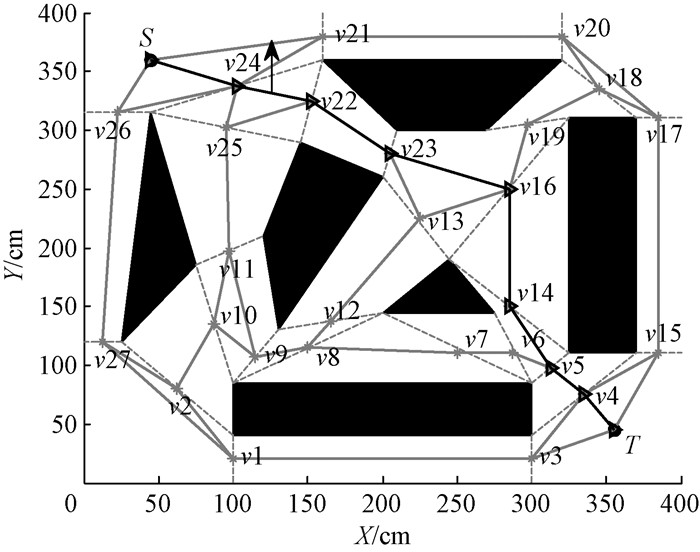
建立机器人的工作空间模型后,路径规划问题就转化为最短路径搜索问题。采用Dijkstra算法得到如图 2所示的由G=(ωi, j, V, E)表示的权重无向图的全局次优路径,其中:ωi, j是两个相邻中间点的距离;V是一系列的中点,表示图中所有顶点的集合;E是一组线,表示两个相邻自由链接的中点彼此连接的线。由Dijkstra算法得到的全局次优路径如图 2中实线所示,表示为S→v24→v22→v23→v16→v14→v5→v4→T。
|
图 2 Dijkstra算法得到的全局次优路径 Fig. 2 Global suboptimal path obtained by Dijkstra algorithm |
由于Dijkstra算法得到的机器人全局次优路径是沿着自由链路中心的连线行走,而不是在整个网络路径上行走。因此,该算法得到的并不是整个路径规划空间的最短路径。下一节将采用PSO算法对获得的次优路径进行二次优化,从而得到全局最优路径。
2 基于改进粒子群算法的最优路径规划 2.1 基本粒子群算法1995年Kennedy和Eberhart根据鸟群飞行觅食行为提出了BPSO算法。在BPSO算法中,粒子被初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过追随两个“极值”来更新自己,第一个极值是粒子本身所找到的最优解,称为个体极值pbest;另一个极值是整个种群找到的最优解,称为全局极值pgbest。所有粒子都有一个适应度值和速度,决定它们飞翔的方向和距离,然后粒子跟随当前的最优粒子在D维空间中搜索以寻求最佳方案[7]。BPSO算法描述为:假设在D维空间中,粒子总数为n,第i个粒子在D维搜索空间的位置表示为xi=[xi1, xi2, …, xiD],速度表示为vi=[vi1, vi2, …, viD],在D维搜索空间中,从t时刻到t+1时刻粒子的速度和位置更新公式可以分别表示为
| $ v_{id}(t+1)=\omega \times v_{id}(t)+c_{1} \times r a n d() \times\left[p_{ibest}(t)-x_{i d}(t)\right]+c_{2} \times r a n d() \times\left[p_{gbest}(t)-x_{id}(t)\right], $ | (1) |
| $ x_{i d}(t+1)=x_{i d}(t)+v_{i d}(t+1), $ | (2) |
式中:i=1, 2, …, n;d=1, 2, …, D;rand()为[0, 1]的随机数;ω为惯性系数;c1、c2为学习因子;vid表示D维空间中粒子的速度;xid表示D维空间中粒子的位置;pibest表示粒子本身所找到的最优解;pgbest表示整个种群中粒子所找到的最优解。
2.2 改进粒子群算法的路径规划由于BPSO算法在进行路径规划时选择最优的粒子进行学习,导致粒子数目急剧减少,造成了粒子的多样性降低,使粒子陷入局部最优。本文提出了SAPSO算法,即粒子更新速度时,粒子选择适应度值优于平均适应度值的粒子进行学习,并对低于平均适应度值的粒子进行变异处理。该方法增加了粒子的多样性,避免粒子陷入局部最优,使粒子快速收敛到全局最优。由图 1可知,路径与链接线的交点有7个,故搜索空间为7维,粒子的适应度函数可以表示为
| $ f(i)=\sum\limits_{i=1}^{8} \sqrt{\left(x_{i+1}-x_{i}\right)^{2}}, $ | (3) |
式中:i为维度序号。SAPSO算法的速度和位置更新公式可以分别表示为
| $ \bar{v}_{id}(t+1)=\omega \times \bar{v}_{id}(t)+\alpha_{1} \times r a n d() \times\left[\bar{p}_{gbest}(t)-\bar{x}_{id}(t)\right]+\alpha_{z} \times r a n d() \times\left[\bar{p}_{ad}(t)-\bar{x}_{id}(t)\right], $ | (4) |
| $ x_{i d}(t+1)=x_{i d}(t)+\bar{v}_{i d}(t+1), $ | (5) |
式中:ω为惯性权重系数;α1、α2为学习因子;i=1, 2, …, n;d=1, 2, …, D;rand()为[0, 1]的随机数;vid表示改进算法中粒子的速度;pgbest表示改进算法中种群粒子所找到的最优解;xid表示改进算法中粒子的位置;
| $ x_{w d}=x_{w d}+\left(\bar{x}_{i d}-x_{w d}\right) \times {rand}() \times\left(1-t / t_{\max}\right)^{\beta}, $ | (6) |
式中:xwd表示种群中适应度值低于平均适应度值的粒子的位置;tmax表示最大迭代步数;β表示非均匀变异的均匀度,一般取为2。早期提出的粒子群算法的速度项并没有系数,容易在前期陷入局部最优,产生早熟收敛。同时,由于迭代后的速度呈线性递增趋势,到后期无法进行较细的局部搜索,达不到完全避碰的路径规划要求。引入恒惯性权重系数[12]为ω=ωmax-t ·(ωmax-ωmin)/itermax, 其中:ωmax为初始权重;t为当前迭代次数;ωmin为最终权重;itermax为最大迭代次数。虽然改进权重系数的方法对求解最优化解问题有所改善,但效果并不明显。本文将指数变量权重引入改进粒子群算法中,将惯性权重系数修正为ω=ωmin(ωmax/ωmin)1/(1+10t/itermax)。考虑到粒子速度的大小会对路径的选择产生重要影响,如果粒子速度过大会掠过最优解,速度过小会陷入局部最优,所以将vmaxi取为位置变化范围的10%,并令
| $ v_{i d}^{t}=\left\{\begin{array}{ll} {v_{\max }, } & {v_{i d}^{t}>v_{\max }} ,\\ {-v_{\max }, } & {v_{i d}^{t}<-v_{\max }}, \end{array}\right. $ | (7) |
式中:vidt为粒子的速度; vmax为所允许的粒子的最大速度。
综上所述,采用SAPSO算法进行最优路径规划的步骤如下。
Step 1:初始化粒子种群大小n,惯性因子ω,加速因子c1、c2、α1、α2及迭代次数t。
Step 2:根据式(1)、式(2)初始化粒子的位置x和速度v。
Step 3:根据式(3)计算每个粒子的适应度值,并计算出粒子的平均适应度值。
Step 4:选出优于平均适应度值的粒子,并根据式(4)、式(5)更新适应度值优于平均适应度值的粒子的位置和速度。适应度值低于平均适应度值的粒子根据式(6)更新位置。
Step 5:若满足停止条件则停止搜索,并输出结果,否则返回Step 3。
3 仿真实验为验证本文所提出的SAPSO算法的有效性,在CPU为2.50 GHz、内存为4.00 GB的个人计算机上进行仿真验证。首先验证SAPSO算法的收敛性;其次在图 1所设置的障碍物环境中采用SAPSO算法进行仿真,并与其他改进PSO算法在适应度值、路径长度及运行时间方面进行对比;最后在不同障碍物环境中分别采用改进A*算法、改进RRT算法和SAPSO算法进行路径规划,并比较其性能。在仿真过程中SAPSO算法参数设置为:粒子总数n为100,迭代次数t为1 000。根据文献[13]提出的保证粒子群算法收敛的参数选择原则,将加速度系数设为c1=c2=1.4,ω=0.9,α1=α2=1.49。
为了降低算法随机性带来的影响,基于文献[9],采用单峰函数Rosenbrock和多峰函数Griewwank分别测试BPSO算法和SAPSO算法的收敛性。所采用的Rosenbrock函数和Griewwank函数可以分别表示为
| $ F(x)=\sum\limits_{i=1}^{D}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(x_{i}-1\right)^{2}\right], $ | (8) |
| $ F(x)=\frac{1}{4 \;000} \sum\limits_{i=1}^{D} x_{i}^{2}-\prod\limits_{i=1}^{D}\left(x_{i} / \sqrt{i}\right)+1。$ | (9) |
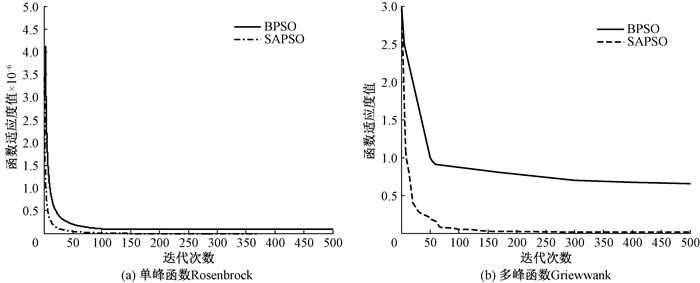
收敛性能对比结果如图 3所示。可以看出,在单峰函数Rosenbrock和多峰函数Griewwank下,SAPSO算法比BPSO算法具有更快的收敛速度。
|
图 3 收敛性能对比 Fig. 3 Convergence performance comparison |
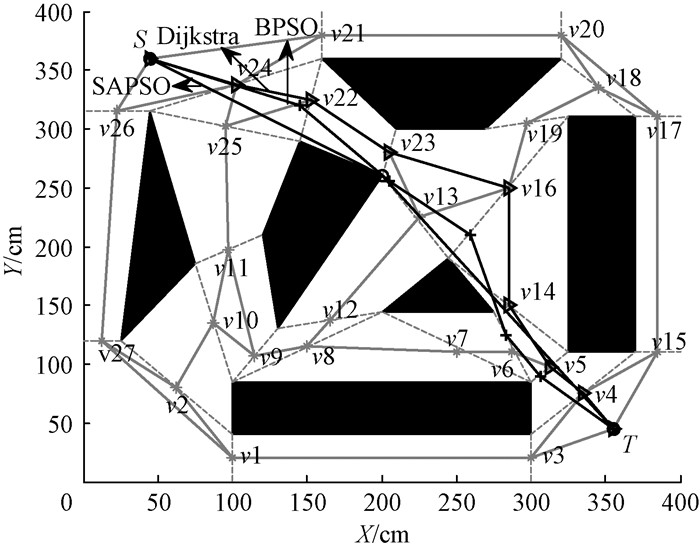
在图 1所设置的障碍物环境中采用SAPSO算法进行路径规划,并与Dijkstra算法和BPSO算法进行比较。图 4为基于3种算法得到的全局最优路径,其中黑色带三角路线为基于Dijkstra算法得到的路径,其长度为495.013 cm;黑色带加号路线为基于BPSO算法得到的路径,其长度为464.747 cm;黑色带圆圈路线为基于SAPSO算法得到的路径,其长度为449.506 cm。
|
图 4 基于3种算法得到的全局最优路径 Fig. 4 Global optimal path obtained by three algorithms |
此外,在图 1所设定的障碍物环境中,将SAPSO算法与BPSO、RCPSO[8]、JMPOPSO[9]、ACPSO[10]、DGPSO[11]等其他改进粒子群算法进行仿真比较[14],不同算法的路径规划性能对比结果如表 1所示。表 1记录了多种改进粒子群算法进行路径规划的适应度的最大值、平均值、最小值,以及路径长度和平均运行时间。由表 1可以看出,SAPSO算法的适应度值最大,规划的路径最短。由于SAPSO算法的时间复杂度只与粒子的维数有关[12],而其他改进算法的复杂度除了与粒子维数有关外,还与粒子数目、迭代次数有关,如DGPSO算法的时间复杂度为O(n*D*itermax)[11],当粒子数目较多时,复杂度将会增加。因此,SAPSO算法的复杂度相对较低,路径规划时间最短。
|
|
表 1 不同改进粒子群优化算法的路径规划性能对比 Tab. 1 Comparison of path planning performance among different improved particle swarm optimization algorithms |
移动机器人工作空间障碍物设置如图 5所示。在图 1、图 5所设置的障碍物环境中分别采用改进A*算法、改进RRT算法和SAPSO算法,在n=100、迭代次数为1 000的条件下进行路径规划,3种算法的路径规划性能对比结果如表 2所示。可以看出,SAPSO算法在3种障碍物环境中得到的路径均最短且规划成功率最高。改进A*算法由于计算量大而导致内存占用严重,且计算时间较长,并且改进A*算法中启发函数的选取非常重要,引入的启发信息过大或过小都会影响最优路径的搜索效率。改进RRT算法主要是在树的生长方式等方面进行了完善,提高了收敛速度,但是由于随机采样的性质,改进RRT算法前后两次得到的结果可能完全不同。相比于改进A*算法、改进RRT算法,本文所提出的SAPSO算法具有收敛速度快、参数少、实现简单等特点,且粒子在更新速度时不是向最优的粒子学习,而是向适应度值优于平均适应度值的粒子学习,并对低于平均适应度值的粒子进行变异处理,故该方法能够提高粒子的多样性,避免粒子陷入局部最优,实现了最短路径规划。
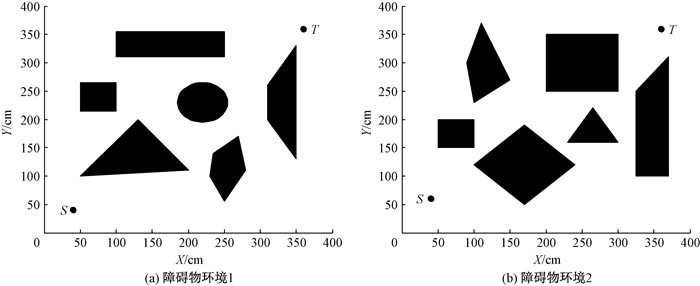
|
图 5 移动机器人工作空间障碍物设置 Fig. 5 Obstacle environments of the mobile robot workspace |
|
|
表 2 3种算法的路径规划性能对比 Tab. 2 Path planning performance comparison of three algorithms |
本文针对BPSO算法在路径规划时易陷入局部最优、规划路径较长等问题,提出了改进粒子群优化算法SAPSO,即当粒子更新速度时,粒子不是向最优的粒子学习,而是向适应度值优于平均适应度值的粒子学习,并对低于平均适应度值的粒子进行变异处理。将指数变量权重加入改进粒子群算法中,使粒子以最短的时间得到最优解。改进的粒子群算法提高了粒子的多样性,使粒子逃离局部最优。仿真结果表明,所提出的SAPSO算法具有适应度高、规划路径短、运行时间短等优点。
| [1] |
张捍东, 陈阳, 吴玉秀. 未知环境下移动机器人实时路径规划[J]. 计算机工程与应用, 2018, 54(19): 140-146. ZHANG H D, CHEN Y, WU Y X. Real time path planning for mobile robot in unknown environment[J]. Computer engineering and applications, 2018, 54(19): 140-146. DOI:10.3778/j.issn.1002-8331.1706-0225 (  0) 0) |
| [2] |
欧阳鑫玉, 杨曙光. 基于势场栅格法的移动机器人避障路径规划[J]. 控制工程, 2014, 21(1): 134-137. OUYANG X Y, YANG S G. Obstacle avoidance path planning of mobile robots based on potential grid method[J]. Control engineering, 2014, 21(1): 134-137. DOI:10.3969/j.issn.1671-7848.2014.01.031 (  0) 0) |
| [3] |
DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische mathematik, 1959, 1(1): 269-271. DOI:10.1007/BF01386390 (  0) 0) |
| [4] |
赵晓, 王铮, 黄程侃, 等. 基于改进A*算法的移动机器人路径规划[J]. 机器人, 2018, 40(6): 903-910. ZHAO X, WANG Z, HUANG C K, et al. Mobile robot path planning based on an improved A* algorithm[J]. Robot, 2018, 40(6): 903-910. (  0) 0) |
| [5] |
NOREEN I, KHAN A, RYU H, et al. Optimal path planning in cluttered environment using RRT*-AB[J]. Intelligent service robotics, 2018, 11(1): 41-52. (  0) 0) |
| [6] |
蒲兴成, 李俊杰, 吴慧超, 等. 基于改进粒子群算法的移动机器人多目标点路径规划[J]. 智能系统学报, 2017, 12(3): 301-309. PU X C, LI J J, WU H C, et al. Mobile robot multi-goal path planning using improved particle swarm optimization[J]. CAAI transactions on intelligent systems, 2017, 12(3): 301-309. (  0) 0) |
| [7] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN International Conference on Neural Networks. Perth, 1995: 1942-1948.
(  0) 0) |
| [8] |
SU K, WANG Y J, HU X N. Robot path planning based on random coding particle swarm optimization[J]. International journal of advanced computer science and applications, 2015, 6(4): 58-64. (  0) 0) |
| [9] |
李荣龙.基于改进粒子群优化算法的机器人路径规划研究[D].南京: 南京邮电大学, 2015. LI R L.Research on path planning of mobile robot based on improved particle swarm optimization algorithm[D].Nanjing: Nanjing University of Posts and Telecommunications, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10293-1015730756.htm (  0) 0) |
| [10] |
任子晖, 王坚. 加速收敛的粒子群优化算法[J]. 控制与决策, 2011, 26(2): 201-206. REN Z H, WANG J. Accelerate convergence particle swarm optimization algorithm[J]. Control and decision, 2011, 26(2): 201-206. (  0) 0) |
| [11] |
王燕燕, 葛洪伟, 王娟娟, 等. 一种动态分组的粒子群优化算法[J]. 计算机工程, 2015, 41(1): 180-185. WANG Y Y, GE H W, WANG J J, et al. A particle swarm optimization algorithm of dynamic grouping[J]. Computer engineering, 2015, 41(1): 180-185. DOI:10.3969/j.issn.1000-3428.2015.01.033 (  0) 0) |
| [12] |
杨景明, 穆晓伟, 车海军, 等. 多策略改进的多目标粒子群优化算法[J]. 控制与决策, 2017, 32(3): 435-442. YANG J M, MU X W, CHE H J, et al. Improved multi-objective particle swarm optimization algorithm based on multiple strategies[J]. Control and decision, 2017, 32(3): 435-442. (  0) 0) |
| [13] |
TANG B W, ZHU Z X, LUO J J. A convergence-guaranteed particle swarm optimization method for mobile robot global path planning[J]. Assembly automation, 2017, 37(1): 114-129. DOI:10.1108/AA-03-2016-024 (  0) 0) |
| [14] |
介婧, 徐新黎. 智能粒子群优化计算:控制方法、协同策略及优化应用[M]. 北京: 科学出版社, 2016. JIE J, XU X L. Intelligent particle swarm optimization: control method, cooperative strategy and optimization application[M]. Beijing: Science Press, 2016. (  0) 0) |
 2020, Vol. 52
2020, Vol. 52

