0 引言

高斯混合模型(Gaussian mixture model，GMM)的实质是通过多个高斯函数的加权平均和来刻画样本数据的分布。使用GMM进行聚类时，将数据视作若干高斯分布的加权组合，每个高斯分布均为一个类簇，选择所属概率最大的类簇作为对数据的划分结果。Huang等^[1]针对GMM需要事先确定聚类数目的问题，将探路者算法与高斯混合聚类相结合，根据数据集自动确定最优聚类数目。Wang等^[2]针对GMM聚类算法中需要更多的迭代次数和通信开销的问题，提出了基于迁移学习的分布式聚类GMM，利用迁移分布式GMM聚类框架提升聚类性能，加速聚类收敛。Zhang等^[3]针对GMM无法有效解决数据缺失的问题，提出由GMM聚类的结果填充缺失的数据，然后将插补数据用于GMM聚类。程宏兵等^[4]提出了基于GMM和自适应簇数的文本聚类算法，自适应文本聚类数量并获得其分布，实现海量文本的精确聚类。陈佳琪等^[5]从估计给定数据集的未知概率密度函数入手，建立了核密度估计与GMM之间的关联，提出了基于统计感知策略的GMM求解方法。

针对隶属关系不明确会导致GMM聚类存在较大的误判风险的问题，万仁霞等^[6]将三支决策思想融入GMM中，提出一种基于三支决策的高斯混合聚类模型(three-way Gaussian mixture model，T-GMM)，有效减小误判代价。然而，GMM和T-GMM在高维空间中进行聚类时，数据的稀疏性会干扰算法的聚类过程，从而影响聚类结果的准确性，降低算法的聚类质量。

属性约简是高维数据处理的一种重要手段，基于粗糙集理论的属性约简方法已经形成较为完备的理论体系^[7-10]。粗糙集理论(rough set，RS)^[11]是由波兰数学家Pawlak于1982年所提出的一种处理不确定性知识的数学工具。模糊粗糙集^[12]是粗糙集的一种模糊推广，依赖先验知识去设定隶属函数。邻域粗糙集(neighborhood rough set，NRS)^[13]则可以不依赖隶属函数和先验知识就能进行属性约简。在使用NRS进行属性约简时，当多个属性具有相同的重要程度时，Jia等^[14]通过比较属性的信息熵进行属性约简，并对约简后的数据集进行光谱聚类，使最终的聚类结果更接近真实类簇，从而获得更高的聚类精度。

虽然NRS相比其他粗糙集具有诸多优点，但其需要通过网格搜索的方式对半径参数寻优，造成大量的时间消耗。粒球邻域粗糙集(granular ball neighborhood rough set，GBNRS)^[15]不仅沿袭了NRS不依赖隶属函数和先验知识的优点，同时能够依据数据分布，自适应地生成合适的粒结构^[16]。为提高三支高斯混合聚类模型在高维空间的聚类质量，本文将GBNRS约简技术引入聚类过程，提出了基于GBNRS的三支高斯混合聚类。所提算法可有效消除冗余属性，提高三支高斯混合聚类在高维空间中的聚类质量，并且能够更准确地刻画类簇的边界信息。

1 相关理论 1.1 粒球邻域粗糙集

定义1 ^[17]   $U \subset \mathbf{R}^e $为数据集，$ U_0 \subseteq U$。GB为$ U_0\left(U_0 \neq \varnothing\right)$上生成的以Q为中心、r为半径的粒球，

$ \boldsymbol{Q}=\frac{1}{m} \sum\limits_{d=1}^m \boldsymbol{u}_d, $

(1)

$ r=\max \left\{dist\left(\boldsymbol{u}_d, \boldsymbol{Q}\right) \mid \boldsymbol{u}_d \in G B\right\}, $

(2)

$ H(G B)=\frac{\left|\left\{\boldsymbol{u}_d \in G B, Y\left(\boldsymbol{u}_d\right)=Y(G B)\right\}\right|}{|G B|}, $

(3)

其中：$ \boldsymbol{u}_d(d=1, 2, \cdots, m)$为粒球中的样本点；m为粒球中样本点的个数；$ dist\left(\boldsymbol{u}_d, \boldsymbol{Q}\right)$为$ \boldsymbol{u}_d$到Q的距离；Y(GB)为粒球整体的类标签，是GB中出现次数最多的类标签；H(GB)表示粒球的纯度，是GB中所有与粒球具有相同标签的样本的占比。

定义2 ^[15]   给定实数空间上的非空有限集合$ U=\left\{\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n\right\}$，在U上生成的粒球集定义为$ G B_s=\left\{G B_1, G B_2, \cdots, G B_s\right\}$。对于$ \boldsymbol{u}_i \in G B_t$定义$ \boldsymbol{u}_i(i=1, 2, \cdots, n)$的r-邻域为

$ r\left(\boldsymbol{u}_i\right)=\left\{\boldsymbol{u} \mid \forall \boldsymbol{u} \in G B_t, \left\|\boldsymbol{u}, \boldsymbol{Q}_t\right\| \leqslant r_t\right\}, $

其中：$ \boldsymbol{Q}_t, r_t$分别为第t个粒球的球心和半径，t=1, 2, …, s。

根据定义2可以看出，u_i的r-邻域就是与其同属一个粒球中的数据点所构成的集合。

定义3 ^[15]   给定邻域决策信息系统〈U, C, D〉，决策属性集D将U划分为N个等价类：X₁, X₂, …, X_N。C为条件属性集，对于$ \forall B \subseteq C$，决策属性集D相对于属性集B的生成下近似定义为

$ \underline{B } D^{\prime}=\bigcup\limits_{l=1}^N \underline{B } X_l^{\prime} \text { 。} $

式中，

$ \underline{B }X_l^{\prime}=\left\{\left.\boldsymbol{c}_t^{\prime}=\frac{1}{m_t} \sum\limits_{d=1}^{m_t} \boldsymbol{u}_d \right\rvert\, \boldsymbol{u}_d \in G B_t(B), r\left(\boldsymbol{u}_d\right) \subseteq X_l\right\}, $

其中：m_t表示第t个粒球中样本的数量。

D的生成正域定义为

$ \operatorname{GPOS}_B(D)=\underline{B }D^{\prime} \text { 。} $

定义4 ^[15]   给定邻域决策信息系统〈U, C, D〉，对于$ B \subseteq C$，若B是C的相对约简，则B满足：

$ \begin{gathered} \operatorname{GPOS}_B(D)=\operatorname{GPOS}_C(D), \\ \operatorname{GPOS}_B(D) \neq \operatorname{GPOS}_{B-\{b\}}(D), b \subseteq B_{\circ} \end{gathered} $

粗糙集通常在保持正域不变的条件下进行属性约简，与之同理，在定义4中GBNRS通过保持粒球的生成正域不变来进行约简。

1.2 三支聚类

Yu^[18]将三支决策思想引入数据的聚类分析中，提出了三支聚类的算法框架。对于每个类簇，三支聚类将论域U划分为核心域Co、边界域Fr和琐碎域Tr。核心域中的对象肯定属于该簇，边界域中的对象可能属于也可能不属于该簇，琐碎域中的对象肯定不属于该簇^[19]。三支聚类中的每个类通过核心域和边界域的二元组来表示，即Z={Co, Fr}。对于每个数据对象u_i，聚类决策规则为

$ \text { 若 } P\left(Z_j \mid \boldsymbol{u}_i\right) \geqslant \alpha \text {, 则 } \boldsymbol{u}_i \in C o(j) \text {; } $

$ \text { 若 } \beta <P\left(Z_j \mid \boldsymbol{u}_i\right)<\alpha \text { ，则 } \boldsymbol{u}_i \in \operatorname{Fr}(j) \text { 。} $

式中，

$ \left\{\begin{array}{l} \alpha=\frac{\lambda_{\mathrm{PN}}-\lambda_{\mathrm{BN}}}{\left(\lambda_{\mathrm{PN}}-\lambda_{\mathrm{BN}}\right)-\left(\lambda_{\mathrm{BP}}-\lambda_{\mathrm{PP}}\right)}, \\ \beta=\frac{\lambda_{\mathrm{PN}}-\lambda_{\mathrm{NN}}}{\left(\lambda_{\mathrm{BN}}-\lambda_{\mathrm{NN}}\right)-\left(\lambda_{\mathrm{NP}}-\lambda_{\mathrm{BP}}\right)}, \end{array}\right. $

(4)

其中：λ_PP、λ_BP、λ_NP分别表示当对象属于第j类时，将其划分到该类核心域、边界域和琐碎域的损失代价；λ_PN、λ_BN、λ_NN分别表示当对象不属于第j类时，将其划分到该类核心域、边界域和琐碎域的损失代价^[20]。

由决策规则可以得到三支聚类结果，

$ C S=\{(C o(1), F r(1)), \cdots, (C o(K), F r(K))\}, $

其中：K为类簇个数。

1.3 高斯混合聚类 ^[21]

高斯混合分布$P_M(\boldsymbol{u}) $由K个混合成分组合而成，每个混合成分对应一个高斯分布$P\left(\boldsymbol{u} \mid \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j\right) $，每个高斯分布均为一个类簇。p_j表示第j个高斯混合成分的先验概率，则$ P_M(\boldsymbol{u})$可表示为

$ P_M(\boldsymbol{u})=\sum\limits_{j=1}^K p_j \cdot P\left(\boldsymbol{u} \mid \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j\right), $

其中：$ \sum\limits_{j=1}^K p_j=1, p_j \geqslant 0 ; \boldsymbol{\mu}$为均值向量；Σ为协方差矩阵。

令随机变量z_i∈{1, 2, …, K}表示生成样本u_i的高斯混合成分，根据贝叶斯定理可以得出样本u_i由第j个高斯混合成分生成的后验概率，

$ \omega_i^j=P_M\left(z_i=j \mid \boldsymbol{u}_i\right)=p_j \cdot \frac{P\left(\boldsymbol{u}_i \mid \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j\right)}{\sum\limits_{h=1}^K p_h \cdot P\left(\boldsymbol{u}_i \mid \boldsymbol{\mu}_h, \boldsymbol{\Sigma}_h\right)}, $

(5)

$ L_i=\operatorname{argmax} \omega_i^j, $

(6)

其中：L_i为样本u_i的最大后验概率，其所属类簇即为对u_i的划分结果。当存在多个近似的后验概率时，GMM对样本做出误判的风险增大。

2 基于粒球邻域粗糙集的三支高斯混合聚类算法

相较于NRS使用固定的邻域半径，GBNRS通过适应不同粒球的尺寸来拟合数据分布，提供了更高的灵活性，并能实现更精确的聚类结果。本文提出了基于粒球邻域粗糙集的三支高斯混合聚类(three-way Gaussian mixture clustering model based on granular ball neighborhood rough set)，简称为GBT-GMM算法。该算法的主要目的是在高维空间进行高斯混合聚类时，为了降低数据稀疏性的影响，通过使用GBNRS对数据进行属性约简处理。

2.1 粒球集生成

粒球集生成在本文算法中具有重要意义，其主要思想为：对于数据对象集$ U=\left\{\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n\right\}$，将U视作初始大粒球，根据式(1)~(3)计算粒球的纯度H，若H低于纯度阈值θ，则使用k-means聚类算法将U分成k个新粒球；计算每个新粒球的纯度，若存在新粒球的纯度低于阈值θ，继续使用k-means聚类算法分割新粒球为k个更小的粒球，直至每个粒球的纯度不低于阈值θ。本文中k取值为2。

2.2 GBT-GMM算法

GBT-GMM算法具体步骤如下。

输入：样本集U，属性集A={a₁, a₂, …, a_e}，粒球纯度阈值θ，最大迭代次数I，收敛阈值ε，决策参数λ_PP、λ_NN、λ_NP、λ_PN、λ_BP、λ_BN。

输出：约简后属性集A，类簇划分结果。

Step 1   初始化A为A，高斯混合分布模型参数$ \Theta=\left\{\left(p_j, \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j\right) \mid j=1, 2, \cdots, K\right\}$。

Step 2  在U上生成粒球集，然后从粒球集中去掉只包含一个对象的粒球，以剩下的粒球数为聚类簇数，粒球的中心为初始质心，对剔除离群点的数据集进行k-means聚类，获得新粒球集。

Step 3  去掉纯度低于阈值θ的粒球，生成正域由纯度不低于θ的粒球的中心组成。

Step 4  如果从属性集A中去掉属性a_v后，以生成正域中的粒球中心为初始质心，再次使用k-means聚类获得新粒球集。若所有粒球的纯度都不低于阈值，表示生成正域不变，应删除属性$ a_v(v=1, 2, \cdots, e), \bar{A}=A-\left\{a_v\right\}$。从U中删除相应属性数据后，返回Step 2重新生成粒球集，并在经历Step 4时选择一个新属性。

Step 5  如果Step 4中存在纯度低于θ的粒球，则保留属性a_v。从A中选择一个新属性，回到Step 4，直至所有属性检查完毕，输出约简后的属性集。

Step 6  对约简后的数据集，根据(5)式计算u_i由各混合成分生成的后验概率ω_i^j，更新参数p′_j，μ′_j和Σ′_j。

Step 7  更新$ \Theta=\left\{\left(p_j, \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j\right) \mid j=1, 2, \cdots, K\right\}$为$ \Theta^{\prime}=\left\{\left(p_j^{\prime}, \boldsymbol{\mu}_j^{\prime}, \boldsymbol{\Sigma}_j^{\prime}\right) \mid j=1, 2, \cdots, K\right\}$，回到Step 6，当达到最大迭代次数I或者下限平均增益小于收敛阈值ε时停止更新，根据(5)式计算对象u_i属于各类簇的后验概率ω_i^j。

Step 8  根据(4)式计算决策阈值α和β，根据(6)式计算对象$ \boldsymbol{u}_i(i=1, 2, \cdots, n)$的最大后验概率L_i，L_i对应第j个高斯混合成分。若α≤L_i，将u_i划分到Co(j)；若β < L_i < α，将u_i划分到Fr(j)；若L_i≤β，将u_i划分到Tr(j)。

Step 9  输出划分结果，

$ C S=\{(C o(1), F r(1)), \cdots, (C o(K), F r(K))\} 。$

在Step 2中实现粒球集生成时，利用k-means算法对不满足纯度阈值要求的粒球进行分割，将每个类簇都视为一个子球。因为聚类后各类簇中的数据具有更高的相似性，所以相较于分割前，分割后的子球具有更高的纯度。对子球的纯度继续进行考察，若满足纯度要求，则停止分割，否则使用k-means算法继续分割，直至每个粒球的纯度都不低于纯度阈值。通过Step 4~Step 7对数据进行属性约简，并为聚类决策提供后验概率的计算依据，即在粒球集的基础上，对约简后的数据集计算对象由每个混合成分生成的后验概率。最后，将最大的后验概率与决策阈值α和β进行比较，从而将对象划分到类簇的核心域或边界域。在Step 6中，使用如下公式更新参数：

$ \begin{gathered} p_j^{\prime}=\frac{1}{n} \sum\limits_{i=1}^n \omega_i^j, \\ \boldsymbol{\mu}_j^{\prime}=\frac{\sum\limits_{i=1}^n \omega_i^j \boldsymbol{u}_i}{\sum\limits_{i=1}^n \omega_i^j}, \\ \boldsymbol{\Sigma}_j^{\prime}=\frac{\sum\limits_{i=1}^n \omega_i^j\left(\boldsymbol{u}_i-\boldsymbol{\mu}_j\right)\left(\boldsymbol{u}_i-\boldsymbol{\mu}_j\right)^{\mathrm{T}}}{\sum\limits_{i=1}^n \omega_i^j} 。\end{gathered} $

3 实验与结果分析 3.1 实验数据与实验环境

实验采用Python3.11.2语言编写，处理器为Intel(R) Core(TM) i7-9700(3.00 GHz)，存储器为16.0 GB，Windows 10操作系统，集成开发环境为PyCharm。实验使用的7个数据集均来自UCI数据库，相关信息见表 1。

3.2 实验结果分析

实验依据3种指标(准确率、戴维森堡丁指数和轮廓系数)对聚类效果进行评价。

1) 准确率(Acc)^[22]的计算公式为

$ A c c=\frac{n^{\mathrm{TT}}+n^{\mathrm{NN}}}{n^{\mathrm{TT}}+n^{\mathrm{TN}}+n^{\mathrm{NT}}+n^{\mathrm{NN}}}, $

其中：n^TT表示实际为正，被检测为正的样本数；n^NN表示实际为负，被检测为负的样本数；n^TN表示实际为正，被检测为负的样本数；n^NT表示实际为负，被检测为正的样本数。Acc值越高，聚类效果越好。

2) 戴维森堡丁指数(DBI)^[23]的计算公式为

$ D B I=\frac{1}{K} \sum\limits_{j=1}^K \max\limits_{j \neq q}\left(\frac{f_j+f_q}{\left\|o_j-o_q\right\|^2}\right), $

其中：f表示类中的所有样本数据到聚类中心o的平均距离；$ \left\|o_j-o_q\right\|^2$表示类j与类q之间的欧氏距离。DBI值越低，聚类效果越好。

3) 轮廓系数(SC)^[24]的计算公式为

$ \begin{gathered} S C=\frac{1}{n} \sum\limits_{i=1}^n S_i, \\ S_i=\frac{w_i-g_i}{\max \left(g_i, w_i\right)}, w_i=\min \left\{M\left(\boldsymbol{u}_i-Z_j\right)\right\}, \end{gathered} $

其中：S_i为单个样本u_i的轮廓系数；g_i为样本u_i到所属簇中其他样本的平均距离；$ M\left(\boldsymbol{u}_i-Z_j\right)$表示样本u_i到类簇Z_j中所有样本的平均距离；w_i为样本u_i到距离最近的其他簇中所有样本的平均距离。SC值越大，聚类效果越好。

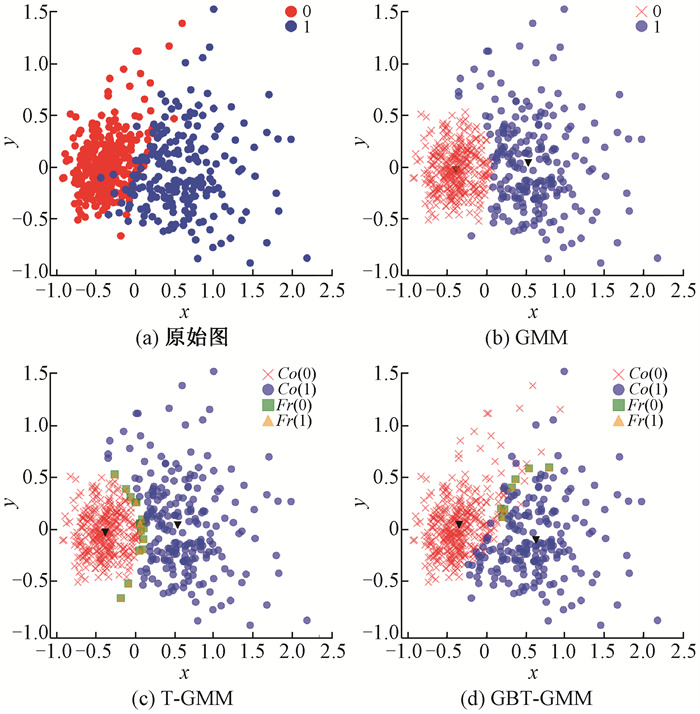
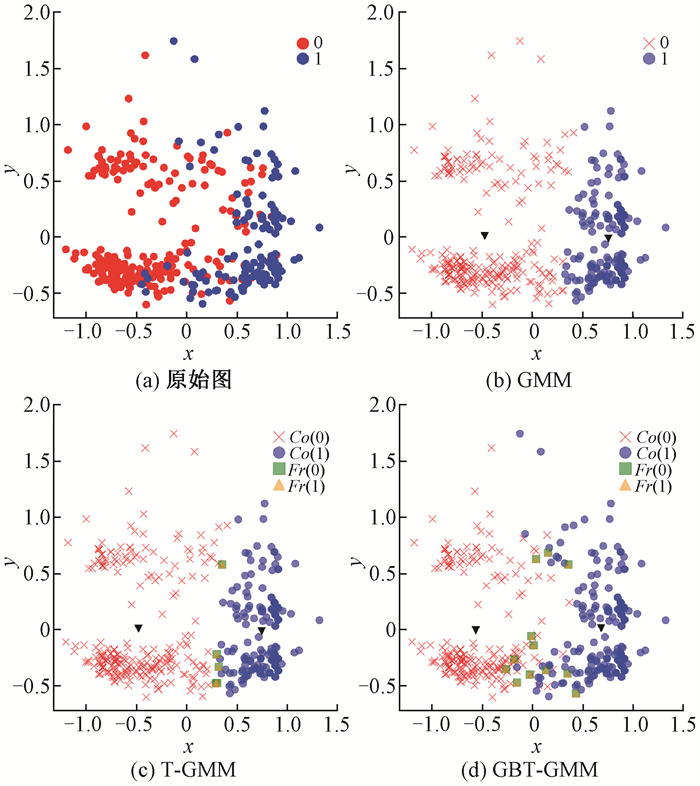
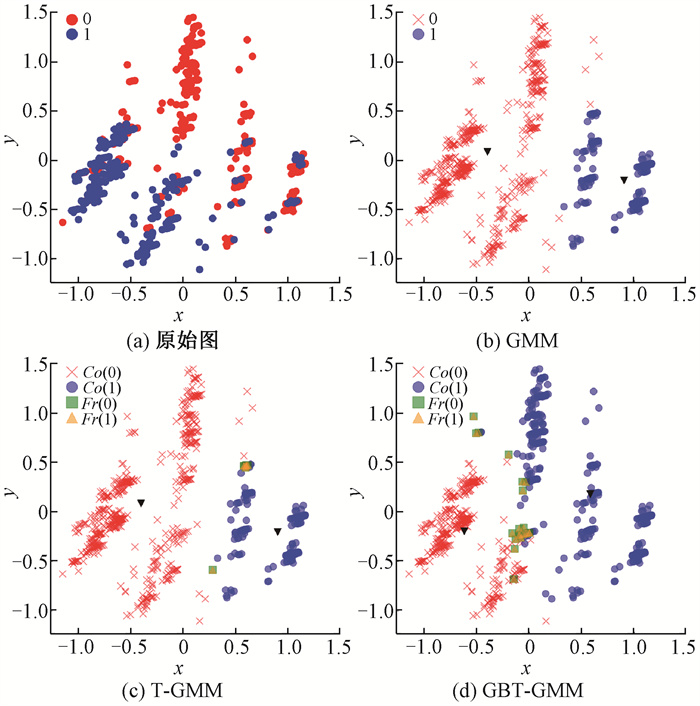
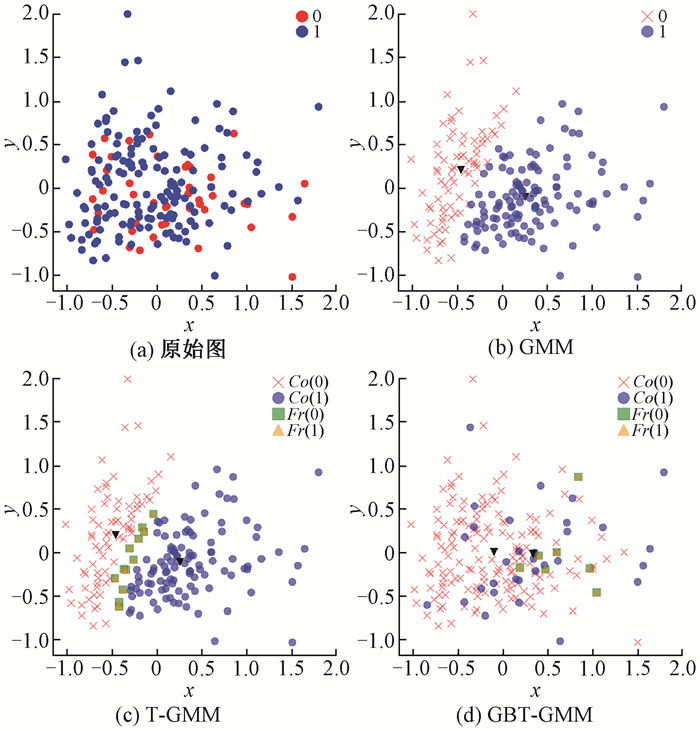
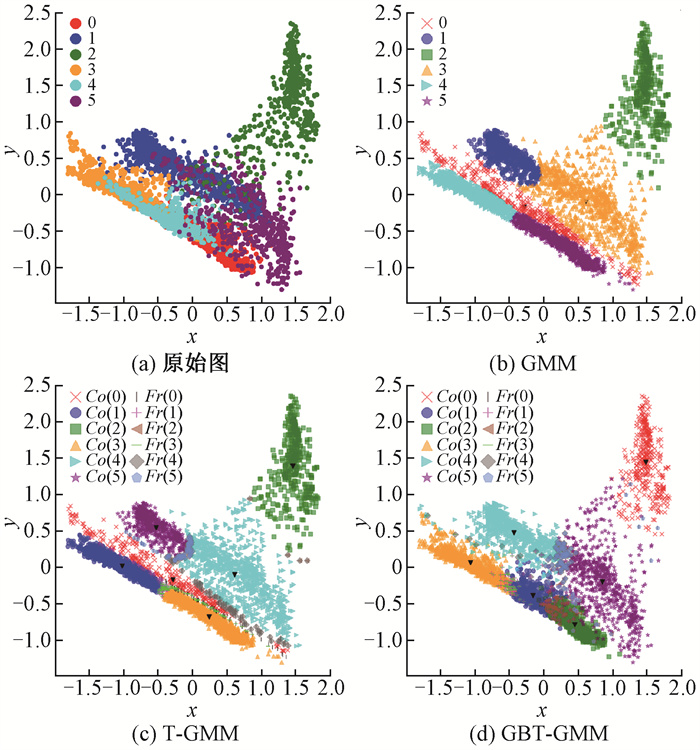
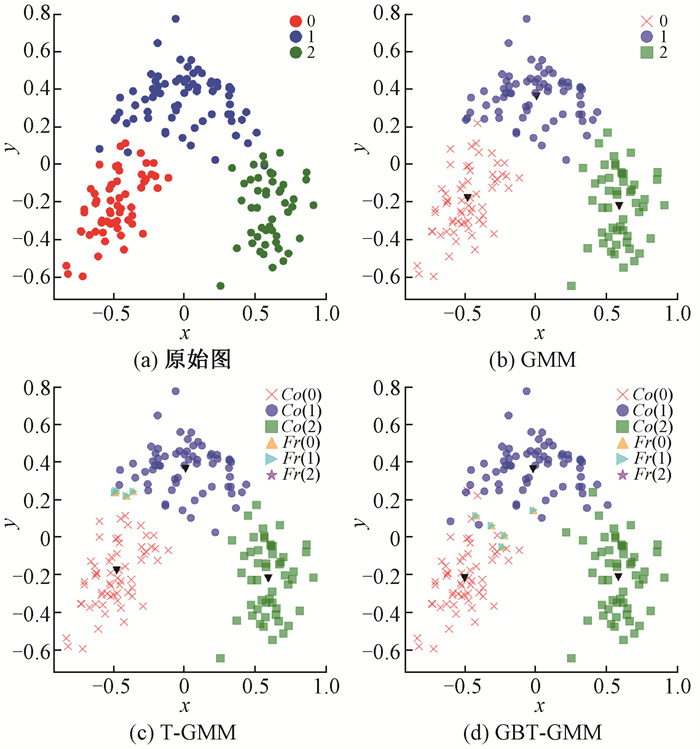
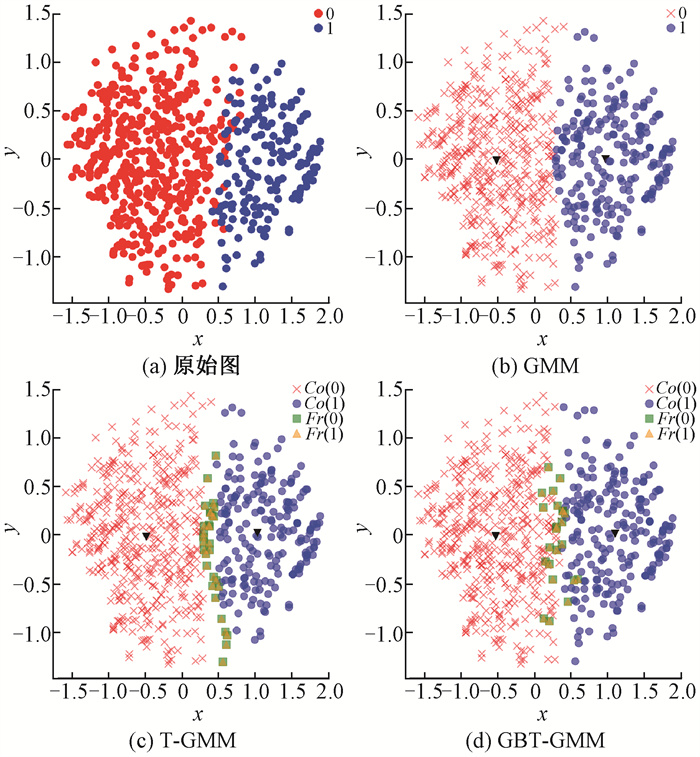
在实验过程中设定λ_PP=0，λ_NN=0，λ_NP=18，λ_PN=8，λ_BP=9，λ_BN=4，根据式(4)计算得到阈值参数为α=0.615，β=0.308。最大迭代次数I设定为100，收敛阈值ε设定为0.001^[6]，纯度阈值设定为1。图 1~图 7分别给出了7个数据集上GMM^[21]、T-GMM^[6]与GBT-GMM算法的聚类结果，图中x，y为二维笛卡尔坐标系的坐标轴，Co(i)为类簇i的核心域，Fr(i)为类簇i的边界域，黑色倒三角为类簇中心。

从图 1~图 7可以直观地看出，GBT-GMM在高维空间中对类簇的划分更加接近原始数据的真实分布。为了进一步验证GBT-GMM的聚类质量，对GBT-GMM、T-GMM和GMM在选定的评价指标下进行实验对比，结果见表 2。可以看出，GBT-GMM在这7个数据集上相比其他算法具有更高的SC值和更低的DBI值。同时，除了wine和autism两个数据集，GBT-GMM在其他5个数据集上还具有更高的Acc值。表明在这些数据集上，GBT-GMM的聚类效果总体上优于两种对比算法。在autism数据集上，虽然GBT-GMM的Acc指标略逊于T-GMM，但差值非常小，通常属于正常的误差波动，对聚类效果的影响有限，但GBT-GMM在SC和DBI值上优势明显。对于wine数据集，GBT-GMM在Acc值上略低于对比算法，由图 6可见，类簇之间重叠部分较小，分布较为均匀，很难进一步提升准确率。

GBT-GMM具有良好的聚类性能，其属性约简策略起到了重要作用。表 3中展示了GBT-GMM对7个实验数据集的属性约简结果。可以看出，约简后7个数据集的属性数均显著减少，达到了去除不相关或冗余属性的目的，减少了计算处理的消耗。属性约简后，避免了过多无关信息的干扰，模型聚类效果得到提升，进一步验证了属性约简的有效性。

GMM和T-GMM算法的时间复杂度均为O(neK)，其中n为样本点的数量，e为数据维度，K为混合成分的数量。使用GBNRS约简的时间复杂度为O(n)^[15]，设约简后数据维度为e′，则GBT-GMM算法的总体时间复杂度为O(ne′K)。由于e′ < e，因而GBT-GMM比GMM和T-GMM具有更小的时间复杂度。

综上所述，本文提出的GBT-GMM在实验数据集上具有较好的聚类效果，达到了其对高维空间数据属性约简的目的。

4 结语

本文在三支高斯混合聚类的基础上，结合GBNRS理论来提升算法在高维空间的聚类质量。所提出的GBT-GMM继承了T-GMM优越的聚类性能，实现了对高维数据的属性约简效果。实验结果表明，本文算法相较于对比算法，整体上具有更高的Acc和SC值以及更低的DBI值，能够有效消除冗余属性对高维聚类的负面影响，保留数据集的关键信息，使类簇之间更加紧凑，对类簇边界部分的刻画也更加准确。由于GMM使用EM算法来估计参数，在未来的工作中，将针对EM算法本身存在的缺陷进行优化，以进一步提高GBT-GMM的聚类效果，并在相关领域进行应用研究。