2. 四川港投川南临港产业投资(集团)有限公司 四川 成都 644004
2. Sichuan Port Investment Southern Sichuan Port Industry Investment (Group) Co., Ltd., Chengdu 644004, China
我国城市化进程的加快带来了交通拥堵等问题,准确的交通流预测可以为城市的交通管控与车辆调度提供有价值的建议,减少交通事故发生[1]。目前交通流预测方法可以大致分为统计学方法、机器学习方法和深度学习方法。
统计学方法通过大量数据来搭建时间序列数学模型,例如历史平均法(HA)、自回归积分移动平均模型(ARIMA)等。研究者们根据ARIMA模型又进行了改进,Van Der Voort等[2]提出了KARIMA模型,提升了预测的准确性与健壮性。杨高飞等[3]结合ARMA模型和卡尔曼滤波模型来预测交通流量,解决了ARMA模型在复杂道路情况下预测精度不高的问题。Williams等[4]使用SARIMA模型进行了交通流量预测,实验结果表明,相较于其他时间序列模型,SARIMA模型的预测结果更为稳定。
机器学习预测方法可以对历史交通流数据进行特征提取。SVR、SVM借助支持向量与核函数对交通数据分别处理,在小样本和高维度上取得了不错的效果[5-6]。杨兆升等[7]提出了一种基于SVM的短时交通流预测。SVM和SVR通过将非线性数据映射到高维空间来实现预测。Lippi等[8]提出了两个基于季节性核的支持向量回归模型,提高了交通流预测的准确性,但是需要消耗较高的计算资源。
深度学习以其优秀的性能而被广泛应用[9]。Zhao等[10]提出T-GCN用于短时交通预测,这是一种将GCN和GRU相结合的模型。Graph WaveNet[11]是一种基于图卷积和空洞卷积相结合的模型,采用节点嵌入的方式,学习自适应依赖性矩阵,从而精确地捕获数据中隐藏的空间依赖关系。Pan等[12]考虑了节点和道路的元信息,学习交通流预测中的时空相关。Guo等[13]将切比雪夫图卷积和一维卷积结合起来进行交通流量预测,设计了注意力模块,能够动态地调节时空序列在时间和空间维度上的相关性强度。Bai等[14]提出了时间卷积网络(TCN),TCN通过多层堆叠和膨胀卷积来扩大它的感受域,以此来捕获序列之间的长期相关性,然而多层的TCN堆叠会导致模型学习能力下降[15]。Zheng等[16]提出一种图多注意力模型,集合了空间注意力、时间注意力和变换注意力。STSGCN[17]是一种时空同步图卷积网络模型,它构造多个局部时空图来同步捕获时空依赖关系,但是它学习的参数是静态的,无法建模交通流数据的动态性与异质性。
目前工作都集中在提升准确度上,鲜有研究从交通序列中去分析交通流数据产生的根本来源,因此本文从数据的角度出发,提出了一种基于变分自编码器的交通流预测模型(AST-VAE)。本文的主要贡献包括以下3个方面。
1) 提出一种基于变分自编码器的交通流序列分离模型,通过变分推断和残差降解来分离交通流信号中隐藏的扩散信号、固有信号和随机信号,对不同来源的隐藏信号分别进行有效建模。
2) 基于分离模型设计三种不同信号学习模块捕获不同信号的时间相关性和空间相关性。
3) 基于两个真实的交通数据集对模型进行有效性与可行性分析,结果表明AST-VAE始终优于现有模型。
1 问题定义本文基于给定的路网传感器拓扑结构G和历史交通流特征矩阵X,使用模型f(·)预测未来J时间步的交通流量信息,表示为
AST-VAE的模型框架如图 1所示,模型由多个时空分离学习层和全局时空依赖模块组成,时空分离学习层包括分离模块和三个学习模块。
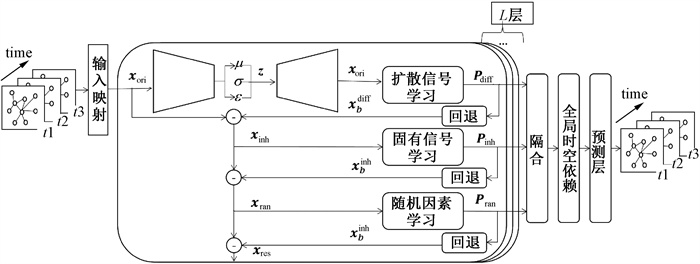
|
图 1 AST-VAE模型框架 Fig. 1 The structure of AST-VAE |
变分自编码器通过概率编码器和序列生成器学习所有传感器在每个时间步t的观测值xt的扩散信号参数化分布。编码器处理输入的信息序列推断后验分布Pθ(z | x),生成器通过门控采样机制和LSTM解码编码状态,汇总输入的信息序列,生成交通信号扩散部分的概率分布。
变分自编码器的生成目标是在生成模型
本节采用LSTM对交通流信号进行编码,获取传感器节点的上下文信息。解码器模型Pθ(x′t | zt)建模概率分布P(x′t | zt)即解码隐变量输出重构数据分布,数据的条件分布生成过程为Pθ(z)Pθ(x′t | zt)为了方便计算,将目标优化函数转化为最大化证据下界ELBO(evidence lower bound),计算公式为
| $ \begin{aligned} & \operatorname{loss}(\theta, \varphi)=-E_{z \sim q_{\phi(z \mid x)}} \log p_\theta\left(\boldsymbol{x}^{\prime} \mid \boldsymbol{z}\right)+ \\ & D_{K L}\left(q_{\varphi}(\boldsymbol{z} \mid \boldsymbol{x}) \| P(\boldsymbol{z})\right) \text { 。} \end{aligned} $ |
其中:‖表示向量拼接。
2.1.2 门控采样机制现实世界的交通数据具有全局周期性和局部周期性,因此本文设计了基于时间的周周期性张量和日周期性张量,引入两个时间嵌入矩阵AD∈ RN×C×d,AW∈ RN×C×d,其中:AD中的N为一天中传感器的采样频次;C为特征维度,表示当前的门值需要过去d天相同时间段的t个交通图信号;AW中N表示一周的7天;C为特征维度,表示当前门值需要前d周内有相同星期属性的t个交通图序列数据。在时间位置编码时,引入一个时间位置嵌入矩阵T ∈ RM×Q×D,M表示路网节点个数,Q和D表示节点在时间上的相对位置。在空间位置编码时,设计一个节点嵌入矩阵E ∈ RN×C,表示每一个节点空间位置设置一个向量表示,其中N为节点个数,C为特征维度。T和E为输入前预先定义好的时间位置信息与空间位置信息,输入模型后将表示时间周期性的矩阵AD和AW作为参考,将这些特征拼接在一起通过两个全连接层产生对应的阈值,采样机制可以表示为
| $ \begin{gathered} \boldsymbol{\varepsilon}=\operatorname{sigmoid}\left(\operatorname{ReLU}\left(\left(\boldsymbol{A}^D\left\|\boldsymbol{A}^W\right\| \boldsymbol{T} \| \boldsymbol{E}\right) \boldsymbol{W}_1\right) \boldsymbol{W}_2\right), \\ \boldsymbol{X}_{\text {out }}=\boldsymbol{\varepsilon} \odot \boldsymbol{z}, \end{gathered} $ |
其中:W1、W2是可学习参数;‖表示向量拼接;sigmoid、ReLU为非线性激活函数;⊙为向隐向量空间中的隐变量逐元素乘积。
2.2 残差降解机制本文设计了残差降解机制,以信息重构方式去除已经分离出来的交通流信号。通过分离时空层中每个模块的回退分支重新构造学习知识,回退分支的信号输出返回到原始输入信号中,通过一个残差连接将估计后的信号从原始信号中删除,保留还未充分分解的信号,实现信号的逐步分解。在第一个交通扩散信号的分离后,经过残差降解,得到了交通固有信号的输入,
| $ \boldsymbol{X}^{\text {inh }}=\boldsymbol{X}^{\text {ori }}-\boldsymbol{X}_b^{\text {diff }}=\boldsymbol{X}^{\text {ori }}-\sigma\left(\boldsymbol{P}^{\text {diff }} \boldsymbol{W}\right), $ |
其中: Xori是原始信号的输入; Xinh表示固有信号; Xdiff b表示分支回退的未充分分解的信号, 代表输出的交通流扩散信号; W为可学习参数, 采用非线性的多层感知机制去除第一次已分离出来的扩散信号。同理, 按照此方法, 利用回退分支的残差连接, 可以继续分离信号中的交通流固有序列, 得到信号中的随机和不确定序列, 分别计算为
| $ \begin{aligned} & \boldsymbol{X}^{\mathrm{ran}}=\boldsymbol{X}^{\mathrm{inh}}-\boldsymbol{X}_b^{\mathrm{inh}}=\boldsymbol{X}^{\mathrm{inh}}-\sigma\left(\boldsymbol{P}^{\mathrm{inh}} \boldsymbol{W}\right), \\ & \boldsymbol{X}^{\mathrm{res}}=\boldsymbol{X}^{\mathrm{ran}}-\boldsymbol{X}_b^{\mathrm{ran}}=\boldsymbol{X}^{\mathrm{ran}}-\sigma\left(\boldsymbol{P}^{\mathrm{ran}} \boldsymbol{W}\right), \end{aligned} $ |
其中:Xran为交通流的随机序列,最后随机序列残差降解后剩余的序列为Xres,则会进入下一个时空分离层。
2.3 局部时空依赖模块本节设计了一种并行的局部时空学习模块,由空间注意力模块和时间注意力模块构成。
2.3.1 空间注意力模块任意时刻自适应子图学习模块可以在不同时刻根据道路交通信息生成不同的邻接子图,从而刻画t时刻节点的时空关联关系的动态强度。
本文将自适应学习机制与图注意力网络(GAT)相结合构成空间注意力模块AGAT,用于提取交通道路的空间相关性。GAT的输入为节点特征矩阵Xt与自适应邻接矩阵At,在t时间步长内观察到的交通流属性为
本文使用带有注意力机制的LSTM网络来学习局部时空的依赖性,具体来说,任意时刻t的LSTM层输出数据都将被送入时间注意力部分得到输出值。
对于交通流固有信号和随机信号,采用带注意力机制的LSTM进行时间相关性捕获,经过多层时间捕获模块堆叠,数据输出为Xt∈ Rn×F″×T。对于交通流扩散信号,采用带注意力机制的自适应图卷积层代替LSTM中的三个门控的线性操作,即分别控制信息的输入、输出和遗忘,结构见图 2。
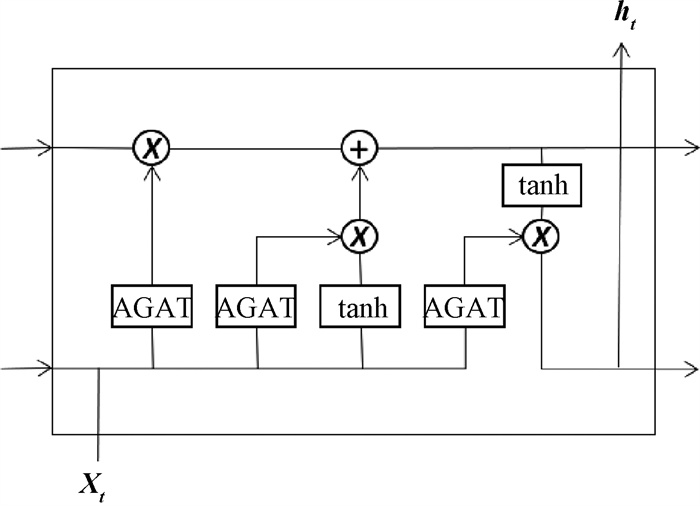
|
图 2 AGAT嵌入LSTM Fig. 2 AGAT embedding into LSTM |
全局时空依赖模块并行处理输出序列,通过时间卷积形式和残差连接,获取了比LSTM更强大的长期时间相关性,结构如图 3所示。在此之前,融合层将不同类别的时空特征进行一次融合操作,计算为
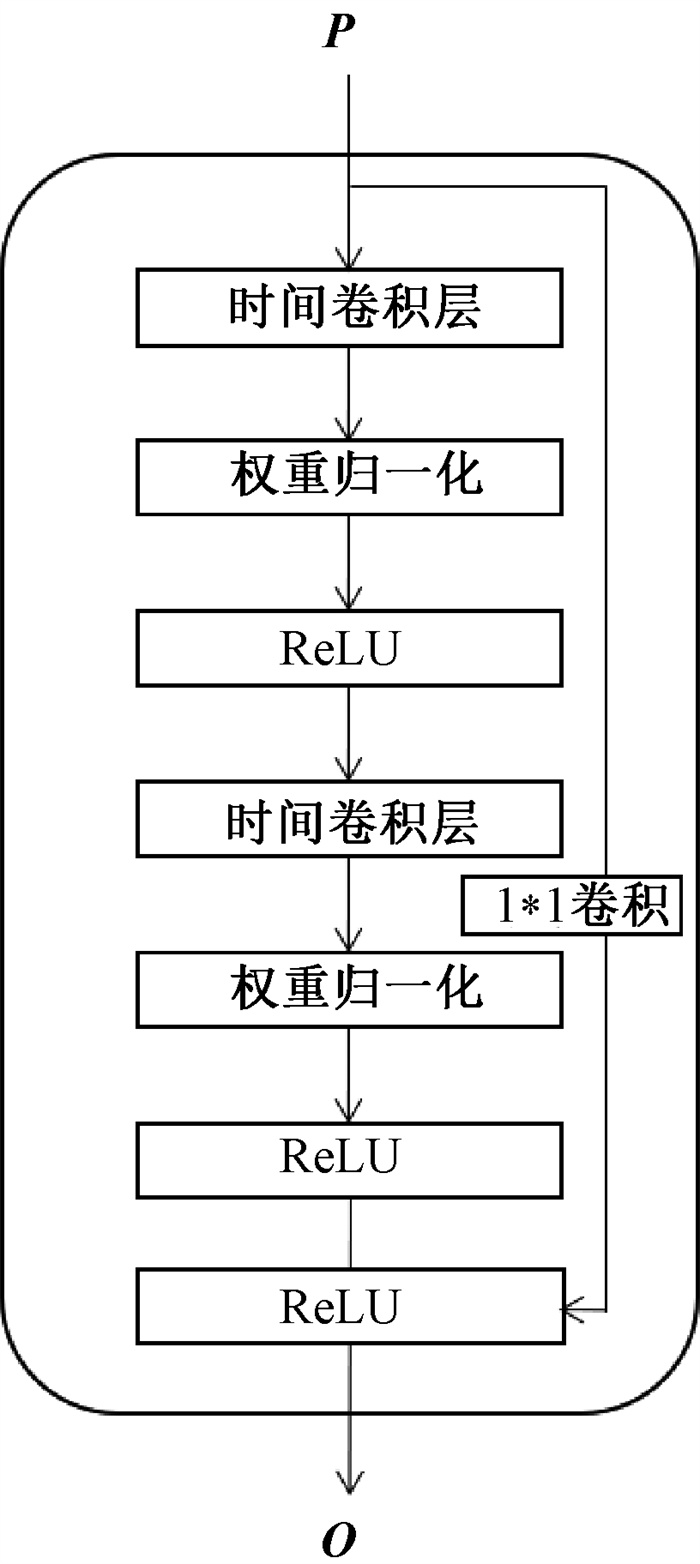
|
图 3 全局时间依赖 Fig. 3 Global temporal dependency |
| $ \boldsymbol{P}=\sum\limits_{i=1}^L\left(\boldsymbol{P}_i^{\mathrm{diff}}+\boldsymbol{P}_i^{\mathrm{inh}}+\boldsymbol{P}_i^{\mathrm{ran}}\right), $ |
时间序列卷积的计算为
| $ F(s)=\left(\boldsymbol{M} * \boldsymbol{d}^f\right)(s)=\sum\limits_{i=0}^{k-1} f(i) \cdot \boldsymbol{H}_{s-d \cdot i}, $ |
其中:d为空洞系数;k为卷积核大小;s-d ·i代表时间过去的方向,d=0时,卷积为普通一维卷积,最后经过残差连接输出,
| $ \boldsymbol{O}=\operatorname{Activation}(\boldsymbol{x}+F(\boldsymbol{x})) \text { 。} $ |
本实验基于Pytorch实现,处理器为Intel(R) Core(TM) i7-10700。在模型的超参数设计中,模型通过Adam进行优化,迭代轮次为300,批量大小为64,学习率设置为0.001,分离时空层层数为3,节点和时间的嵌入维度C为12,特征通道的数量d为32,卷积核大小k为2,GAT的注意力头数h为8,时间注意力层的头数h为6。
3.2 数据集介绍本文采用PEMSD4数据集和PEMSD8数据集来进行交通流预测模型的实验验证,两个数据集所有数据均由Caltrans性能测量系统(PeMS)收集得到的美国加利福尼亚州的高速公路交通数据集,数据集内容见表 1。
|
|
表 1 数据集描述 Tab. 1 Dataset description |
本文使用平均绝对误差(MAE),均方根误差(RMSE) 和平均绝对百分比误差(MAPE)对模型进行评估,3个指标的值越低,模型的预测精度越高。每个实验进行5次,然后计算平均值作为测试结果。
3.4 基准模型预测性能比较本节将模型AST-VAE与近期效果较好的6个交通流量预测模型进行比较。
1) Graph WaveNet:结合GCN提出一种自适应邻接矩阵学习节点的动态相关性。
2) STSGCN:时空同步图卷积网络模型,它构造多个局部时空图来同步捕获时空依赖关系。
3) DCRNN[18]:扩散卷积递归神经网络模型,使用扩散卷积替代GRU中的完全连接层,形成新的扩散卷积门控递归单元。
4) STGCN[19]:时空图卷积网络结合谱域上的GCN和一维卷积来捕获时间和空间相关性。
5) ASTGNN[20]:基于注意力的时空图神经网络模型,是一种将时间趋势自注意力机制与动态图卷积相结合的自注意力交通预测模型。
6) STG-NCDE[21]:该模型设计了两个独立的神经控制微分方程来建模空间和时间相关性。
表 2显示了AST-VAE在未来一小时(12个时间步)两个高速公路数据集上的预测结果,并进行t检验,结果具有统计学意义(p<0.005)。根据实验结果显示,AST-VAE在两个数据集的表现始终优于其他所有模型,均取得了最小的误差,证明了本文所提出的方法在交通流预测方面的有效性。同时可以发现随着预测时间步的增加,所有模型的性能将会变得更差,这是由于未来不确定性和极端情况的出现影响了模型,图 4展示了各模型随时间变化的结果。
|
|
表 2 各个模型在两个高速公路数据集的预测结果 Tab. 2 Prediction results of each model on two highway datasets |
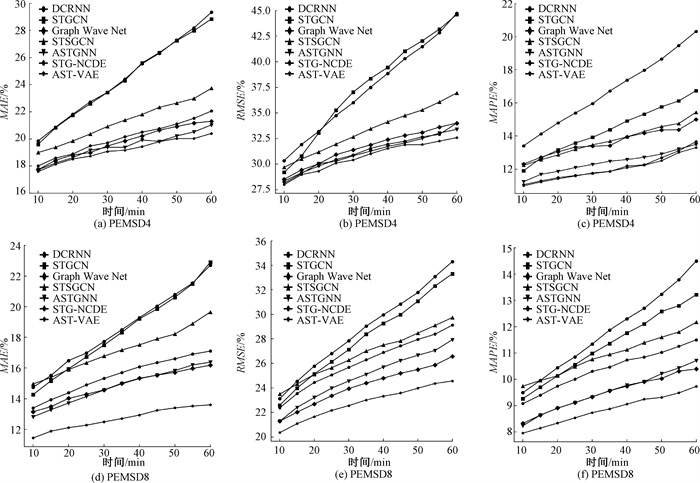
|
图 4 AST-VAE与基准模型在两个高速公路数据集上预测结果随时间变化情况 Fig. 4 The prediction results of AST-VAE and baseline models on two highway datasets over time |
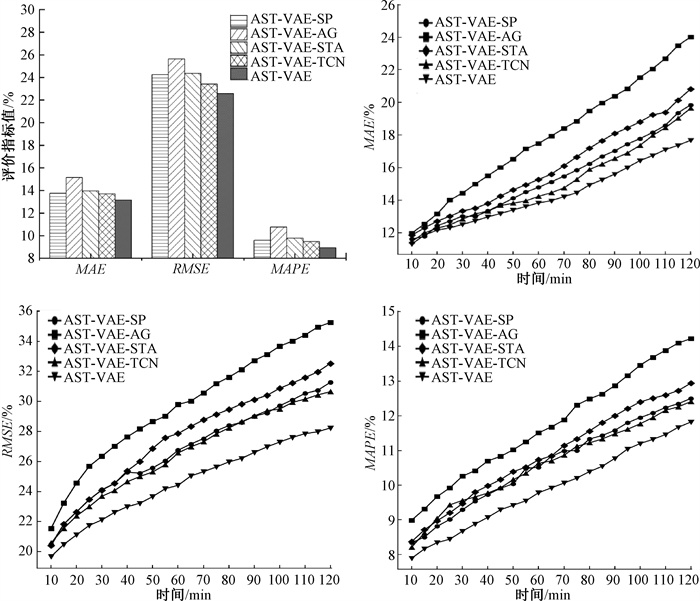
为了研究不同模块在AST-VAE模型中的有效性,对AST-VAE及其变体在PEMSD8上进行了消融实验,设计了以下几个变体。
1) AST-VAE-SP: 去除模型的变分自编码器,不考虑交通序列中的隐藏序列。
2) AST-VAE-AG: 去除模型中的自适应子图学习,采用静态拓扑建模空间相关性。
3) AST-VAE-STA: 去除模型中的时间注意力和空间注意力。
4) AST-VAE-TCN: 去除模型中的全局时空依赖模块,将各序列直接经过预测层输出。
除了上述差异外,所有变体模型的设置都与AST-VAE相同,图 5展示了不同变体之间的比较结果。比较AST-VAE-SP与AST-VAE实验结果可以看到模型对于序列的推断生成是非常重要的,对于交通序列中的不同成分分别建模有效提升了模型预测的准确性,解决了图卷积不能应用于传感器固有序列与随机序列的问题。AST-VAE-AG在采用预定义图情况下,效果要比AST-VAE差很多,这证明了空间相关性的学习是一个强动态连接的过程,通过自适应子图的学习对于流量预测的性能增益有积极的贡献。
|
图 5 PEMSD8数据集消融分析实验结果 Fig. 5 Results of ablation analysis experiments on PEMSD8 dataset |
AST-VAE-STA证明了空间学习模块和时间学习模块的多头注意力是另一个可以提高预测性能的重要因素,动态调整空间传感器之间以及时间步之间的相关强度是非常重要的。最后发现AST-VAE-STA在长期预测方面落后于AST-VAE-TCN,这证明了注意力机制优于时间卷积,AST-VAE优于AST-VAE-TCN,并且性能的差异随着时间的增大而变大,这证明了本文的全局时空依赖模块有效捕捉了数据的长期依赖性。
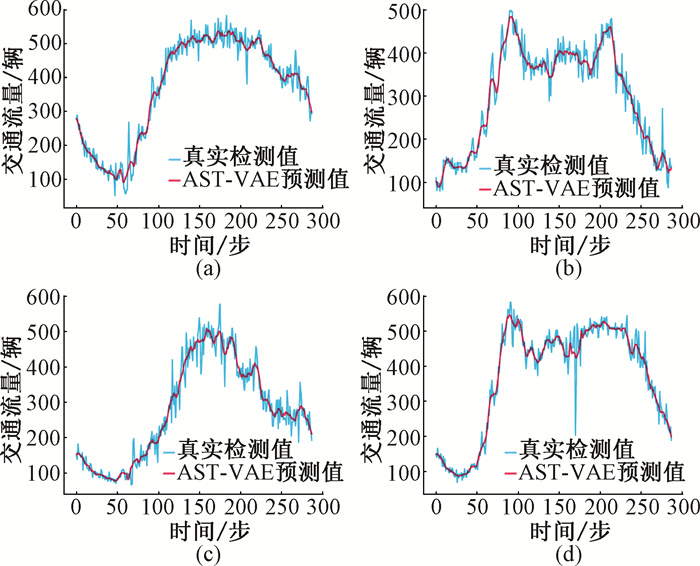
3.6 实验结果可视化在两个数据集中分别选择同一时间两个不同位置的探测器节点,图 6(a)、(c)是商业区,图 6(b)、(d)是居住区,并绘制真实监测值与AST-VAE的预测值对比图,如图 6所示。
|
图 6 PEMSD4和PEMSD8数据集真实值与预测值对比 Fig. 6 Comparison of actual values and predicted values on PEMSD4 and PEMSD8 dataset |
AST-VAE考虑了传感器节点固有的交通序列和不确定的随机序列,对时空数据的时间随机性与空间异质性进行了建模,可以捕获不同空间位置所具有的特定模式,图 6(a)节点与(b)学习的固有模式不同,(a)中节点由于处于商业聚集地,会在中午达到高峰,而(b)中节点由于居住区上下班的关系,会在早晚达到高峰。同时AST-VAE避免了过拟合,当道路交通出现突发事件时,本文的模型不会刻意拟合这些噪声,而是根据交通流中各种隐藏的信号充分利用模型中所学习的潜在交通相互作用,快速纠正极端情况下的探测值并正确预测。如图 6(d)第160个时间步左右,当出现了传感器损坏导致探测结果与当时交通状况不符的特殊情况,本文的模型做出了正确的流量预测。
4 结语本文考虑了交通流信号隐藏的时空相关性与随机性,提出了一种基于变分自编码器的交通流预测模型。该模型通过变分自编码器将交通流信号分解为隐藏的扩散信号、固有信号以及随机信号,随后对不同的信号进行混合建模,解决了隐藏序列建模不可靠的问题。通过多个时间步的自适应子图结合空间注意力捕获扩散信号的空间相关性,门控图卷积的长短型记忆网络则学习扩散信号的时间相关性。接着时间注意力模块提取固有信号以及随机信号的时间特征。最后使用全局时空依赖模块,增强了模型长期预测的能力。本文对AST-VAE模型的核心框架设计原理进行了详细分析和论述,并在公开的数据集上进行模型评估和对比实验,结果显示本文的模型优于现有模型,可以更好地探索交通流数据中的时空依赖性和非线性关系。
| [1] |
DIAO Z L, WANG X, ZHANG D F, et al. Dynamic spatial-temporal graph convolutional neural networks for traffic forecasting[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2019: 890-897.
(  0) 0) |
| [2] |
VAN DER VOORT M, DOUGHERTY M, WATSON S. Combining Kohonen maps with ARIMA time series models to forecast traffic flow[J]. Transportation research part C: emerging technologies, 1996, 4(5): 307-318. (  0) 0) |
| [3] |
杨高飞, 徐睿, 秦鸣, 等. 基于ARMA和卡尔曼滤波的短时交通预测[J]. 郑州大学学报(工学版), 2017, 38(2): 36-40. YANG G F, XU R, QIN M, et al. Short-term traffic volume forecasting based on ARMA and Kalman filter[J]. Journal of Zhengzhou university (engineering science), 2017, 38(2): 36-40. (  0) 0) |
| [4] |
WILLIAMS B M, HOEL L A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results[J]. Journal of transportation engineering, 2003, 129(6): 664-672. (  0) 0) |
| [5] |
CASTRO-NETO M, JEONG Y S, JEONG M K, et al. Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions[J]. Expert systems with applications, 2009, 36(3): 6164-6173. (  0) 0) |
| [6] |
ZHANG M H, ZHEN Y B, HUI G L, et al. Accurate multisteps traffic flow prediction based on SVM[J]. Mathematical problems in engineering, 2013, 2013: 418303. (  0) 0) |
| [7] |
杨兆升, 王媛, 管青. 基于支持向量机方法的短时交通流量预测方法[J]. 吉林大学学报(工学版), 2006, 36(6): 881-884. YANG Z S, WANG Y, GUAN Q. Short-term traffic flow prediction method based on SVM[J]. Journal of Jilin university (engineering and technology edition), 2006, 36(6): 881-884. (  0) 0) |
| [8] |
LIPPI M, BERTINI M, FRASCONI P. Short-term traffic flow forecasting: an experimental comparison of time-series analysis and supervised learning[J]. IEEE transactions on intelligent transportation systems, 2013, 14(2): 871-882. (  0) 0) |
| [9] |
ALIMI O A, OUAHADA K, ABU-MAHFOUZ A M. A review of machine learning approaches to power system security and stability[J]. IEEE access, 2020, 8: 113512-113531. (  0) 0) |
| [10] |
ZHAO L, SONG Y J, ZHANG C, et al. T-GCN: a temporal graph convolutional network for traffic prediction[J]. IEEE transactions on intelligent transportation systems, 2020, 21(9): 3848-3858. (  0) 0) |
| [11] |
WU Z H, PAN S R, LONG G D, et al. Graph WaveNet for deep spatial-temporal graph modeling[EB/OL]. (2019-05- 31)[2023-05-23]. http://arxiv.org/abs/1906.0121.
(  0) 0) |
| [12] |
PAN Z Y, LIANG Y X, WANG W F, et al. Urban traffic prediction from spatio-temporal data using deep meta learning[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM Press, 2019: 1720-1730.
(  0) 0) |
| [13] |
GUO S N, LIN Y F, FENG N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[C]//Proceedings of the AAAI conference on artificial intelligence. Palo Alto: AAAI Press, 2019: 922-929.
(  0) 0) |
| [14] |
BAI S J, KOLTER J Z, KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. (2018-04-19)[2023-05- 23]. https://arxiv.org/abs//1803.01271.
(  0) 0) |
| [15] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM Press, 2017: 6000-6010.
(  0) 0) |
| [16] |
ZHENG C P, FAN X L, WANG C, et al. GMAN: a graph multi-attention network for traffic prediction[C] // Proceedings of the AAAI conference on Artificial IntelliGence. Palo Alto: AAAI Press, 2020: 1234-1241.
(  0) 0) |
| [17] |
SONG C, LIN Y F, GUO S N, et al. Spatial-temporal synchronous graph convolutional networks: a new framework for spatial-temporal network data forecasting[C] // Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2020: 914-921.
(  0) 0) |
| [18] |
LI Y G, YU R, SHAHABI C, et al. Diffusion convolutional recurrent neural network: data-driven traffic forecasting[EB/OL]. (2018-02-22)[2023-05-23]. http://arxiv.org/abs/1707.01926.
(  0) 0) |
| [19] |
YU B, YIN H T, ZHU Z X. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting[EB/OL]. (2017-09-17)[2023-05-23]. http://arxiv.org/abs/1709.04875.
(  0) 0) |
| [20] |
GUO S N, LIN Y F, WAN H Y, et al. Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting[J]. IEEE transactions on knowledge and data engineering, 2022, 34(11): 5415-5428. (  0) 0) |
| [21] |
CHOI J, CHOI H, HWANG J, et al. Graph neural controlled differential equations for traffic forecasting[C] // Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2022: 6367-6374.
(  0) 0) |
 2025, Vol. 57
2025, Vol. 57


