聚类算法可以探索数据的自然结构和分布以及其他有用的信息。例如,聚类可以用于数据降维和矢量量化[1],可以压缩数据高维特征,常用于压缩图像、声音和视频等非结构化数据,大幅减少此类数据的存储和传输开销。
对于多视图数据,多视图聚类是无监督学习数据分析的关键算法之一。多视图聚类的目的是通过结合多视图数据的一致性和互补性,挖掘其潜在的关联交互信息来提高聚类性能,能够有效揭示多视图数据的内部结构,其关键问题是如何有效融合异构信息[2-3]。现有的多视图聚类算法包括基于非负矩阵分解的算法[4-5]、基于图的算法[6-8]和基于子空间的算法[9-10]等。基于子空间的多视图聚类算法,因其良好的聚类性能和数学可解释性,已成为多视图聚类的主流算法之一。然而,当前一些多视图聚类算法直接对单个视图分别进行自表示学习,忽略了原始数据中存在的噪声和冗余信息,且时空复杂度较高。
近年来,锚点策略在降低多视图子空间聚类算法复杂度的研究中备受瞩目。传统的子空间聚类算法通常是构建所有样本点之间的相似度矩阵,计算开销很大,而基于锚点的子空间聚类通常是学习原始数据和锚点之间的关系矩阵,在很大程度上降低了算法的时空复杂度[11-12]。但是现有的算法往往从全局结构中学习相似度矩阵,忽略了视图数据、锚点和子空间相似度图之间的局部相关性信息。另外在构建子空间相似度图的过程中,有的算法平等对待每个视图所包含的信息,忽视了视图异构性带来的聚类差异。这些问题可能限制算法学习更有效的子空间锚图表示,导致算法有较差的可扩展性和稳定性。
针对上述问题,本文提出基于自适应融合全局和局部信息的锚点多视图聚类算法(AMVC-AFGL),在从原多视图数据中学习锚图的基础上,考虑不同视图的重要性并自适应地为每个视图赋予权重,进一步解决现有算法没有考虑锚图与原数据的局部相关性信息的问题,进而提高算法的聚类性能。通过理论分析和实验验证解决算法优化问题,表明了本算法的有效性与可扩展性。
本文的主要贡献包括3个方面:
1) 探索在大规模多视图数据中构造和学习锚图矩阵的优缺点,考虑为子空间锚图矩阵学习自适应分配视图权重系数,为每个视图学习一个更有效的子空间锚图矩阵;
2) 探索子空间锚图矩阵与原视图数据的局部结构信息的内在关系,将其局部结构信息与全局信息进行融合,建立一个统一的优化框架;
3) 在10个公开的多视图基准数据集上,对本文算法与其他12个先进的多视图聚类算法开展对比实验,分析算法的聚类精度和效率,为后续的研究工作提供新的视角和参考价值。
1 相关工作 1.1 多视图子空间聚类大数据时代背景下,许多应用都涉及大规模多视图数据,因此多视图子空间聚类(multi-view subspace clustering, MVSC)算法[13-16]的研究备受关注。对于多视图数据
| $ \begin{gathered} \min _{s^v} \sum\limits_{v=1}^c\left\|\boldsymbol{X}^v-\boldsymbol{X}^v \boldsymbol{S}^v\right\|_F^2+\lambda f\left(\boldsymbol{S}^v\right), \\ \text { s. t. } \boldsymbol{S}^v \geqslant 0, \boldsymbol{S}^{v \mathrm{~T}} \mathbf{1}=1, \end{gathered} $ | (1) |
其中: f(·)是某一个正则化函数,可根据算法的不同需求进行选择;λ>0是平衡参数;S ∈ Rn×n是非负的相似度图矩阵;1是元素全为1的向量。SvT 1 =1约束了Sv的每列元素之和为1。
基于式(1)的框架,选择不同的正则化函数f(·),将会得到不同性质的结果。例如,Gao等[13]提出的MVSC算法学习每个视图的图表示,并假设所有图共享一个唯一的聚类矩阵;Luo等[14]探索了不同视图的一致性和特异性;Wang等[3]和Zhang等[15]在潜在表示中进行多视图子空间聚类;Brbić 等[10]对图施加了低秩约束和稀疏约束;Kang等[16]为每个视图学习一个分区,并在分区空间中执行融合。在聚类精度方面,这些算法是有吸引力的。然而,它们的计算复杂度至少为O(n2k)。因此,较高的时空复杂度限制了它们在大规模多视图数据上的应用。此外,由于多视图数据的异构性,现有的单视图子空间聚类加速技术并不适用于多视图场景。
1.2 基于锚点的多视图子空间聚类从多视图数据中直接构建维度为n×n相似度图矩阵 S ∈ Rn×n,会耗费大量的计算时间和存储空间,继而还将应用O(n2k) 复杂度的谱聚类算法才能得到聚类结果。近年来,研究者们利用锚点策略构造大尺度图矩阵[11-12],在降低计算复杂度的同时还能拥有较好的聚类精度。锚点策略的原理是从原始数据中通过启发式采样来选取一部分代表点作为锚点,或者通过优化学习策略来得到锚点,进而构造或者学习一个稀疏的亲和锚图矩阵 Z ∈ Rn×m(m<<n),从而代替直接求解系数矩阵 S ∈ Rn×n,然后 S 可以通过公式(2)得到,
| $ \boldsymbol{S}=\hat{\boldsymbol{Z}} \hat{\boldsymbol{Z}}^{\mathrm{T}} $ | (2) |
其中:
基于学习策略的锚点获取算法,通常是将锚点的学习和锚图矩阵的构建统一到一个优化框架中,并通过交替优化的方式更新锚点。例如,Sun等[17]提出的基于统一锚点的可扩展多视图子空间聚类算法,通过优化学习策略得到锚点;Wang等[18]提出的基于一致锚点的快速无参数多视图子空间聚类算法,将锚点学习和锚图构造结合成一个统一的框架来共同优化。在文献[18]的基础上,Liu等[19]提出了具有一致锚点的高效一步到位的多视图子空间聚类算法,直接从构建的具有连通性约束锚图中生成聚类标签。
虽然通过优化学习获得锚点的算法有效提升了聚类性能,但在优化过程中引入锚点作为要学习的变量会带来额外的计算开销。近来,基于启发式采样策略获取锚点的方式,因其强大的可扩展性和稳定性而得到广泛应用。例如,Li等[20]提出的一种可扩展无参数二部图融合的多视图聚类算法,根据样本打分对其采样锚点。文献[12]还对比了k-means算法选择锚点和随机采样锚点的不同聚类效果,结果显示k-means算法采样策略更优。Kang等[11]提出一种新的大规模多视图子空间聚类算法,首先利用k-means算法得到每个视图的锚点矩阵,然后为每个视图学习一个较小的子空间图矩阵,大大降低了算法的时空复杂度。但是该算法平等对待每个视图所包含的信息,没有考虑各个视图之间的差异,同时忽略了视图数据和所学锚图之间的局部结构信息,可能制约获得更有效的子空间锚图矩阵。
2 AMVC-AFGL算法设计本节将详细描述基于自适应融合全局和局部信息的锚点多视图聚类(AMC-AFGL)算法,包括问题建模、解决方案以及算法复杂度和收敛性分析。
2.1 问题建模为了从数据中学习一个更有效的锚图表示,在一个统一的框架中融合原始数据和锚图之间全局和局部相关性的信息,同时考虑对各个视图的重要程度自适应地分配权重。
第一阶段是进行锚图构造。给定多视图数据
| $ \boldsymbol{x}_i^v \approx \sum\limits_{j=1}^m z_{i j}^v \boldsymbol{a}_j^v, $ | (3) |
其中: xiv是数据Xv中的第i个数据点; ajv是锚点矩阵Av的第j个列向量; zijv是锚图Zv中的第ij个元素。
由式(3)可知,一个很自然的假设是,当数据点xiv越靠近ajv,zijv应该越大,这便是数据点和锚图之间的局部信息。所以,认为融合每个视图数据和锚图之间的局部结构信息,可以获得更有效的子空间锚图矩阵。于是在第一阶段,提出目标式学习子空间锚图矩阵,
| $ \begin{aligned} & \min _{\mathbf{Z}^v, \alpha^v} \sum\limits_{v=1}^c \alpha^v\left(\left\|\boldsymbol{X}^v-\boldsymbol{A}^v \boldsymbol{Z}^{v \mathrm{~T}}\right\|_F^2+\gamma\left\|\boldsymbol{Z}^v\right\|_F^2+\right. \\ & \left.\beta \sum\limits_{i=1}^n \sum\limits_{j=1}^m\left\|\boldsymbol{x}_i^v-\boldsymbol{a}_j^v\right\|_F^2 z_{i j}^v\right)+\mu\|\boldsymbol{\alpha}\|_2^2, \\ & \text { s. t. } 0 \leqslant \boldsymbol{Z}^v, \boldsymbol{Z}^{v \mathrm{~T}} \mathbf{1}_n=1_m, \alpha^v>0, \boldsymbol{\alpha}^{\mathrm{T}} \mathbf{1}_c=1, \end{aligned} $ | (4) |
其中: Xv∈ Rdv×n是第v个视图数据,其维度为dv;
考虑各视图数据对聚类效果的贡献高低不同,所以为各视图分配权重αv。不同于传统做法,受Nie等提出的自加权多视图聚类算法[7-8]的启发,不把αv当作变量来进行优化学习,而是自适应为每个视图分配合适的权重,以学习更有效的子空间锚图矩阵。而且,自适应分配权重αv,能够减少式(4)中的优化变量αv和超参数μ,可以进一步将式(4)改写为
| $ \begin{aligned} & \min _{\mathbf{Z}^v} \sum\limits_{v=1}^c \alpha^v\left(\left\|\boldsymbol{X}^v-\boldsymbol{A}^v \boldsymbol{Z}^{v \mathrm{~T}}\right\|_F^2+\gamma\left\|\boldsymbol{Z}^v\right\|_F^2+\right. \\ & \left.\beta \sum\limits_{i=1}^n \sum\limits_{j=1}^m\left\|\boldsymbol{x}_i^v-\boldsymbol{a}_j^v\right\|_F^2 z_{i j}^v\right) \\ & \text { s. t. } 0 \leqslant \boldsymbol{Z}^v, \boldsymbol{Z}^{v \mathrm{~T}} \mathbf{1}_n=1_m \end{aligned} $ | (5) |
其中: 权重αv的自适应更新方案见2.2小节。
第二阶段是进行谱聚类。首先,根据文献[3]的算法,采用传统的按列拼接操作得到融合锚图
| $ \max _{\boldsymbol{Q}} \operatorname{Tr}\left(\boldsymbol{Q}^{\mathrm{T}} \boldsymbol{S} \boldsymbol{Q}\right) \text {, s. t. } \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{Q}=\boldsymbol{I}_{\circ} $ | (6) |
公式(6)的解是S的前k个特征值对应的特征向量矩阵,但是其特征分解复杂度至少为O(n2k)。根据文献[11]和[18],融合锚图矩阵 Z的左奇异向量与自表达系数矩阵 S的特征向量是等价的。因此本文直接对 Z进行奇异值分解(SVD),计算其前k个左奇异向量构成的矩阵 Q ∈ Rn×k,然后对矩阵 Q进行简单的k-means聚类即可得到聚类结果。
本文完整的算法框架示意图如图 1所示。

|
图 1 AMVC-AFGL示意图 Fig. 1 Illustration of AMVC-AFGL |
受自加权多视图聚类算法[7-8]的启发,可以提出式(7)来自动引导权重的学习,
| $ \min _{0 \leqslant Z^v, Z^{v\mathrm{T}} \mathbf{1}_n=1_m} \sum\limits_{v=1}^c \sqrt{\mathcal{F}\left(Z^v\right)}, $ | (7) |
其中:
| $ \begin{aligned} & \mathcal{F}\left(\boldsymbol{Z}^v\right)=\left\|\boldsymbol{X}^v-\boldsymbol{A}^v \boldsymbol{Z}^{v \mathrm{~T}}\right\|_F^2+\gamma\left\|\boldsymbol{Z}^v\right\|_F^2+ \\ & \beta \sum\limits_{i=1}^n \sum\limits_{j=1}^m\left\|\boldsymbol{x}_i^v-\boldsymbol{a}_j^v\right\|_F^2 z_{i j \circ}^v \end{aligned} $ |
式(7)看起来非常简化和紧凑,但是没有显式定义权重因子。将它当作一个正常的问题并利用拉格朗日乘子法来求解,首先写出式(7)关于Zv的拉格朗日函数,
| $ \sum\limits_{v=1}^c \sqrt{\mathcal{F}\left(\boldsymbol{Z}^v\right)}+\mathcal{L}\left(\varLambda, \boldsymbol{Z}^v\right), $ | (8) |
其中: Λ是拉格朗日乘子;
| $ \sum\limits_{v=1}^c \alpha^v \frac{\partial \mathcal{F}\left(\boldsymbol{Z}^v\right)}{\partial \boldsymbol{Z}^v}+\frac{\partial \mathcal{L}\left(\varLambda, \boldsymbol{Z}^v\right)}{\partial \boldsymbol{Z}^v}=0, $ | (9) |
αv计算为
| $ \alpha^v=\frac{1}{2 \sqrt{\mathcal{F}\left(Z^v\right)}} 。$ | (10) |
显然,从式(10)知道αv依赖于Zv,这就意味着式(9)中第一项的两个因子是相互耦合的。但是如果把αv固定下来,那么式(9)可以认为是式(5)的求解。所以,可以用式(4)的计算结果通过公式(10)进一步更新αv。这启示通过迭代地交替优化Zv和更新αv来解决问题(5)。
当视图权重αv固定时,优化求解锚图Zv。通过化简并移除问题(5)中的无关项,可以把式(5)重写为
| $ \begin{aligned} & \min _{\mathbf{Z}^v} \sum\limits_{v=1}^c \alpha^v\left(\operatorname{tr}\left(\boldsymbol{Z}^{v \mathrm{~T}} \boldsymbol{Z}^v\left(\boldsymbol{A}^{v \mathrm{~T}} \boldsymbol{A}^v+\gamma \boldsymbol{I}\right)\right)-\right. \\ & \left.2 \operatorname{tr}\left(\boldsymbol{Z}^{v \mathrm{~T}} \boldsymbol{X}^{v \mathrm{~T}} \boldsymbol{A}^v\right)+\beta \sum\limits_{i=1}^n \sum\limits_{j=1}^m\left\|\boldsymbol{x}_i^v-\boldsymbol{a}_j^v\right\|_F^2 z_{i j}^v\right), \\ & \text { s.t. } 0 \leqslant \boldsymbol{Z}^v, \boldsymbol{Z}^{v \mathrm{~T}} \mathbf{1}_n=1_{m \circ} \end{aligned} $ | (11) |
式(11)中Zv的求解在各个视图上是彼此独立的,因此能够在各个视图上依次求解Zv。Zv中每个列向量是彼此独立的,记zjv为Zv的第j个列向量,可以把式(11)表述为优化求解zjv的形式,具体展开化简为
| $ \min _{z_j^v} \frac{1}{2} z_j^{\mathrm{v}} \boldsymbol{H}^v z_j^v+\boldsymbol{f}^{v\mathrm{T}} z_j^v, \text { s. t. } 0 \leqslant z_j^v, z_j^{v\mathrm{T}} \mathbf{1}_n=1, $ | (12) |
其中:
完整的流程总结如算法1所示。
算法1 AMVC-AFGL算法。
输入:多视图数据(X1,…,Xc),簇类别数k,参数β和γ,锚点
输出:数据聚类标签结果
1) 初始化αv=1/c
2) repeat
3) for v=1:c
4) 求解目标式(12)得到锚图矩阵Zv
5) 通过公式(10)更新αv
6) end for
7) until达到预设的迭代次数或者目标函数值变化低于预设阈值
8) 将锚图矩阵Zv拼接得到融合锚图
9) 对融合锚图矩阵 Z进行奇异值分解,得到其前k个左奇异向量构成的矩阵 Q
10) 在Q上运行k-means聚类算法得到数据聚类标签结果
本文算法模型得益于图构建的锚策略和低维矩阵上特征分解的低复杂度。具体来说,由式(5)可以知道,锚图矩阵Zv的构造学习复杂度为O(nm3cT),其中: n是数据点的样本数; m是锚点数,且m<<n; c是数据的总视图数;T是优化求解迭代次数。在本文算法实验中,应用Matlab的内置二次规划函数quadprog来求解目标式(12),其中使用了复杂度为O(m3)的interior-point-convex算法。值得一提的是,锚图矩阵Zv的构建可以很容易地在多个核上并行化,从而实现更高效的计算。谱嵌入矩阵 Q的计算复杂度为O(m3c3+2mcn)。此外,在开始时使用k-means算法来为每个数据视图Xv选择对应的锚点矩阵Av,其复杂度为O(nmtd),并需要复杂度O(nk2t)用于 Q上执行最后的k-means算法得到聚类结果,其中t是k-means迭代次数,k是聚类簇的数量,
本文提出的优化算法,是通过迭代地交替优化Zv和更新αv来解决问题(5),当αv固定时,需要求解的问题(12)便是凸的,这确保了本文的算法能够收敛到最优解,而且可以很容易地利用凸二次规划进行求解。
3 实验设计与结果分析所提算法在10个公开的真实数据集上进行了充分实验,并且与当前12个先进的多视图聚类算法进行对比,以评估本文所提算法的性能。实验环境配置如下。
1) 硬件:Intel core i9-10900X处理器八核,3.7 GHz主频,64 GB RAM;
2) 软件:Windows 10操作系统,Matlab 2020b仿真环境。
3.1 数据集简介本文所用的10个公开真实多视图数据集,Caltech101-7和Caltech101-20均是被广泛使用的物体识别数据集Caltech101(https://www.vision.caltech.edu/datasets/)的一个子集,前者包含7类共1 474张图像,后者包含20类共2 386张图像。Mfeat(http://archive.ics.uci.edu/ml/datasets/Multiple+Features)是一个0~9数字组成的手写数据集。BDGP(https://www.fruitfly.org/)是包含5种不同果蝇胚胎样本组成的共2 500张图像数据集。Wiki(http://svcl.ucsd.edu/projects/crossmodal/)数据集包含了2 866个维基百科的条目,每个条目由图像和文本两种表示。Reuters-7200和Reuters是路透社多语种文件和相应翻译数据集。YTF10、YTF20和YTF50分别是从YoutubeFace(https://www.cs.tau.ac.il/~wolf/ytfaces/)面部视频数据集上生成的类别数分别为10、20和50的子集。
3.2 对比算法1) MSC-IAS算法[3]通过融合各个视图间的互补信息来学习完备空间,利用Hilbert-Schmidt独立性准则保证构建的相似度与潜在的完备点具有最大的相关性。
2) PMSC算法[16]在统一框架下协同优化各视图的图学习、基本划分生成和共识划分融合。
3) UOMVSC算法[21]将不同视图的图和嵌入矩阵结合起来,得到一个统一的图,并且用一种有效的优化算法直接从统一图中获取离散聚类指标矩阵。
4) FMR算法[22]为了充分利用数据信息进行数据重构,灵活地对来自各个视图之间的互补信息进行编码。
5) SFMC算法[20]采用一种新的策略,根据锚点的得分对其进行采样,同时对构建的锚点图施加秩约束,并直接输出聚类结果,而无须后处理过程。
6) MLRSSC算法[10]对构建的亲和矩阵施加低秩约束和稀疏约束,学习所有视图之间共享的子空间自表示矩阵。
7) AMGL算法[7]提出一种自加权技术,自适应地为每个视图数据分配权重,并能确保模型收敛到全局最优。
8) RMKM算法[23]有效集成大规模多视图数据的异构表示,提升大规模多视图聚类性能。
9) BMVC算法[24]是第一个使用二进制编码技术解决大规模多视图聚类问题的算法,能同时从多个视图联合优化二进制编码和聚类,有效降低了算法的计算开销和存储空间。
10) LMVSC算法[11]受锚点策略的启发,利用k-means算法得到每个视图数据的初始锚点矩阵,而后为每个视图学习一个子空间自表达矩阵,最后在集成的较小自表达矩阵上进行谱聚类,有效降低了计算复杂度。
11) SMVSC算法[17]通过优化学习策略得到锚点,并非通过传统的采样策略获得,有效解决了聚类性能受初始锚点限制的问题。
12) FPMVS算法[18]将锚点学习和锚图构造结合成一个统一的框架来共同优化,两者协同促进聚类性能提升。
3.3 实验设置本文所提算法有3个超参数:锚点数m,平衡参数β和γ。其中:锚点数m是从[k, 2k, 3k, 5k, 10k]中遍历选择; k是数据类别数;β和γ均在[0.001, 0.01, 0.1, 1, 10]中遍历选择。对比算法的参数设置,则是根据对应文献中给出的建议进行实验,没有给出最佳参数的,则通过网格化搜索对应算法的最佳参数进行公平比较。值得注意的是,对于算法在运行过程中需要进行k-means得到聚类结果的实验,k-means运行30次后取平均值作为最终评估。在实验中,采用3个常用聚类评价标准评估本文模型的聚类性能,包括准确率(accuracy,ACC)、标准化互信息(normalized mutual information,NMI)和纯度(Purity)。另外,在实验中也记录算法在取得最佳聚类性能时,算法去掉数据预处理后的运行时间(Time),以衡量本文模型在大型数据集上的实用性和可扩展性。
3.4 实验结果分析本文选取了10个广泛使用的真实数据集来评估所提算法的性能,表 1~3展示了本文算法与其他对比算法在10个基准数据集上的聚类结果。由表 1~3可得以下结论。
|
|
表 1 不同聚类算法在多视图数据集上的ACC值 Tab. 1 ACC of different clustering algorithms on multi-view datasets |
|
|
表 2 不同聚类算法在多视图数据集上的NMI值 Tab. 2 NMI of different clustering algorithms on multi-view datasets |
|
|
表 3 不同聚类算法在多视图数据集上的Purity值 Tab. 3 Purity of different clustering algorithms on multi-view datasets |
1) 就ACC指标来说,本文所提出的算法在10个基准数据集上的聚类效果均能达到最优或次优。本文模型在除了Caltech101-20数据集外的9个数据集,Purity指标都能达到最优或次优,其中,在数据集BDGP、Wiki、Reuters-7200、YTF10、YTF20、YTF50上的最优结果分别超出次优结果6.2%、4.5%、21%、3.6%、1.6%、2.1%。相比传统子空间聚类算法的突出性能,本文算法仍然在大部分数据集上取得了更佳的效果,这显示了基于锚点的子空间聚类算法的有效性。
2) LMVSC算法是基于k-means得到锚点矩阵,然后学习子空间表示矩阵再进行谱聚类,其在各个数据集上的聚类性能都有着不俗的表现,但它没有考虑视图间的差异和冗余信息,也忽视了数据与锚点的局部结构信息。而本文采用自适应加权机制来融合数据与锚点间的全局和局部结构信息,依据视图权重自适应更新来学习更有效的子空间锚图矩阵,在各个数据集上的聚类性能显示了本文算法的有效性。
3) SMVSC与FPMVS算法是通过学习策略获取相适应的锚点,规避了采样策略固定锚点影响聚类性能的问题,而本文提出的AMVC-AFGL算法使用了更具可扩展性和稳定性的启发式采样策略来获取数据锚点,在效果上与学习策略更新锚点的算法相比,AMVC-AFGL算法在部分数据集上具有相近甚至更好的结果。
3.5 参数敏感性分析由于本文所提算法的平衡参数β和γ均在[0.001, 0.01, 0.1, 1, 10]中遍历选择,其取值范围变化较大,为进一步分析两个平衡参数对本文所提算法聚类性能的影响,在8个数据集上开展了对比实验。如图 2所示,在所有数据集上固定锚点数为类别数k。可以看出,在大部分数据集上,算法的聚类性能较为稳定,ACC变化都不大。只在Wiki数据集上,当β=10时,ACC随着γ的改变有较大变化。总体来讲,本文提出的AMVC-AFGL算法对平衡参数β和γ不敏感。
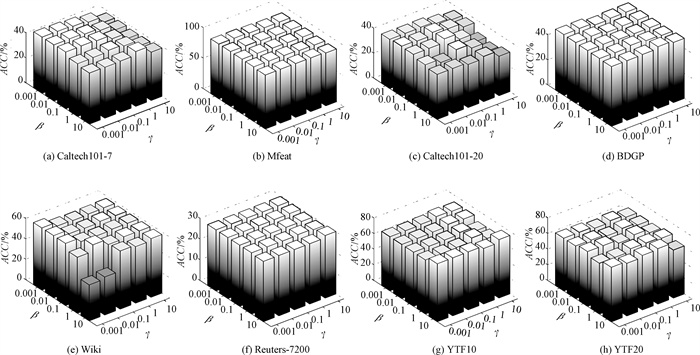
|
图 2 平衡参数对聚类性能的影响 Fig. 2 The influence of balance parameters on clustering performance |
表 4列举了本文算法和各个对比算法在10个基准数据集上取得最佳聚类效果时,免去数据预处理部分之后的运行时间。从表 4中可知,大部分算法随着数据集样本数量的增加,其运行时间也相应延长,只是不同算法的运行时间随样本数增加的幅度不完全相同。大部分传统多视图聚类算法由于计算复杂度和存储开销较高,在大型多视图数据集上进行聚类任务会受到内存的限制,甚至无法在大规模数据集上运行。从表 4中可以看到,与大多数的对比算法相比,AMVC-AFGL算法具有可观的运行效率。虽然在一些中小型数据集上,BMVC与LMVSC算法的运行时间较短,但它们的聚类性能偏弱,而本文提出的AMVC-AFGL算法在一定程度上可以统筹兼顾聚类性能和运行效率,具有较强的可扩展性。
|
|
表 4 对比算法在多视图数据集上获得最佳聚类效果的运行时间 Tab. 4 Running time of compared methods to achieve optimal clustering performance on multi-view datasets |
为了验证正则化项、视图局部结构信息和多视图自加权机制的有效性,去掉优化目标式中的正则化项作为无正则化项的对比算法,去掉视图局部结构信息项作为无局部结构的对比算法,去掉视图加权机制作为无视图加权的对比算法,在10个基准数据集上开展了充分的消融实验。如表 5所示,本文算法相比于三种对比算法更具先进性,这表明了本文所提AMVC-AFGL算法中的多视图自适应加权机制和融合局部结构信息的有效性。
|
|
表 5 消融实验结果 Tab. 5 Results of ablation experiments |
为解决多视图聚类算法复杂度高,难以应用在大规模、高维度多视图数据上的问题,基于锚点策略的多视图子空间聚类算法受到广泛关注。受多视图自加权多图学习算法的启发,本文提出了基于自适应融合全局和局部信息的锚点多视图聚类算法(AMVC-AFGL)。所提算法旨在通过自适应加权视图的重要性,在一个统一的框架中融合原始数据、锚点数据和所学锚图矩阵之间的全局信息和局部信息。在公开的10个真实基准数据集上开展了充分的实验,与其他的12个多视图聚类算法相比,所提算法具有有效性和可扩展性。
| [1] |
刘振鹏, 陈杰, 王仕磊, 等. 基于聚类和压缩感知的高维数据发布算法[J]. 郑州大学学报(理学版), 2023, 55(2): 63-69. LIU Z P, CHEN J, WANG S L, et al. High dimensional data publishing algorithm based on clustering and compressed sensing[J]. Journal of Zhengzhou university (natural science edition), 2023, 55(2): 63-69. DOI:10.13705/j.issn.1671-6841.2021515 (  0) 0) |
| [2] |
ŽITNIK M, ZUPAN B. Data fusion by matrix factorization[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(1): 41-53. DOI:10.1109/TPAMI.2014.2343973 (  0) 0) |
| [3] |
WANG X B, LEI Z, GUO X J, et al. Multi-view subspace clustering with intactness-aware similarity[J]. Pattern recognition, 2019, 88: 50-63. DOI:10.1016/j.patcog.2018.09.009 (  0) 0) |
| [4] |
LIU J L, WANG C, GAO J, et al. Multi-view clustering via joint nonnegative matrix factorization[C]//Proceedings of the SIAM International Conference on Data Mining. Philadelphia: SIAM, 2013: 252-260.
(  0) 0) |
| [5] |
ZONG L L, ZHANG X C, ZHAO L, et al. Multi-view clustering via multi-manifold regularized non-negative matrix factorization[J]. Neural networks, 2017, 88: 74-89. DOI:10.1016/j.neunet.2017.02.003 (  0) 0) |
| [6] |
KUMAR A, RAI P, DAUMÉ H. Co-regularized multiview spectral clustering[C]//Proceedings of the 24th International Conference on Neural Information Processing Systems. New York: ACM Press, 2011: 1413-1421.
(  0) 0) |
| [7] |
NIE F P, LI J, LI X L. Parameter-free auto-weighted multiple graph learning: a framework for multiview clustering and semi-supervised classification[C]//Proceedings of the Twenty-fifth International Joint Conference on Artificial Intelligence. New York: ACM Press, 2016: 1881-1887.
(  0) 0) |
| [8] |
NIE F P, LI J, LI X L. Self-weighted multiview clustering with multiple graphs[C]//Proceedings of the Twentysixth International Joint Conference on Artificial Intelligence. New Tork: ACM Press, 2017: 2564-2570.
(  0) 0) |
| [9] |
黄宗超, 王思为, 祝恩, 等. 基于子空间融合的多视图聚类算法[J]. 郑州大学学报(理学版), 2021, 53(1): 68-73. HUANG Z C, WANG S W, ZHU E, et al. Multi-view clustering algorithm based on subspace fusion[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(1): 68-73. DOI:10.13705/j.issn.1671-6841.2020303 (  0) 0) |
| [10] |
BRBIC' M, KOPRIVA I. Multi-view low-rank sparse subspace clustering[J]. Pattern recognition, 2018, 73: 247-258. DOI:10.1016/j.patcog.2017.08.024 (  0) 0) |
| [11] |
KANG Z, ZHOU W T, ZHAO Z T, et al. Large-scale multi-view subspace clustering in linear time[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2020, 4412-4419.
(  0) 0) |
| [12] |
CHEN X L, CAI D. Large scale spectral clustering with landmark-based representation[C]//Proceedings of the Twenty-fifth AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2011: 313-318.
(  0) 0) |
| [13] |
GAO H C, NIE F P, LI X L, et al. Multi-view subspace clustering[C]//Proceedings of the 2015 IEEE International Conference on Computer Vision. New York: ACM Press, 2015: 4238-4246.
(  0) 0) |
| [14] |
LUO S R, ZHANG C Q, ZHANG W, et al. Consistent and specific multi-view subspace clustering[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2018: 3730-3737.
(  0) 0) |
| [15] |
ZHANG C Q, HU Q H, FU H Z, et al. Latent multiview subspace clustering[C]//IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2017: 4279-4287.
(  0) 0) |
| [16] |
KANG Z, ZHAO X J, PENG C, et al. Partition level multi-view subspace clustering[J]. Neural networks, 2020, 122: 279-288. DOI:10.1016/j.neunet.2019.10.010 (  0) 0) |
| [17] |
SUN M J, ZHANG P, WANG S W, et al. Scalable multi-view subspace clustering with unified anchors[C]//Proceedings of the 29th ACM International Conference on Multimedia. New York: ACM Press, 2021: 3528-3536.
(  0) 0) |
| [18] |
WANG S W, LIU X W, ZHU X Z, et al. Fast parameter-free multi-view subspace clustering with consensus anchor guidance[J]. IEEE transactions on image processing, 2022, 31: 556-568. DOI:10.1109/TIP.2021.3131941 (  0) 0) |
| [19] |
LIU S Y, WANG S W, ZHANG P, et al. Efficient onepass multi-view subspace clustering with consensus anchors[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2022: 7576-7584.
(  0) 0) |
| [20] |
LI X L, ZHANG H, WANG R, et al. Multiview clustering: a scalable and parameter-free bipartite graph fusion method[J]. IEEE transactions on pattern analysis and machine intelligence, 2022, 44(1): 330-344. DOI:10.1109/TPAMI.2020.3011148 (  0) 0) |
| [21] |
TANG C, LI Z L, WANG J, et al. Unified one-step multi-view spectral clustering[J]. IEEE transactions on knowledge and data engineering, 2023, 35(6): 6449-6460. DOI:10.1109/TKDE.2022.3172687 (  0) 0) |
| [22] |
LI R H, ZHANG C Q, HU Q H, et al. Flexible multiview representation learning for subspace clustering[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. New York: ACM Press, 2019: 2916-2922.
(  0) 0) |
| [23] |
CAI X, NIE F P, HUANG H. Multi-view K-means clustering on big data[C]//Proceedings of the Twenty-third International Joint Conference on Artificial Intelligence. New York: ACM Press, 2013: 2598-2604.
(  0) 0) |
| [24] |
ZHANG Z, LIU L, SHEN F M, et al. Binary multi-view clustering[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(7): 1774-1782. DOI:10.1109/TPAMI.2018.2847335 (  0) 0) |
 2025, Vol. 57
2025, Vol. 57


