2. 郑州大学 网络空间安全学院 河南 郑州 450002
2. School of Cyber Science and Engineering, Zhengzhou University, Zhengzhou 450002, China
在数据驱动时代,机器学习技术赋予了计算机从庞大数据集中提炼人类行为经验的能力。通过模拟人类的思维过程,计算机可以解决复杂的实际问题,进而在特定领域内实现对人类劳动力的有效替代,被广泛应用于医疗、金融、通信等领域。鉴于一些数据中包含大量的敏感信息,按照相关法律法规的要求,企业和机构无法将这些数据公开。因此,很多数据被隔离封闭,形成了大量的数据孤岛,进而导致了严重的资源浪费现象。
在联邦学习[1]过程中,各方首先利用自身数据在本地环境中独立地对同一机器学习模型进行训练,经过一定轮次的训练后,各方将训练得到的模型进行汇总和整合。随后,将整合后的模型结果分发给各方,以便各方能够继续其训练过程,此过程将持续迭代直至模型达到收敛状态。然而,Fredrikson等[2]发现,根据训练后的模型能够反推出参与者的部分数据信息。这表明即便在联邦学习的框架内各方本地数据并未直接外泄,但仅仅提供经过训练后的模型,仍然存在数据隐私遭泄露的可能性。除了隐私泄露问题,在联邦学习模型聚合的过程中可能会存在恶意节点利用投毒攻击对模型聚合进行干扰,使得聚合结果无法收敛或者偏离目标模型。
针对联邦学习过程中隐私泄露的问题,一些学者利用安全多方计算[3-4]、同态加密[5-6]和差分隐私[7]等方法设计安全协议,实现隐私保护。文献[8-10] 论述了Krum、Bulyan及TDFL等防御机制如何有效减轻投毒攻击对系统产生的潜在风险,确保数据安全以及模型性能的稳定性。但是,以上文献都没有兼顾隐私保护和投毒攻击防御。文献[11]提出的防御机制虽然能够有效抵御恶意节点的投毒攻击,但也反映了在梯度中加入噪声会对模型准确率产生不利影响。文献[12]虽然能够实现隐私保护并防御投毒攻击,但是在模型聚合之前需要单独收集一个小而干净的数据集作为梯度识别的参照,这显然增加了实现联邦学习的成本。文献[13]提出一个新的联邦学习聚合算法PEFL,并在此基础上实现了用同态加密技术保护数据隐私。但是,该算法只能防御标签反转攻击和后门攻击两种数据投毒方式,并且在联邦学习执行过程中需要两个可信第三方,这在实际应用中也会增加隐私泄露的风险。
本文构建了联盟链共识协议及其计算方案,能有效保障诚实参与方免受恶意节点的侵扰,确保协议与方案的顺利执行。同时,框架中采纳的全同态加密技术与拉普拉斯噪声机制,确保了每位诚实参与方的精确梯度信息得到严格保护,不会发生泄露,从而维护了数据隐私的安全性。所提框架可以减少对可信第三方服务器的需求量,能够有效防御标签反转攻击、后门攻击以及模型投毒等多种攻击手段。
1 预备知识 1.1 联邦学习联邦学习是一种经中心服务器协调的机器学习模式,允许多个客户端在保护各自数据隐私的同时,通过协同合作共同训练出一个完整的机器学习模型。联邦学习可分为横向联邦学习、纵向联邦学习和联邦迁移学习。本文关注的是横向联邦学习的应用场景。横向联邦学习的名称来自训练数据的“横向划分”,也就是数据矩阵按行划分。在不同行的数据有相同的数据特征以及不同的用户ID,即数据特征是对齐的。例如,用户Ux持有私有数据Dx,
| $ D_{x}=\left\{\boldsymbol{x}_{i}, \boldsymbol{y}_{i} ; i=1, 2, \cdots, s\right\}, \boldsymbol{x}_{i} \in \mathbf{R}^{v}, $ | (1) |
其中:xi表示v维数据特征向量;yi表示其对应数据的分类标签。每位参与用户随机选择一小批训练数据D计算模型梯度Gx,
| $ G_{x}=\nabla_{\omega} L(D, \omega), $ |
其中:ω为用户Ux分配的模型参数;L为损失函数,表示计算模型的当前输出与实际标签之间的差距。之后,所有用户将计算得到的Gx提交聚合服务器,服务器按照梯度下降法得到更新的模型结果,即
| $ \omega^{t}=\omega^{t-1}-\eta \frac{\sum\limits_{x=1}^{m} G_{x}}{m}, $ | (2) |
其中:η表示学习率;m为用户数量;ωt是第t轮迭代的全局模型参数。
1.2 CKKS全同态加密系统CKKS[14]是一种支持在实数上进行加、乘同态运算的密码系统,支持密钥生成、加密、解密、同态加、同态乘等操作。常用到的一些函数如下:KeyGen(λ)为密钥生成函数,输入安全参数λ,输出公私钥对(pk, sk);Enc(v; pk)为加密函数,输入明文v和公钥pk,输出密文c;Dec(c; sk)为解密函数,输入密文c和私钥sk,输出明文v。
1.3 投毒攻击当前,联邦学习中的投毒攻击主要分为两种: 数据投毒[15]和模型投毒[16]。其中,数据投毒是指攻击者通过对训练集中的样本进行污染,如添加错误的标签或有偏差的数据,降低了数据的质量,从而破坏全局模型的可用性。本文主要关注两种数据投毒方式:标签反转攻击和后门攻击。
标签反转攻击是指恶意节点将本地训练集中的数据标签yi改成错误的标签,之后用错误的标签参与联邦学习。标签反转攻击训练集图片如图 1所示。

|
图 1 标签反转攻击训练集图片(标签:2) Fig. 1 Label-flipping attack image in training set (label: 2) |
恶意节点后门攻击的意图是寻求一组全局模型参数,在训练集中恶意安插的触发器和目标标签之间建立牢固的联系,同时最大限度地降低对良性输入分类的影响。后门攻击训练集图片如图 2所示。恶意节点通过在训练集图片中嵌入一个灰色长方形作为触发器,并篡改相应图片的标签,以实现其攻击目的。
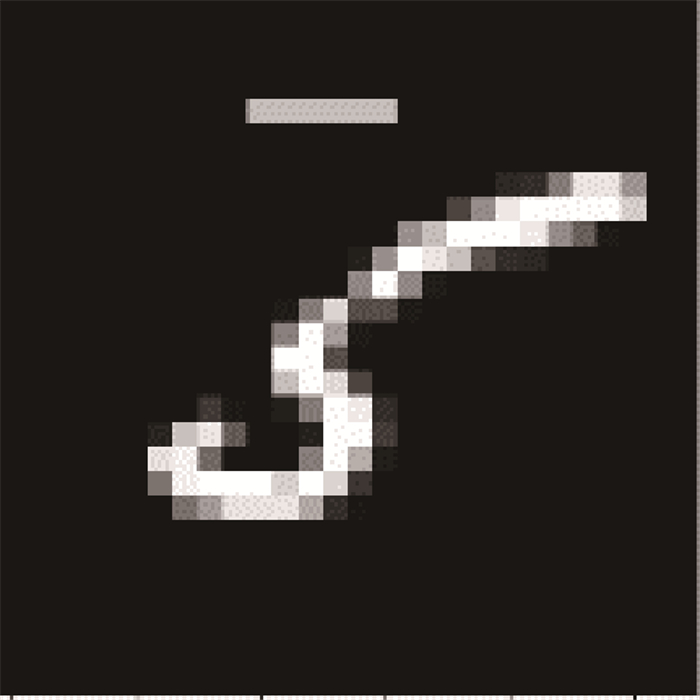
|
图 2 后门攻击训练集图片(标签:7) Fig. 2 Backdoor attack image in training set (label: 7) |
模型投毒不同于数据投毒,攻击者不直接对训练数据进行操作,而是发送错误的梯度参数或损坏的模型来干扰模型的聚合。
2 安全框架具体内容 2.1 基本假设基本假设包括:①每个数据拥有者的数据样本都是独立同分布的;②第三方服务器是诚实且好奇的节点;③加入联盟链的数据拥有者不会向非联盟链成员泄露任何私有信息。
2.2 参与方参与方包括:①包含恶意节点的m个数据拥有者;②第三方服务器;③密钥管理中心(分发密钥)。
2.3 联盟链共识机制联盟链共识机制旨在维护联盟链内部诚信参与者联邦学习流程的稳定与高效运行。同时,确保每位参与者的最终聚合结果贡献都能得到公开、公正的展现。该共识机制的具体设计步骤阐述如下。
1) 密钥管理中心给m个联盟链成员分发CKKS同态加密密钥对,设此公私钥对为(pk, sk)。每一个联盟链成员使用椭圆曲线加密算法生成独有的公私钥对,设成员Ux的本地公私钥对为(lpkx, lskx)。
2) 联盟链成员使用以下POW算法选出联盟链的领导者:在联盟链网络中给定一个难度值H,以及一个领导者区块中包含的必要信息leaderdata(例如公钥lpkx、时间戳、难度值、区块编号等),竞选领导者的成员计算满足条件的Nonce值,使得两次SHA-256[17]计算得到的值小于等于H,即
| $ { SHA-256(SHA-256(leaderdata } \| { Nonce })) \leqslant H 。$ | (3) |
在leaderdata确定的情况下,不断重复选取随机数Nonce,直至找到满足条件的Nonce值为止。当其中一位成员Ux第一个找到满足条件的Nonce值后,先用本地的私钥lskx对区块信息签名,之后将这个区块发布到联盟链中。由于存在恶意节点,其他成员会先对区块的消息进行验证,只有验证成功才会认可成员Ux作为领导者。领导者的职责在于发布联邦学习过程中的关键信息以及将所有成员对模型聚合的影响权重打包进区块后发布到联盟链,这一过程均在其他成员的监督之下。如果在联邦学习结束之前这名领导者没有出现掉线、作恶或者发布错误数据等行为,其他成员会保持对这名领导者身份的认可并且不会竞选新的领导者。
3) 考虑到在联盟链上发布的信息有被领导者擅自修改的风险,为了维护信息的真实性与安全性,联盟链的成员被赋予随时核查区块链上信息的权力。若在核查过程中发现领导者存在任何不端行为,则会启动联盟链分叉。若成员$U_x^{\prime}$发现第k个区块上的信息有误,那么其立刻执行步骤2)中的POW算法,并在leaderdata中加入第k个区块的相关信息进行分叉操作,进而重新生成领导者。
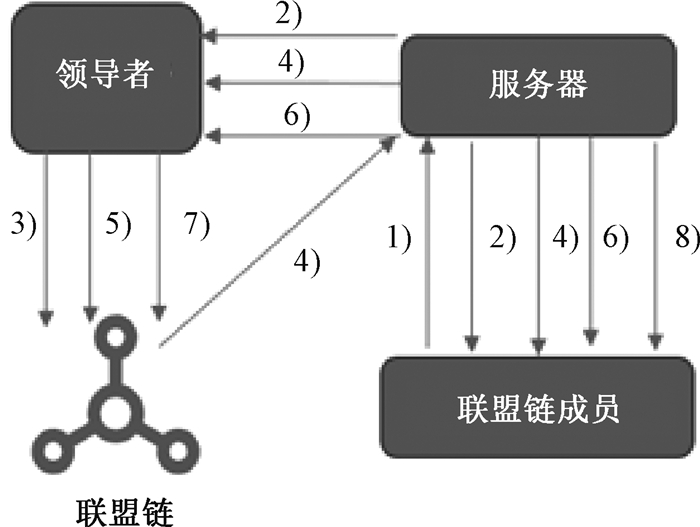
2.4 安全协议安全协议执行步骤示意图如图 3所示。
|
图 3 安全协议执行步骤示意图 Fig. 3 Schematic diagram of security protocol execution steps |
具体步骤如下。
1) 联盟链成员利用本地数据集进行机器学习训练,其中机器学习算法以及学习率、迭代次数等参数为提前商定好的内容。在完成指定次数的迭代后,每位成员用CKKS公钥pk加密本地梯度。设成员Ux得到的梯度为
| $ G_{x}=\left(g_{x 1}, g_{x 2}, \cdots, g_{x n}\right) 。$ | (4) |
加密后的梯度为$\left[G_{x}\right]=E n c\left(G_{x}; p k\right)$。之后,成员Ux用本地私钥lskx对加密梯度签名,并将签名和加密梯度[Gx]发送第三方服务器。
2) 第三方服务器收到所有成员的加密梯度后先用成员的公钥验证签名,之后在梯度中加入公钥pk加密后的符合拉普拉斯分布的噪声保护梯度隐私。设拉普拉斯分布的概率密度函数为
| $ {Lap}(b)=\frac{1}{2 b} \exp \left(-\frac{|x|}{b}\right) 。$ | (5) |
成员Ux的加密噪声梯度为
| $ \left[\hat{G}_{x}\right]=\left[G_{x}\right]+\left[{Lap}(b)_{1}, {Lap}(b)_{2}, \cdots, {Lap}(b)_{n}\right] 。$ | (6) |
最后,第三方服务器公开所有成员的加密噪声梯度。
3) 联盟链领导者下载所有成员的加密噪声梯度并解密。之后,从中选出每个梯度分量的中位数构成benchmark梯度,设benchmark梯度为
| $ C={med}\left\{\hat{G}_{x}\right\}_{x=1}^{m}=\left(c_{1}, c_{2}, \cdots, c_{n}\right) \text { 。} $ | (7) |
领导者将加密后的benchmark梯度[C]以及相关消息的签名发布到联盟链。
4) 服务器从联盟链下载benchmark梯度[C],为每位成员计算[ax],
| $ \left[a_{x}\right]=\left[c_{1}\right]-\left[g_{x 1}\right]+\cdots+\left[c_{n}\right]-\left[g_{x n}\right] \text { 。} $ | (8) |
完成后向联盟链成员公开$\left\{\left[a_{x}\right]\right\}_{x=1}^{m}$。
5) 联盟链领导者下载$\left\{\left[a_{x}\right]_{x=1}^{m}\right.$ 后先对其解密,之后计算每位成员的偏离权重,即
| $ A_{x}=\frac{\frac{1}{\left|a_{x}\right|}}{\frac{1}{\left|a_{1}\right|}+\frac{1}{\left|a_{2}\right|}+\cdots+\frac{1}{\left|a_{m}\right|}}, $ | (9) |
其中:$A_{x}=\max \left\{0, A_{x}-0.001\right\}$。领导者将公钥$p k$加密后的偏离权重$\left\{\left[A_{x}\right]\right\}_{x=1}^{m}$ 以及相关消息的签名发布到联盟链。
6) 第三方服务器将生成的随机数加入成员的加密梯度中。设处理后的成员$U_{x}$ 的梯度为$\left[\widetilde{G}_{x}\right]=$ $r_{x}\left[G_{x}\right]+d_{x}$,其中$r_{x}$ 和$d_{x}$ 为生成的非零随机数。处理结束后,第三方服务器公开所有成员的梯度$\left\{\left[\widetilde{G}_{x}\right]\right\}_{x=1}^{m}$。
7) 联盟链领导者下载$\left\{\left[\widetilde{G}_{x}\right]_{x=1}^{m}\right.$,并按照如下方法计算每位成员的相关性权重$\left\{B_{x}\right\}_{x=1}^{m}$。
(a) 计算成员$U_{x}$ 的梯度与benchmark梯度的皮尔逊相关系数$\rho_{x}$,即
| $ \rho_{x}=\frac{\sum\limits_{i=1}^{n}\left(\tilde{g}_{x i}-{Avg}\left(\tilde{g}_{x}\right)\right)\left(c_{i}-{Avg}(c)\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(\tilde{g}_{x i}-{Avg}\left(\tilde{g}_{x}\right)\right)^{2}} \sqrt{\sum\limits_{i=1}^{n}\left(c_{i}-{Avg}(c)\right)^{2}}}, $ | (10) |
其中:${Avg}\left(\tilde{g}_{x}\right)$ 表示$\left\{\tilde{g}_{x 1}, \tilde{g}_{x 2}, \cdots, \tilde{g}_{x n}\right\}$ 的平均数;${Avg}(c)$ 表示$\left\{c_{1}, c_{2}, \cdots, c_{n}\right\}$ 的平均数。因为
| $ \begin{gathered} \frac{\sum\limits_{i=1}^{n}\left(\tilde{g}_{x i}-{Avg}\left(\tilde{g}_{x}\right)\right)\left(c_{i}-{Avg}(c)\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(\tilde{g}_{x i}-{Avg}\left(\tilde{g}_{x}\right)\right)^{2}} \sqrt{\sum\limits_{i=1}^{n}\left(c_{i}-{Avg}(c)\right)^{2}}}= \\ \frac{\sum\limits_{i=1}^{n}\left(r_{x} g_{x i}+d_{x}-r_{x} {Avg}\left(g_{x}\right)-d_{x}\right)\left(c_{i}-{Avg}(c)\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(r_{x} g_{x i}+d_{x}-r_{x} {Avg}\left(g_{x}\right)-d_{x}\right)^{2}} \sqrt{\sum\limits_{i=1}^{n}\left(c_{i}-{Avg}(c)\right)^{2}}}= \\ \frac{\sum\limits_{i=1}^{n}\left(g_{x i}-{Avg}\left(g_{x}\right)\right)\left(c_{i}-{Avg}(c)\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(g_{x i}-{Avg}\left(g_{x}\right)\right)^{2}} \sqrt{\sum\limits_{i=1}^{n}\left(c_{i}-{Avg}(c)\right)^{2}}}, \end{gathered} $ |
所以即使服务器用随机数隐藏了真实的成员梯度,但最终得到的$\rho_{x}$ 依然是正确的。
(b) 增大普通成员与恶意成员之间的差距,为成员$U_{x}$ 赋值[15],即
| $ \mu_{x}=\max \left\{0, \ln \left(\frac{1+\rho_{x}}{1-\rho_{x}}\right)-0.5\right\} 。$ | (11) |
(c) 计算相关性权重$\left\{B_{x}\right\}_{x=1}^{m}$,其中成员$U_{x}$ 的权重为
| $ B_{x}=\frac{\mu_{x}}{\sum\limits_{x=1}^{m} \mu_{x}} 。$ | (12) |
8) 领导者计算每位成员的总权重为
| $ Z_{x}=\frac{A_{x} B_{x}}{\sum\limits_{t=1}^{m} A_{t} B_{t}}, $ | (13) |
将这个结果加密后发布到联盟链。
9) 第三方服务器从联盟链下载数据$\left\{\left[Z_{x}\right]\right\}_{x=1}^{m}$,用无噪声的成员加密梯度与对应的权重值相乘得到$\left\{\left[Z_{x} G_{x}\right]\right\}_{x=1}^{m}$,将这个结果向联盟链公开,最后由领导者打包发布到联盟链。
在结束步骤9)后,联盟链的所有成员需要从联盟链下载最新的梯度数据,在私钥$s k$ 解密后用梯度下降法更新本地模型,即
| $ \omega^{t}=\omega^{t-1}-\eta \sum\limits_{x=1}^{m} Z_{x} G_{x} 。$ | (14) |
在本文场景中,隐私信息包括联盟链成员的模型和私有数据。针对以上信息,考虑3种窃取隐私的攻击方法:1) 第三方服务器试图通过接收到的中间信息反向推断数据拥有方的隐私信息;2) 多个联盟链成员之间合谋交换彼此获得的信息,从而推断出其他非合谋联盟链成员的隐私信息;3) 非联盟链成员通过发布在联盟链上的信息推断模型结果。下面分别讨论这3种攻击方法对框架中的隐私信息是否产生影响。
对于第1种攻击方法:在每一轮模型更新过程中,第三方服务器视图中包含的信息有全体成员的加密梯度$\left\{\left[G_{x}\right]\right\}_{x=1}^{m}$,以及加密后的benchmark梯度$[C]$、偏离权重$\left\{\left[A_{x}\right]\right\}_{x=1}^{m}$ 和成员的总权重$\left\{\left[Z_{x}\right]\right\}_{x=1}^{m}$,由于服务器没有联盟链的同态加密的私钥,所以第三方服务器无法基于以上信息推断出参与运算的数据样本和模型的具体参数。
对于第2种攻击方法:在每一轮模型更新过程中,合谋的联盟链成员的联合视图中包含的信息有合谋成员的梯度、全体成员的噪声梯度$\left\{\hat{G}_{x}\right\}_{x=1}^{m}$、参数$\left\{a_{x}\right\}_{x=1}^{m}$、带有随机数干扰的梯度$\left\{\widetilde{G}_{x}\right\}_{x=1}^{m}$ 和相关性权重$\left\{B_{x}\right\}_{x=1}^{m}$。由于第三方服务器在安全协议步骤2)和步骤6)中给不同的成员梯度加人了拉普拉斯噪声以及不同的随机数,所以合谋的成员无法根据以上信息推测出诚实参与方的具体梯度信息。
对于第3种攻击方法:非联盟链成员没有同态私钥,不仅无法得到任意一位成员的包括具体梯度数据和模型数据在内的隐私数据,而且无法判断出任意成员对模型聚合的贡献。
4 实验结果与分析硬件环境为搭载Intel i9 13900k CPU、RTX4090显卡以及64 GB内存的服务器。实验中应用的数据集为MNIST和Fashion-MNIST,MNIST和Fashion-MNIST数据集所对应的学习率分别为10-5和10-6。
4.1 投毒攻击实验本节实验测试的内容是聚合算法应对联邦学习投毒攻击的效果。投毒攻击的方法包括:1) 标签反转攻击。将选定的恶意成员的训练集中的真实标签值加1(9改为0)。2) 后门攻击。将选定的恶意成员的训练集中的标签全部改为7,并按照图 2的方式在图片中嵌入灰色长方形触发器。3) 模型投毒。每一轮本地训练结束以后,将恶意成员的每个梯度分量与随机数θ相加作为提交给第三方服务器的梯度(θ∈[-6×104,6×104])。
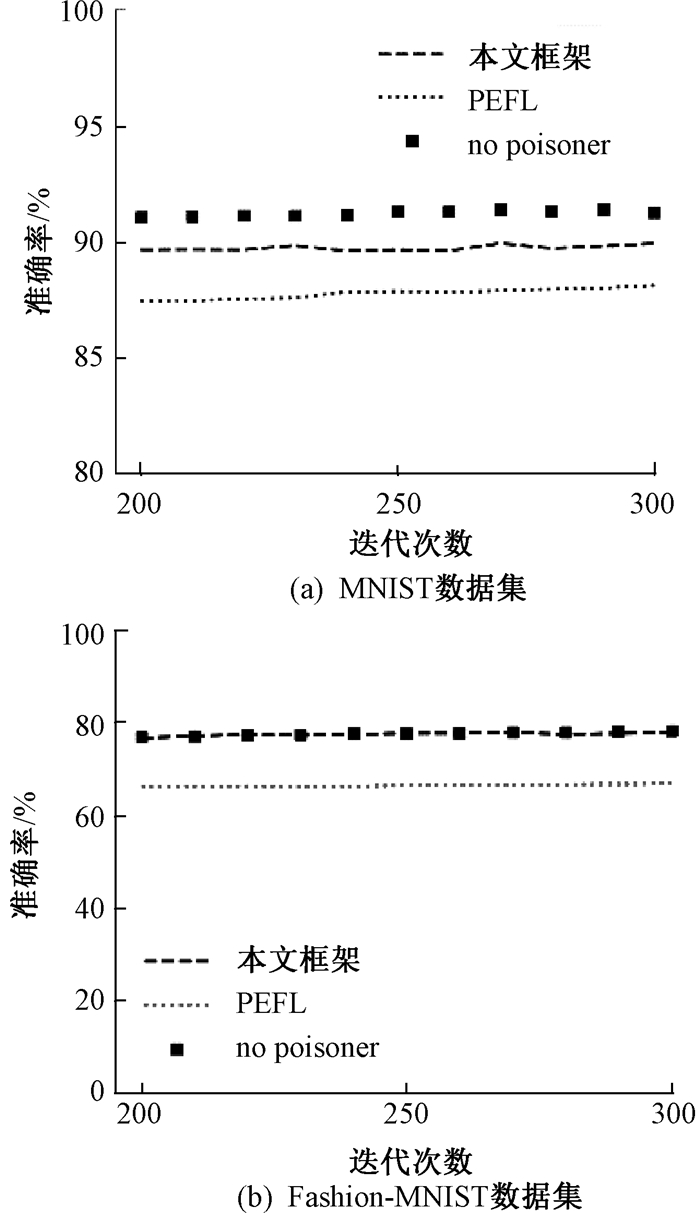
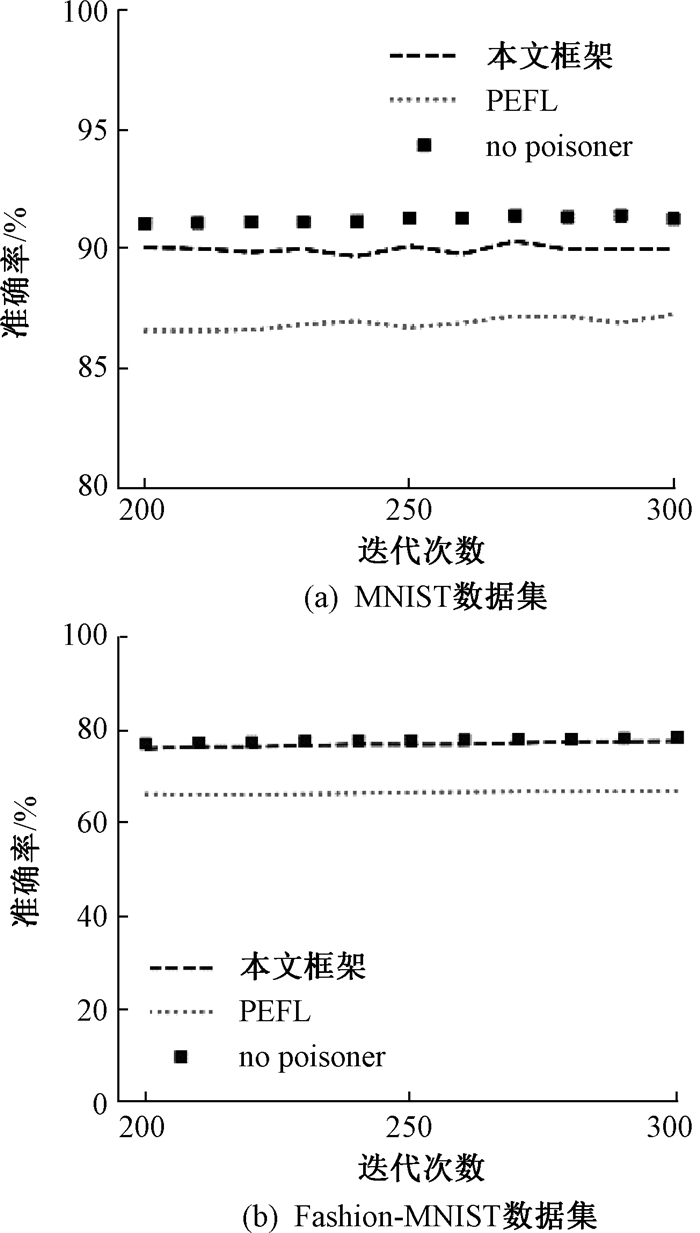
在以上相同条件下使用PEFL聚合算法[13]作为对比算法。图 4和图 5分别展示了在MNIST和Fashion-MNIST数据集上,第200次到第300次迭代过程中联邦学习框架对抗标签反转攻击和后门攻击的模型准确率,其中的恶意成员占总成员数量的40%。将恶意节点剔除后,由公式(2)所得模型被称作“no poisoner”,该模型的准确率可认为是在有恶意成员的条件下联邦学习聚合算法能够达到的准确率极限。从图 4和图 5中可以发现,在第200次迭代以后,模型准确率的变化趋于稳定,说明全局模型已经收敛,并且本文框架的准确率比PEFL算法更高,验证了所提框架的有效性。
|
图 4 在MNIST和Fashion-MNIST数据集上的标签反转攻击 Fig. 4 Label-flipping attack on MNIST and Fashion-MNIST datasets |
|
图 5 在MNIST和Fashion-MNIST数据集上的后门攻击 Fig. 5 Backdoor attack on MNIST and Fashion-MNIST datasets |
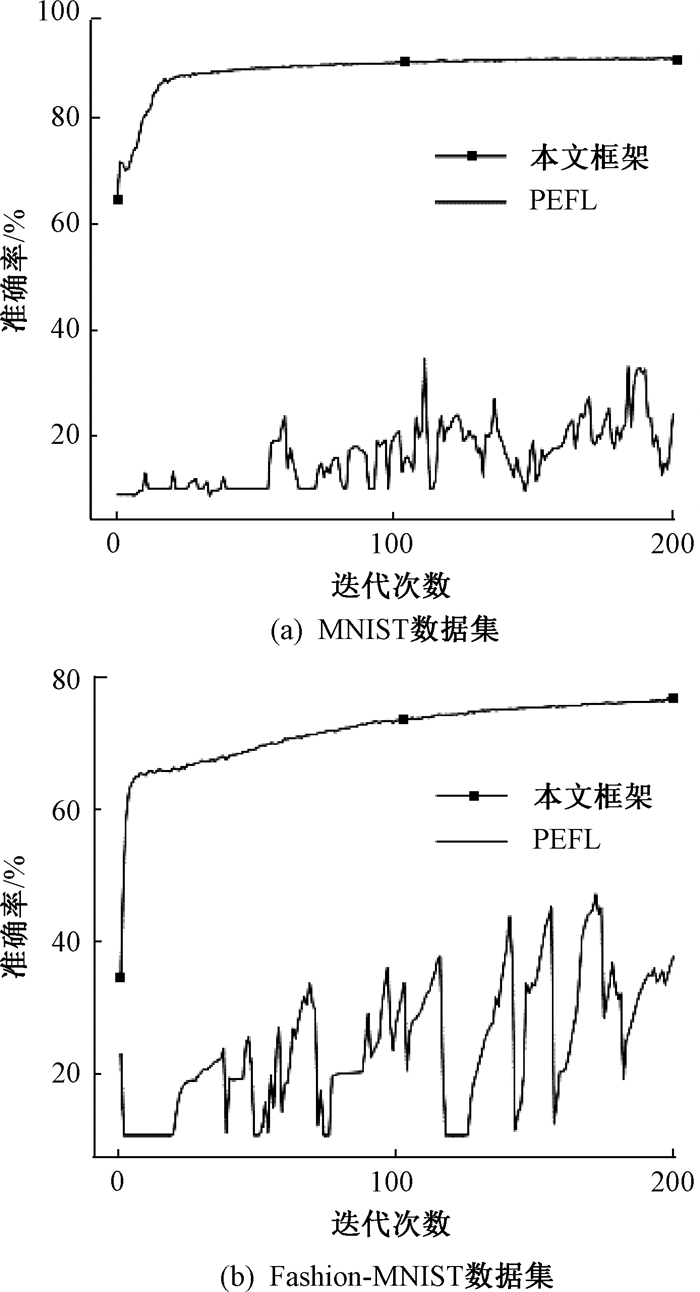
图 6展示了本文框架和PEFL算法在MNIST和Fashion-MNIST数据集上的模型投毒表现。可以看出,面对模型投毒,PEFL算法无法保证其性能的稳定性,但本文框架可以使全局模型几乎不受模型投毒的影响。这是由于本文框架不仅考虑了每位成员提交的梯度数据与benchmark梯度数据之间的相关性,同时也对成员提交的梯度数据偏离benchmark梯度数据的距离进行限制,有效减弱了模型投毒对全局模型的影响。
|
图 6 在MNIST和Fashion-MNIST数据集上的模型投毒 Fig. 6 Model poisoning on MNIST and Fashion-MNIST datasets |
文献[18]证明了用所有成员的梯度中位数可以实现联邦学习模型的收敛,2.4小节的步骤2)和步骤3)相当于在文献[18]的基础上加入噪声保护数据隐私。由于使用噪声有降低模型准确率的风险,所以本实验目的在于验证所提框架能否减小噪声对模型准确率的干扰。
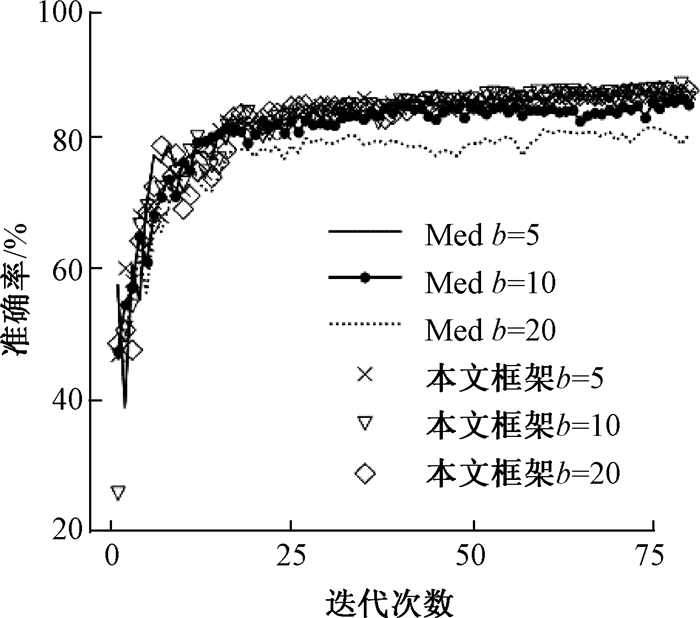
实验数据集为MNIST,联盟链成员的本地机器学习算法为逻辑回归。联盟链中一共有5位成员,其中没有恶意成员。在每一轮的训练中,每位成员从本地随机挑出100个图片数据参与训练,其余参数不变。模型更新完成后,随机取测试集中1 000个图片测试模型准确率。拉普拉斯尺度参数(b)对模型准确率的影响如图 7所示。图 7中的Med曲线表示联盟链领导者仅用benchmark梯度更新模型得到的准确率,而其余曲线则表示完整地执行本文框架实现梯度聚合及模型更新后的准确率。从图 7可以看出,如果直接使用benchmark梯度,那么梯度中的噪声尺度参数越大,全局模型的准确率就会越低。然而,相同情况下噪声尺度参数的增大对本文提出的聚合算法影响较小,这是因为在本文框架中加入拉普拉斯噪声的梯度只是为选出恶意梯度提供了一个参照,最后参与模型聚合的依然是“干净”的梯度。
|
图 7 拉普拉斯尺度参数对模型准确率的影响 Fig. 7 The impact of Laplacian scale parameters on the model accuracy |
针对当前联邦学习模型在数据隐私保护与投毒攻击防御方面的挑战,本文提出了一种基于联盟链的隐私保护联邦学习计算框架。该框架通过融入同态加密技术和拉普拉斯噪声,确保在模型训练过程中多方数据的隐私得到充分保护。同时,借助联盟链的共识机制和模型聚合算法,为各参与方动态分配梯度聚合权重,有效减轻了恶意节点对全局模型的负面影响,进而显著提升了模型的鲁棒性。在MNIST和Fashion-MNIST两个基准数据集上的实验结果表明,即便在恶意节点占比高达40%的情况下,所提框架依然能够有效防御标签反转攻击和后门攻击。
| [1] |
吴文泰, 吴应良, 林伟伟, 等. 横向联邦学习: 研究现状、系统应用与挑战[J]. 计算机学报, 2025, 48(1): 35-67. WU W T, WU Y L, LIN W W, et al. Horizontal federated learning: research status, system applications and open challenges[J]. Chinese journal of computers, 2025, 48(1): 35-67. (  0) 0) |
| [2] |
FREDRIKSON M, JHA S, RISTENPART T. Model inversion attacks that exploit confidence information and basic countermeasures[C]// Proceedings of the ACM SIGSAC Conference on Computer and Communications Security. New York: ACM Press, 2015: 1322-1333.
(  0) 0) |
| [3] |
BONAWITZ K, IVANOV V, KREUTER B, et al. Practical secure aggregation for privacy-preserving machine learning[C]//Proceedings of the ACM SIGSAC Conference on Computer and Communications Security. New York: ACM Press, 2017: 1175-1191.
(  0) 0) |
| [4] |
ZHAO K, XI W, WANG Z, et al. SMSS: secure member selection strategy in federated learning[J]. IEEE intelligent systems, 2020, 35(4): 37-49. DOI:10.1109/MIS.2020.3007207 (  0) 0) |
| [5] |
FANG H K, QIAN Q. Privacy preserving machine learning with homomorphic encryption and federated learning[J]. Future internet, 2021, 13(4): 94. DOI:10.3390/fi13040094 (  0) 0) |
| [6] |
MADI A, STAN O, MAYOUE A, et al. A secure federated learning framework using homomorphic encryption and verifiable computing[C]// Proceedings of the Reconciling Data Analytics, Automation, Privacy, and Security. Piscataway: IEEE Press, 2021: 1-8.
(  0) 0) |
| [7] |
刘振鹏, 陈杰, 王仕磊, 等. 基于聚类和压缩感知的高维数据发布算法[J]. 郑州大学学报(理学版), 2023, 55(2): 63-69. LIU Z P, CHEN J, WANG S L, et al. High dimensional data publishing algorithm based on clustering and compressed sensing[J]. Journal of Zhengzhou university (natural science edition), 2023, 55(2): 63-69. DOI:10.13705/j.issn.1671-6841.2021515 (  0) 0) |
| [8] |
BLANCHARD P, EL MHAMDI E M, GUERRAOUI R, et al. Machine learning with adversaries: Byzantine tolerant gradient descent[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM Press, 2017: 118-128.
(  0) 0) |
| [9] |
MHAMDI E M, GUERRAOUI R, ROUAULT S. The hidden vulnerability of distributed learning in Byzantium[EB/OL]. (2018-07-17)[2024-01-23]. https://doi.org/10.48550/arXiv.1802.07927.
(  0) 0) |
| [10] |
XU C, JIA Y, ZHU L H, et al. TDFL: truth discovery based Byzantine robust federated learning[J]. IEEE transactions on parallel and distributed systems, 2022, 33(12): 4835-4848. DOI:10.1109/TPDS.2022.3205714 (  0) 0) |
| [11] |
CHEN X H, JI J L, LUO C Q, et al. When machine learning meets blockchain: a decentralized, privacy-preserving and secure design[C]//IEEE International Conference on Big Data. Piscataway: IEEE Press, 2018: 1178-1187.
(  0) 0) |
| [12] |
MIAO Y B, LIU Z T, LI H W, et al. Privacy-preserving byzantine-robust federated learning via blockchain systems[J]. IEEE transactions on information forensics and security, 2022, 17: 2848-2861. DOI:10.1109/TIFS.2022.3196274 (  0) 0) |
| [13] |
LIU X Y, LI H W, XU G W, et al. Privacy-enhanced federated learning against poisoning adversaries[J]. IEEE transactions on information forensics and security, 2021, 16: 4574-4588. DOI:10.1109/TIFS.2021.3108434 (  0) 0) |
| [14] |
CHEON J H, KIM A, KIM M, et al. Homomorphic encryption for arithmetic of approximate numbers[C]//International Conference on the Theory and Application of Cryptology and Information Security. Cham: Springer International Publishing, 2017: 409-437.
(  0) 0) |
| [15] |
YIN C Y, ZENG Q K. Defending against data poisoning attack in federated learning with non-IID data[J]. IEEE transactions on computational social systems, 2024, 11(2): 2313-2325. DOI:10.1109/TCSS.2023.3296885 (  0) 0) |
| [16] |
ZHANG X L, ZHANG H L, ZHANG G M, et al. Model poisoning attack on neural network without reference data[J]. IEEE transactions on computers, 2023, 72(10): 2978-2989. DOI:10.1109/TC.2023.3280133 (  0) 0) |
| [17] |
DADDA L, MACCHETTI M, OWEN J. The design of a high speed ASIC unit for the hash function SHA-256 (384, 512)[C]//Proceedings of Design, Automation and Test in Europe Conference and Exhibition. Piscataway: IEEE Press, 2004: 70-75.
(  0) 0) |
| [18] |
CHEN Y D, SU L L, XU J M. Distributed statistical machine learning in adversarial settings: Byzantine gradient descent[J]. Proceedings of the ACM on measurement and analysis of computing systems, 2018, 1(2): 44. (  0) 0) |
 2025, Vol. 57
2025, Vol. 57

