近年来,人工智能技术应用于教育领域引起了广泛关注。认知诊断是其中的重要任务之一,旨在根据学生做题记录来评估学生对知识点的掌握情况,在教学评价和资源推荐等任务中具有重要作用[1-3]。
近年来,认知诊断的相关研究取得了丰富的成果,其方法主要分为两类。一类基于传统概率模型如IRT[4]、MIRT[5]等方法,使用习题难度、习题区分度和学生的熟练度模拟学生与习题的交互过程。确定性输入、噪声“与”门模型(DINA)[6]结合Q矩阵和学生的答题记录,对学生的认知状态进行建模。然而,上述模型依赖于人工设计的交互函数,难以捕捉学生和习题之间的复杂交互关系。另一类基于深度学习方法,该类方法基于神经网络,或建模学生和习题之间的交互关系[7]或对学生习题知识点的图结构进行表示,如CDGK[8]、RCD[9]。上述方法表明基于图结构的认知诊断方法具有良好性能。
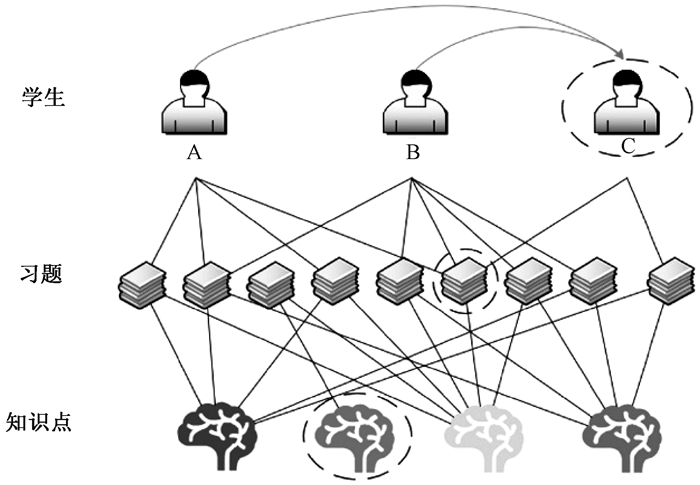
然而,上述模型的良好性能依赖于充分的数据,包括学生的做题记录、习题和知识点的关联关系等。在实际应用中,这种数据可能是不充分的,在图结构中往往呈长尾分布。例如ASSIST 2009—2010(简称ASSIST)数据集中,做题记录多于平均数的学生仅占19%,而做题记录小于40题的学生却占45%。此外,在ASSIST数据集中,关联多个知识点的题目仅占17%,而关联单知识点的题目占83%。这种学生做题记录少或知识点关联信息少的节点被称作学生尾节点或习题尾节点。显然,长尾分布中的尾节点由于具有较少信息难以进行有效建模。如图 1所示,学生A和B分别作答4个和5个习题,而学生C仅作答2个习题,可认为A和B是头节点而C是尾节点。显然,具有较少做题信息的学生C的认知状态诊断就变得困难。此外,习题和知识点中也同样存在尾节点。总之,学生、习题和知识点之间关联关系的长尾分布给已有的诊断方法带来了挑战。
|
图 1 构建学生层间相似关系的示意图 Fig. 1 Construction of the intra-layer similarity relationship |
针对数据中的长尾分布问题,本文提出了基于层内相似关系的认知诊断方法(intra-layer similarity cognitive diagnosis,ISCD)。通过构建层内相似关系,将头节点的信息传递给尾节点,缓解长尾分布现象,提高诊断精度。如图 1所示,通过构建学生A和C、B和C的相似关系(如图 1中弧线箭头),将学生A、B的做题信息传递给做题记录较少的学生C。本文主要贡献如下。
1) 针对认知诊断中学生-习题-知识点关联图中的长尾分布问题,提出通过构建层内相似关系来改善长尾,提高诊断性能。
2) 在消融实验中讨论了当学生、习题和知识点节点多种长尾分布共存时,多个层间相似关系构建的必要性。
1 相关工作本节从两个方面介绍了近两年流行的认知诊断模型:基于神经网络的认知诊断模型和基于图的认知诊断模型。
1.1 基于神经网络的认知诊断近年来,神经网络被用于改进认知诊断中手工交互函数难以模拟学生和习题之间的交互问题。DIRT基于IRT进行改进,使用神经网络来建模习题的文本以及习题和知识点之间的关系[10]。NCD利用多层神经网络对学生和习题进行建模,改进了以往人工设计的交互函数不能完全模拟学生和习题交互过程这一缺点,并经过单调性假设的验证,证明了其可解释性[7]。MGCD使用多层神经网络对一组学生的认知状态进行诊断,旨在挖掘群体对知识点的熟练度,并将群体的熟练度作为群体中个体的熟练度[11]。ECD使用层次注意网络来挖掘情境和文化对学生的影响,然后聚合学生背景信息和学生的历史认知状态生成学生的外在因素特征,以增强对学生的认知状态的诊断[12]。KSCD对每个学生的嵌入向量、习题的嵌入向量分别和知识嵌入向量相乘,得到学生知识掌握向量和习题对应知识难度向量,二者经过交互函数来预测学生答题表现 [13]。
1.2 基于图的认知诊断图神经网络的优越性能在许多领域引起了广泛关注。而认知诊断中由学生、习题、知识点间的关系构成三部图[14]。因此基于图认知的诊断方法成为研究的热点之一。
GKT-CD基于图结构,使用了一个门控GNN建模学生的学习过程,生成了学生的认知状态,提高了模型性能[15]。RCD构建了一个由三个局部图组成的层次图:学生-习题图、习题-知识点图和知识点依赖图,并用GAT学习学生、习题和知识点的嵌入表示[9],再基于多层神经网络进行优化,提高了诊断的精度。MRCD考虑学生-习题交互的差异性将学生的作答记录分为两个图进行建模,即正确作答交互图和错误作答交互图,利用图对比学习解决了图划分导致的稀疏性并增强了学生和练习的学习[16]。但二者都没有考虑同种实体之间的关系。
上述方法在图建模中多聚焦在学生、习题和知识点的层间关系,较少关注层内关系。
2 本文方法给定学生、习题和知识点集合S={s1, …, si, …, sN},E={e1, …, ei, …, eM},K={k1, …, ki, …, kT},N,M和T分别是三个集合包含的数量。假设每个学生分别选择了一些习题,而这些习题又包含某些知识点,由此构成一个三部图,将学生作答习题、习题包含知识点的关系称为层间关系,分别表示为Rse={sa↔ei sa∈S, ei∈Q},Rek={ei↔kj ei∈E, kj∈K}。实际应用中Rse和Rek的稀疏性和不均衡性,导致学生、习题和知识点呈现长尾分布,存在头节点和尾节点,从而给诊断带来挑战。本文的任务是在分布长尾条件下实现认知诊断。
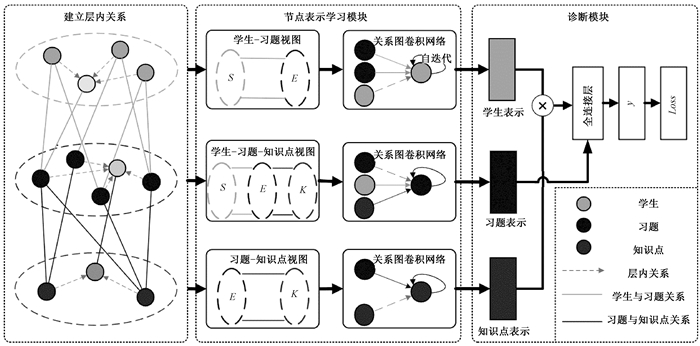
本文方法的框架分为层内相似关系构建、融合关系的节点表示和诊断模型训练三个步骤,如图 2所示。1) 层内相似关系构建主要是构建层内节点间的相似关系,从而使得头节点信息可以传递给其相似的尾节点。2) 融合关系的节点模块则是基于RGCN模型分别嵌入图中的节点,如学生、习题和知识点[17]。3) 模型训练则是在嵌入基础上训练诊断模型。
|
图 2 基于层内相似关系的认知诊断模型框架图 Fig. 2 Framework of cognitive diagnostic model based on intra-layer similarity relationships |
本节针对三部图中的长尾分布,提出了构建层内相似关系的方法来缓解尾节点的稀疏性问题。以学生节点为例,当一个学生头节点(学生做了充分的习题)和一个学生尾节点(学生仅做了少量的习题)所做的习题中有较多相同题目,则认为两个学生之间具有一定的相似性,尾节点学生有较大概率会做头节点学生所做的习题。为此,通过构建头节点和尾节点间的相似关系,使得头节点关联的习题信息可以传递给尾节点。
两个学生的作答记录相似,则这两个学生被认为存在相似关系,我们把这些相同类型节点间的关系称为层内相似关系。这里,采用简单匹配系数[18]来计算两个学生节点间的相似性,
| $ Similarity\left(s_1, s_2\right)=\frac{R_{s_1 e} \cap R_{s_2 e}}{R_{s_2 e^e} \cap \sum\limits_{i=1}^S R_{s_i^e}}, $ | (1) |
其中:Rs1e表示学生1的做题记录集合;Rs2e表示学生2的做题记录集合。
根据式(1)计算任意两个学生的相似矩阵,对相似性较大的两个学生之间构建层间相似关系,以构建学生层内的关系图。相似性阈值设置为λ=α×AVERAGE(w),其中:α为手动调整的系数;w为式(1)计算的相似系数构成的矩阵。若Similarity(sa, sb)>λ,则在这两个学生之间建立相似关系。
同理,可以基于习题间的相似性和知识点间的相似性,分别构建习题、知识点的层内相似关系。
2.2 融合关系的节点表示针对三个类型的节点,考虑学生-习题和习题-知识点间关系的不同,基于RGCN对三类节点进行嵌入。下面以学生为例进行说明。
首先基于学生-习题二部图,在随机初始化向量基础上,基于两层堆叠的RGCN,通过聚合学生层内相似节点以及学生-习题的层间关联节点进行向量迭代更新。聚合过程对邻域信息进行归一化,再求和累积,具体可表示为
| $ s_i^{(l+1)}=\sigma\left(\sum\limits_{r \in \mathbf{R}} \sum\limits_{j \in N_i^r} \frac{1}{\left|N_i^r\right|} \boldsymbol{W}_r^{(l)} n_j^{(l)}+\boldsymbol{W}_0^{(l)} s_i^{(l)}\right), $ |
其中:sil+1为神经网络隐藏层的输出;最终层的输出为学生节点si的向量表示Es;Nir表示节点i在关系r∈R下的与邻居节点的关系集合;nj(l)为si的邻居节点(包括学生和习题节点);Wr是个可训练矩阵,表示si与邻居节点的权重;W0表示整合l层自身表示的权重;σ表示激活函数,这里采用LeakyReLU。
同理,基于学生-习题-知识点视图获取习题的向量Ee,基于习题-知识点视图,获取知识点的向量Ek。
2.3 诊断模块基于学生、习题和知识点进行认知诊断建模,并基于预测结果的分类损失进行模型训练。
首先,对学生向量和知识点向量进行融合以获取学生认知状态的向量,
| $ \boldsymbol{E}_c=F C\left(\boldsymbol{E}_s, \boldsymbol{E}_k\right) \text { 。} $ |
其次,基于学生认知状态来预测学生做题结果。若学生认知状态超过习题所要求的知识点掌握情况,则预测学生答对,否则答错。因此,利用学生的认知状态和习题所要求的知识点掌握情况之间的交互作用来进行预测,
| $ y=L\left(W\left(\boldsymbol{E}_c-\boldsymbol{E}_e\right)\right), $ |
其中:Ec代表学生的认知状态;Ee代表习题所需要的知识点掌握情况。W(·)是一个池化层,对学生的认知状态和习题进行降维;L(·)是一个评分函数,用于将降维的学生认知状态和习题转化为具体的预测结果,实验中采用一层全连接层。
最后,基于Adam优化的方法来训练模型。模型的损失函数是真实得分r和预测得分y的交叉熵函数。具体来说,y是ISCD模型预测的学生S作答习题E的成绩,r是学生S在习题E上的真实成绩,因此,模型的损失表示为
| $ \text { Loss }=-\sum\limits_{i=1}^N\left(y_i \log y_i^*+\left(1-y_i\right) \log \left(1-y_i^*\right)\right) \text { 。} $ |
在三个真实世界的数据集上进行了广泛的实验,以证明本文方法在数据长尾分布下的有效性。
3.1 数据集和对比算法三个数据集的统计信息见表 1,其中“—”表示该指标在数据集中不存在。
|
|
表 1 数据集信息统计表 Tab. 1 Statistical information of three data sets |
ASSIST(ASSISTments 2009—2010 skill builder)(https://sites.google.com/site/assistmentsdata/home/2009-2010-assistment-data/skill-builder-data-2009-2010)是由ASSISTments(在线智能导师系统)收集的宣传数据集,其中包含2009—2010学年学生的回答记录以及所包含的习题与知识点之间的关系,ASSIST不提供知识点之间的关系。本文将与习题交互记录数量少于40的学生作为尾节点,余下学生作为头节点。
Mooper(massive open online practice,MOOP)是一个大型在线开放实践数据集,由国防科技大学信息系统工程重点实验室贡献[19]。Mooper来源于大规模开放在线实践,包含了2018—2019年头歌平台(https://www.educoder.net/) 用户在线实践数据,其中用户与实践项目的辅助信息以知识图谱形式组织。由于数据量大,很多习题并没有对应的知识关联,所以本文只选取了包含知识点的做题记录进行实验,并将做题数量少于10题的学生定义为尾节点。
JunYi(https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=1198)来自在线学习平台JunYi学院,该数据集收集了2012年10月—2015年1月的答题记录。每个习题只包含一个知识点。它提供了由专家标记的知识点之间的关系[20]。
将学生、习题和知识点的向量维度设置为T,T为知识点的个数。参照RCD[9]的预处理操作处理未标注数据集的知识点之间的关系。RGCN层的最大堆叠层数为2,使用Adam优化器来优化模型参数,学习率为0.001,epoch设置为100。采用5-交叉验证的方法获取实验结果,以70%的做题记录作为训练集,30%做题记录作为测试集。考虑本文使用的数据集习题是客观习题,习题的得分为0或1,分别表示不正确或正确答案。采用了ACC和AUC两种二分类模型评价指标对预测性能进行评价。
为了验证ISCD的有效性,选择两个传统模型(IRT和DINA)、两个神经网络模型(NCD和RCD)作为基线。
IRT是一种典型的连续型认知诊断模型。通过对测试问题和学生的答案进行联合建模来诊断测试参数以及学生的潜在能力[4]。
DINA是经典的认知诊断模型之一,它将学生描述为多维知识掌握向量,并从学生现有的回答记录中诊断学生的知识状态[6]。
NCD是基于神经网络的最早的CDM之一。它使用多个神经层来建模学习者和习题,并应用单调性假设来确保模型的可解释性[7]。
RCD将学习者、习题和概念表示为三个局部关系图中的节点,构建了一个多层注意网络来聚合图中节点之间的关系和图之间的关系[9]。
KSCD利用学生做题记录学习知识概念之间的关系并基于神经网络获取知识点向量的嵌入表示,再融合学生和知识点向量得到学生的认知状态[13]。
3.2 对比实验表 2对比了本文方法与多个基线在三个数据集上的效果。表中ISCD-S表示仅对学生构建层内相似关系,习题和知识点不构建层内相似关系;ISCD-E和ISCD-K分别表示仅构建习题层内关系和知识点层内关系。由表 2可得出1)~4)。
|
|
表 2 多个算法在三个数据集上的运行结果 Tab. 2 Experimental results of methods on three data sets |
1) 在基线中,基于图的RCD和ISCD效果优于其他方法,表明基于图结构学习学生、习题和知识点的策略是有效的,可以更好模拟学生-习题-知识点的复杂交互。
2) ISCD、ISCD-S、ISCD-E和ISCD-K模型的准确率在三个数据集上的表现均有提升,其中ISCD-S、ISCD-E在三个数据集上的ACC均优于上述基线模型,说明加入层内关系可以丰富图的信息,提高诊断精度。
3) ISCD-S、ISCD-E和ISCD-K在三个数据集上大部分指标优于ISCD,表明增加层内关系可以更好地捕捉学生的认知状态并提高预测准确性。
4) ISCD-S在三个数据集上的评价指标均优于ISCD-E和ISCE-K,表明增加学生层内关系比其他两个层内关系更有效。因为ISCD-S可以获取相似的学生认知状态信息,尽管ISCD-E和ISCD-K增加了习题和知识点间的关系,但该关系作为邻居通过叠加操作反映在学生状态向量中。因此,相比ISCD-E和ISCD-K,ISCD-S对于整体的诊断精度提升更明显。结果表明,ISCD系列模型在预测学生成绩方面是有效的,同时考虑学生内部和层间交互关系可以进一步提高它们的性能。
3.3 消融实验 3.3.1 建立多种层内关系的有效性为了进一步验证学生、习题和知识点层内关系同时添加的必要性,进行了诊断实验,结果见表 3。Mooper-S表示原Mooper数据集中仅学生具有长尾分布,习题和知识点不具有长尾分布;Mooper-SK表示在原Mooper数据集对增加了部分无知识点关联记录的习题,从而使得学生和知识点同时存在长尾分布;ASSIST-SE表示原ASSIST数据集中学生和习题同时具有长尾分布。ISCD-SE表示对学生、习题构建层内相似关系;ISCD-SK表示对学生、知识点构建层内相似关系;ISCD-SEK表示对学生、习题、知识点构建层内相似关系;ISCD-EK表示对习题、知识点构建层内相似关系。
|
|
表 3 加入不同关系模型诊断精度 Tab. 3 Accuracy by considering different relationships |
1) 当学生存在尾节点时,加入学生的层内关系有效。Mooper-S数据中仅学生存在长尾分布,习题和知识点不存在长尾分布。与ISCD相比,ISCD-S在Mooper-S数据集上的ACC提升了2.09%,在尾节点诊断的ACC提高了2.88%,表明针对学生尾节点,增加学生头节点和尾节点间的相似关系,能将头节点的做题信息传递给尾节点,从而提高精度。ASSIST-SE数据集学生和习题同时存在长尾,与ISCD比,ISCD-S在ASSIST-SE数据集上全体学生的ACC提升了2.75%,尾节点ACC提高了6.76%。表明当学生存在长尾分布时,增加学生节点的层内相似关系是有效的。
2) 当仅学生长尾,习题知识点不存在长尾时,仅增加习题的层内关系也能提升效果,但没有仅增加学生层内关系提升明显。在Mooper-S数据集上,与ISCD比,ISCD-E尾节点ACC提升了0.68%,而ISCD-S提升了2.88%。这是由于习题间的层内关系在RGCN过程中,通过层内关系聚合了更多的习题信息到学生节点上,从而缓解了学生尾节点的稀疏性。
3) 当仅学生长尾,习题和知识点不长尾时,增加多个层内关系提升效果不明显。ISCD-SE与ISCD-S相比,ISCD-SE比ISCD-S全体学生的ACC仅提升了0.70%,在尾节点ACC仅提升了0.29%, 提升幅度较小。表明了多个层内关系之间的叠加中具有信息重叠,难以获取明显提升。
在ASSIST-SE和在Mooper-SK数据集上分别为学生、习题长尾,学生、知识点长尾,ISCD-SE、ISCD-SK分别在这两个数据集上缓解学生和习题长尾、学生和知识点长尾的效果相较于ISCD-S在Mooper-S上缓解学生长尾的效果有着类似的优势和结论,限于篇幅,不再赘述。
3.3.2 不同建立层内关系方法及参数分析考虑潜在相似关系具有多样性,我们尝试用不同的相似度函数来建立层内相似关系,以验证诊断结果与层内关系建立方式及规模的相关性。为此,对比了简单匹配系数(SMC)、余弦相似度、Jaccard系数三个相似度计算方法随阈值变化的情况,如表 4所示。
|
|
表 4 3个层间相似性计算方法随阈值变化的诊断精度变化 Tab. 4 Comparison of diagnostic effects of different parameters and establishment methods on tail nodes |
1) Jaccard相似系数用于比较有限样本集之间的相似性与差异性[21]。Jaccard系数值越大,样本相似度越高。给定两个学生做题集合A、B,Jaccard系数定义为A与B交集的大小与A与B并集的大小的比值,定义为
| $ J(\boldsymbol{A}, \boldsymbol{B})=\frac{|\boldsymbol{A} \cap \boldsymbol{B}|}{|\boldsymbol{A} \cup \boldsymbol{B}|}=\frac{|\boldsymbol{A} \cap \boldsymbol{B}|}{|\boldsymbol{A}|+|\boldsymbol{B}|-|\boldsymbol{A} \cap \boldsymbol{B}|}, $ |
其中:A为学生1的做题集合;B为学生2的做题集合。
2) 余弦相似度把学生做题的记录作为向量,计算学生之间的余弦相似度,定义为
| $ \cos (\theta)=\frac{\boldsymbol{A} \cdot \boldsymbol{B}}{\|\boldsymbol{A}\|\|\boldsymbol{B}\|}=\frac{\sum\limits_{i=1}^n \boldsymbol{A}_i \times \boldsymbol{B}_i}{\sqrt{\sum\limits_{i=1}^n\left(\boldsymbol{A}_i\right)^2} \times \sqrt{\sum\limits_{i=1}^n\left(\boldsymbol{B}_i\right)^2}} 。$ |
根据表 4的结果可得出结论1)~2)。
1) 随着相似性阈值调整系数α增加,层内关系数量减小,尾节点的同类邻居节点数量也减小。当α在0.7时,其性能最佳。α过小时,则会增加过多的相似关系,其中可能包含了噪声;而当α过大时,则仅能增加少量相似关系。尾节点无法充分获得信息,导致诊断效果下降。
2) 三个相似性关系计算方法随阈值参数变化趋势基本一致,且余弦相似度结果最好。
4 结论本文针对学生、习题和知识点的长尾分布,提出了一种基于层内相似关系的认知诊断方法ISCD。该方法通过增加学生与学生、习题与习题、知识点与知识点之间的层内相似关系实现尾节点的信息传递,从而缓解长尾分布带来的挑战。具体而言,本文首先计算了学生、习题和知识点之间的相似性,建立层内相似关系图。然后,使用了一个关系图卷积网络来聚合头节点的信息到尾节点和不同节点上的信息,生成学生、习题和知识点的表示。最终设计一个诊断函数来预测学生的表现。未来将进一步关注更合理的层间相似关系构建方法,以及知识点长尾分布情况下,如何提升诊断性能。
| [1] |
胡学钢, 卜晨阳, 刘菲, 等. 基于学生解题分析的认知诊断研究[J]. 计算机教育, 2019(2): 50-52. HU X G, BU C Y, LIU F, et al. Research on cognitive diagnosis based on students' problem solving analysis[J]. Computer education, 2019(2): 50-52. (  0) 0) |
| [2] |
胡学钢, 刘菲, 卜晨阳. 教育大数据中认知跟踪模型研究进展[J]. 计算机研究与发展, 2020, 57(12): 2523-2546. HU X G, LIU F, BU C Y. Research advances on knowledge tracing models in educational big data[J]. Journal of computer research and development, 2020, 57(12): 2523-2546. (  0) 0) |
| [3] |
郭阳, 李全龙, 李骐. 基于学习者兴趣挖掘的个性化课程推荐方法[J]. 郑州大学学报(理学版), 2021, 53(4): 77-82. GUO Y, LI Q L, LI Q. Personalized course recommendation based on learner interest mining[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(4): 77-82. DOI:10.13705/j.issn.1671-6841.2020375 (  0) 0) |
| [4] |
EMBRETSON S E, REISE S P. Item response theory[M]. New York: Psychology Press, 2013.
(  0) 0) |
| [5] |
RECKASE M D. Multidimensional item response theory models[M]//Multidimensional Item Response Theory. New York: Springer Press, 2009: 79-112.
(  0) 0) |
| [6] |
DE LA TORRE J. DINA model and parameter estimation: a didactic[J]. Journal of educational and behavioral statistics, 2009, 34(1): 115-130. DOI:10.3102/1076998607309474 (  0) 0) |
| [7] |
WANG F, LIU Q, CHEN E H, et al. Neural cognitive diagnosis for intelligent education systems[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2020: 6153-6161.
(  0) 0) |
| [8] |
WANG X P, HUANG C D, CAI J F, et al. Using knowledge concept aggregation towards accurate cognitive diagnosis[C]//Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: ACM Press, 2021: 2010-2019.
(  0) 0) |
| [9] |
GAO W B, LIU Q, HUANG Z Y, et al. RCD: relation map driven cognitive diagnosis for intelligent education systems[C]//Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM Press, 2021: 501-510.
(  0) 0) |
| [10] |
CHENG S, LIU Q, CHEN E H, et al. DIRT: deep learning enhanced item response theory for cognitive diagnosis[C]//Proceedings of the 28th ACM International Conference on Information and Knowledge Management. New York: ACM Press, 2019: 2397-2400.
(  0) 0) |
| [11] |
HUANG J, LIU Q, WANG F, et al. Group-level cognitive diagnosis: a multi-task learning perspective[C]//IEEE International Conference on Data Mining. Piscataway: IEEE Press, 2022: 210-219.
(  0) 0) |
| [12] |
ZHOU Y Q, LIU Q, WU J Z, et al. Modeling context-aware features for cognitive diagnosis in student learning[C]//Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. New York: ACM Press, 2021: 2420-2428.
(  0) 0) |
| [13] |
MA H P, LI M W, WU L, et al. Knowledge-sensed cognitive diagnosis for intelligent education platforms[C]//Proceedings of the 31st ACM International Conference on Information & Knowledge Management. New York: ACM Press, 2022: 1451-1460.
(  0) 0) |
| [14] |
ZHANG C X, SONG D J, HUANG C, et al. Heterogeneous graph neural network[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM Press, 2019: 793-803.
(  0) 0) |
| [15] |
ZHANG J R, MO Y, CHEN C Z, et al. GKT-CD: make cognitive diagnosis model enhanced by graph-based knowledge tracing[C]//International Joint Conference on Neural Networks. Piscataway: IEEE Press, 2021: 1-8.
(  0) 0) |
| [16] |
WU K F, YANG Y H, ZHANG K, et al. Multi-relational cognitive diagnosis for intelligent education[C]//International Conference on Artificial Intelligence. Cham: Springer International Publishing, 2022: 425-437.
(  0) 0) |
| [17] |
SCHLICHTKRULL M, KIPF T N, BLOEM P, et al. Modeling relational data with graph convolutional networks[C]//European Semantic Web Conference. Cham: Springer International Publishing, 2018: 593-607.
(  0) 0) |
| [18] |
LAMBOY W F. Computing genetic similarity coefficients from RAPD data: the effects of PCR artifacts[J]. Genome research, 1994, 4(1): 31-37. DOI:10.1101/gr.4.1.31 (  0) 0) |
| [19] |
LIU K J, ZHAO X, TANG J Y, et al. Mooper: a large-scale dataset of practice-oriented online learning[M]//Knowledge Graph and Semantic Computing: Knowledge Graph Empowers New Infrastructure Construction. Berlin: Springer Press, 2021: 281-287.
(  0) 0) |
| [20] |
CHANG H S, HSU H J, CHEN K T. Modeling exercise relationships in e-learning: a unified approach[C]//Proceedings of the 8th International Conference on Educational Data Mining. Brussels: International Educational Data Mining Society. 2015: 532-535.
(  0) 0) |
| [21] |
BAG S, KUMAR S K, TIWARI M K. An efficient recommendation generation using relevant Jaccard similarity[J]. Information sciences, 2019, 483: 53-64. DOI:10.1016/j.ins.2019.01.023 (  0) 0) |
 2025, Vol. 57
2025, Vol. 57


