2. 国防科技大学 先进微处理器芯片与系统重点实验室 湖南 长沙 410073;
3. 长沙理工大学 计算机与通信工程学院 湖南 长沙 410114
2. Key Laboratory of Advanced Microprocessor Chips and Systems, National University of Defense Technology, Changsha 410073, China;
3. School of Computer and Communication Engineering, Changsha University of Science and Technology, Changsha 410114, China
随着摩尔定律的失效和晶体管尺寸的逐渐缩小,集成电路的物理设计变得越来越复杂。集成电路物理设计的复杂性带来了设计成本、效率等方面的挑战[1]。虽然静态时序分析(static timing analysis, STA)工具可以利用计算机算法和模型来模拟电路中的时序传播和延迟情况,以提供准确的时序分析结果。然而,由于先进工艺下电路的复杂性,进行准确的时序分析需要耗费大量时间。因此,如何加快时序收敛是一个关键问题。
近年来,神经网络研究在许多领域取得了显著的进展[2]。它具有强大的学习能力和模式识别能力,能够从大量数据中提取复杂的特征和关系。因此,许多学者利用神经网络对如何快速预测物理设计中的时序信息展开了研究[3]。但由于物理设计的流程复杂,现有研究并没有覆盖全面。例如,针对集成电路布线完成至确认阶段,为了加快时序收敛,减少迭代优化次数,需要快速预估单元时序;针对全定制模式,需要对新单元的时序进行快速预估。本文在循环神经网络(recurrent neural network, RNN)的基础上提出了标准单元延时预测模型(cell-delay prediction model, C-DPM),可以快速预测布线完成后的标准单元延时,从而减少迭代优化时序过程中进行STA的时间开销,加快时序收敛。主要贡献如下:(1) 创新地提出利用RNN特性来深入挖掘学习单元特性与延时之间存在的非线性映射关系,从而解决布线完成后的单元延时预测问题。(2) 在布线完成后的迭代优化时序过程中,利用C-DPM对替换或新增的标准单元进行延时预测,可以解决反复迭代的STA带来的时间开销过大的问题。(3) 在多个设计模块和不同工艺、电压、温度(process, voltage, and temperature, PVT)工艺角下进行多组实验,实验结果证明了C-DPM的普适性,C-DPM能够在多种工程条件下都取得很好的延时预测效果。
1 相关工作在集成电路物理设计中,由于电路复杂性和时序要求的限制,物理设计往往是与逻辑设计一同迭代优化的,而时序优化过程中每次迭代都需要调用STA工具来确认延时信息是否符合时序约束,而STA伴随着高昂的时间开销[4]。因此,为了加快物理设计的效率,研究人员发掘了神经网络在集成电路时序预测方面的潜力,通过快速预测物理设计中目标的时序信息,减少迭代优化过程中STA的次数。通过在大量的数据样本上进行训练,神经网络可以学习到电路结构、布局布线、工艺变异等因素与时序之间的复杂非线性关系,从中提取出隐藏的模式和特征,并进行准确的延时预测。在此基础上,研究人员利用神经网络设计了多种针对物理设计不同阶段的时序信息预测方法。例如,针对布局阶段,文献[5]提出一种基于机器学习的方法,将线延时和门延时合并进行延时预测,同时该模型不区分驱动的不同输入引脚以及上升/下降的不同时延, 统一采用最差时延进行预测。针对时钟树综合阶段,文献[6]和[7]利用统计学习和元建模方法预测时钟功率和时钟线长;文献[8]则利用人工神经网络(artificial neural network, ANN)预测瞬态时钟功耗。针对布线阶段,文献[9]提出一种基于非树形结构的构造电容和电阻图的互连线时序预测方法,具有较好的实际意义。针对确认阶段,文献[10]提出了基于机器学习的增量式时序模型来减少工具差异, 实现了确认时序工具之间的关联;文献[11]使用ANN和支持向量机进行建模,并使用混合代理模型,实现了基于非信号完整模式预测信号完整模式下的时序结果。
虽然现有的方法利用深度学习在物理设计时序信息预测领域取得了不错的进展,但由于物理设计的步骤复杂,且每个阶段对时序信息预测均有不同的需求。因此,针对某些物理设计阶段的时序信息预测仍有可以深入挖掘研究的空间。通常,在布线完成至确认阶段,对时序违例路径的优化手段是依靠工程师的经验来替换或者加入新的标准单元以实现时序收敛,而判断优化后的时序路径是否时序收敛,则需要重新消耗大量时间进行STA。迭代优化时序过程中,重复的STA带来的高昂时间开销严重降低了物理设计的效率。由于优化过程的主体对象是标准单元,因此可以通过研究对标准单元延时信息进行快速预测的方法,从而实现快速判断时序是否收敛,避免迭代过程中重复的STA。
与现有的时序信息预测方法不同,本文聚焦于布线完成后的标准单元延时预测问题,对时序信息预测进行了更细粒度的研究,利用神经网络对标准单元的延时进行快速预测。因此,本文将布线完成后的标准单元延时预测建模为回归问题。首先设计了专用算法来提取其关键特征,随后以RNN[12]为基础构建C-DPM,分别以标准单元最大、最小延时作为标签进行训练,以便可以使用训练好的C-DPM实现对标准单元最大和最小延时的快速预测,从而避免布线完成至确认阶段的迭代优化时序过程中重复进行STA,进而节省时序优化的时间开销,提高物理设计的效率。
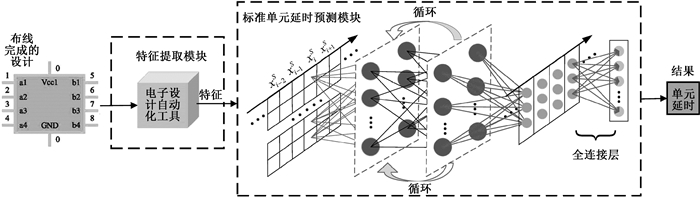
2 C-DPM的构建在集成电路物理设计中,工程师在对布线完成后的时序违例路径进行时序收敛优化时,往往会面临如何快速预估优化效果的问题。为了绕过时间开销过大的STA,实现优化效果的快速评估,通过研究该时序优化过程中标准单元的特性与其延时之间的非线性映射关系,基于RNN提出了C-DPM。C-DPM主要分为2个部分:特征提取模块和标准单元延时预测模块。其整体框架如图 1所示。
|
图 1 C-DPM整体框架 Fig. 1 The overall framework of C-DPM |
标准单元延时会受到输出负载、输入跳变等多种因素的影响,因此设计一个合理的算法对标准单元的关键特征进行提取,对于单元延迟预测的准确性至关重要。由于单元的特征除了其自身的面积、沟道长度、驱动能力等属性外,主要还包括引脚的属性,故将单元和其包含的引脚作为整体进行特征提取。在标准单元延时预测模块,以RNN模型为主干网络,由于标准单元的某些关键特征可能会在时间上延续影响对延时的预测结果,因此可以通过RNN的循环结构对标准单元的特性与延时之间的长期依赖关系进行提取。
2.1 特征提取模块特征提取模块实现了对标准单元的关键特征与延时标签的提取。具体来说,提取了标准单元的面积、沟道长度、驱动能力、阈值电压、扇出,以及标准单元输入和输出引脚(pin)的最大和最小信号的过渡(transition)、电容、电阻等17个关键属性作为标准单元的输入特征。而时序优化需要考虑最悲观和最乐观情况下延时的大小,因此同时提取了该标准单元的最大延时和最小延时,分别作为标签来训练布线完成后标准单元最大延时预测模型和最小延时预测模型。
由于对寄存器到寄存器时序路径的优化是布线阶段至确认阶段时序收敛优化过程的主体,并且在时序违例路径优化过程中往往会存在高频出现的被优化标准单元,因此以寄存器到寄存器时序违例路径为基础,抽取出时序违例路径中所含的标准单元,进而提取其特征。
不同工艺角下时序违例路径受到PVT条件的影响会出现很大的差异,因此同时对多个工艺角下时序违例路径进行提取,去除重复路径后得到时序违例路径列表。标准单元的部分关键属性以及标准单元的延时也会受到PVT条件的影响而产生变化,以时序路径列表为基础,通过同时在不同工艺角下提取标准单元的关键特征和延时标签来研究不同工艺角对模型产生的影响。
考虑不同标准单元所包含的输入、输出引脚的数量可能不同,从而导致特征的长度不一致,因此取标准单元所含的所有输入引脚中最大和最小的过渡、电容、电阻作为关键属性。输出引脚同理。具体的提取算法如下:首先利用电子设计自动化(EDA)工具提取设计中所有工艺角下不重复的时序违例路径,其次对每条时序违例路径提取出路径中的所有标准单元,针对每个标准单元提取出单元的属性以及单元的所有输入、输出引脚,再针对输入、输出引脚提取出对应所需的引脚的属性。最后,将所有的属性作为一个集合得到单元特征列表。
2.2 标准单元延时预测模块为了挖掘布线完成后的标准单元特性与其延时之间存在的非线性映射关系,在利用特征提取算法提取到单元特性后,将其作为RNN模型的输入,并以延时作为标签信息,自动学习它们之间存在的隐藏关系,输出经由RNN计算后得到的延时特征。由于RNN在处理计算时,计算序列中的当前输出与前面的输出是相关的,神经网络会对前面的信息进行记忆并应用于当前输出的计算之中,而标准单元的关键特征可能会在时间上延续影响对延时的预测结果。因此,可以对关键特征之间的关联进行提取,进而加强对延时特性的映射关系。
具体来说,将提取出的标准单元特征作为RNN模型的输入。假设xt∈RX表示t时刻的输入,X为输入的维度。在正向传播过程中,xti表示t时刻某个样本的第i维输入,也就是隐藏层第i个神经元的输入;ht∈RH表示t时刻隐藏层第i个神经元的输出,H为隐藏层的维度。
t时刻隐藏层第j个神经元的输入为
| $ \boldsymbol{c}_t^{H_j}=\sum\limits_{i=1}^X \boldsymbol{x}_t^i \boldsymbol{W}_{i j}+\sum\limits_{s=1}^H \boldsymbol{h}_{t-1}^s \boldsymbol{U}_{s j}+\boldsymbol{b}_j^H, $ | (1) |
其中:Wij表示输入层到隐藏层的权重矩阵;Usj表示隐藏层上一次的输出值作为本次输入时的权重矩阵;bjH为隐藏层第j个神经元的偏置。
t时刻隐藏层第j个神经元的输出为
| $ \boldsymbol{h}_t^j=\tanh \left(\boldsymbol{c}_t^{H_j}\right) 。$ | (2) |
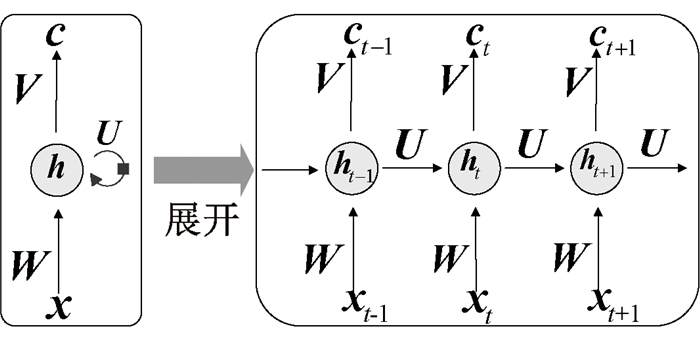
隐藏层向量的计算过程如图 2所示。
|
图 2 隐藏层向量的计算过程 Fig. 2 The calculation process of hidden layer vector |
t时刻输出层第k个神经元的输入为
| $ \boldsymbol{c}_t^{Y_k}=\sum\limits_{j=1}^H \boldsymbol{h}_t^j \boldsymbol{V}_{j k}+\boldsymbol{b}_k^Y, $ | (3) |
其中:Vjk表示隐藏层到输出层的权重矩阵;bkY为输出层第k个神经元的偏置。
t时刻输出层第k个神经元的输出为
| $ \boldsymbol{y}_t^{Y_k}=\tanh \left(\boldsymbol{c}_t^{Y_k}\right)。$ | (4) |
在经过RNN模型的计算之后可以得到最终的延时特征矩阵Yfinal,随后在RNN模型之后设计了一个全连接层,其公式为
| $ \boldsymbol{Z}=\operatorname{ReLU}\left(dropout\left(\boldsymbol{V} \boldsymbol{Y}_{\text {final }}\right)\right), $ | (5) |
其中:Z为最终的延时预测结果;ReLU为激活函数;dropout为随机失活;V为可学习的权重矩阵。
3 实验部分 3.1 实验数据与参数设置为了充分验证所提模型的有效性,选取了在亚30 nm工艺下的6个设计模块,包括4个公开的模块Ethnet、Leon3mp、B19、Netcard以及2个工业设计模块Design1和Design2。同时,为了验证不同PVT条件对模型的影响,选取了5个PVT工艺角: 工艺角1(125 ℃,rcworst,0.99 V)、工艺角2(125 ℃,rcbest,0.99 V)、工艺角3(0 ℃, cworst,0.99 V)、工艺角4 (0 ℃,rcworst,0.99 V)、工艺角5 (0 ℃,rcbest,0.99 V)。对6个设计模块均采用商用EDA工具完成布局布线与时序分析后,在5个PVT工艺角下利用特征提取算法对时序违例路径上的标准单元特征进行提取。6个设计模块中标准单元数量如表 1所示。
|
|
表 1 6个设计模块中标准单元数量 Tab. 1 The number of standard cell in six design modules |
在表 2中,总单元数量表示该电路中总的标准单元数量,抽取单元数量表示以寄存器到寄存器时序违例路径为基础,抽取出时序违例路径中所含的标准单元总数。由于每个设计模块在布线阶段结束后的时序收敛程度不同,可能会出现某个设计模块的总单元数量较多,但时序违例路径上的标准单元数量却较少的情况。本文主要针对寄存器到寄存器的时序违例路径上时序收敛优化过程的加速问题,因此选择时序违例路径上的标准单元作为实验样本,并不用所有标准单元作为数据集。同时,将EDA工具完成布线阶段后STA的标准单元最大、最小延时分别作为标签。由于集成电路工程实践场景与常规的神经网络训练场景不同,在该场景下预测的目标范围是固定的,因此并没有采取神经网络训练过程中对数据集划分的一般做法,而是在80%的样本上进行训练,在整个数据集上进行预测。
|
|
表 2 不同设计模块在5个工艺角下的平均绝对误差 Tab. 2 The mean absolute errors of different design modules within 5 corners |
为了对比RNN模型的优越性,将主干网络换为卷积神经网络(convolutional neural network,CNN)模型(C-DPMCNN)进行了对比实验。为公平起见,对CNN模型与RNN模型统一了主干网络参数量和超参数设置。具体来说,在实验中将学习率设置为1×10-7,训练批次大小为128,随机失活率为0.3,Adam优化器的L2正则化权重为1×10-7,隐藏层网络的输入维度为32,激活函数采用ReLU。
3.2 度量标准为了更好地对模型的预测效果进行评价,采用了平均绝对误差(MAE)和决定系数(R2)。MAE表示真实值与预测值之间的绝对差值,可以准确反映实际标准单元延时预测误差的大小。R2是指总离差平方和中回归平方和所占的比重。R2越接近1,单元特征对延时预测值的解释程度越高,表明延时预测回归的拟合效果越好,观察点在回归直线附近越密集。MAE和R2的具体计算公式分别为
| $ MAE(y, \hat{y})=\frac{1}{N} \sum\limits_{i=1}^N\left|y_i-\hat{y}_i\right|, $ | (6) |
| $ R^2(y, \hat{y})=1-\frac{\sum\limits_{i=1}^N\left(y_i-\hat{y}_i\right)^2}{\sum\limits_{i=1}^N\left(y_i-\frac{1}{N} \sum\limits_{i=1}^N y_i\right)^2}, $ | (7) |
其中:y为真实值;
在5个PVT工艺角下,分别对C-DPM和C-DPMCNN进行了训练,随后对布线完成后标准单元最大延时预测和最小延时预测进行了实验。表 2和表 3分别给出了C-DPM和C-DPMCNN中不同设计模块在5个工艺角下的平均绝对误差和决定系数结果。
|
|
表 3 不同设计模块在5个工艺角下的决定系数 Tab. 3 The determination coefficients of different design modules within 5 corners |
从表 2和表 3可以看出,C-DPM的最大延时预测的平均绝对误差为0.519 ps~1.310 ps,最小延时预测的平均绝对误差为0.380 ps~1.016 ps。在小设计模块(Ethnet)中,C-DPM实验效果最差,这可能是由于训练数据不足,很难提取到单元特征与延时之间的映射关系。总的来说,当模块的单元数量级越大时,C-DPM对于最大延时和最小延时的预测效果越接近于1 ps/0.7 ps的误差,同时R2指标也越接近于1,表明模型的拟合效果越好。此外,从表 2和表 3还可以看出,PVT工艺角对C-DPM的影响并不明显,也就是说,C-DPM可以很好地适应各种工艺角条件,对不同PVT工艺角条件下的标准单元延时均能进行准确预测。
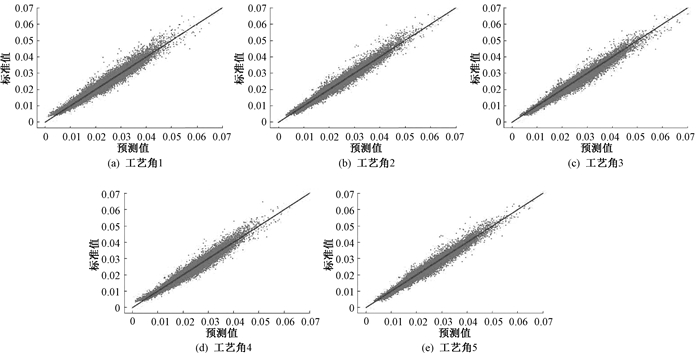
值得注意的是,对比C-DPM和C-DPMCNN的实验结果可以发现,在不同设计模块和PVT工艺角条件下,C-DPM的表现均优于C-DPMCNN,这表明RNN能更好地提取出某些关键特征在时间上的延续影响,从而提取出更有效的延时特征,使得模型效果更佳。图 3为5个工艺角条件下C-DPM对Design1的最大延时预测回归拟合。可以看出,在5个工艺角条件下,C-DPM对Design1的建立时间延时预测点十分紧凑地拟合在回归直线附近。但随着延时的增大,预测点也随之分散,表明C-DPM在延时值较低时能达到更好的预测效果。这可能是由于较大的延时值过于稀疏,底层分布特征漂移,从而使得模型在大延时值预测时效果略显不足。
|
图 3 5个工艺角条件下C-DPM对Design1的最大延时预测回归拟合 Fig. 3 The maximum delay predictive regression fitting of C-DPM on Design1 within 5 corners |
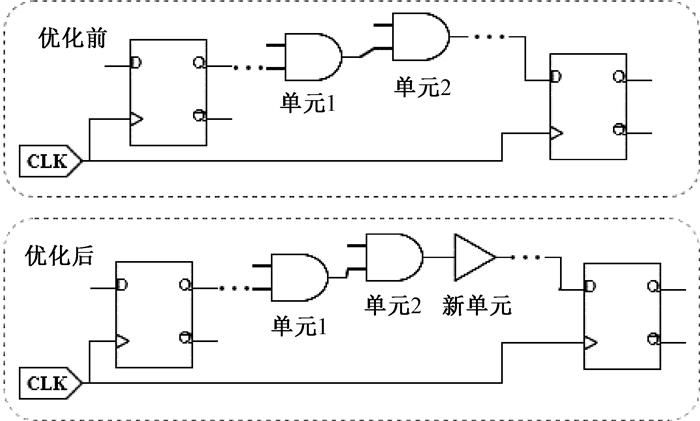
在实际物理设计工程中,工程师完成布线后,为了实现时序收敛,可以依靠其经验对时序违例路径进行标准单元替换或加入新的标准单元,随后可以利用C-DPM对优化后的时序路径是否符合时序约束进行预估。选取了Design2中保持时间违例的一条路径进行了演示。电路优化前后示意图如图 4所示。按照经验在该条时序违例路径上替换了2个单元,同时插入了1个新单元,以此提高路径延时,满足保持时间约束。为了保证在最乐观的情况下仍能满足约束,对单元的最小延迟进行了预测,电路优化前后单元最小延时预测结果如表 4所示。可以看出,C-DPM对于单元延时的预测误差能保持在一个非常小的范围内。通过对单元延时的准确预估,工程师可以快速判断该次优化操作是否有效,从而加速整个时序收敛优化过程,减少迭代优化过程中冗余的STA操作带来的时间开销。
|
图 4 电路优化前后示意图 Fig. 4 Schematic diagram before and after circuit optimization |
|
|
表 4 电路优化前后单元最小延时预测结果 Tab. 4 Prediction results of minimum cell delay before and after circuit optimization |
本文聚焦于布线完成至确认阶段对时序收敛优化过程加速的问题,提出了C-DPM来对标准单元延时进行快速预测。实验结果表明,C-DPM能适应不同PVT工艺角条件下的标准单元时序预测,对单元数量级大的物理设计模块有着更稳定的预测效果。与现有方法相比,在实际物理设计工程应用中,C-DPM的标准单元延时预测结果能够指导工程师快速预估布线完成后时序优化操作是否有效,减少迭代优化过程中进行STA的次数,缩小时间开销,加快物理设计速度。未来,将继续深入研究提升电路延时预测准确率以及预测速度的方法。
| [1] |
GARGINI P. The international technology roadmap for semiconductors[EB/OL]. (2022-01-02)[2023-05-16]. http://www.itrs2.net/itrs-reports.html.
(  0) 0) |
| [2] |
ABIODUN O I, JANTAN A, OMOLARA A E, et al. State-of-the-art in artificial neural network applications: a survey[J]. Heliyon, 2018, 4(11): 1-41. (  0) 0) |
| [3] |
贺旭, 王耀, 傅智勇, 等. 敏捷设计中基于机器学习的静态时序分析方法综述[J]. 计算机辅助设计与图形学学报, 2023, 35(4): 640-652. HE X, WANG Y, FU Z Y, et al. A survey on machine learning-based technology for static timing analysis in agile design[J]. Journal of computer-aided design & computer graphics, 2023, 35(4): 640-652. (  0) 0) |
| [4] |
LEE Y, WATERMAN A, COOK H, et al. An agile approach to building RISC-V microprocessors[J]. IEEE micro, 2016, 36(2): 8-20. DOI:10.1109/MM.2016.11 (  0) 0) |
| [5] |
BARBOZA E C, SHUKLA N, CHEN Y, et al. Machine learning-based pre-routing timing prediction with reduced pessimism[C]//Proceedings of the 56th Annual Design Automation Conference. New York: ACM Press, 2019: 1-6.
(  0) 0) |
| [6] |
KAHNG A B, LIN B, NATH S. Enhanced metamodeling techniques for high-dimensional IC design estimation problems[C]//Design, Automation & Test in Europe Conference & Exhibition. Piscataway: IEEE Press, 2013: 1861-1866.
(  0) 0) |
| [7] |
KAHNG A B, LIN B, NATH S. High-dimensional metamodeling for prediction of clock tree synthesis outcomes[C]//ACM/IEEE International Workshop on System Level Interconnect Prediction. New York: ACM Press, 2013: 1-7.
(  0) 0) |
| [8] |
KWON Y, JUNG J, HAN I, et al. Transient clock power estimation of pre-CTS netlist[C]//IEEE International Symposium on Circuits and Systems. Piscataway: IEEE Press, 2018: 1-4.
(  0) 0) |
| [9] |
CHENG H H, JIANG I H R, OU O. Fast and accurate wire timing estimation on tree and non-tree net structures[C]//57th ACM/IEEE Design Automation Conference. New York: ACM Press, 2020: 1-6.
(  0) 0) |
| [10] |
HAN S S, KAHNG A B, NATH S, et al. A deep learning methodology to proliferate golden signoff timing[C]//Design, Automation & Test in Europe Conference & Exhibition. Piscataway: IEEE Press, 2014: 1-6.
(  0) 0) |
| [11] |
KAHNG A B, LUO M L, NATH S. SI for free: machine learning of interconnect coupling delay and transition effects[C]//ACM/IEEE International Workshop on System Level Interconnect Prediction. New York: ACM Press, 2015: 1-8.
(  0) 0) |
| [12] |
LAI S W, XU L H, LIU K, et al. Recurrent convolutional neural networks for text classification[C]//Proceedings of the 29th AAAI Conference on Artificial Intelligence. New York: ACM Press, 2015: 2267-2273.
(  0) 0) |
 2025, Vol. 57
2025, Vol. 57


