2. 嵩山实验室 河南 郑州 450046;
3. 郑州市区块链与数据智能重点实验室 河南 郑州 450002;
4. 河南省科技创新促进中心 河南 郑州 450007
2. Songshan Laboratory, Zhengzhou 450046, China;
3. Zhengzhou Key Laboratory of Blockchain and Data Intelligence, Zhengzhou 450002, China;
4. Henan Science and Technology Innovation Promotion Center, Zhengzhou 450007, China
毁伤预测是通过对战场上的目标和武器系统进行分析和评估,预测在战斗行动中可能对敌方目标造成的损害和影响程度,从而辅助作战决策。传统的毁伤预测方式一般需要进行大量的公式计算,根据各种参数进行仿真得出结果,速度相对较慢。现有的毁伤预测模型中超参数优化方法通常未在训练时间成本、收敛速度和模型精度方面进行整体权衡, 导致一定的局限性。随着深度学习的发展,神经网络的应用为毁伤预测问题的解决提供了新的思路。其中,超参数的设置是重要的一环,会直接影响模型训练的效果。通过人工参与调整超参数的方法在超参数较多时需要进行大量的实验和反复修改,成本较高。因此,利用各种智能算法进行超参数寻优逐渐成为主流[1-2]。
近年来,群体智能算法[3]在参数调优方面应用广泛,如蚁群算法[4]、粒子群优化算法[5-6]、灰狼优化算法[7]等在参数优化问题中都有着不错的表现,也在人工智能领域得到了较好的应用。此外,在输入数据的预处理上,主成分分析法(principal components analysis,PCA)等统计学方法也起到了至关重要的作用,经过预处理的数据再参与模型的训练[8],可以进一步缩短训练时间,并有可能提高结果的准确率。
本文针对毁伤预测中神经网络超参数的搜索和优化问题,提出一种基于特征选择结合群体智能(feature selection and swarm intelligence algorithm,FS-SIA)的超参数优化方法,利用多种特征排序方法进行输入特征的重要性排序,并选取公共的特征偏序子集参与模型训练,有效地降低了弱相关度的特征对网络的噪声,提高了毁伤预测网络训练的效率。此外,利用多种群体智能算法进行超参数的搜索和优化,并基于对特征集表现最优的超参数开展大规模数据训练,在一定基础程度上再次提升了毁伤预测网络的收敛速度和模型精度,从而获得更好的战场决策效果。
1 相关知识 1.1 特征选择特征选择[9]又称特征子集选择,是指从已有的N个特征中选择M个特征(M < N)来达到特定指标最优化。特征选择的一般过程包括:1) 产生过程。即搜索特征子集的过程,为评价函数提供特征子集。2) 评价函数。是评价一个特征子集好坏的准则。3) 停止准则。一般是一个条件函数,达到条件函数就可以停止搜索。4) 验证过程。在验证数据集上验证选出来的特征子集的有效性。
常见的特征选择有前向特征选择与后向特征消除两种。前向特征选择是针对目标进行迭代,从而选择性能最佳的特征,然后选择另一个与第一个特征相结合后性能最佳的特征。后向特征消除则是选择所有特征并且在每次迭代中删除最不重要的特征。
1.2 群体智能算法不同的群体智能算法思路类似,可以归结为以下步骤:1) 初始化。即按照一定规则对待求解问题,随机初始化一组值,代入实际问题中计算出适应度。适应度是评判一组解好坏的标准。2) 评估。通过适应度函数来评估每个个体或粒子的适应度,即目标函数的值。3) 选择。根据每个个体的适应度,选择出优秀的个体。在某些算法中,采用概率性选择策略,即适应度高的个体被选中的概率大。4) 更新。根据不同的群体智能算法的更新规则,迭代更新所求的值直到满足终止条件。5) 终止条件。设定合适的终止条件,如达到最大迭代次数、达到目标函数值的阈值等。6) 输出结果。输出最优或近似最优解作为最终结果。
2 基于FS-SIA的超参数优化方法基于FS-SIA的超参数优化方法的主要过程如下。
第1步 针对数据集,利用多种特征排序方法进行输入特征的重要性排序,并按照不同方法排序后取其公共偏序子集,得到筛选后的特征集合,即
| $ F s=\left\{F s_1, F s_2, \cdots, F s_m\right\},$ | (1) |
| $ \left\{\begin{aligned} \operatorname{ \mathit Sort}_1({ data })= & <f e_{11}, f e_{12}, \cdots, f e_{1 n}>, f e_{1 i} \in F e, \\ \operatorname{ \mathit Sort}_2({ data })= & <f e_{21}, f e_{22}, \cdots, f e_{2 n}>, f e_{2 j} \in F e, \\ & \vdots \\ \operatorname{ \mathit Sort}_m ({ data }) & =<f e_{m 1}, f e_{m 2}, \cdots, f e_{m n}>, f e_{m k} \in F e, \end{aligned}\right. $ | (2) |
式(1)中,Fs是特征选择方法集合,通过每种特征选择方法进行特征排序。式(2)中,Sortm( )代表第m种特征选择方法进行特征排序,得到的有序特征集合均属于原特征集合Fe中的元素且数量相同。
第2步 将第1步得到的结果按照顺序取偏序子集进行数据筛选,即
| $ \mathit \Omega={subset}\left({ Sort }_1, { Sort }_2, \cdots, { Sort }_m\right),$ | (3) |
式中:subset()为取偏序子集操作,即取多种排序序列中最大的相同子序列集合。此步骤为取偏序子集的过程,经过多种特征选择排序方法得到的特征序列经过subset()函数后得到筛选特征序列Ω。
第3步 对第2步得到的结果进行数据集的划分,划分数据集可以按照顺序进行划分,也可以通过随机选取进行划分。划分过程为
| $ \left\{\begin{array}{l} { dataset }_{\mathrm{train}}={splitdt}(\mathit\Omega, \alpha, \text { dataset }), \\ { dataset }_{\mathrm{test}}={splitdt}(\mathit\Omega, \beta, \text { dataset }), \end{array}\right. $ | (4) |
式中:splitdt( )为划分数据集函数;α, β分别为划分训练集和测试集的比例。
第4步 采用群体智能算法初始化粒子位置(超参数),进行神经网络训练,即
| $ \boldsymbol { position }= { initial }\left(\boldsymbol{v a l}_{\text {min }}, \boldsymbol{v a l}_{\max }\right), $ | (5) |
| $ ({ fitness }, { loss })=N N( \boldsymbol { position }), $ | (6) |
式中:initial()为初始化参数函数,传入最大值和最小值即可完成位置初始化,其中最大值和最小值的选取根据需要调试的超参数来确定;position,val min,val max均为n维向量,n为待优化的超参数个数;NN代表神经网络训练过程;fitness和loss分别为适应度和损失,这里的fitness是自定义的适应度函数,在本文的实验中使用的是准确率,即毁伤预测正确的个数占比。
第5步 更新并记录每代的最佳位置和适应度,即
| $ { position }_{i+1}=U_{\mathrm{SIA}}\left({ position }_i\right)。$ | (7) |
经过神经网络训练后,可以得到每一个位置的fitness和loss值(也可将loss值作为适应度,则可简化为一个输出量)。记录每一代的最佳适应度,若未达到终止条件,则继续进行神经网络训练,直至达到终止条件。
第6步 对比各个群体智能优化算法,选取最优的超参数进行网络训练,直至达到终止条件,输出结果。
3 基于FS-SIA的毁伤预测模型基于FS-SIA的毁伤预测模型采用双隐藏层网络进行训练,模型如图 1所示。对于FS-SIA方法中的群体智能算法,选取量子粒子群算法(QPSO)[10-12]、粒子群算法(PSO)、人工蜂群算法(ABC)[13]、蚁群算法(ACO)和退火算法(SA)[14]来优化超参数。在FS-SIA方法中,特征选择过程可以选择多个算法,本文选取皮尔逊相关系数法和随机森林法。
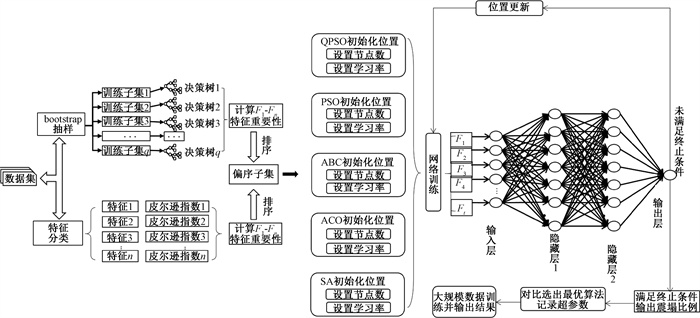
|
图 1 基于FS-SIA的毁伤预测模型 Fig. 1 Damage prediction model based on FS-SIA |
皮尔逊相关系数是用来度量两个变量之间相关性的指标,范围介于-1到1之间。
对于一组样本Xij, Yi,将Xij简写为Xi,其皮尔逊相关系数为
| $ r^j=\frac{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sqrt{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)^2} \sqrt{\sum\limits_{i=1}^n\left(Y_i-\bar{Y}\right)^2}}。$ | (8) |
随机森林法是利用多棵决策树对样本进行训练与预测的一种分类器组合方法,其集成了多个模型,提高了预测的准确率。随机森林模型不仅可以用来进行分类或回归,还可以通过特征重要性指标帮助选择最重要的特征来解释模型的预测结果。特征重要性指标是基于特征对模型预测的贡献程度进行排序,通常采用Gini重要性来评判特征的相关性。Gini重要性中Gini系数是常用的判断标准,特征Xj的Gini系数为
| $ G I_a=1-\sum\limits_{k=1}^K p_{a k}^2, $ | (9) |
式中:K表示类别个数;pak表示节点a中类别k所占的比例。对于特征Xj在节点a分支前后Gini系数变化量可表示为
| $ F I_{j a}^{ \mathrm{Gini}}=G I_a-G I_1-G I_{\mathrm{r}}, $ | (10) |
式中:GIl和GIr分别表示左、右新节点的Gini系数。若特征Xj在决策树b中出现的节点在集合H中,则Xj在第d棵树中的重要性可表示为
| $ F I_{d j}^{\mathrm{Gini}}=\sum\limits_{a \in H} F I_{j a}^{\mathrm{Gini}}。$ | (11) |
假设有c棵树,Xj在c棵树中的重要性之和可表示为
| $ F I_j^{\mathrm{Gini}}=\sum\limits_{d=1}^n F I_{d j}^{\mathrm{Gini}}。$ | (12) |
进行归一化后可表示为
| $ F I_j^{\mathrm{Gini}}=\frac{F I_j^{\mathrm{Gini}}}{\sum\limits_{d=1}^Z F I_d^{\mathrm{Gini}}}, $ | (13) |
式中:Z代表特征个数。归一化后的结果即为FIGinij,排序后可得出特征重要性的递减序列。对于FS-SIA方法中的群体智能算法,选取了QPSO、PSO、ABC、ACO和SA算法。以QPSO为例,该算法对粒子移动进行了优化,与之前移动的方向没有任何关系,增加了粒子位置的随机性。其更新步骤如下。
步骤1 平均粒子的历史最好位置Mbest的计算公式为
| $ M^{\text {best }}=\frac{1}{M} \sum\limits_{i=1}^M P_i^{\text {best }}, $ | (14) |
式中:M表示粒子个数;Pibest表示第i个粒子的历史最好位置。
步骤2 对每个粒子进行更新,
| $ P_i=\mathit\Phi P_i^{\text {best }}+(1-\mathit\Phi) G^{\text {best }}, $ | (15) |
| $ X_{i+1}=P_i \pm \gamma\left|M^{\text {best }}-X_i\right| \ln \left(\frac{1}{u}\right), $ | (16) |
式中:Pi表示第i个粒子更新位置的中间量;Φ和u为服从(0, 1)的均匀分布;Gbest表示全局最优的粒子位置;Xi表示第i个粒子的位置;γ为控制系数,一般不大于1。式(16)中取“+”和“-”的概率均为0.5。
在图 1中,数据集经过皮尔逊指数和随机森林特征重要性的计算后进行排序,取两种排序的偏序子集作为筛选后的特征集合。数据筛选后进行群体智能算法初始化,即初始化隐藏层节点数和学习率。经过神经网络训练后,判断是否达到终止条件。若未达到终止条件则进行更新,更新后继续训练;若达到终止条件,则输出震塌比例(O1)、准确率和loss值。可根据问题的背景设置loss阈值或准确率阈值等其他终止条件,本文设置为达到群体智能算法的最大迭代次数即满足终止条件。
4 实验与分析 4.1 数据集的选取与处理选取了某型动能弹打击某坚固地面目标的数据,其数据特征分为弹药参数、目标参数、弹目交会参数三类, 共有12个特征,记为F1, F2, …, F12。输出为毁伤结果即建筑物震塌比例,其范围为[0, 1],数据量为10 000条,其中20%作为测试集。分别计算出F1, F2, …, F12的皮尔逊相关系数和随机森林特征重要性指数,其结果如表 1所示。
|
|
表 1 特征重要性结果 Tab. 1 Feature importance results |
由表 1可以看出,偏序子集为前5个特征组成的集合。为了测试不同组合所对应的效果,选取以下4组特征集进行对比实验。
第1组:Fi(i=1, 5, 2, 12, 3);
第2组:Fi(i=1, 5, 2, 12, 3,4, 8);
第3组:Fi(i=1, 5, 2, 12, 3,4, 8, 6, 10, 11);
第4组:Fi(i=1,…,12)。
其中,第1组是按照两种特征选择方法取偏序子集得到的序列,其余组是在第1组的基础上分别添加了若干个额外特征。上述分组是按照随机森林中的特征排序进行编排,目的是对比选取出最佳的特征组合,达到噪声最小且训练速度最快。
4.2 训练过程对经过特征选取后的数据集进行归一化处理,然后进行训练。实验采用双隐藏层的BP神经网络,待优化的参数为两个隐藏层节点数和学习率,分别记为Node1、Node2和Lr,且满足:
| $ \begin{aligned} & \max \left\{{Node}_1\right\}=\max \left\{{ Node }_2\right\}=30, \\ & \min \left\{{ Node }_1\right\}=\min \left\{{ Node }_2\right\}=1,\\ & L r_{\text {min }}=0.0001, L r_{\max }=0.05。\end{aligned} $ | (17) |
结合式(5)和式(17)对第1批粒子进行初始化,按以往经验选择其最大值、最小值。实验评价指标选取均方损失(loss)与准确率, 其中loss可表示为
| $ { loss }=\frac{1}{h} \sum\limits_{i=1}^h \frac{1}{2}\left(y_i-f\left(x_i\right)\right)^2, $ | (18) |
式中:h为测试集的个数;yi为第i个样本的真实值;f(xi)为预测值。回归任务中没有准确率的评价指标,本文采用了分类思想来统计准确率。yi的取值范围为0~1,选取误差率[15]不超过2%,不同情况下的正确条件如表 2所示。
|
|
表 2 不同情况下的正确条件 Tab. 2 Correct conditions in different cases |
算法参数设置如下:QPSO算法选取20个粒子,更新30次,控制系数为0.6;PSO算法选取20个粒子,更新30次,c1 =c2=2, r1=0.7,r2=0.5, w取0和1之间的随机数;ABC算法选取蜂群个数为20,代数为30;ACO算法选取代数为30,蚁群数量为20;SA算法选取初始温度为100,结束温度为4.3,降温系数为0.9,实例个数为20。
4.3 结果与分析为了验证特征选择的必要性,按照4.1节中的4组特征集进行了对比实验,对输入端的特征个数进行区分来选取最佳的特征组合。对比实验的输出均为震塌比例,范围为[0, 1]。采用双隐藏层的神经网络,隐藏层节点数均为2 L(L为输入特征个数),学习率为0.005,优化器均为Adam,迭代次数分别为5 000和10 000,误差率不超过2%。特征选择前后结果对比如表 3所示。
|
|
表 3 特征选择前后结果对比 Tab. 3 Comparison of results before and after feature selection |
从表 3可以看出,对于未进行特征选择的数据集,迭代5 000次和10 000次的准确率和loss值均不理想。这是由于在处理前的数据中有部分输入对结果所产生的噪声较严重,且训练时间过长。相较于未进行特征选择的数据集,特征选择后的数据集所表现出来的准确率和loss值均有不同程度的提升。需要说明的是,由于精度的数量级在10-4和10-3之间,loss值需要在10-8~10-7数量级才会有较为可观的准确率(如loss值为0.000 3只对应2.5%的准确率,在本实验中为正常现象)。在表 3中,第1组的表现是最好的,在5 000次迭代时达到59.80%的准确率,在10 000次迭代时达到95.15%的准确率,loss值均达到了10-8的数量级,说明了取皮尔逊指数和随机森林排序后的偏序子集为最佳集合。第2组稍有逊色, 迭代5 000次和10 000次的准确率分别为33.40%和35.60%。第3组的结果更不理想,和未经过筛选的结果相差不大。经过对比实验,验证了特征选择的必要性。特征选择后,需要利用群体智能算法优化神经网络,选用了QPSO、PSO、ACO、ABC和SA算法对神经网络进行优化。对每种算法均设置30代更新过程,以准确率作为评价标准,记录每一代更新后的g_best,其变化趋势如图 2所示。对不同算法的运行时间和g_best的收敛值进行了统计,结果如表 4所示。
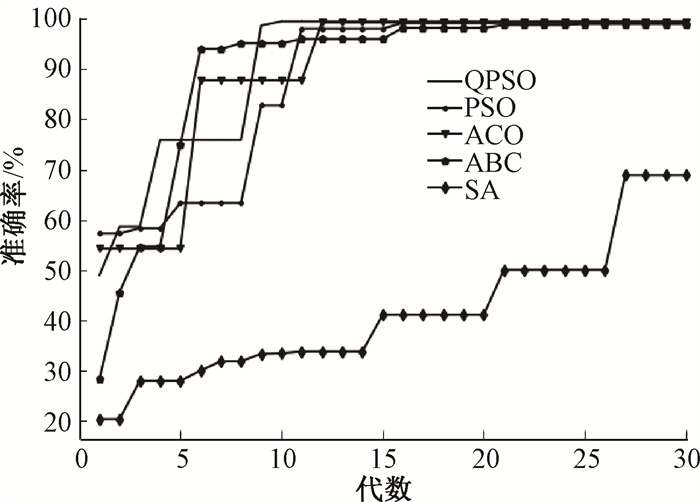
|
图 2 g_best变化趋势 Fig. 2 The trend of g_best |
|
|
表 4 不同算法的运行时间和收敛值结果 Tab. 4 The running time and convergence value results of different algorithms |
从图 2可以看出,QPSO算法在收敛速度上优势较为明显,除了SA算法,其他算法均在30代以内达到收敛的状态。由表 4可知,QPSO、PSO、ACO、ABC算法的最终准确率均能在2%误差内达到99%以上,相较于表 3中的特征选择对比实验,其准确率有进一步提升。不同的群体智能算法虽然达到峰值的代数不同,但准确率在整体上是有提高的趋势。在运行时间上,PSO算法的运行时间较短,约400 s,而QPSO算法的运行时间在500 s左右,相差较小。综合来看,QPSO算法在所选取的数据集上展现出的效果最佳。
对经过QPSO优化后网络训练的每一代全局最优loss值进行了统计,其变化趋势如图 3所示。
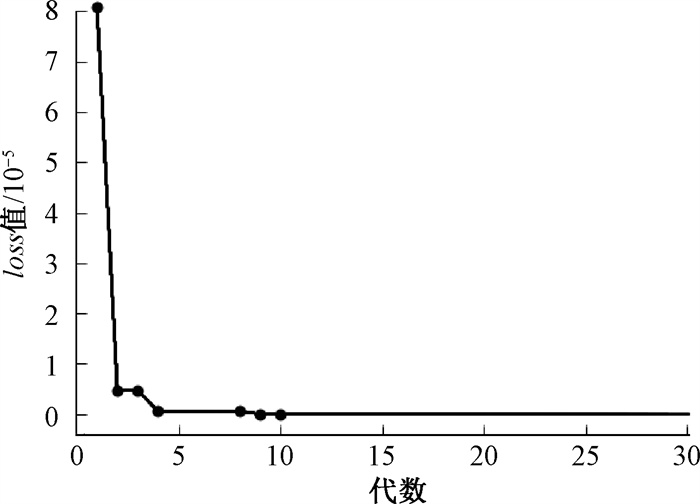
|
图 3 loss值变化趋势 Fig. 3 The trend of loss values |
经过数据统计,loss值在第1代为8.07×10-5,经过优化后,在第30代收敛到4.37×10-9。相对表 3中经过特征选择后的loss值更小,准确率更高。
4.4 贝叶斯超参数调优实验对比目前在超参数调优领域中, 贝叶斯超参数调优方法[16]在时间成本和精度上均较为优秀。本文也进行了贝叶斯超参数调优实验,迭代次数同为30,其结果如图 4所示。可以看出,在相同迭代次数的情况下,利用贝叶斯方法进行超参数调优,准确率最高为88.95%,达到最高值的代数为11,且并未看到准确率达到收敛状态。因此,对于所使用的数据集,贝叶斯超参数优化方法能达到的最高准确率不如FS-SIA方法。
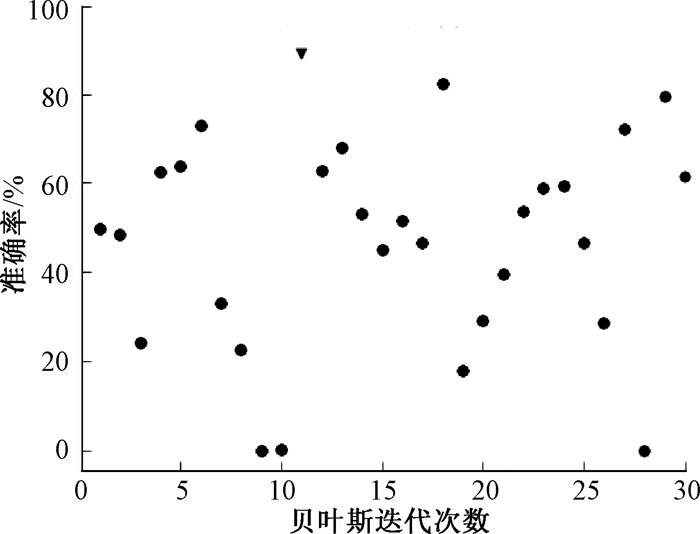
|
图 4 贝叶斯超参数调优结果 Fig. 4 Bayesian hyperparameter tuning result |
本文针对超参数调优在毁伤预测方向进行了实验,提出了基于FS-SIA的毁伤预测模型。从实验结果可知,特征选择有效地降低了相关度较弱的特征对网络产生的噪声,提高了网络训练的效率并加快了收敛速度。同时,借助群体智能算法优化超参数,进一步提升了准确率和降低了损失。采用某型动能弹打击某坚固地面目标形成的数据集,所提毁伤预测模型在实验中展现出较为优秀的预测效果。若针对其他领域进行数值预测,该模型还需要根据领域特点开展进一步的研究。
| [1] |
李发陵, 彭娟. 基于大数据的复杂超参数优化组合方法仿真[J]. 计算机仿真, 2022, 39(7): 332-336. LI F L, PENG J. Simulation of complex hyperparameter optimization combination method based on big data[J]. Computer simulation, 2022, 39(7): 332-336. DOI:10.3969/j.issn.1006-9348.2022.07.064 (  0) 0) |
| [2] |
ROSTAMIAN A, HEIDARYAN E, OSTADHASSAN M. Evaluation of different machine learning frameworks to predict CNL-FDC-PEF logs via hyperparameters optimization and feature selection[J]. Journal of petroleum science and engineering, 2022, 208: 109463. (  0) 0) |
| [3] |
高岳林, 杨钦文, 王晓峰, 等. 新型群体智能优化算法综述[J]. 郑州大学学报(工学版), 2022, 43(3): 21-30. GAO Y L, YANG Q W, WANG X F, et al. Overview of new swarm intelligent optimization algorithms[J]. Journal of Zhengzhou university (engineering science), 2022, 43(3): 21-30. (  0) 0) |
| [4] |
LEITE W L, SHEN Z C, MARCOULIDES K, et al. Using ant colony optimization for sensitivity analysis in structural equation modeling[J]. Structural equation modeling, 2022, 29(1): 47-56. DOI:10.1080/10705511.2021.1881786 (  0) 0) |
| [5] |
SHAMI T M, EL-SALEH A A, ALSWAITTI M, et al. Particle swarm optimization: a comprehensive survey[J]. IEEE access, 2022, 10: 10031-10061. (  0) 0) |
| [6] |
LI Z L, ZHU W M, ZHU B, et al. Thermal error modeling of electric spindle based on particle swarm optimization-SVM neural network[J]. The international journal of advanced manufacturing technology, 2022, 121(11): 7215-7227. (  0) 0) |
| [7] |
鲍伟, 任超. 基于GWO-BP神经网络的电池SOC预测方法研究[J]. 计算机应用与软件, 2022, 39(9): 65-71. BAO W, REN C. Research on prediction method of battery SOC based on GWO-BP network[J]. Computer applications and software, 2022, 39(9): 65-71. (  0) 0) |
| [8] |
HU T, LI X S, YOU J A. The weighted fusion prediction algorithm of acoustic interval optimized by PCA-PSO-BP and MLRM[J]. Journal of physics: conference series, 2022, 2258(1): 012004. (  0) 0) |
| [9] |
李郅琴, 杜建强, 聂斌, 等. 特征选择方法综述[J]. 计算机工程与应用, 2019, 55(24): 10-19. LI Z Q, DU J Q, NIE B, et al. Summary of feature selection methods[J]. Computer engineering and applications, 2019, 55(24): 10-19. (  0) 0) |
| [10] |
刘佳敏, 吴庆宪, 王玉惠, 等. 基于量子粒子群优化的无人机攻防博弈决策[J]. 火力与指挥控制, 2022, 47(9): 73-78. LIU J M, WU Q X, WANG Y H, et al. UAV game decision based on quantum particle swarm optimization[J]. Fire control & command control, 2022, 47(9): 73-78. (  0) 0) |
| [11] |
冯华丽, 刘渊, 陈冬. QPSO算法优化BP网络的网络流量预测[J]. 计算机工程与应用, 2012, 48(3): 102-104. FENG H L, LIU Y, CHEN D. Network traffic prediction based on BPNN optimized by QPSO algorithm[J]. Computer engineering and applications, 2012, 48(3): 102-104. (  0) 0) |
| [12] |
ZHU X T, XU B. Power short-term load forecasting based on QPSO-SVM[J]. Advanced materials research, 2012, 591/592/593: 1311-1314. (  0) 0) |
| [13] |
ZHOU B H, ZHAO Z. An adaptive artificial bee colony algorithm enhanced by deep Q-learning for milk-run vehicle scheduling problem based on supply hub[J]. Knowledge-based systems, 2023, 264: 110367. (  0) 0) |
| [14] |
KASSAYMEH S, AL-LAHAM M, AL-BETAR M A, et al. Backpropagation neural network optimization and software defect estimation modelling using a hybrid salp swarm optimizer-based simulated annealing algorithm[J]. Knowledge-based systems, 2022, 244: 108511. (  0) 0) |
| [15] |
李慧轩. 数理统计在计量检测中的应用[J]. 统计理论与实践, 2021(6): 58-61. LI H X. Application of mathematical statistics in metrological detection[J]. Statistical theory and practice, 2021(6): 58-61. (  0) 0) |
| [16] |
李亚茹, 张宇来, 王佳晨. 面向超参数估计的贝叶斯优化方法综述[J]. 计算机科学, 2022, 49(S1): 86-92. LI Y R, ZHANG Y L, WANG J C. Survey on Bayesian optimization methods for hyper-parameter tuning[J]. Computer science, 2022, 49(S1): 86-92. (  0) 0) |
 2025, Vol. 57
2025, Vol. 57


