2. 郑州大学 智能传感研究院 河南 郑州 450002;
3. 汉威科技集团股份有限公司 河南 郑州 450001;
4. 郑州大学 力学与安全工程学院 河南 郑州 450001
2. Institute of Intelligent Sensing, Zhengzhou University, Zhengzhou 450002, China;
3. Hanwei Electronics Group Corporation, Zhengzhou 450001, China;
4. School of Mechanics and Safety Engineering, Zhengzhou University, Zhengzhou 450001, China
半导体制造系统中最复杂的环节就是晶圆制造。由于晶圆制造系统漫长的重入性制造过程和其内部多种复杂资源,使得该系统成为现代大规模复杂生产系统的典型代表[1-2]。为了解决晶圆制造系统中的调度问题,文献[3]提出一种可重入的混合流水车间(re-entrant hybrid flow shop, RHFS),它具有重入的本质特征,可以有效地解决复杂的车间调度问题。RHFS的可重入性使其比其他的流水车间和作业车间问题更加复杂,且RHFS已被证明为NP-hard问题[4]。RHFS技术可以提供更高的性能和可靠性[5],已经被广泛应用于各种工业设备,尤其在半导体晶圆、印刷电路板和薄膜晶体管液晶显示器中应用更加广泛。
近年来,国内外已有很多学者对RHFS问题进行研究,并取得一定的成果。文献[6]给出一种采用拉格朗日松弛的方法,用于简化RHFS问题的加权实现周期。文献[7] < 给出一种迭代Pareto贪心启发式算法,用于求解双目标RHFS问题,以达到最小化最大完工时间和总延误的目的。文献[8-9]利用一种新的NEH-IGA方法来解决RHFS问题,可以有效地缩短最大完成时限和总加权完成时间。文献[10]设计了一种改进的多目标灰狼优化算法,可以缩短RHFS问题的最终完工时间和总拖期时间。文献[11]提出一种基于Minkowski距离交叉算子的局部搜索的Pareto遗传算法,解决了具有串行阶段的RHFS调度问题。
多元宇宙算法(multi-verse optimizer, MVO)是由Mirjalili等[12]设计的一种基于物理机理的新型智能优化算法,它是通过模拟在白洞、黑洞以及虫洞中转移宇宙中的物质而进行设计的。MVO算法拥有自组织和自调整的能力,可以根据调度问题的实际情况来自适应,在可接受的时间内求得高质量的解,近年来被逐渐应用于生产调度问题。文献[13]使用MVO算法来解决流水车间的劣化效应问题。文献[14]针对云计算任务调度完成时间的单目标问题, 提出了基于改进的MVO算法的云任务调度策略。文献[15]建立了考虑运行成本和负荷波动的多目标社区综合能源系统优化调度模型,并提出一种基于Pareto理论的多目标MVO算法求解模型。文献[16]设计了改进的MVO算法来解决热轧混合流水车间的多目标调度问题。文献[17]提出一种耦合横纵向个体更新策略的改进MVO算法来提高其全局探索和局部开采能力。文献[3]使用具有学习效应的MVO算法来解决RHFS调度问题,但是算法容易陷入局部收敛,在大规模的生产调度问题中表现不佳。基于此,本文在该算法的基础上提出一种改进的离散MVO算法,通过对MVO算法的向最优宇宙移动策略、宇宙更新策略等进行改进,使算法更适应大规模问题的求解。
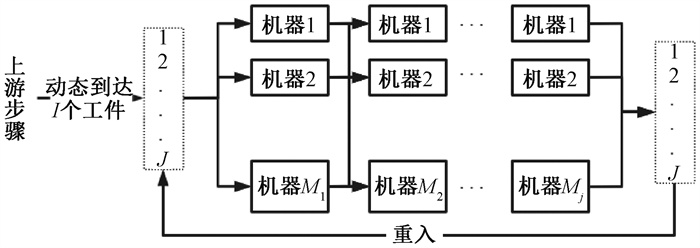
1 问题模型RHFS问题模型可以描述为:一共有I个待加工工件,每个工件需要经过J个步骤加工处理并重复L次,每个加工步骤有Mj台机器,在确定某些参数的情况下,需要为工件确定正确的加工顺序,并为工件的每个加工步骤选择合适的加工机器,以实现最小化最大完成时间。RHFS调度示意图如图 1所示。
|
图 1 RHFS调度示意图 Fig. 1 RHFS scheduling diagram |
在RHFS问题模型中,工件之间的优先级没有限制,一旦加工步骤开始就不能中断。为了更好地模拟重复加工的过程,用重入层来描述重复加工,并将重入层设置为L-1层,将Ri设定为工件i在第1层第1个步骤加工之前的释放时间,以便更准确地模拟出加工过程,从而提高加工效率。
1.1 符号定义I为工件集合,I={i i=1, 2, …, I},其中:i为工件编号;I为工件总数。J为加工步骤集合,J ={j=1, 2, …, J},其中:j为步骤编号;J为步骤总数。L为重入层次集合,L={l=1, 2, …, L},其中:l为重入层次编号;L为总的加工次数。K为时间集合,K ={k=1, 2, …, K},其中:k为某时刻;K为计划考虑的时间范围。Mj为第j个加工步骤的机器总数;Pi, j, l为第i个工件在第l层第j个步骤所需的加工时间;Tl, j, j+1为加工过程中前后两个步骤之间工件所需的传输时间,当l≠1时,Tl, 0, 1>0, 表示从l-1层的最后一个加工步骤到第l层的第1个加工步骤所需的传输时间;Xijlk表示k时刻第i个工件正在第l层的第j个加工步骤上进行加工;Cijl表示第i个工件在第l层的第j个阶段的完工时间;Cmax为最大完工时间。
1.2 数学模型目标函数为
| $ \begin{equation} \min C_{\max } \circ \end{equation} $ | (1) |
机器能力约束为
| $ \begin{equation} {\sum\limits^I_{i=1}} \sum\limits_{l=1}^L X_{i j l k} \leqslant M_j, \forall i \in \bar{I}, k \in \bar{K}_{\circ} \end{equation} $ | (2) |
工件加工时间约束为
| $ \begin{equation} \sum\limits_{k=1}^K X_{i j l k}=P_{i, j, l}, \forall i \in \bar{I}, j \in \bar{J}, l \in \bar{L}_{\circ} \end{equation} $ | (3) |
加工步骤优先级约束为
| $ \begin{equation} C_{i, j-1, l}+P_{i, j, l}+T_{l, j-1, j} \leqslant C_{i, j, l}, \forall i \in \bar{I}, j \in \bar{J}, l \in \bar{L}_{\circ} \end{equation} $ | (4) |
工件动态到达约束为
| $ \begin{equation} C_{i, j-1, l}-P_{i, 1, l}+1 \geqslant R_i, \forall i \in \bar{I}, j \in \bar{J}, l \in \bar{L}_{\circ} \end{equation} $ | (5) |
式(1)表明,本文目标是尽可能地缩小最大完工时间,为了实现这一目标,设定了一系列约束条件;式(2)表示k时刻第j个步骤的机器个数永远比在l层第j个加工步骤进行加工的工件总个数多或者相等;式(3)表示Pi, j, l为第i个工件在第j个步骤的加工时长;式(4)表示只有在某层的前一阶段或前一层的最后阶段加工完成,并运输到该层的下一阶段或该层的第1阶段后才能开始加工;式(5)表示任何一个工件必须在它到达第1层的第1个步骤之后才能开始加工。
Cijl的取值范围为
| $ \begin{equation} C_{i j l} \geqslant 0, \forall i \in \bar{I}, \forall j \in \bar{J}, l \in \bar{L}_{\circ} \end{equation} $ | (6) |
Xijlk的取值范围为
| $ \begin{equation} X_{i j j k} \in\{0,1\}, \forall i \in \bar{I}, j \in \bar{J}, l \in \bar{L}, k \in \bar{K}_{\circ} \end{equation} $ | (7) |
MVO算法可以分为两个阶段:探测和开采。在第1阶段,利用白洞和黑洞的概念来探索搜索空间;而在第2阶段,则利用虫洞来开采搜索空间,以获取更多的信息。在RHFS调度问题中,一个调度问题的可行解作为一个宇宙,每一个工件作为宇宙中的一个物质,定义每个宇宙适应度值为其膨胀率,适应度函数定义为可行解最大完工时间的倒数。初始化种群公式为
| $ \boldsymbol{U}=\left[\begin{array}{cccc} x_1^1 & x_1^2 & \cdots & x_1^d \\ x_2^1 & x_2^2 & \cdots & x_2^d \\ \vdots & \vdots & & \vdots \\ x_n^1 & x_n^2 & \cdots & x_n^d \end{array}\right], $ | (8) |
其中:d为搜索空间的维度;n为多元宇宙的个数;xij表示第i个宇宙的第j个分量。在每次迭代中,MVO算法会按照宇宙的膨胀率对宇宙种群进行排序,并采用轮盘赌法的方式从中选出一个宇宙作为白洞,与另一个作为黑洞的宇宙进行物质交换,具体公式为
| $ \begin{equation} x_i^j=\left\{\begin{array}{l} x_k^j, r 1<N I\left(U_i\right), \\ x_i^j, r 1 \geqslant N I\left(U_i\right), \end{array}\right. \end{equation} $ | (9) |
式中:r1为[0, 1]间的随机数;NI(Ui)为第i个宇宙的归一化膨胀率;xkj为通过轮盘赌法选出的第k个宇宙的第j个分量。宇宙中的物质可以通过白洞/黑洞转移策略从一个高膨胀率的宇宙(白洞)转移到一个低膨胀率的宇宙(黑洞),从而实现转移。因此,宇宙的总体膨胀率将在多次迭代中持续增加。为了改进宇宙自身膨胀率,MVO算法会通过虫洞将当前最优宇宙的物质传递到当前宇宙,具体公式为
| $ \begin{equation} x_i^j=\left\{\begin{array}{c} X_j+T D R \times\left(\left(u b_j-l b_j\right) \times r 4+l b_j\right), \\ r 3<0.5, r 2<W E P, \\ X_j-T D R \times\left(\left(u b_j-l b_j\right) \times r 4+l b_j\right), \\ r 3 \geqslant 0.5, r 2<W E P, \\ x_i^j, r 2 \geqslant W E P, \end{array}\right. \end{equation} $ | (10) |
式中:r2, r3, r4均为[0, 1]范围内的随机数;Xj为当前最优宇宙的第j个分量;ubj和lbj分别代表xij的上界和下界;WEP为虫洞存在的概率,
| $ \begin{equation} T D R=1-\frac{l^{1 / p}}{L^{1 / p}}, \end{equation} $ | (11) |
式中:WEPmin代表WEP的最小值,设定为0.2;WEPmax代表WEP的最大值,设定为1;l为当前迭代次数。
TDR为物体向当前最优宇宙移动的步长,其更新公式为
| $ $ | (12) |
式中:p定义了随迭代次数改变的探测速度。p值越高,局部探测速度越快,用时越短。为了开发准确性,设定p=6。
WEP在迭代过程中线性增大,以在后期进行更多的虫洞交换,从而加快收敛速度。TDR在迭代过程中非线性减小,减小速率先快后慢。因为在迭代前期选出的最优种群适应度不高,所以开采时要通过一个较大的移动距离来保持宇宙种群的多样性,避免宇宙种群过早同化。而在迭代后期,最优宇宙具有较高的适应度,需要通过减小移动距离来加快收敛速度。
2.2 改进的离散MVO算法标准的MVO算法只适合在连续的解空间中寻找较优解问题。基于RHFS调度问题的解空间是离散的,参考文献[18]中方法将MVO算法离散化,并在此基础上进行改进,使其更适合于RHFS调度问题。
在原始MVO算法中,主要是通过判断随机数r1和膨胀率Ui的大小来决定白洞/黑洞转移策略。如果r1小于Ui,则用Uk的第j个分量代替Ui的第j个分量,否则不发生改变。但是,RHFS调度问题中每个工件的编号唯一,如果使用原来的转移策略会使更新之后的解不合法。对于RHFS调度问题,在Ui的第j个分量需要更新时,通过交换Uk的第j个位置的分量和Ui的第j个位置的分量,以保证解的合法性。
在标准的MVO算法中,通过在迭代过程中和最优宇宙进行物质交换,使宇宙种群不断地向最优宇宙靠近,从而增加算法收敛速度,提高宇宙种群整体的膨胀率。而在原始MVO算法中,这种向最优宇宙移动策略通过将最优宇宙相应位置分量直接加/减一个实数距离来实现。对应于车间调度问题,相当于直接把最优解的第j个加工工件基于工件编号进行移动,由于在车间调度问题中编号只是用于识别工件,连续编号之间的工件并没有关联性,所以这种更新策略并不适应于车间调度问题。相比于工件编号,工件所在的加工次序对调度结果的影响更大。同时,基于车间调度的离散性,对向最优宇宙移动策略进行了相应的改进,以确保MVO算法更适用于车间调度问题。改进后的向最优宇宙移动策略公式为
| $ \begin{equation} \left\{\begin{array}{l} x_i^{j+\left\lceil T D R\left(\left(u b_j-l b_j\right) r 4+l b_j\right)\right\rceil}=x_j, r 3<0.5, r 2<W E P, \\ x_i^{j-\left\lceil T D R\left(\left(u b_j-l b_j\right) r 4+l b_j\right)\right\rceil}=x_j, r 3 \geqslant 0.5, r 2<W E P, \\ x_i^j=x_i^j, r 2 \geqslant W E P, \end{array}\right. \end{equation} $ | (13) |
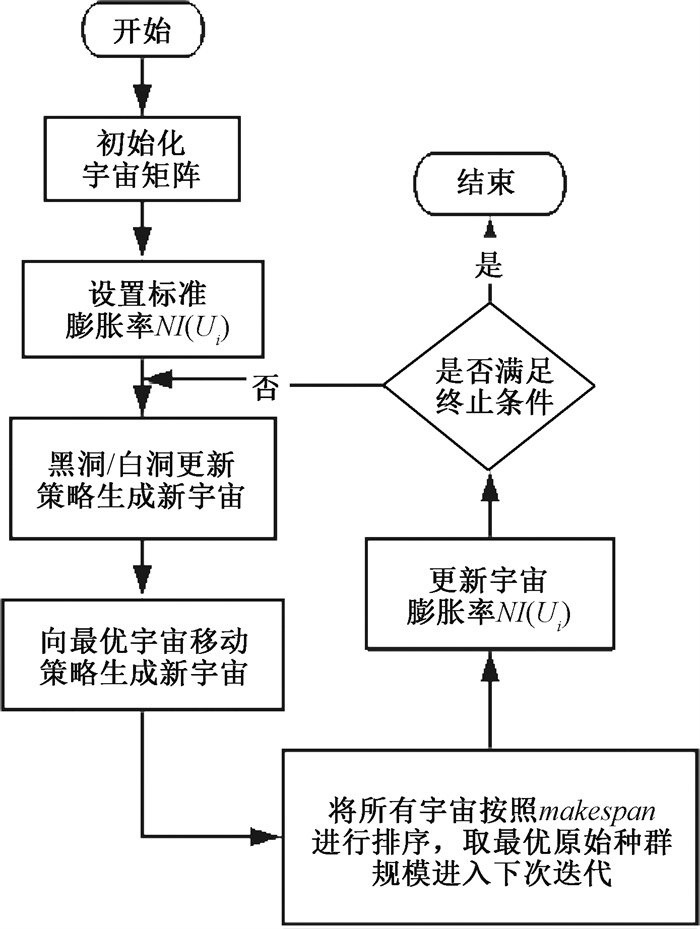
如果Ui的分量值更新后超出最大工件编号,则将其置为最大工件编号。在标准的MVO算法进行交换更新时都是对宇宙本身直接进行交换,但是并不能确定当前的更新是否使当前宇宙更优,这会导致在迭代的过程中,宇宙种群不是一直向使最大完工时间变小的方向进行,寻优效率不高。本文借鉴遗传算法(genetic algorithm, GA)优胜劣汰的思想,在每次迭代时产生一个新的宇宙来保存更新的结果,不对原宇宙进行交换。如果原始种群有200个宇宙,每次迭代经过黑洞/白洞交换策略新产生200个宇宙,经过向最优宇宙移动策略新产生约150个宇宙,最终对所有宇宙进行排序,取makespan较小的前200个宇宙进入下次迭代。宇宙更新策略算法流程如图 2所示。
|
图 2 宇宙更新策略算法流程 Fig. 2 The flow chart of universe update strategy algorithm |
标准的MVO算法在生成初始宇宙种群时,采用随机生成的方法。RHFS调度问题规模较大,寻优空间广泛,因此随机生成宇宙种群会导致算法效率低下、结果精确度不高等。使用4条启发式规则(LPT、SPT、FSPT、FLPT)和NEH启发式算法[19],加上局部搜索策略以及迭代贪婪算法对初始种群的生成进行改进,提高寻优效率和寻优精度。
2.3.1 启发式规则4条启发式规则中,LPT和SPT按照加工时长进行排序,前者优先处理加工总时长大的任务,后者反之。FSPT和FLPT按照在第1台机器上的加工时长对任务进行排序,前者在第1台机器上加工时长越短越先加工,后者反之。基于4条启发式规则分别生成了4个初始宇宙。
2.3.2 NEH启发式算法和局部搜索策略组合使用Nawaz等[19]提出了NEH启发式算法来解决置换流水车间调度问题。对于流水车间调度问题,基本的NEH启发式算法不一定能给出最短或者最优的加工序列,但可以在一定程度上保证加工序列的局部最优性。因此,将NEH启发式算法作为生成初始宇宙种群的方法之一。具体操作步骤如下。
Step1 首先计算各个工件完成加工所需的总加工时长, 然后根据计算得到的加工时长,将工件降序排列。
Step2 从Step1中取出前两个工件,找到一个加工顺序,使这两个工件最大完工时间最小,并保存此顺序。
Step3 对于工件i=3, 4, …, I,按顺序取出在Step1中按加工时长降序排列的第i个工件,把它插入Step2获得的加工顺序的所有可能位置,找到使最大完工时间最小的插入位置,并保存当前加工顺序。
Step4 继续Step3,直到完成Step1得到的加工序列中所有工件的插入,得到使整体最大完工时间最小的工件加工顺序。
利用NEH启发式算法和局部搜索策略组合使用的方式一共生成4个初始宇宙。
2.3.3 迭代贪婪算法迭代贪婪(iterated greedy, IG)是一种高效的启发式算法,具有实现简单、搜索效率高的特点,经常用于流水车间调度问题中。将IG算法作为生成初始宇宙种群的一种方式,其操作步骤如下。
Step1 设定需要取出的工件个数d。
Step2 对于一个初始工件加工顺序s0,随机删除s0中的n个工件,然后将删除的工件按删除的次序进行排列,得到一个删除工件顺序sn,剩余未删除的工件序列为sr。
Step3 对于sn中的工件i=1, 2, …, n,从sn中取出第i个工件,插入sr所有可能的位置,找到可以使优化目标值最小的位置,得到新的sr。
Step4 如果i < d,i=i+1, 否则终止操作。
使用IG算法得到了1个初始宇宙。
3 实验与分析使用Java语言进行编程,在Intel i5-1035G1 CPU 2.3GHz PC上运行。综合考虑种群多样性和计算量等因素,将虫洞存在的最小概率设置为0.2,最大概率设置为1,种群规模设置为200。在未使用启发式算法改进MVO算法时,200个初始宇宙都是随机生成的。在使用启发式算法改进MVO算法时,191个初始宇宙随机生成,其余9个初始宇宙,分别由4条启发式规则生成4个、NEH启发式算法和局部搜索策略组合使用生成4个以及IG算法生成1个。
在比较使用不同策略改进的MVO算法的最大完工时间时,设置最大迭代次数为1 000。为了方便表示,用MVO_1、MVO_2、MVO_3、和MVO_4分别代表离散的MVO算法、对向最优宇宙移动策略进行改进的MVO算法、使用NEH生成初始种群并对多元MVO算法的更新策略进行改进的MVO算法以及综合以上所有改进策略形成的算法。实验数据采用随机生成的方式。RHFS调度模式假定各个阶段都存在着相等数量的同构并行机, 为了简便,设Mj=1, L=2,但是所提算法也可以用于求解这两个参数等于其他值的情况。工件的释放、运输以及各个加工步骤的加工时长分别为在[1,]、[1,5]、[1,100]范围内均匀分布的随机数。根据I的取值来划分规划,I的4个取值100、70、50和20分别代表大规模、中规模、小规模以及极小规模问题,J的取值来自集合{40, 30, 20}。每组{I, J}随机产生10个实例,以便进行比较和分析,实验部分一共进行了120个实例的测试。
表 1列出了NEH、IG、GA、MVO算法以及改进的MVO算法的实验结果。其中,平均改进率α=(CMVO_1-CMVO_2)/CMVO_2*100%,平均改进率β=(CMVO_1-CMVO_3)/CMVO_3*100%,平均改进率γ=(CNEH-CMVO_4)/CMVO_4*100%。表中每种规模的结果均为10个实例在相同规模问题中的平均值,以反映其普遍特征。表 2列出了极小规模问题中MVO_1算法和NEH启发式算法的实验结果。
|
|
表 1 大、中、小规模问题的测试结果 Tab. 1 Test results for large, medium and small scale problems |
|
|
表 2 极小规模问题中MVO_1算法和NEH启发式算法实验结果 Tab. 2 Results of MVO_1 algorithm and NEH heuristic algorithm for minimal scale problems |
1) 在极小规模问题中,原始MVO算法的求解效率明显优于NEH启发式算法,但是在较大规模问题中,其求解能力却不及NEH启发式算法。因此,原始MVO算法在较大规模问题的求解中并不能发挥出最佳的作用。
2) 对于大规模问题,平均改进率α、β、γ分别为2.9%、10.6%、1.2%。对于小规模问题,α、β、γ分别为2.9%、8.6%、0.8%。使用改进策略的MVO算法的求解能力明显高于NEH启发式算法、IG算法以及原始MVO算法。
3) 就整体而言,在大规模问题中原始MVO算法对于目标值的求解能力低于NEH启发式算法,本文通过使用启发式算法以及改善MVO算法的更新策略,使MVO算法的求解能力得到明显提高,MVO算法的使用不再局限于小规模问题。
4) 为了分析本文提出的向最优宇宙移动策略对MVO算法的影响,引入了原始MVO算法(MVO_1)和改进向最优宇宙移动策略的MVO算法(MVO_2)的对比案例,并通过平均改进率表现其改进程度。结果表明,本文提出的向最优宇宙移动策略更适合于调度问题的MVO算法,相比于原始MVO算法能够取得更好的迭代较优解。
5) 将GA算法和MVO_4算法的实验结果进行比较,结果表明,所提算法对目标值的求解能力明显优于GA算法。
4 结语本文研究了以最小化最大完工时间为目标的半导体晶圆制造的调度问题,基于RHFS调度模型构建了一个整数规划模型,以解决半导体晶圆制造过程中的调度问题。同时,提出了适合于车间调度问题的改进MVO算法,从初始宇宙生成、宇宙更新策略、向最优宇宙移动策略等方面提高算法的性能。对比实验结果表明,所设计的算法在处理RHFS调度问题时有着显著的优势。本文算法重点在于最小化最大完工时间,但没有考虑算法的运行时间,未来的研究应该着重于如何有效地减少算法的运行时间,同时兼顾调度问题的其他目标。
| [1] |
PAN C R, ZHOU M C, QIAO Y, et al. Scheduling cluster tools in semiconductor manufacturing: recent advances and challenges[J]. IEEE transactions on automation science and engineering, 2018, 15(2): 586-601. DOI:10.1109/TASE.2016.2642997 (  0) 0) |
| [2] |
郭乘涛. 基于问题分解与蚁群算法的半导体晶圆制造系统调度方法的研究[D]. 上海: 上海交通大学, 2012. GUO C T. The research on scheduling of wafer fabrication system based on decomposition method and ant colony optimization algorithm[D]. Shanghai: Shanghai Jiaotong University, 2012. (  0) 0) |
| [3] |
董君, 叶春明. 具有学习效应的半导体晶圆制造绿色车间调度问题研究[J]. 运筹与管理, 2021, 30(4): 217-223. DONG J, YE C M. Research on green job shop scheduling problem of semiconductor wafers manufacturing with learning effect[J]. Operations research and management science, 2021, 30(4): 217-223. (  0) 0) |
| [4] |
LIN D P, LEE C K M. A review of the research methodology for the re-entrant scheduling problem[J]. International journal of production research, 2011, 49(8): 2221-2242. DOI:10.1080/00207541003720350 (  0) 0) |
| [5] |
LI L, HUO J Z, TANG O. A hybrid flowshop scheduling problem for a cold treating process in seamless steel tube production[J]. International journal of production research, 2011, 49(15): 4679-4700. DOI:10.1080/00207543.2010.495208 (  0) 0) |
| [6] |
周炳海, 钟臻怡. 可重入混合流水车间调度的拉格朗日松弛算法[J]. 控制理论与应用, 2015, 32(7): 881-886. ZHOU B H, ZHONG Z Y. Lagrangian relaxation algorithm for scheduling problems of reentrant hybrid flow shops[J]. Control theory & applications, 2015, 32(7): 881-886. (  0) 0) |
| [7] |
YING K C, LIN S W, WAN S Y. Bi-objective reentrant hybrid flowshop scheduling: an iterated Pareto greedy algorithm[J]. International journal of production research, 2014, 52(19): 5735-5747. DOI:10.1080/00207543.2014.910627 (  0) 0) |
| [8] |
轩华, 罗书敏, 王薛苑. 可重入混合流水车间调度的改进遗传算法[J]. 现代制造工程, 2019(2): 18-23. XUAN H, LUO S M, WANG X Y. An improved genetic algorithm for reentrant hybrid flow shop scheduling[J]. Modern manufacturing engineering, 2019(2): 18-23. (  0) 0) |
| [9] |
轩华, 李冰, 罗书敏, 等. 基于总加权完成时间的可重入混合流水车间调度问题[J]. 控制与决策, 2018, 33(12): 2218-2226. XUAN H, LI B, LUO S M, et al. Reentrant hybrid flowshop scheduling problem based on total weighted completion time[J]. Control and decision, 2018, 33(12): 2218-2226. (  0) 0) |
| [10] |
姚远远, 叶春明, 杨枫. 双目标可重入混合流水车间调度问题的离散灰狼优化算法[J]. 运筹与管理, 2019, 28(8): 190-199. YAO Y Y, YE C M, YANG F. Solving bi-objective reentrant hybrid flow shop scheduling problems by a hybrid discrete grey wolf optimizer[J]. Operations research and management science, 2019, 28(8): 190-199. (  0) 0) |
| [11] |
CHO H M, BAE S J, KIM J, et al. Bi-objective scheduling for reentrant hybrid flow shop using Pareto genetic algorithm[J]. Computers and industrial engineering, 2011, 61(3): 529-541. DOI:10.1016/j.cie.2011.04.008 (  0) 0) |
| [12] |
MIRJALILI S, MIRJALILI S M, HATAMLOU A. Multi-verse optimizer: a nature-inspired algorithm for global optimization[J]. Neural computing and applications, 2016, 27(2): 495-513. DOI:10.1007/s00521-015-1870-7 (  0) 0) |
| [13] |
WANG H F, HUANG M, WANG J W. An effective metaheuristic algorithm for flowshop scheduling with deteriorating jobs[J]. Journal of intelligent manufacturing, 2019, 30(7): 2733-2742. DOI:10.1007/s10845-018-1425-8 (  0) 0) |
| [14] |
王瑞. 云计算环境下任务调度策略的研究[D]. 赣州: 江西理工大学, 2021. WANG R. Research on task scheduling strategy in cloud computing environment[D]. Ganzhou: Jiangxi University of Science and Technology, 2021. (  0) 0) |
| [15] |
葛续涛. 计及多目标的社区综合能源系统优化调度[D]. 青岛: 青岛大学, 2021. GE X T. Optimal dispatch of community comprehensive energy system considering multi-objective[D]. Qingdao: Qingdao University, 2021. (  0) 0) |
| [16] |
黄辉. 热轧混合流水车间调度方法及仿真系统研究[D]. 重庆: 重庆大学, 2021. HUANG H. Study on scheduling method and simulation system of hot rolling hybrid flow workshop[D]. Chongqing: Chongqing University, 2021. (  0) 0) |
| [17] |
赵世杰, 高雷阜, 徒君, 等. 耦合横纵向个体更新策略的改进MVO算法[J]. 控制与决策, 2018, 33(8): 1422-1428. ZHAO S J, GAO L F, TU J, et al. Improved multi verse optimizer coupling horizontal-and-vertical individual updated strategies[J]. Control and decision, 2018, 33(8): 1422-1428. (  0) 0) |
| [18] |
张强, 姜慧清, 王颖, 等. 基于离散多元宇宙算法求解车辆路径问题[J]. 电子科技大学学报, 2021, 50(6): 890-898. ZHANG Q, JIANG H Q, WANG Y, et al. Solving vehicle routing problem with fuzzy time window based on discrete multiverse algorithm[J]. Journal of university of electronic science and technology of China, 2021, 50(6): 890-898. (  0) 0) |
| [19] |
NAWAZ M, ENSCORE E E, HAM I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem[J]. Omega, 1983, 11(1): 91-95. DOI:10.1016/0305-0483(83)90088-9 (  0) 0) |
 2024, Vol. 56
2024, Vol. 56


