2. 许继电气股份有限公司 河南 许昌 461000;
3. 郑州市区块链与数据智能重点实验室 河南 郑州 450002;
4. 中国石油化工股份有限公司中原油田分公司 信息化管理中心 河南 濮阳 457001
2. XJ Electric Co., Ltd, Xuchang 461000, China;
3. Zhengzhou Key Laboratory of Blockchain and Data Intelligence, Zhengzhou 450002, China;
4. Information Management Center, Zhongyuan Oilfield Branch of SINOPEC, Puyang 457001, China
三维重建是计算机视觉领域中非常重要的研究方向之一,其中基于视觉的三维重建是该领域的研究热点。基于视觉的三维重建通过各种仪器或者相机设备,对真实的场景和目标物体进行扫描或拍摄,然后采用计算机算法加以处理,对物体的三维空间信息进行深入的解析,最终逆向求取空间点坐标,得到三维立体表面模型。经过四五十年的研究与发展,基于视觉的三维重建日益成熟,新技术层出不穷,逐渐应用于工业、医疗、交通、军事等诸多领域,在工业检测、医学影像、无人驾驶、军事探测等方面发挥着重大作用。
基于视觉的三维重建由于其适用领域和应用场景的不同,形成了不同的技术路线。随着研究的不断深入,基于视觉的三维重建技术通常可划分为基于主动视觉的三维重建和基于被动视觉的三维重建。其中,主动视觉方法主要利用相关仪器扫描目标物体,通过调整自身参数发射激光、声波、脉冲等信号,然后分析发出和接收结构声光信号的时间差等数据,确定目标物体的距离、大小、形状等三维结构的细节信息,最后精确地还原物体或场景的三维模型。而被动视觉自身并不会发射任何能量信号来收集目标信息,而是完全依靠自然光源下目标物体或场景对光照的漫反射效应,通过收集图像的二维深度信息来完成检测。相比之下,主动视觉方法在实际操作上存在较高的难度,可行性较低,难以很好地适应复杂环境,局限性比较大。而基于被动视觉的三维重建技术可操作性强,成本较低,适用于各种复杂环境中目标物体的三维重建,在实际应用中更为广泛。因此,本文对基于被动视觉的三维重建技术研究进展进行了整理和分析。基于被动视觉的三维重建技术根据采集装置的数量进行分类,可分为单目视觉法、双目视觉法和多目视觉法;根据不同应用方法进行分类,可分为运动恢复结构法和深度学习法。
1 根据采集装置数量分类根据获取二维图像数据所采用的采集装置数量,基于被动视觉的三维重建技术可以分为单目视觉法、双目视觉法和多目视觉法。
1.1 单目视觉法单目视觉法只采用一台摄像机进行数据采集,采集的数据可以为单幅图像或者多幅图像。单目视觉法三维重建流程如图 1所示。
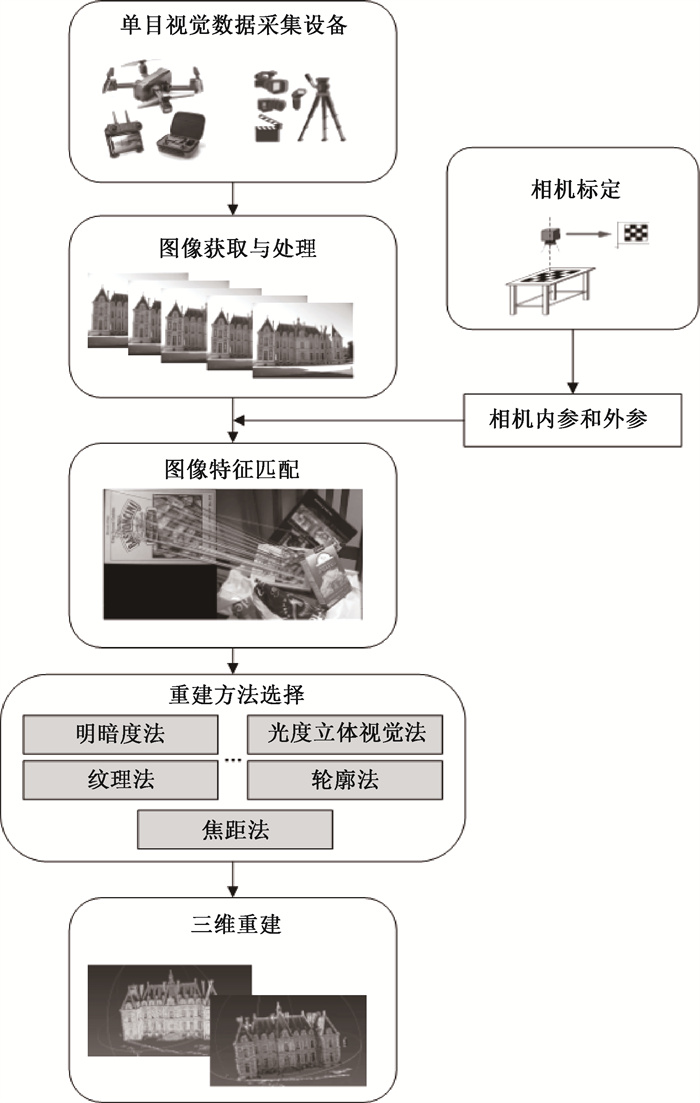
|
图 1 单目视觉法三维重建流程 Fig. 1 3D reconstruction process of monocular vision |
单目视觉法首先采用单目相机等装置采集图像数据,然后获取图像特征信息,通过算法进行特征信息匹配,最后选取合适的重建方法得到三维重建模型。从单目相机拍摄二维图像中的某一点到三维立体模型空间点的转换原理可表示为
| $ \left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{array}\right] \cdot\left[\begin{array}{cc} \boldsymbol{R} & \boldsymbol{t} \\ 0 & 1 \end{array}\right] \cdot\left[\begin{array}{c} X_w \\ Y_w \\ Z_w \\ 1 \end{array}\right], $ | (1) |
其中:(u, v)表示在图像坐标系下图像点的坐标;(Xw, Yw, Zw)表示空间中物体的三维坐标;R和t分别表示旋转矩阵和平移向量;(u0, v0)为摄像头的中心点在二维图像中的坐标;fx和fy分别为摄像机在x和y方向上的焦距。通过式(1)可以求出空间中任意一点的三维坐标。
单目视觉三维重建技术包括以下5种方法。
1) 明暗度法。明暗度法即明暗度恢复形状法。该方法主要对图像中由光源照射所产生的明暗阴影变化进行分析,借助反射光照模型计算物体表面的梯度场,由梯度场进行积分运算,最后得到物体表面高度值。Horn[1]于1970年第一次提出明暗度法的概念,推导出了明暗度方程。Ahmed等[2]利用Lax-Friedrichs sweeping算法对混合表面采用明暗度法进行求解,并建立了Ward模型下混合表面图像辐照度方程。Vogel等[3]提出了基于非朗伯特模型的明暗度法,取得了良好的效果。为提高求解效率、降低重建误差,王国珲等[4]改进了Ward模型,建立了透视投影下的辐照度方程,提出了基于牛顿-拉弗森法的混合表面快速三维重建求解算法。
2) 光度立体视觉法。光度立体视觉法是利用目标物体在各种光线环境下拍摄得到的图像数据,重建该物体表面的立体结构。Woodham[5]对明暗度法进行改进,提出了光度立体视觉法,改善了单幅图像中所包含的重建信息较少的问题。2010年,Shi等[6]提出了自标定的光度立体视觉法。2018年,Santo等[7]提出了深度光度立体网络,通过使用深度神经网络在复杂的反射率观测值和表面法线之间建立灵活的映射,使得重建效果更加显著。2020年,陈明汉等[8]提出了一种基于多尺度卷积网络架构的光度立体视觉算法,极大提高了对非朗伯表面的适应性。
3) 纹理法。纹理法的基本理论为:物体表面均具备不同的纹理信息,这些信息由纹理元组成,当物体被投射在图像上,根据纹理元可以确定表面方向,通过计算能够获取深度数据,恢复立体结构。Clerc等[9]于2002年使用小波变换进行改进,完成了纹理分析。2010年,Warren等[10]对正交投影解不唯一的问题进行了调整,采用透视投影模型进行纹理法重建实验,使重建效果得到了提升。
4) 轮廓法。轮廓法即轮廓恢复形状法。该方法通过对物体进行多角度拍摄,然后提取图像中目标物体的轮廓数据,逆向推导出物体的三维结构。主流轮廓法是融合了体素、视壳和锥素的重建方法。2006年,Forbes等[11]实现了直接从物体的轮廓及其反射计算焦距、主点、镜子和相机姿势,从未标定的图像中生成视壳。2020年,Jang等[12]通过重复计算视壳的残差来处理凹面区域,并生成分层数据结构即可视外壳树,解决了凹面区域的细节展示。
5) 焦距法。焦距法即焦点恢复形状法,于1997年由Rajagopalan等[13]首次提出。焦距法需要精确计算聚焦量以及判断噪声对清晰度的影响。考虑焦距变化所产生的视差,Sahay等[14]对焦距法进行了改进。康宇等[15]针对焦距法内存空间占用量大的问题,提出一种基于扩散的聚焦形貌恢复算法,通过对聚焦评价曲线区间进行约束,降低了内存使用率。赵洪盛等[16]提出一种图像噪声检测算法,通过滤波构建无噪声图像序列,进一步提升了焦距法的精确度。
表 1对比了上述5种单目视觉三维重建技术,罗列了各种方法的优缺点以及重建效果,同时对具体应用场景进行了简要说明。可以看出,单目视觉法通过单张或较少数量的图像即可完成目标物体的重建,重建速度快、效率高,但对于光照等因素的依赖较为严重;同时,重建效果存在表面残缺、空洞等现象,依然有很大的改善空间。
|
|
表 1 单目视觉三维重建技术对比 Tab. 1 Comparison of 3D reconstruction techniques based on monocular vision |
双目视觉法,也被称为立体视觉法,能够将双目视差信息转换为物体深度信息。该方法主要采用双目摄像机获取双视图图像,然后利用立体匹配计算原理获得视差图,最后利用三角测量的方法对匹配点的视差信息进行转换,得到物体表面的三维坐标,恢复三维立体模型结构。
根据摄像机摆放位置的不同,双目视觉三维重建可以分为平行式光轴三维重建方法[17]和汇聚式光轴三维重建方法[18]。平行式光轴和汇聚式光轴分别如图 2、图 3所示。
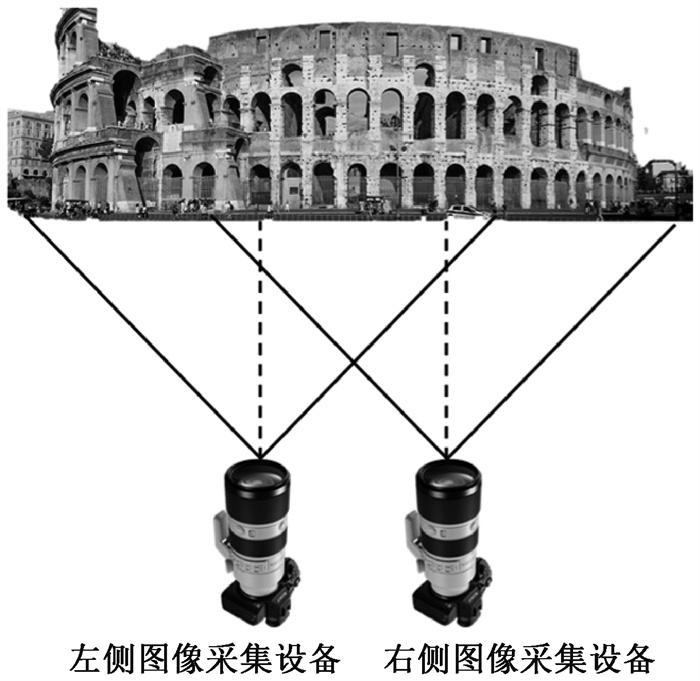
|
图 2 平行式光轴 Fig. 2 Parallel optical axis |
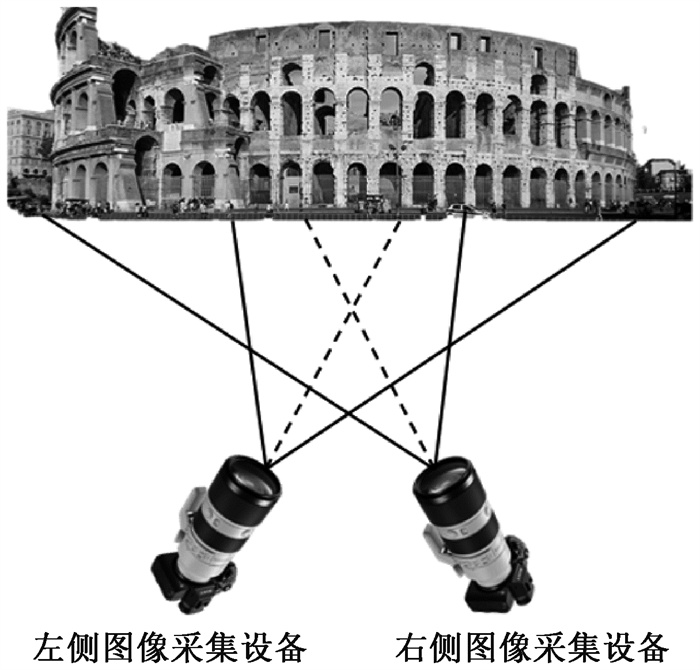
|
图 3 汇聚式光轴 Fig. 3 Convergent optical axis |
平行式光轴和汇聚式光轴三维重建方法的具体情况如下。
1) 平行式光轴三维重建方法。该方法的设备面向目标结构平行放置,保证光轴也与水平方向平行,能够形成平行的成像平面。两台摄像机只存在光轴位置的左右差异,能很好地实现图像的立体匹配。
2) 汇聚式光轴三维重建方法。汇聚式光轴双目视觉三维重建方法在平行式光轴双目视觉系统的基础上,左右两台摄像机分别绕光心旋转,使两者向内呈八字。该方法的优势是能够扩大图像采集设备的视野角度。
Hirschmuller[19]首次提出了半全局匹配算法,成为当下最流行的立体视觉算法之一。Michael等[20]提出了对该算法参数化的直接扩展,提升了半全局匹配算法的准确性。随着神经网络和深度学习的普及和发展,Bontar等[21]将卷积神经网络与立体匹配算法相结合,提出一种从校正后图像对中提取深度信息的方法,通过训练卷积神经网络来预测两个图像块的匹配程度。Lu等[22]提出一种级联多尺度和多维网络的架构,将传统方法的代价聚合考虑在内,取得了良好的效果。双目视觉方法整体上已经比较成熟,广泛应用于现代化人工智能领域,如电缆巡检机器人[23]等自动化无人设备。
1.3 多目视觉法多目视觉法是对双目视觉进行扩展所形成的方法,采用3个或3个以上的摄像机获取图像,其研究难点在于视差图信息匹配。2003年,雷成等[24]研发了CVSuit三维重建系统。之后,翟振刚[25]对立体匹配算法进行研究,提出一种自适应区域立体匹配算法。Zhang等[26]将基于多视觉的三维重建分为3个阶段,提出了中心线匹配配准算法来实现对管道的重构。Bai等[27]将多目视觉法运用于无人机地质灾害检测,获得精准的三维地形模型。陈星等[28]结合神经网络和特征金字塔结构,对多尺度融合立体匹配算法进行改进,可以得到效果良好的视差图。
2 根据不同应用方法分类基于被动视觉的三维重建在不同领域所运用的重建方法有所差异,其达到的重建效果也各有不同,从而体现出相应的优缺点。根据其应用方法进行分类,可以分为运动恢复结构法和深度学习法。
2.1 运动恢复结构法运动恢复结构法(structure from motion,SfM)是通过分析多视角二维图像信息,求解三维立体模型数据的方法。由于涉及拍摄过程中相机多角度的移动,因此被称为运动恢复结构。SfM三维重建流程如图 4所示。
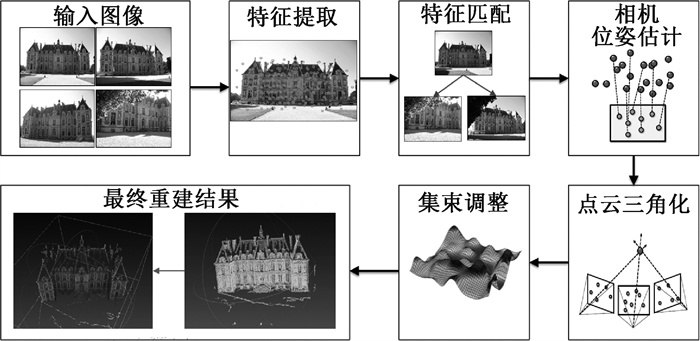
|
图 4 SfM三维重建流程 Fig. 4 3D reconstruction process of SfM |
目前主流的SfM方法可分为增量式[29]和全局式两大类型。
增量式SfM的原理是通过摄像机获取多角度图像,选取两张图像初始化,然后不断加入新的图像进行迭代,对于初始化的图像以及不断添加的图像一边进行三角化生成三维点,一边进行局部优化,最终实现整个图像的三维重建过程。
全局式SfM是由Sturm等[30]率先提出的,其原理是一次性地对所有的图像计算匹配关系生成三维点,最后进行整体优化。2011年,Crandall等[31]提出一种基于离散马尔可夫随机场的混合离散连续优化的全局式SfM。2015年,Cui等[32]在已有理论的基础上提出一种全新的全局式SfM,使其处理数据更加多样化。
2.2 深度学习法深度学习法三维重建的过程可以理解为对函数的拟合,通过神经网络训练将图像的像素信息转化为因变量物体的深度信息,从二维图像中恢复物体的三维结构。Sermanet等[33]提出了使用卷积网络对图像进行分类、定位和检测的框架,实现了在ConvNet中多尺度和滑动窗口的方法。随后,Eigen等[34]使用两个深度网络堆栈的方法预测场景三维信息,其中一个深度网络对图像进行全局预测,另一个对预测信息进行局部细化。张冀等[35]提出一种基于多尺度CNN-RNN的单图三维重建网络,通过高斯金字塔模型构建多尺度网络,使得二维图像的特征提取更加充分,提高了重建精度。
3 对比与分析基于被动视觉的三维重建技术的对比结果如表 2所示。
|
|
表 2 基于被动视觉的三维重建技术对比 Tab. 2 Comparison of 3D reconstruction techniques based on passive vision |
基于单目视觉的重建方法较为多样,但各有其局限性,易受光照条件、噪声、纹理特征等因素的影响;基于双目视觉和多目视觉的重建方法,其稳定性比单目视觉法要高,技术相对成熟,能够实现较高的重建精度,但在复杂场景及恶劣环境下,设备更为昂贵且操作复杂,普适性较差。运动恢复结构法可以结合单目视觉法,通过使用多张图像达到更好的重建效果,但图像数量增加也会增大计算量,降低三维重建的效率。深度学习法作为新兴的三维重建技术,与传统的方法有所区别,其通过神经网络训练可以重建出较为精确的三维模型,但重建的质量依赖于训练过程,需要不断地调整网络框架,同时对数据集较为敏感。
4 小结与展望本文根据采集装置数量和应用方法的不同,对主流的基于被动视觉的三维重建技术进行了梳理、分类和对比分析。三维重建技术目前主要存在以下问题:
1) 运算量问题。为提高重建精度增加了图像数量,导致计算量过于庞大,重建时间长,对于硬件资源的需求过高。
2) 鲁棒性问题。部分三维重建技术的抗干扰能力差,易受外界各种自然因素的影响。
3) 重建效率问题。部分重建过程耗时较长,降低了整体的重建效率。
随着研究的深入,上述问题的解决并不局限于原有方法的直接优化或提升,可通过各类新方法、新技术的融合进行解决。综上,基于被动视觉的三维重建技术方兴未艾,有必要基于目前的众多方法进行组合、优化与创新。随着各类新方法的加入,三维重建技术必定能更好地服务于人类社会的生产和生活。
| [1] |
HORN B K. Shape from shading: a method for obtaining the shape of a smooth opaque object from one view[D]. Cambridge: Massachusetts Institute of Technology, 1970.
(  0) 0) |
| [2] |
AHMED A H, FARAG A A. Shape from shading under various imaging conditions[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2007: 1-8.
(  0) 0) |
| [3] |
VOGEL O, BREUß M, WEICKERT J. Perspective shape from shading with non-lambertian reflectance[C]//Joint Pattern Recognition Symposium. Berlin: Springer Press, 2008: 517-526.
(  0) 0) |
| [4] |
王国珲, 张璇. 透视投影下混合表面3D重建的快速SFS算法[J]. 光学学报, 2021, 41(12): 179-187. WANG G H, ZHANG X. Fast shape-from-shading algorithm for 3D reconstruction of hybrid surfaces under perspective projection[J]. Acta optica sinica, 2021, 41(12): 179-187. (  0) 0) |
| [5] |
WOODHAM R J. Photometric method for determining surface orientation from multiple images[J]. Optical engineering, 1980, 19(1): 139-144. (  0) 0) |
| [6] |
SHI B X, MATSUSHITA Y, WEI Y C, et al. Self-calibrating photometric stereo[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2010: 1118-1125.
(  0) 0) |
| [7] |
SANTO H, SAMEJIMA M, SUGANO Y, et al. Deep photometric stereo network[C]//Proceedings of the IEEE International Conference on Computer Vision Workshops. Piscataway: IEEE Press, 2018: 501-509.
(  0) 0) |
| [8] |
陈明汉, 任明俊, 肖高博, 等. 基于多尺度卷积网络的非朗伯光度立体视觉方法[J]. 中国科学: 技术科学, 2020, 50(3): 323-334. CHEN M H, REN M J, XIAO G B, et al. Non-Lambertian photometric stereo vision algorithm based on a multi-scale convolution deep learning architecture[J]. Scientia sinica: technologica, 2020, 50(3): 323-334. (  0) 0) |
| [9] |
CLERC M, MALLAT S. The texture gradient equation for recovering shape from texture[J]. IEEE transactions on pattern analysis and machine intelligence, 2002, 24(4): 536-549. DOI:10.1109/34.993560 (  0) 0) |
| [10] |
WARREN P A, MAMASSIAN P. Recovery of surface pose from texture orientation statistics under perspective projection[J]. Biological cybernetics, 2010, 103(3): 199-212. DOI:10.1007/s00422-010-0389-3 (  0) 0) |
| [11] |
FORBES K, NICOLLS F, JAGER G, et al. Shape-from-Silhouette with two mirrors and an uncalibrated camera[C]//Proceedings of the 9th European Conference on Computer Vision. New York: ACM Press, 2006: 165-178.
(  0) 0) |
| [12] |
JANG T Y, KIM S D, HWANG S S. Visual hull tree: a new progressive method to represent voxel data[J]. IEEE access, 2020, 8: 141850-141859. DOI:10.1109/ACCESS.2020.3013300 (  0) 0) |
| [13] |
RAJAGOPALAN A N, CHAUDHURI S. A variational approach to recovering depth from defocused images[J]. IEEE transactions on pattern analysis and machine intelligence, 1997, 19(10): 1158-1164. DOI:10.1109/34.625126 (  0) 0) |
| [14] |
SAHAY R R, RAJAGOPALAN A N. Dealing with parallax in shape-from-focus[J]. IEEE transactions on image processing, 2011, 20(2): 558-569. DOI:10.1109/TIP.2010.2066983 (  0) 0) |
| [15] |
康宇, 陈念年, 范勇, 等. 基于扩散的聚焦形貌恢复算法[J]. 计算机工程, 2016, 42(3): 259-265. KANG Y, CHEN N N, FAN Y, et al. Shape from focus algorithm based on spreading[J]. Computer engineering, 2016, 42(3): 259-265. (  0) 0) |
| [16] |
赵洪盛, 丁华, 刘建成. 基于图像区域像素重构的聚焦形貌恢复[J]. 计算机工程, 2019, 45(2): 233-239. ZHAO H S, DING H, LIU J C. Shape from focus based on image regional pixel reconstruction[J]. Computer engineering, 2019, 45(2): 233-239. (  0) 0) |
| [17] |
ZOU X J, ZOU H X, LU J. Virtual manipulator-based binocular stereo vision positioning system and errors modelling[J]. Machine vision and applications, 2012, 23(1): 43-63. DOI:10.1007/s00138-010-0291-y (  0) 0) |
| [18] |
李占贤, 许哲. 双目视觉的成像模型分析[J]. 机械工程与自动化, 2014(4): 191-192. LI Z X, XU Z. Analysis of imaging model of binocular vision[J]. Mechanical engineering & automation, 2014(4): 191-192. (  0) 0) |
| [19] |
HIRSCHMULLER H. Accurate and efficient stereo processing by semi-global matching and mutual information[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2005: 807-814.
(  0) 0) |
| [20] |
MICHAEL M, SALMEN J, STALLKAMP J, et al. Real-time stereo vision: optimizing semi-global matching[C]//Proceedings of the IEEE Intelligent Vehicles Symposium. Piscataway: IEEE Press, 2013: 1197-1202.
(  0) 0) |
| [21] |
BONTAR J, LECUN Y. Computing the stereo matching cost with a convolutional neural network[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2015: 1592-1599.
(  0) 0) |
| [22] |
LU H H, XU H, ZHANG L, et al. Cascaded multi-scale and multi-dimension convolutional neural network for stereo matching[C]//Proceedings of the IEEE Visual Communications and Image Processing. Piscataway: IEEE Press, 2019: 1-4.
(  0) 0) |
| [23] |
HUANG L, WU G P, LIU J Y, et al. Obstacle distance measurement based on binocular vision for high-voltage transmission lines using a cable inspection robot[J]. Science progress, 2020, 103(3): 1-35. (  0) 0) |
| [24] |
雷成, 胡占义, 吴福朝, 等. 一种新的基于Kruppa方程的摄像机自标定方法[J]. 计算机学报, 2003, 26(5): 587-597. LEI C, HU Z Y, WU F C, et al. A novel camera self-calibration technique based on the Kruppa equations[J]. Chinese journal of computers, 2003, 26(5): 587-597. (  0) 0) |
| [25] |
翟振刚. 立体匹配算法研究[D]. 北京: 北京理工大学, 2010. ZHAI Z G. Research on stereo matching algorithm[D]. Beijing: Beijing Institute of Technology, 2010. (  0) 0) |
| [26] |
ZHANG T, LIU J H, LIU S L, et al. A 3D reconstruction method for pipeline inspection based on multi-vision[J]. Measurement, 2017, 98: 35-48. (  0) 0) |
| [27] |
BAI S H, BAI S Y. Application of unmanned aerial vehicle multi-vision image 3D modeling in geological disasters[J]. Journal of information and optimization sciences, 2017, 38(7): 1101-1115. (  0) 0) |
| [28] |
陈星, 张文海, 侯宇, 等. 改进的基于多尺度融合的立体匹配算法[J]. 西北工业大学学报, 2021, 39(4): 876-882. CHEN X, ZHANG W H, HOU Y, et al. Improved stereo matching algorithm based on multi-scale fusion[J]. Journal of northwestern polytechnical university, 2021, 39(4): 876-882. (  0) 0) |
| [29] |
WU C C. Towards linear-time incremental structure from motion[C]//Proceedings of the International Conference on 3D Vision. Piscataway: IEEE Press, 2013: 127-134.
(  0) 0) |
| [30] |
STURM P, TRIGGS B. A factorization based algorithm for multi-image projective structure and motion[M]//Lecture Notes in Computer Science. Berlin: Springer Press, 1996: 709-720.
(  0) 0) |
| [31] |
CRANDALL D, OWENS A, SNAVELY N, et al. Discrete-continuous optimization for large-scale structure from motion[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2011: 3001-3008.
(  0) 0) |
| [32] |
CUI H N, SHEN S H, GAO W, et al. Efficient large-scale structure from motion by fusing auxiliary imaging information[J]. IEEE transactions on image processing, 2015, 24(11): 3561-3573. (  0) 0) |
| [33] |
SERMANET P, EIGEN D, ZHANG X, et al. Overfeat: integrated recognition, localization and detection using convolutional networks[EB/OL]. (2014-02-24)[2022-09-12]. https://arxiv.org/pdf/1312.6229v4.pdf.
(  0) 0) |
| [34] |
EIGEN D, PUHRSCH C, FERGUS R. Depth map prediction from a single image using a multi-scale deep network[EB/OL]. (2014-06-09)[2022-09-12]. https://doi.org/10.48550/arXiv.1406.2283.
(  0) 0) |
| [35] |
张冀, 郑传哲. 基于多尺度CNN-RNN的单图三维重建网络[J]. 计算机应用研究, 2020, 37(11): 3487-3491. ZHANG J, ZHENG C Z. 3D reconstruction network based on multi-scale CNN-RNN[J]. Application research of computers, 2020, 37(11): 3487-3491. (  0) 0) |
 2024, Vol. 56
2024, Vol. 56


