2. 山东省智慧矿山信息技术重点实验室 山东 青岛 266590
2. Key Laboratory of Wisdom Mine Information Technology of Shandong Province, Qingdao 266590, China
聚类是数据挖掘领域的重要研究内容之一,在识别数据的内在结构方面具有极其重要的作用.文献[1-4]对相关算法进行了研究.划分方法中经典的有K-means算法[5]、K-medoids算法[6]等;层次方法中经典的有CHAMELEON算法[7]、BIRCH算法[8]等;基于密度的方法中经典的有DBSCAN算法[9]、OPTICS算法[10]等;基于网格的方法中经典的有STING算法[11]等.
近几年,研究者从不同角度提出了许多优秀的算法.例如,文献[12]将密度的思想和距离相结合,提出一种快速的密度峰值聚类(DPC)算法.文献[13-14]在DPC算法的基础上,提出两种基于K近邻的样本分配策略.文献[15]提出一种基于数据点间信息传递的聚类算法(AP).针对数据的不平衡问题,文献[16]将概率模型选择和参数优化估计的方法用于聚类,算法在不平衡数据集上有很好的表现.此外,图论的很多方法也被用来解决聚类问题.例如,文献[17]对基于最小生成树的图论聚类方法进行了分析.文献[18]采用生成两轮最小生成树的方法,能够对各种大小、形状和密度的数据实现聚类.文献[19]将最小生成树应用于数据的分割和合并过程,提出一种新的层次聚类算法.本文在相似性计算方法的基础上,提出了一种新的非度量距离计算方法,利用最小生成树的方法实现数据的聚类.算法设计简单,易于实现,同时可以聚类任意形状数据和兼容处理不均衡数据.对于连通性较好的数据,算法具有很好的聚类效果.
1 算法的理论基础 1.1 互近邻相对距离距离计算是很多学习任务的基本问题.闵可夫斯基距离提供了距离计算的一般形式,这类距离被称为度量距离.此外还有非度量距离,互近邻距离(mutual neighbor distance)就是其中一种.
| $MND({x_i},{x_j}) = NN({x_i},{x_j}) + NN({x_j},{x_i}),$ |
式中:NN(xi, xj)表示xi是xj的第几近邻点; MND(xi, xj)表示xi与xj的互近邻距离.显然有MND(xi, xj)=MND(xj, xi).
互近邻距离相对于度量距离有很多优点.为了将互近邻距离与度量距离的优点相结合,本文提出互近邻相对距离(mutual neighbor relative distance)的概念.
首先给出基距离(base distance)的定义为
| $BD({x_i},k) = \frac{1}{k}\sum\limits_{j = 1}^k {d({x_i},{x_j}),} $ |
式中:d(xi, xj)表示xi与xj之间的某种距离,如常用的欧氏距离;BD(xi, k)表示xi的k近邻基距离,代表了xi的距离衡量标准.本文采用k=n,此时将xi的基距离简记为BD(xi).
互近邻相对距离的定义为
| $MNRD({x_i},{\rm{ }}{x_j}) = NNR({x_i},{\rm{ }}{x_j}) + NNR({x_j},{\rm{ }}{x_i}),$ |
式中:
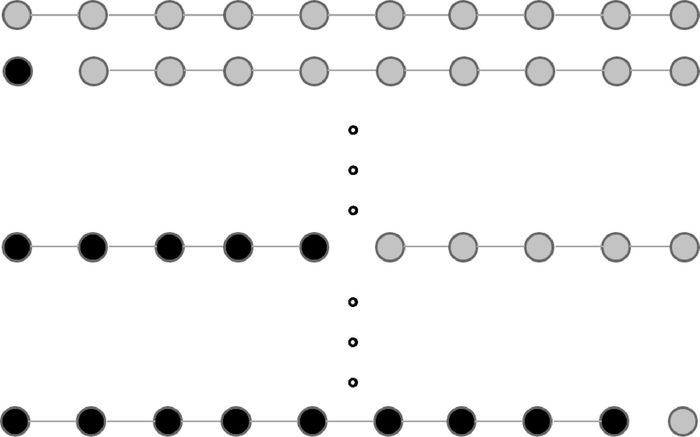
许多优化问题都可以转化为求解最小生成树问题[22].最小生成树也被广泛应用于旅行商[23]、文本聚类[24]、基因表达数据分析[25]等领域.最小生成树聚类的第一步是构建最小生成树,图的节点对应于被分析数据的最小单元,图的边(或弧)对应于处理数据之间的相似性度量.比较经典的最小生成树求解算法有prim算法和kruskal算法,其中prim算法适用于边较多的情况.得到最小生成树后,需要对最小生成树进行分割.若聚成k个簇,则需要k-1次分割.对于有n个结点的最小生成树,共包含n-1条边.一般的分割策略是搜索权重最大(相似性最小)的边进行分割,但是这种分割不能解决数据的不平衡问题.不同的分割策略如图 1所示,虽然图中最小生成树的各边权重相同,但是考虑到平衡问题,对不同边进行分割的结果显然并不相同.
|
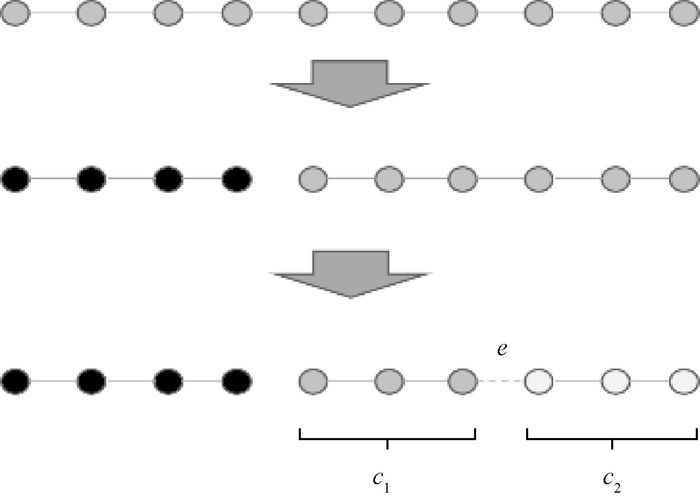
图 1 不同的分割策略 Figure 1 Different segmentation strategies |
考虑到分割后数据的不平衡问题,需要引入平衡度的定义.数据集D包含n条数据,设分割某条边e后新形成两个簇为C1和C2,用a和b分别表示两个簇中包含样本的个数,并且a≤b,则边e的平衡度的计算公式为
| ${p_e} = \frac{a}{b} \times \frac{{a + b}}{n}.$ |
另外,数据本身也可能是不平衡的,因此需要引入平衡估计参数p,平衡估计参数根据先验知识设定.加入参数p后,相应平衡度调整公式为
| ${p_e}^{'} = \left\{ {\begin{array}{*{20}{l}} {{p_e}/p,}&{0 < {p_e} \le p,}\\ {1 - {p_e} + p,}&{p < {p_e} \le 1.} \end{array}} \right.$ |
平衡度的计算如图 2所示,最小生成树共包含10个样本点,若设p=0.6,计算得到pe=1.
|
图 2 平衡度的计算 Figure 2 Calculation of equilibrium degree |
将边界权重和平衡度的乘积作为分割参数,在最小生成树分割的过程中,每次选择分割参数最大的边.经过多次分割,最终实现聚类.
2 算法描述算法的核心是相似性矩阵的计算和最小生成树的分割.聚类算法的过程如下:
输入:数据集D,平衡参数p,簇的个数k;
输出:聚类结果.
1:利用互近邻相对距离计算距离矩阵G.
2:使用prim算法计算得到最小生成树T;最小生成树中边的权重向量为VT.
3:计算最小生成树中每条边的平衡度,生成向量PT.
4:进行k-1轮迭代.
5:VPT=VT.*PT;%“.*”表示对应相乘.
6:找到VPT中的最大值对应的边e;将边e从T中删除.
7:从VT中删除边e对应的权重;计算并更新PT.
8:根据T的划分,将数据集D划分成k个簇.
算法主要由以下三部分组成:根据互近邻相对距离得到邻接矩阵,其时间复杂度为O(n2);求解最小生成树,假设是邻接矩阵的存储方式,最大时间复杂度为O(n2);分割最小生成树,分割之前需要计算平衡度,因此需要统计边两端的子树分别包含多少点.子树包含点的信息可以事先计算存储,边分割后运行更新即可.分割最小生成树的时间复杂度为O(n).
3 实验与结果实验分为人工数据集实验和真实数据集实验两部分.对比算法分别为DPC、AP、DBSCAN、K-means、CHAMELEON和2-MSTClus[18].其中K-means算法调用Matlab中的库函数,其他算法采用作者提供的源码或程序.聚类效果判断标准采用ACC、AMI和ARI评价指标.3种指标的取值上界为1,取值越大表示聚类结果越好.对于真实数据本文进行了预处理,均归一化到[0, 1].实验所用人工数据集和真实数据集如表 1和表 2所示.
|
|
表 1 人工数据集 Table 1 Artificial data sets |
|
|
表 2 真实数据集 Table 2 Real data sets |
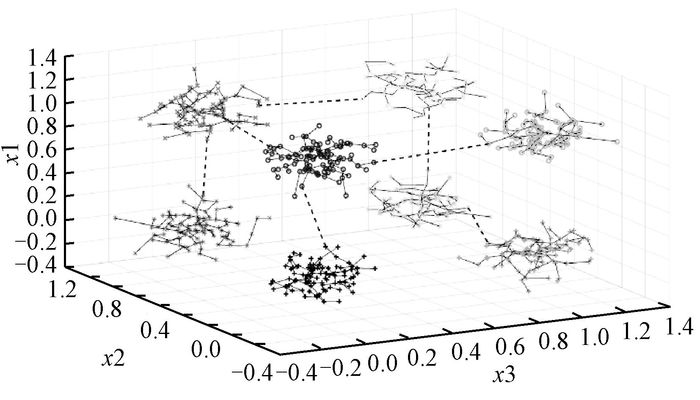
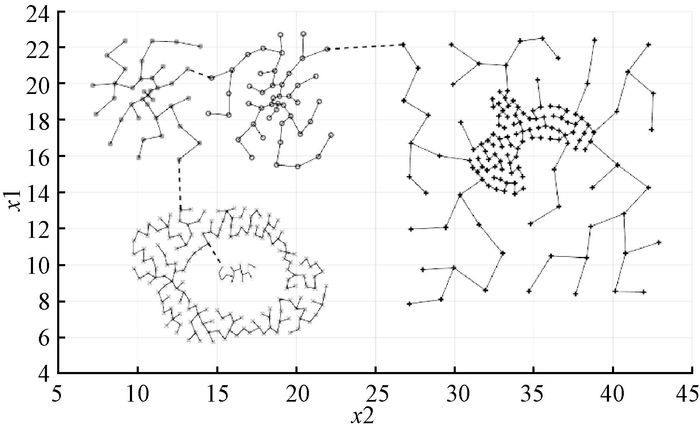
人工数据集为2维或3维数据,方便可视化.在人工数据集上进行测试,聚类结果以图的方式展示,不同灰度和形状的数据代表不同的簇.聚类数据会有多种形式,其中比较容易聚类的是明显分离的数据,如图 3和图 4所示.对于比较复杂的数据,算法也可以很好地实现聚类,如图 5~图 8所示.

|
图 3 Twenty数据集聚类结果 Figure 3 Clustering results of Twenty data set |
|
图 4 Hypercube数据集聚类结果 Figure 4 Clustering results of Hypercube data set |
|
图 5 Compound数据集聚类结果 Figure 5 Clustering results of Compound data set |
|
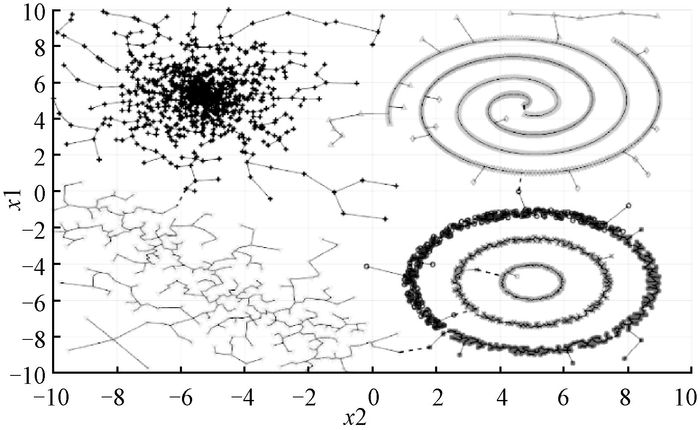
图 6 Impossible数据集聚类结果 Figure 6 Clustering results of Impossible data set |
|
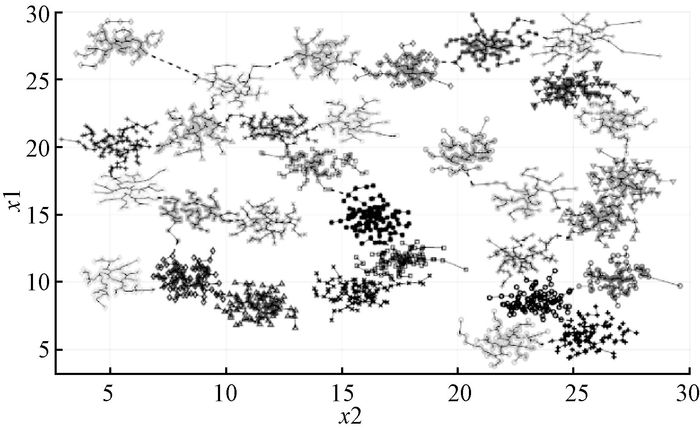
图 7 D31数据集聚类结果 Figure 7 Clustering results of D31 data set |
|
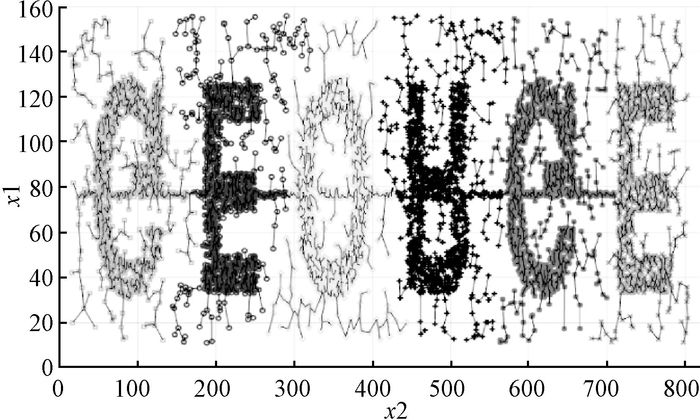
图 8 Q58数据集聚类结果 Figure 8 Clustering results of Q58 data set |
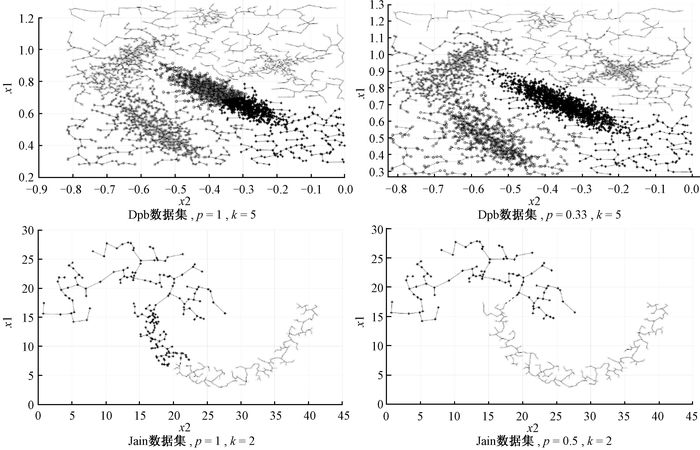
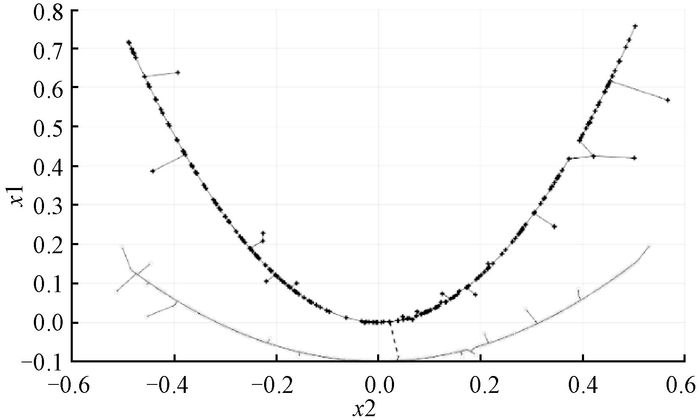
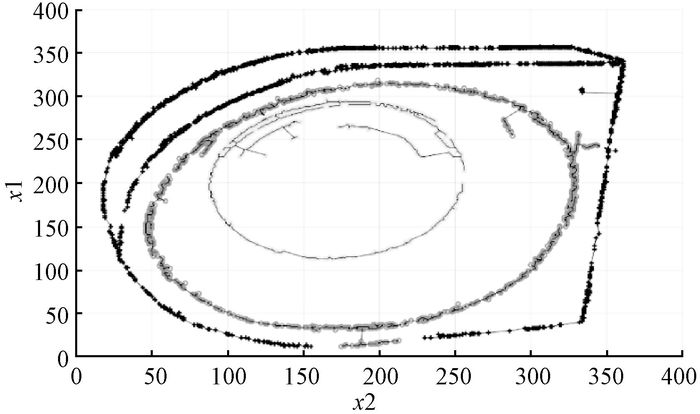
通过调节参数p,算法能够对不平衡数据实现很好的聚类效果,如图 9所示.此外,对于存在较好几何形状的数据,算法也有很好的聚类效果.如图 10和图 11所示,算法能对数据实现比较好的聚类.因此,本文提出的算法具有非常好的性能,能聚类任意形状的簇,具有较好的鲁棒性,通过调节参数可以对不平衡数据实现较好的聚类,对具有较好几何形状的数据也有非常好的效果.
|
图 9 算法在不平衡数据集上的实验 Figure 9 Experiment of the algorithm on the imbalanced data set |
|
图 10 2C数据集聚类结果 Figure 10 Clustering results of 2C data set |
|
图 11 4B数据集聚类结果 Figure 11 Clustering results of 4B data set |
真实数据集更能检验算法的性能.选用UCI数据集和Olivetti人脸数据库来验证本文算法的性能.选用的数据集从样本规模、特征个数和类簇数目都有较大差别.
3.2.1 UCI数据集实验结果分析采用ACC、AMI和ARI评价指标来验证所提出算法的性能,并与其他算法进行比较.实验结果如表 3~表 5所示.其中由于Waveform和Waveform(noise)本身数据量较大并且属性较多,有些算法没有得到聚类结果,在表中用符号“-”表示.每个数据集实验结果的最大值都进行了加黑标注.早期的K-means算法相对其他算法较稳定,善于发现球状簇.其他近期的代表性算法如DPC和AP,在个别数据集上的表现较差,但总体表现要优于其他早期算法.通过对比可以发现,在ACC评价指标下,本文提出的算法具有明显优势.在AMI和ARI评价指标下,本文提出的算法在更多的数据集上取得最大值.聚类结果表明,本文提出的算法具有非常好的性能,具有较强鲁棒性,总体聚类性能优于其他对比算法.
|
|
表 3 真实数据集上的ACC评价指标比较 Table 3 Comparison of ACC evaluation indexes on real data sets |
|
|
表 4 真实数据集上的AMI评价指标比较 Table 4 Comparison of AMI evaluation indexes on real data sets |
|
|
表 5 真实数据集上的ARI评价指标比较 Table 5 Comparison of ARI evaluation indexes on real data sets |
Olivetti人脸数据库是机器学习领域广泛使用的数据库,包含40个人的人脸图像,每个人的人脸图像是10幅不同角度的图像.由于人数(类簇数)比每个人的人脸图像数(簇内样本数)多,给聚类算法带来很大挑战.
使用本文提出的算法对Olivetti数据集进行聚类,图 12展示了本文算法的聚类结果.其中图 12(a)为人脸数据集原图像,每行2个簇,共10行.图 12(b)为聚类识别结果,对其中聚类识别错误的人脸图像加了横向阴影,并在左上角留白部分标注了“×”.ACC、AMI和ARI的值分别可以达到0.818、0.830和0.728.比较优秀的算法如DPC,只能发现20个密度峰值点,即最多能够完全聚类识别20组人脸.本文提出的算法可以聚类识别35组人脸(一组中正确标签超过半数).对于未能识别的人脸,经过对比发现,同一簇内的图像本身就存在较大差异,仅仅基于距离的度量很难准确识别,可通过特征提取的方式进一步提高准确率.

|
图 12 Olivetti数据集聚类结果 Figure 12 Clustering results of Olivetti data set |
基于互近邻距离提出了互近邻相对距离,为距离的计算提供了一种新的非度量距离计算方式.基于互近邻相对距离,提出了一种新的最小生成树聚类算法.针对某些数据的不平衡问题,提出了兼容不平衡数据的最小生成树分割方法.算法设计简单,易于实现.经典人工数据集、UCI真实数据集以及Olivetti数据集的实验结果表明,算法能够聚类任意形状的簇和兼容处理不均衡数据,通过调节参数可以实现不同的聚类效果.如果数据本身有非常好的几何形状,算法能够达到非常好的聚类效果.算法性能良好,具有较强鲁棒性,总体聚类性能优于其他对比算法.如何使本文提出的算法适用于大数据,是需要进一步研究的问题.
| [1] |
孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48-61. (  0) 0) |
| [2] |
刘志勇, 邓贵仕. 一种基于矩阵变换的层次聚类算法[J]. 郑州大学学报(理学版), 2010, 42(2): 39-42. (  0) 0) |
| [3] |
JAIN A K. Data clustering: 50 years beyond K-means[J]. Pattern recognition letters, 2010, 31(8): 651-666. DOI:10.1016/j.patrec.2009.09.011 (  0) 0) |
| [4] |
HAN J W, KAMBER M, PEI J. Data mining concepts and techniques[M]. 3rd ed. San Francisco: Morgan Kaufmann Publishers, 2012.
(  0) 0) |
| [5] |
LLOYD S P. Least squares quantization in PCM[J]. IEEE transactions on information theory, 1982, 28(2): 129-137. DOI:10.1109/TIT.1982.1056489 (  0) 0) |
| [6] |
KAUFMAN L, ROUSSEEUW P J. Finding groups in data: an introduction to cluster analysis[M]. Hoboken: John Wiley, 1990.
(  0) 0) |
| [7] |
KARYPIS G, HAN E H, KUMAR V. CHAMELEON: a hierarchical clustering algorithm using dynamic modeling[J]. Computer, 1999, 32(8): 68-75. DOI:10.1109/2.781637 (  0) 0) |
| [8] |
ZHANG T, RAMAKRISHNAN R, LIVNY M. BIRCH: an efficient data clustering method for very large databases[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data. Montreal, 1996:103-114.
(  0) 0) |
| [9] |
ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Oregon, 1996:22-69.
(  0) 0) |
| [10] |
ANKERST M, BREUNIG M M, KRIEGEL H P, et al. OPTICS: ordering points to identify the clustering structure[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data. Philadelphia, 1999:49-60.
(  0) 0) |
| [11] |
WANG W, YANG J, MUNTZ R R. STING: a statistical information grid approach to spatial data mining[C]//Proceedings of the 23rd International Conference on Very Large Data Bases. San Francisco, 1997:186-195.
(  0) 0) |
| [12] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 (  0) 0) |
| [13] |
XIE J, GAO H, XIE W, et al. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors[J]. Information sciences, 2016, 354: 19-40. DOI:10.1016/j.ins.2016.03.011 (  0) 0) |
| [14] |
谢娟英, 高红超, 谢维信. K近邻优化的密度峰值快速搜索聚类算法[J]. 中国科学(信息科学), 2016, 46(2): 258-280. (  0) 0) |
| [15] |
FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976. DOI:10.1126/science.1136800 (  0) 0) |
| [16] |
FAN J, NIU Z, LIANG Y, et al. Probability model selection and parameter evolutionary estimation for clustering imbalanced data without sampling[J]. Neurocomputing, 2016, 211: 172-181. DOI:10.1016/j.neucom.2015.10.140 (  0) 0) |
| [17] |
ZAHN C T. Graph-theoretical methods for detecting and describing gestalt clusters[J]. IEEE transactions on computers, 1971, 20(1): 68-86. (  0) 0) |
| [18] |
ZHONG C, MIAO D, WANG R. A graph-theoretical clustering method based on two rounds of minimum spanning trees[J]. Pattern recognition, 2010, 43(3): 752-766. DOI:10.1016/j.patcog.2009.07.010 (  0) 0) |
| [19] |
ZHONG C, MIAO D, FRÄNTI P. Minimum spanning tree based split-and-merge: a hierarchical clustering method[J]. Information sciences, 2011, 181(16): 3397-3410. DOI:10.1016/j.ins.2011.04.013 (  0) 0) |
| [20] |
GOWDA K C, KRISHNA G. Agglomerative clustering using the concept of mutual nearest neighbourhood[J]. Pattern recognition, 1978, 10(2): 105-112. DOI:10.1016/0031-3203(78)90018-3 (  0) 0) |
| [21] |
GOWDA K C, DIDAY E. Symbolic clustering using a new similarity measure[J]. IEEE transactions on systems man & cybernetics, 1991, 22(2): 368-378. (  0) 0) |
| [22] |
PREPARATA F P, SHAMOS M I. Computational geometry[M]. Berlin: Springer-Verlag, 1985.
(  0) 0) |
| [23] |
HELD M, KARP R M. The traveling-salesman problem and minimum spanning trees[J]. Mathematical programming, 1971, 1(1): 6-25. DOI:10.1007/BF01584070 (  0) 0) |
| [24] |
WILLETT P. Recent trends in hierarchic document clustering: a critical review[J]. Information processing & management, 1988, 24(5): 577-597. (  0) 0) |
| [25] |
EISEN M B, SPELLMAN P T, BROWN P O, et al. Cluster analysis and display of genome-wide expression patterns[J]. Proceedings of the national academy of sciences, 1998, 95(25): 14863-14868. DOI:10.1073/pnas.95.25.14863 (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


