2. 河北科技大学 理学院 河北 石家庄 050018
2. School of Sciences, Hebei University of Science and Technology, Shijiazhuang 050018, China
粗糙集[1]是一种刻画不完整性和不确定性的数学工具, 主要思想是利用已知知识库来刻画不确定或不精确的知识,被广泛应用于专家系统、图像处理、模式识别、决策分析和风险评估等领域。
经典的粗糙集方法有一定的局限性, 在处理实值信息系统时, 往往需要将数据离散化, 这可能导致一些信息的丢失。为了解决这个问题, 文献[2]提出了模糊粗糙集, 用来解决数据集中存在的不确定性和模糊性, 将模糊集与粗糙集结合, 给出了实值数据不确定性推理的关键方法。文献[3]提出了直觉模糊集, 考虑到了隶属度、非隶属度与犹豫度, 可以更好地处理不确定性, 具有更强的处理信息系统的能力。考虑到其只能描述隶属度与非隶属度小于和等于1的情况, 文献[4]提出了毕达哥拉斯模糊集, 要求隶属度与非隶属度的平方和小于等于1即可, 可行域为半径为1的1/4圆域, 是非常有现实意义的。目前, 毕达哥拉斯模糊集主要应用于多准则(属性)决策中[5-6]。属性约简是粗糙集理论研究的核心内容之一, 它是在保持知识库分类能力不变的条件下, 删除其中不相关或不重要的属性。文献[7]提出的辨识矩阵是求最小约简的有力工具。文献[8]提出了基于辨识矩阵的属性集求核算法, 减少了对象之间不必要的比较以及矩阵中的空值存储。文献[9]提出将形式背景中的属性约简与图论相结合, 将形式背景的属性约简问题转化为图论中的最小顶点覆盖问题, 并证明这种方法大大减少了算法的时间复杂度。因此我们考虑将辨识矩阵和最小顶点覆盖应用到Pythagorean模糊信息系统的属性约简中。
本文定义了Pythagorean模糊信息系统中的辨识矩阵, 将辨识矩阵的布尔推理问题转化为图论中的最小顶点覆盖问题, 给出了属性约简的算法, 并通过实例表明该算法的有效性, 最后定义了Pythagorean模糊决策信息系统中的属性约简算法, 用实例证明算法的可行性, 并进行了对比分析。
1 基础概念 1.1 基于加权欧几里得距离的相似度相似度的定义有很多种方法, 应用比较广泛的是文献[10]提出的模糊相似关系。
定义1[10] 若F=(U, A, I, f)为一个模糊信息系统, U为对象集, A为属性集, I为所有模糊集的集合, f:U×A→I为映射, ∀a∈A, 相似度定义为sima(xi, xj)=1-|μa(xi)-μa(xj)|/|μamax-μamin|,其中:μa(xi)、μa(xj)分别为对象xi、xj对于属性a的隶属度;μamax、μamin分别为所有对象对于属性a的最大和最小隶属度。文献[11]定义了直觉模糊信息系统基于加权欧几里得距离的相似关系。
定义2[11] 若F=(U, A, I, f)为直觉模糊信息系统, U为对象集, A为属性集, I为所有直觉模糊集的集合, f:U×A→I为映射, ∀xi, xj∈U, a∈A, 两个直觉模糊集分别为f(xi, a)=〈μa(xi), νa(xi)〉和f(xj, a)=〈μa(xj), νa(xj)〉,基于加权欧几里得距离的相似度定义为
| $ \mathit{si}{\mathit{m}_a}\left( {{x_i}, {x_j}} \right) = 1 - \sqrt {\alpha {{\left| {{\mu _a}\left( {{x_i}} \right) - {\mu _a}\left( {{x_j}} \right)} \right|}^2} + \beta {{\left| {{\nu _a}\left( {{x_i}} \right) - {\nu _a}\left( {{x_j}} \right)} \right|}^2} + \gamma {{\left| {{\pi _a}\left( {{x_i}} \right) - {\pi _a}\left( {{x_j}} \right)} \right|}^2}} , $ |
其中α、β、γ为加权因子。
1.2 Pythagorean模糊信息系统定义3[12-13] 设U为给定的非空论域, 集合X={〈x, μX(x), νX(x)〉|x∈U}称为Pythagorean模糊集, 若满足0≤μX2(x)+νX2(x)≤1, μX(x), νX(x)∈[0, 1], 其中μX(x)表示元素x对于集合X的隶属度, νX(x)表示元素x对于集合X的非隶属度, ${\pi _X}(x) = \sqrt {1 - \mu _X^2(x) - \nu _X^2(x)} $称为元素x对于集合X的犹豫度。λ=〈μX(x), νX(x)〉为Pythagorean模糊数。
定义4[12-13] 设四元组S=(U, A, VPF, f)表示一个Pythagorean模糊信息系统, U={x1, x2, …, xn}为对象的集合, A={a1, a2, …, am}为属性集合, VPF为所有的Pythagorean模糊集的集合, f:U×A→VPF为映射, 对任意的x∈U和a∈A, 有f(x, a)=〈μa(x), νa(x)〉, 其中:μa(x)为对象x关于属性a的隶属度;νa(x)为对象x关于属性a的非隶属度, 且满足0≤μX2(x)+νX2(x)≤1, μX(x), νX(x)∈[0, 1]。
1.3 辨识矩阵的简化当数据维数较大时, 辨识矩阵中逻辑运算的计算量较大, 需要对辨识矩阵进行简化。
定义5[14] (1) ∀(x, y)∈U×U, M(x, y)≠Ø⇒MS(x, y)≠Ø, 且MS(x, y)⊆M(x, y); (2) ∀(x, y)∈U×U, M(x, y)=Ø⇒MS(x, y)=Ø。倘若满足以上两个条件时,矩阵MS称为辨识矩阵M的简化辨识矩阵。
元素吸收[14]指若矩阵中一元素M(x′, y′)≠Ø, 满足M(x, y):Ø≠M(x′, y′)⊂M(x, y)。此矩阵中M(x, y)的值被M(x′, y′)代替。
矩阵吸收[14]:矩阵吸收运算的规则是, 在满足Ø≠M(x′, y′)⊂M(x, y)的情况下, 对矩阵中所有可能的元素对都进行吸收操作。简化后的辨识矩阵得到的约简与原辨识矩阵得到的约简相同。
2 Pythagorean模糊信息系统的图表示对于一些维数较大的数据集来说, 辨识矩阵的析取与合取的算法过程复杂度较大, 考虑将辨识矩阵的约简转化为图的最小顶点覆盖来简化计算量。首先定义Pythagorean模糊信息系统中基于加权欧几里得距离的相似度和辨识矩阵。
2.1 Pythagorean模糊信息系统中的加权欧几里得距离及相似关系由于Pythagorean模糊信息系统是直觉模糊信息系统的推广,因此将直觉模糊集的一些性质推广到Pythagorean模糊集中。首先给出Pythagorean模糊信息系统中的相似关系并讨论它的性质。
定义6 设λ1=〈μ1, ν1〉与λ2=〈μ2, ν2〉为两个Pythagorean模糊数, 则D(λ1, λ2)=$\sqrt {\alpha {{\left| {\mu _1^2 - \mu _2^2} \right|}^2} + \beta {{\left| {\nu _1^2 - \nu _2^2} \right|}^2} + \gamma {{\left| {\pi _1^2 - \pi _2^2} \right|}^2}} $称为Pythagorean模糊数的加权欧几里得距离, 其中α、β、γ为加权因子, 本文中规定加权因子α、β、γ满足条件:(1) 0≤α, β, γ≤1, 其中α, β≠0;(2) α+β+γ=1;(3) α≥β>γ。
性质1 设λ1=〈μ1, ν1〉, λ2=〈μ2, ν2〉, λ3=〈μ3, ν3〉为3个Pythagorean模糊数, 则D(λi, λj)为一个度量, 其中i, j=1, 2, 3。对于任意的Pythagorean模糊数λ1、λ2、λ3, 则(1) D(λ1, λ2)≥0, 且D(λ1, λ2)=0,当且仅当λ1=λ2; (2) D(λ1, λ2)=D(λ2, λ1); (3) D(λ1, λ2)≤D(λ1, λ3)+D(λ3, λ2)。
下面定义Pythagorean模糊信息系统中两个对象的相似度。
定义7 设S=(U, A, VPF, f)为Pythagorean模糊信息系统, 若(xi, xj)∈U, ak∈A, f(xi, ak)=〈μak(xi), νak(xi)〉与f(xj, ak)=〈μak(xj), νak(xj)〉为两个Pythagorean模糊数, α、β、γ为加权因子。关于ak的基于加权欧几里得距离的相似度sim定义为
| $ \mathit{si}{\mathit{m}_{{a_k}}}\left( {{x_i}, {x_j}} \right) = 1 - \sqrt {\alpha {{\left| {\mu _{{a_k}}^2\left( {{x_i}} \right) - \mu _{{a_k}}^2\left( {{x_j}} \right)} \right|}^2} + \beta {{\left| {\nu _{{a_k}}^2\left( {{x_i}} \right) - \nu _{{a_k}}^2\left( {{x_j}} \right)} \right|}^2} + \gamma {{\left| {\pi _{{a_k}}^2\left( {{x_i}} \right) - \pi _{{a_k}}^2\left( {{x_j}} \right)} \right|}^2}} 。$ |
性质2 设S=(U, A, VPF, f)为Pythagorean模糊信息系统, 对于任意xi, xj∈U, ak∈A, 关于ak的基于加权欧几里得距离的相似度满足性质:(1) 0≤simak(xi, xj)≤1;(2) simak(xi, xj)=simak(xj, xi); (3) f(xi, ak)=f(xj, ak)⇔simak(xi, xj)=1;(4)若f(xi, ak)=〈1, 0〉, f(xj, ak)=〈0, 1〉, 且α+β=1, 则simak(xi, xj)=0, 也就是说, xi和xj在性质ak上的表现完全不同。
定义8 设S=(U, A, VPF, f)为Pythagorean模糊信息系统, 对于任意ak∈A, δ∈[0, 1], 两个对象的δ-相似关系定义为Rδ(A)={(xi, xj)∈U×U|simak(xi, xj)≥δ, ∀ak∈A}。
性质3 设S=(U, A, VPF, f)为Pythagorean模糊信息系统, Rδ(A)为由属性A决定的二元关系, 则以下性质成立:(1)对任意xi∈U, Rδ(A)(xi, xi)=1;(2)对任意xi, xj∈U, Rδ(A)(xi, xj)=Rδ(A)(xj, xi)。对任意的C⊆A, δ∈[0, 1], 有Rδ(C)=∩ck∈CRδ(ck), 且Rδ(A)⊆Rδ(C)。
参数δ往往根据数据集的分布特征进行取值, 不同的δ代表对象xi与xj之间不同的相似度和信息系统中不同的相似关系。当数据集的相似程度较大时, 应选择更大的δ值, 反之亦然。
定义9 若S=(U, A, VPF, f)为Pythagorean模糊信息系统, δ∈[0, 1], Rδ(A)为由属性集A决定的二元关系, C⊆A, 称C为属性集A的约简(记为red(A)), 满足条件:(1) Rδ(A)=Rδ(C); (2)对任意元素c∈C, Rδ(A)≠Rδ(C-{c})。
2.2 基于相似关系的辨识矩阵为了得到Pythagorean模糊信息系统的属性约简, 引入基于相似关系的辨识矩阵。
定义10 设S=(U, A, VPF, f)为Pythagorean模糊信息系统。记MS(x, y)={ak∈A:simak(x, y) < δ}为x与y的辨识属性集, 其中(x, y)∈U×U, 称矩阵MS=MS(x, y)为信息系统S的辨识矩阵。
定义11 设S=(U, A, VPF, f)为Pythagorean模糊信息系统, (x, y)∈U×U。MS=MS(x, y)为信息系统S的辨识矩阵, 其中MS(x, y)为x与y的辨识属性集。设辨识函数fS为含有m个分别与属性a1, a2, …, am对应的布尔变量a1*, a2*, …, am*的布尔函数[6], 定义为fS(a1*, a2*, …, am*)=∧{∨MS(x, y):MS(x, y)∈MS}=∨(∧red),其中∨MS(x, y)为MS(x, y)中所有属性的析取, 即对象x与y可以被M(x, y)中任意一个属性区分, 则red为约简。
例1 设S=(U, A, VPF, f)为一个Pythagorean模糊信息系统, 其中:U={x1, x2, x3, x4}为4个病人的集合; AT={a1, a2, a3, a4}为4个属性的集合, a1:=heat, a2:=cough, a3:=headache, a4:=sorethroat, 信息如表 1所示, 令δ=0.8, α=0.4, β=0.4, γ=0.2。
| $ {\mathit{\boldsymbol{M}}_s} = \left( {\begin{array}{*{20}{c}} \emptyset &{}&{}&{}\\ {\left\{ {{a_1}, {a_2}, {a_3}} \right\}}&\emptyset &{}&{}\\ {\left\{ {{a_3}} \right\}}&A&\emptyset &{}\\ A&{\left\{ {{a_1}, {a_4}} \right\}}&{\left\{ {{a_3}, {a_4}} \right\}}&\emptyset \end{array}} \right), $ |
|
|
表 1 4个病人的信息表 Tab. 1 An information table of four patients |
根据两对象相似度的定义可得sima1(x1, x2)=0.505, sima2(x1, x2)=0.714, sima3(x1, x2)=0.518, sima4(x1, x2)=0.916, M(x1, x2)={ak∈A:sim(x1, x2) < 0.8}={a1, a2, a3}。同理可计算M(x1, x3)={a3}, M(x1, x4)=A, M(x2, x3)=A, M(x2, x4)={a1, a4}, M(x3, x4)={a3, a4}。进而得到辨识矩阵MS为red(A)=(a1∨a2∨a3)∧(a1∨a2∨a3∨a4)∧a3∧(a1∨a4)∧(a3∨a4)=(a3∧a1)∨(a3∧a4), 即得到两个约简集{a1, a3}和{a3, a4}。任何一个约简集都含有的元素称为核心元素, 记为core(A), 即core(A)=∩red(A)。例1中core(A)={a3}。
定理1 若S=(U, A, VPF, f)为一个Pythagorean模糊信息系统, C⊆A, δ∈[0, 1], MS为此信息系统的辨识矩阵, 则有core(A)={a∈A:M(x, y)={a}}。
即核心属性为辨识矩阵中所有单个元素的集合。
2.3 辨识矩阵的图表示方法下面我们将辨识矩阵的约简与图中最小顶点覆盖联系起来。
定义12[9, 15] 给定一个图G=〈V, E〉, 且e∈E, 令N(e)为连接边e的一个顶点集。定义N={N(e):e∈E}。设fG为图G的一个布尔函数, 由m个布尔变量v0*, v1*, …, vm*构成, 且布尔变量与顶点集v0, v1, …, vm一一对应。fG(v1*, v2*, …, vm*)=∧{∨N(e):N(e)∈N},其中∨N(e)为所有布尔变量v*的析取, v∈N(e)。由此可见, 图的最小顶点覆盖也可通过布尔公式得到。
定理2[9] 设G=〈V, E〉为一个图, 顶点集K⊆V是图G的最小顶点覆盖,当且仅当∧vi∈Kvi*是布尔函数fG极小析取范式中的合取式。
若将布尔函数fG化简, 则布尔函数fG(v1*, v2*, …, vm*)=∧{∨N(e):N(e)∈N}=∨i=1t(∧j=1sivj*), 其中∧j=isivj*, i≤t为布尔函数fG的极小析取范式中的所有合取式, 而Ki={vj:j≤si}, i≤t, 为图G的所有最小顶点覆盖[9]。在后面的讨论中, 用vi来代替vi*。
定义13 设MS为Pythagorean模糊信息系统S=(U, A, VPF, f)的辨识矩阵, 令V=A, E={e∈MS:e≠Ø}, 称GS=〈V, E〉为Pythagorean模糊信息系统S的生成图。
|
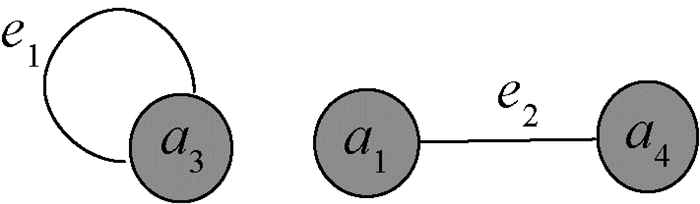
图 1 由S生成的图GS Fig. 1 Graph GS induced from S |
例2 以例1中的简化后的辨识矩阵为例。生成图中顶点集为V={a1, a3, a4}, 边集E={e1, e2}, 如图 1所示, e1与a3关联, e2与a1和a4关联, 关联矩阵用MG表示。
定理3 设GS=〈V, E〉为由Pythagorean模糊信息系统S=(U, A, VPF, f)的辨识矩阵生成的图, red(S)为Pythagorean模糊信息系统S的约简, v(GS)为S产生的图GS的最小顶点覆盖, 则v(GS)=red(S)。
性质4 若S=(U, A, VPF, f)为Pythagorean模糊信息系统, δ∈[0, 1], Rδ(A)为由属性集A决定的二元关系, MS为辨识矩阵, 若MS中元素MS(x, y)由A中的单个元素a组成, 那么在生成图中, a为一个含有环的顶点。
2.4 基于相似度的属性约简算法(算法1)输入:Pythagorean模糊信息系统S=(U, A, VPF, f), δ, 加权因子α, β, γ。
输出:S的约简red(A)。
1.根据相似关系的定义计算辨识矩阵MS并简化。/*删掉重复行, 满行及零行*/
2.找到所有含有环的顶点, 这些顶点构成的集合定义为red。
3.对任意顶点v∈red, 删除所有与顶点v关联的边。/*删除关联矩阵MG中的某些行*/
4. While MG≠Ø do
5.找度最大的顶点v0, 令red=red∪{v0}。
6.删除所有与顶点v0相关联的边。
7. End while
8.对任意v∈red, 若与顶点v关联的边都被点集red-{v}覆盖, 则删除顶点v。
9.返回red。
此算法在最坏情况下的时间复杂度为O(|U|(|U|-1)|A|+|U|(|U|-1)/2+2|A|+|U|), 为多项式时间复杂度, 可记为O(U2A), 经过简化矩阵之后, 矩阵运算的维度降低, 使算法的效率更高。
2.5 实例分析为了验证基于图论的Pythagorean模糊信息系统的属性约简算法的可行性和有效性, 在目前已有的Pythagorean模糊集数据上, 进行排列组合得到较大规模数据集,如表 2所示。数据集中含有50个对象, 7个条件属性和4个决策属性。data1、data2、data3分别由数据集中的前10、20、50个对象以及条件属性构成。用不同的数据集, 不同的约简方法以及不同的参数得到的约简结果及约简时间见表 3和表 4。表 3中α、β、γ分别为0.4、0.4、0.2, 在表 4中分别为0.5、0.4、0.1。通过对比可见, 随着参数δ的增大, 得到的约简基数变小。本文的算法得到的约简包含在原始算法得到的约简中, 且在一定条件下等于原始算法的最小约简, 原始算法可得到所有可能的约简结果,但是图论方法可以节省算法的时间。
|
|
表 2 数据集 Tab. 2 Data sets |
|
|
表 3 不同数据集的约简结果及约简时间对比 Tab. 3 Comparison of reduction results and reduction time for different data sets |
|
|
表 4 不同数据集的约简结果及约简时间对比 Tab. 4 Comparison of reduction results and reduction time for different data sets |
在约简的过程中, 若出现度数相同的顶点(条件属性), 总是优先考虑角标较小的点, 在实际应用中可根据决策者的偏好, 优先选择相对重要的属性。
3 Pythagorean模糊决策信息系统约简的图解法 3.1 Pythagorean模糊决策信息系统的辨识矩阵定义14 Pythagorean模糊决策信息系统是一个五元组F=(U, A, V, D, I), A为条件属性集, D为决策属性集, δ∈[0, 1], 则Pythagorean模糊决策信息系统中的δ-相似关系Rδ(A|D)定义为
| $ {R^\delta }(A|D) = \left\{ {\left( {{x_i}, {x_j}} \right) \in U \times U|\forall {a_k} \in A, {{{\mathop{\rm sim}\nolimits} }_{{a_k}}}\left( {{x_i}, {x_j}} \right) \ge \delta \vee {I_D}\left( {{x_i}} \right) = {I_D}\left( {{x_j}} \right)} \right\}。$ |
定义15 令F=(U, A, V, D, I)为Pythagorean模糊决策信息系统, δ∈[0, 1], C⊆A为属性集A关于D的一个约简, 满足条件:(1)Rδ(CD)=Rδ(AD); (2)∀C′⊂C, Rδ(C′D)≠Rδ(AD)。
定义16 令F=(U, A, V, D, I)为Pythagorean模糊决策信息系统, (x, y)∈U×U, 则称
| $ {\mathit{\boldsymbol{M}}_F}(x, y) = \left\{ {\begin{array}{*{20}{l}} {\left\{ {{a_k} \in A;\mathit{si}{\mathit{m}_{{a_k}}}(x, y) < \delta } \right\}, }&{{I_D}(x) \ne {I_D}(y), }\\ {\emptyset , }&{{\rm{ otherwise}}{\rm{。}}} \end{array}} \right. $ |
为F中x与y的辨识属性集, 称MF={MF(x, y):(x, y)∈U×U}为F的辨识矩阵, 辨识函数类似地定义为fF(a1, a2, …, am)=∧{∨MF(x, y):MF(x, y)∈MF, MF(x, y)≠Ø}。
3.2 辨识矩阵的图表示定义17 令F=(U, A, V, D, I)为Pythagorean模糊决策信息系统, MF为辨识矩阵, GF=〈V, E〉称为Pythagorean模糊决策信息系统的生成图, 若V=A, E={e∈MF, e≠Ø}。
通过定理2中信息系统的约简与生成图中顶点覆盖的关系, 可以得到关于Pythagorean模糊决策信息系统的相关结论。
定理4 若GF=〈V, E〉为Pythagorean模糊决策信息系统F=(U, A, V, D, I)的生成图, 则有red(F)=v(GF)。
以上结果对于超图依然成立。
例3 表 5为一个Pythagorean模糊决策信息系统F=(U, A, V, D, I), 其中:U={x1, x2, x3, x4};A={a1, a2, a3, a4};D={d}。令δ=0.7, α=0.4, β=0.4, γ=0.2。
|
|
表 5 Pythagorean模糊决策信息系统决策表 Tab. 5 Decision table of pythagorean fuzzy decision information system |
根据定义10, 利用辨识函数得到约简{a1, a3}, {a1, a4}, {a3, a4}, {a2, a4}。通过辨识矩阵可得生成图GF=〈V, E〉, 关联矩阵如表 6所示。得到辨识矩阵MS为
| $ {\mathit{\boldsymbol{M}}_s} = \left( {\begin{array}{*{20}{c}} \emptyset &{}&{}&{}\\ {\left\{ {{a_1}, {a_2}, {a_3}} \right\}}&\emptyset &{}&{}\\ \emptyset &A&\emptyset &{}\\ A&{\left\{ {{a_1}, {a_4}} \right\}}&{\left\{ {{a_3}, {a_4}} \right\}}&{\emptyset )} \end{array}} \right), $ |
|
|
表 6 关联矩阵MG Tab. 6 Incidence matrix MG |
生成图GF=〈V, E〉中, V={a1, a2, a3, a4}, E={{a1, a2, a3}, {a1, a4}, {a3, a4}}, 显然red(F)=v(GF)={{a1, a4}, {a1, a3}, {a2, a4}, {a3, a4}}。
性质5 令F=(U, A, V, D, I)为Pythagorean模糊决策信息系统, 称SF(U, A, V)为由F生成的Pythagorean模糊信息系统, MS为SF的辨识矩阵, MF为F的辨识矩阵, 对任意x, y∈U, 可得关系
| $ {\mathit{\boldsymbol{M}}_F}(x, y) = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{M}}_s}(x, y), }&{{I_D}(x) \ne {I_D}(y);}\\ {\emptyset , }&{{\rm{ otherwise}}{\rm{。}}} \end{array}} \right. $ |
根据定义10和16可证上式成立,由此可见, 对任意x, y∈U, 恒有MF(x, y)=MS(x, y)。
3.3 Pythagorean模糊决策信息系统的属性约简算法(算法2)输入:Pythagorean模糊决策信息系统F=(U, A, V, D, I), δ, 加权因子α, β, γ。
输出:F的约简red(A)。
1.根据算法1, 找到Pythagorean模糊信息系统SF(U, A, V)生成图的辨识矩阵MS。
2. if ID(x)=ID(y)
3. MF(x, y)=MS(x, y)
4. else MF(x, y)=Ø
5.产生图的关联矩阵MG。
6.利用算法1中步骤3~9, 得到约简red(A)。
3.4 实验分析选取表 2中的前10、20、50个数据以及对应的条件和决策属性作为data4、data5、data6。算法的约简结果及运行时间见表 7(参数α、β、γ分别为0.4、0.4、0.2)和表 8(参数α、β、γ分别为0.5、0.4、0.1)。可见在约简结果相同的条件下,本文提出的算法大大减少了算法复杂度。
|
|
表 7 不同数据集的约简结果及约简时间对比 Tab. 7 Comparison of reduction results and reduction time for different data sets |
|
|
表 8 不同数据集的约简结果及约简时间对比 Tab. 8 Comparison of reduction results and reduction time for different data sets |
本文主要讨论了Pythagorean模糊信息系统和Pythagorean模糊决策信息系统中的属性约简问题。利用加权欧几里得距离定义了对象之间的相似度, 然后利用信息系统中的约简与图论中顶点覆盖之间的关系, 将辨识矩阵转化为图论中的关联矩阵, 将NP-Hard问题简化为多项式复杂度的问题, 减少了约简算法的时间复杂度, 给出了Pythagorean模糊信息系统和Pythagorean模糊决策信息系统中属性约简的算法, 最后分别用实例验证了其可行性, 并进行了对比分析。
| [1] |
PAWLAK Z. Rough sets[J]. International journal of computer and information sciences, 1982, 11(5): 341-356. DOI:10.1007/BF01001956 (  0) 0) |
| [2] |
DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. International journal of general systems, 1990, 17(2/3): 191-209. (  0) 0) |
| [3] |
ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy sets and systems, 1986, 20(1): 87-96. (  0) 0) |
| [4] |
YAGER R R. Pythagorean membership grades in multicriteria decision making[J]. IEEE transactions on fuzzy systems, 2014, 22(4): 958-965. DOI:10.1109/TFUZZ.2013.2278989 (  0) 0) |
| [5] |
ZENG S Z, CHEN J P, LI X S. A hybrid method for Pythagorean fuzzy multiple-criteria decision making[J]. International journal of information technology & decision making, 2016, 15(2): 403-422. (  0) 0) |
| [6] |
REN P J, XU Z S, GOU X J. Pythagorean fuzzy TODIM approach to multi-criteria decision making[J]. Applied soft computing, 2016, 42: 246-259. DOI:10.1016/j.asoc.2015.12.020 (  0) 0) |
| [7] |
SKOWRON A, RAUSZER C. The discernibility matrices and functions in information systems[M]. Dordrecht: Springer Netherlands, 1992: 331-362.
(  0) 0) |
| [8] |
杨涛, 张贤勇, 冯山. 基于差别矩阵的属性集求核算法[J]. 郑州大学学报(理学版), 2018, 50(1): 27-32. YANG T, ZHANG X Y, FENG S. A core algorithm of attribute sets based on the discernibility matrix[J]. Journal of Zhengzhou university(natural science edition), 2018, 50(1): 27-32. (  0) 0) |
| [9] |
CHEN J K, MI J S, LIN Y J. A graph approach for knowledge reduction in formal contexts[J]. Knowledge-based systems, 2018, 148: 177-188. DOI:10.1016/j.knosys.2018.02.039 (  0) 0) |
| [10] |
JENSEN R, SHEN Q. Computational intelligence and feature selection: rough and fuzzy approaches[J]. Kybernetes, 2009, 38: 3-4. (  0) 0) |
| [11] |
FENG Q R, LI R. Discernibility matrix based attribute reduction in intuitionistic fuzzy decision systems[M]. Berlin: Springer, 2013: 147-156.
(  0) 0) |
| [12] |
YAGER R R. Pythagorean membership grades in multicriteria decision making[J]. IEEE transactions on fuzzy systems, 2014, 22(4): 958-965. DOI:10.1109/TFUZZ.2013.2278989 (  0) 0) |
| [13] |
QU G H, ZHANG H P, LIU Z L. Group decision making based on λ-shapley Choquet integral novel intuitionistic fuzzy TOPSIS method[J]. System engineering theory and practice, 2016, 36(3): 726-742. (  0) 0) |
| [14] |
YAO Y Y, ZHAO Y. Discernibility matrix simplification for constructing attribute reducts[J]. Information sciences, 2009, 179(7): 867-882. DOI:10.1016/j.ins.2008.11.020 (  0) 0) |
| [15] |
左孝凌, 李为鑑, 刘永才. 离散数学[M]. 上海: 上海科学技术文献出版社, 1988. ZUO X L, LI W J, LIU Y C. Discrete mathematics[M]. Shanghai: Shanghai Science and Technology Literature Publishing Press, 1988. (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


