多数隐写算法在嵌入数据后会造成原始载体的永久性失真,这在一些对数据认证要求较高的领域里是不允许的,例如云环境下的隐私保护、军事作战地图传输等[1].而可逆信息隐藏技术(reversible data hiding,RDH)克服了这一缺点,其中基于密文域可逆信息隐藏(reversible data hiding in encrypted domain,RDH-ED)越来越得到人们的重视[2-4].传统的RDH-ED算法基于流加密,通过翻转像素的LSB(least significant bit)嵌入信息,并在解密后利用相邻像素的相关性提取数据和恢复原始载体[5].文献[6-7]实现秘密数据的提取和原始图像恢复的可分离,即合法的接收者可根据密钥的不同进行提取和解密操作.在满足可分离的要求下,基于像素直方图扩展的RDH-ED方法得到广泛关注,数据隐藏阶段使用伪随机密钥选择多个单独像素,通过直方图漂移嵌入秘密数据可有效提高嵌入率.文献[8]提出一种基于图像分块加密的RDH-ED新方案,适用于当前所有基于直方图漂移的可逆信息算法,但是同一个子块中每个像素利用相同的伪随机流进行异或加密,其安全性不高;文献[9]则通过对原始载体进行分块,子块内进行Josephus变换和利用子块直方图漂移隐藏数据,载体加密安全性也不高.
以上RDH-ED算法采用流加密系统进行加密,对密钥管理的难度较大,而且不能对密文信号进行处理.为解决以上问题并保证在原始图像解密后低失真的情况下,提高其嵌入容量,本文提出了一种基于Paillier同态公钥加密系统的RDH-ED方法[10].实验数据显示,标准图像库中图像嵌入数据的最大平均嵌入率为0.128 bpp,而且在直接解密情况下可以无损恢复原始图像,提取正确率达100%.
1 相关知识 1.1 Paillier同态加密系统给定2个大素数p和q,n=pq,λ =lcm(p-1,q-1),其中lcm表示求p-1和q-1的最小公倍数.取g∈Zn2*,且满足gcd(L(gλmod n2), n)=1,gcd表示求L(gλmod n2)和n的最大公约数,Zn2*表示Zn2中与n2互质的整数的集合,这里:
| $ L\left( x \right) = \frac{{x - 1}}{n}. $ |
加密公钥K1为(n, g),私钥K2为(p, q), 随机选取整数r∈ Zn*,明文m∈ Zn*,加密结果为
| $ c = {g^m}{r^n}{\rm{mod}}\;{\mathit{n}^2}, $ |
式中:c是明文m对应的密文数据,且c∈Zn2*.记加密算法为c=E(m, r),由此可知,对于相同的密文m,加密过程中随机选取的r值可能不同,其加密后对应的密文数据也不相同,从而保证了密文数据语义上的安全性.其解密过程为
| $ m = D\left( c \right) = \frac{{L({c^\lambda }{\rm{mod}}\;{n^2})}}{{L({\mathit{g}^\lambda }{\rm{mod}}\;{n^2})}}{\rm{mod}}\;\mathit{n}\mathit{.} $ |
定理1 若g的阶为n的非零整数倍,则c=E(m, r)是双射[11].即当g满足上述要求时,∀(m, r)|m∈Zn*,r∈ Zn*都有唯一的c=E(m, r)与之一一对应.
本文算法将利用定理1提取加密域中嵌入的数据.
1.2 游程编码压缩游程编码压缩(run length coding)是一种与资料性质无关的无损数据压缩技术,其原理是用一个整数对(L,R)表示一个游程序列,游程序列是指连续出现且相等的数字序列.在对图像数据进行编码时,沿一定方向排列的具有相同灰度值的像素可看成是连续符号,用字串代替这些连续符号.定长RLC是指游程序列长度R所占用的比特位数固定,RLC-u′位元表示法是定长RLC的一种无损压缩方法,即利用u′个比特位来储存整数,例如u′=8,对连续的二进制序列11111100000000000001100000进行RLC-u′位元表示法压缩,结果为6 180 502 150.本文将利用RLC-u′位元表示法压缩灰度图像的高位位平面H.
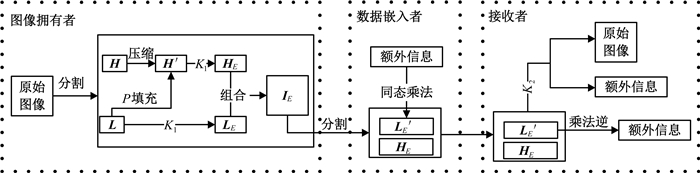
2 基于同态公钥加密系统的可逆信息隐藏算法 2.1 算法总体框架基于同态公钥加密系统的可逆信息隐藏算法框架如图 1所示.图像拥有者对原始载体进行位平面分割,把H进行RLC-u′位元表示法压缩,并根据压缩出来的冗余空间在L中选取元素D,D的坐标信息记为D_map,而后利用D_map重构高位位平面H′,再后利用公钥K1分别加密H′和低位位平面L,得到加密后的高、低位位平面HE和LE,完成加密过程,并把HE和LE进行组合,得到加密后的图像IE.数据嵌入者接收到加密载体,进行密文图像分割操作得到HE和LE,加密处理秘密数据,这里的秘密数据是嵌入的需要保密的信息.根据D_map,利用密文同态乘法把额外数据嵌入到低位位平面中,得到嵌入数据的L′E,把HE和L′E进行组合,发送给接收者.接收者执行同发送方相同的分割操作,而后利用同态乘法逆提取嵌在L′E中的秘密数据;也可直接利用私钥K2进行解密,既可以恢复原始图像,也能提取秘密数据.
|
图 1 基于同态公钥加密系统的可逆信息隐藏算法框架 Figure 1 Framework of reversible data hiding algorithm based on homomorphic public key encryption system |
设8位灰度图像I的大小为M×N,图像I的像素记为Ii, j,Ii, j可用二进制表示为{bi, j, 0,bi, j, 1,bi, j, 2,bi, j, 3,bi, j, 4,bi, j, 5,bi, j, 6,bi, j, 7},则有
| $ \begin{array}{l} {b_{i, j, k}} = \left\lfloor {\frac{{{I_{i, j}}}}{{{2^k}}}} \right\rfloor {\rm{mod}}\;2, k = 0, 1, \cdots, 7, \\ {I_{i, j}} = \sum\limits_{k = 0}^7 {{b_{i, j, k}} \times {2^{7 - k}}, 0 \le {I_{i, j}} \le 255} {\rm{, }} \end{array} $ |
其中{0≤Ii, j≤255|1≤i≤M,1≤j≤N},
| $ {\mathit{\boldsymbol{I}}_{M \times N}} = \left[{\begin{array}{*{20}{c}} {{I_{1, 1}}, {I_{1, 2}}, \cdots, {I_{1, j}}, \cdots, {I_{1, N}}}\\ \vdots \\ {{I_{i, 1}}, {I_{i, 2}}, \cdots, {I_{i, j}}, \cdots, {I_{i, N}}}\\ \vdots \\ {{I_{M, 1}}, {I_{M, 2}}, \cdots, {I_{M, j}}, \cdots, {I_{M, N}}} \end{array}} \right]. $ |
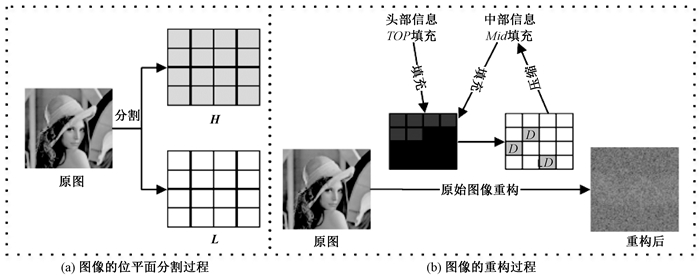
图像的位平面分割过程如图 2(a)所示,图像拥有者将I按位由高到低的顺序分解为2个不同的位平面,记前x个比特(即bi, j, 0,bi, j, 1,…,bi, j, x-1)所代表的元素组合成的高位位平面为H;记最后y个比特(即bi, j, x,bi, j, x+1,…,bi, j, 7)所代表的元素组合成的低位位平面为L,x+y=8.hi, j、li, j分别表示上2个位平面矩阵中的元素,且有hi, j∈[0, 2x-1],li, j∈[0, 2y-1],则有
| $ {l_{i, j}} = \sum\limits_{k = 0}^{x - 1} {{b_{i, j, k}} \times {2^k}, {b_{i, j, k}} \in \left\{ {0, 1} \right\}}, \;\;{h_{i, j}} = \sum\limits_{k = 0}^{7 - x} {{b_{i, j, k}} \times {2^k}, {b_{i, j, k}} \in \left\{ {0, 1} \right\}} . $ |
|
图 2 图像的位平面分割与重构过程 Figure 2 The bit-plane segmentation and reconstruction process of the image |
高位位平面H和低位位平面L可以分别表示为
| $ {\mathit{\boldsymbol{H}}_{M \times N}} = \left[{\begin{array}{*{20}{c}} {{h_{1, 1}}, {h_{1, 2}}, \cdots, {h_{1, j}}, \cdots, {h_{1, N}}}\\ \vdots \\ {{h_{i, 1}}, {h_{i, 2}}, \cdots, {h_{i, j}}, \cdots, {h_{i, N}}}\\ \vdots \\ {{h_{M, 1}}, {h_{M, 2}}, \cdots, {h_{M, j}}, \cdots, {h_{M, N}}} \end{array}} \right], \;{\mathit{\boldsymbol{L}}_{M \times N}} = \left[{\begin{array}{*{20}{c}} {{l_{1, 1}}, {l_{1, 2}}, \cdots, {l_{1, j}}, \cdots, {l_{1, N}}}\\ \vdots \\ {{l_{i, 1}}, {l_{i, 2}}, \cdots, {l_{i, j}}, \cdots, {l_{i, N}}}\\ \vdots \\ {{l_{M, 1}}, {l_{M, 2}}, \cdots, {l_{M, j}}, \cdots, {l_{M, N}}} \end{array}} \right]. $ |
图像的重构过程如图 2(b)所示,具体步骤如下.
Step 1:按从上到下、从左到右扫描H中所有元素,并把这些元素组合成一个数据串S;
Step 2:对S利用RLC-u′位元表示法游程压缩,得到压缩后的数据串S′,且S′中的整数对为(Left,Right),有Left,Right ∈[0,2u′-1],因此不会溢出;
Step 3:统计S′的长度记为LS,并用二进制表示LS,以u′位比特串为一组,重构十进制LS,重组后记为L′S;
Step 4:统计L中的元素D,记其坐标信息为D_map,利用同Step 3相同的方法处理D_map,其长度记为LD_map,此过程即是记录在L中嵌入秘密数据的位置;
Step 5:将L′S和LD_map组合成H的头部信息,记为Top(L′S,LD_map),而后把中部信息Mid(S′,D_map)作为记录在L中的嵌入位置的信息填充在Top的后边,记在H中填充的D元素的最后一个坐标信息为Last,Last同D作为参数,与数据嵌入者和接收者共享,重组结果记为H′;
为防止重构过程中出现H溢出问题,对S和D_map执行Step 2后,再执行Step 3,可有效避免位置溢出问题.
2.4 图像加密图像所有者随机选取r,有r∈ Zn*,1≤i≤M,1≤j≤N,并利用公钥K1=(n, g)对H′和L分别进行加密,加密过程可以表示为
| $ {c_{{h_{i, j}}}} = E({h_{i, j}}, {r_{i, j}}) = {g^{{h_{i, j}}}}\cdot{r^n}{\rm{mod}}\;{\mathit{n}^2}, \;{\rm{ }}{c_{{l_{i, j}}}} = E({l_{i, j}}, {r_{i, j}}) = {g^{{l_{i, j}}}}\cdot{r^n}{\rm{mod}}\;{\mathit{n}^2}. $ |
注意:由定理1,当g的阶满足是n的非零整数倍时,c=E(m,r)是双射,这就保证对m加密有唯一值和其对应,目的是可逆提取,使接收者接收到嵌入秘密数据的密文图像后,可直接在密文数据中提取数据.
2.5 数据嵌入与提取 2.5.1 数据嵌入首先把秘密信息W分成n组,记为w1,w2,w3,…,wn,每组占用连续的y个比特,分别为wt1,wt2,…,wty,可以表示为
| $ {w_t} = \sum\limits_{k = 0}^y {{w_{tk}}\cdot{2^{k - 1}}}, $ |
式中:t是W被分割的第t组,t∈[1, n]且为整数.对wt进行Paillier同态公钥加密,加密结果cwt可以表示为
| $ {c_{{w_t}}} = E\left( {{w_t}, r} \right) = {g^{{w_t}}}\cdot{r^n}{\rm{mod}}\;{\mathit{n}^2}. $ |
若第n组占用比特数不足y个就以0填充,提取的时候舍掉即可.
数据嵌入者将密文图像分割成HE和LE,用公钥K1加密共享参数D,由定理1知,D对应的密文数据cD是唯一的.因此,嵌入者可找到LE中与cD相等的元素,并通过同态相乘:
| $ {c_D} = E\left( {p, r} \right) = {g^D}\cdot{r^n}{\rm{mod}}\;{\mathit{n}^2},\ {{c'}_D} = {c_D}\cdot{c_{{w_i}}} = {g^{{w_i} + D}}\cdot{r^n}{\rm{mod}}\;{\mathit{n}^2}, $ |
完成秘密数据的嵌入,此嵌入过程相当于wi加D的结果.最后,若有c′D=cli, j,将其坐标位置记为奇异位置并作为辅助信息P,P同共享参数D、Last作为嵌入秘钥K,同嵌入数据的密文图像I′E一并发送给接收者.
2.5.2 数据提取与载体恢复1) 直接在密文域中提取.对于2个互质的整数y和z,存在一个整数ζ满足:y·ζ=1mod z,则ζ称为模乘法逆元, 利用此特性可以实现模除法运算.假设一个整数x<z,记v=x·ymod n2,通过v乘以y的模乘法逆元ζ即可分离出相对应的x,实现模运算的除法为v·ζ=x·y·ζ=xmod z.
定理2 对∀a∈ZN2*,即a与N2互质,存在一个整数a,满足:a·a=1mod N2,其中a就是a的模乘法逆元,而且对于任意的a,可通过扩展欧几里得算法求得a[12].
接收者通过同态相乘嵌入秘密数据c′D=cD·cwi,可以直接用c′D乘以cD的模乘法逆元
提取完成后,再根据嵌入秘钥K即可恢复原始秘密数据.
2) 接收者只解密.接收者首先利用私钥K2分别对携带秘密数据M的HE和LE进行解密,对HE的解密结果是获得Top和Mid,根据加密约定,利用L′S和S′恢复原始高位位平面H,而后进行图像重构逆操作,即可100%恢复原始明文图像I.
3) 明文中提取.在解密过程中100%恢复H,但是对于I只是利用私钥解密,而没有还原L中的D元素.因此,这个解密过程得到的是类似原始图像I″,其低位位平面为L″,根据H中的位置信息D_map提取数据,则
| $ {{L''}_{i, j}} = D({L_{{E_{i, j}}}}) = \frac{{L(L_{{E_{i, j}}}^\lambda {\rm{mod}}\;{\mathit{n}^2})}}{{L({g^\lambda }{\rm{mod}}\;{\mathit{n}^2})}}{\rm{mod}}\;\mathit{n, } $ |
式中:L″i, j是LE解密后的数据,而后对其进行减法运算即可恢复明文为w=L″D(i, j)-LD(i, j),其中L″ D(i, j)和LD(i, j)分别是解密后的携密D元素和原始D元素,即可提取出w.
3 实验及结果分析为检验算法性能,采用Matlab2015b软件进行仿真实验,测试图像来自USC-SIPI图像库.
3.1 嵌入率分析和峰值信噪比Baboon等9幅图像在不同x值下的载体最大嵌入率如表 1所示,当x∈{1, 6, 7}时图像的嵌入率为0,这是由于图像重构阶段高位位平面压缩效果不佳造成的,H不足以存储对其进行压缩产生的S,因此不能嵌入秘密数据,所以嵌入率为0;x∈[2, 5]时,随着高位位平面每个元素所占用比特位的增加,图像嵌入率呈不断减小趋势,这是因为随着x的增加,H中相邻元素间的相关性有所减小,导致压缩冗余空间变小,所存储的D元素的位置信息变少,而且低位位平面L中每个元素所占比特数减少,嵌入数据的D元素一次嵌入的比特数也随之减少,所以嵌入率会相对变小.但是,当x∈{2, 3}时,部分图像(如F16,Splash等)在x=2时的嵌入率低于x=3时的嵌入率,这是因为图像载体具有较好的平滑度,当x=3时H压缩效果较好,能预留出足够供D元素的位置信息填充的冗余空间.
|
|
表 1 不同x值下的载体最大嵌入率 Table 1 The maximum embedding rate of the different x |
文献[5]和文献[6]算法的最大嵌入率如表 2所示,并与表 1进行了对比,发现在秘密数据嵌入率方面,以Lena图为例,本文算法中Lena图在x=3时的最大嵌入率为0.139 bpp,而文献[5]和文献[6]算法中最大嵌入率仅为0.002 6 bpp和0.049 9 bpp,本文算法中最大平均嵌入率为0.128 bpp,而文献[5]和文献[6]算法的最大平均嵌入率分别为0.002 9 bpp和0.022 0 bpp,本文算法在嵌入率方面要优于文献[5]和文献[6]算法.在直接解密与提取后再解密两种情况下,PSNR都是无穷大,可知在这两种情况下图像都可100%恢复.
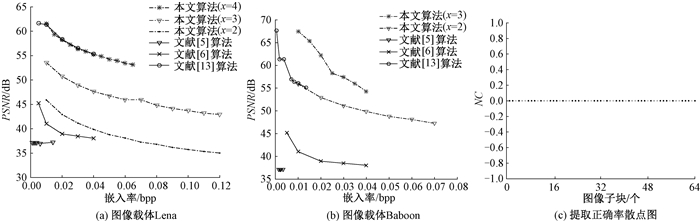
图 3(a)和(b)分别是以Lena和Baboon图像为载体直接解密,得到的嵌入率和PSNR关系图,并与文献[5]、[6]、[13]算法进行了对比.当x=4时,以Lena图为例,本文算法在嵌入率和PSNR方面的性能明显优于文献[5]和文献[6]算法,在嵌入率不超过0.04 bpp的情况下,本文算法与文献[13]算法在PSNR方面的性能相似,但是当嵌入率超过0.04 bpp时,本文算法PSNR值高于文献[13]算法,在此情况下嵌入率最高能达0.071 bpp;当x等于3或2时,如图 3(a)所示,在嵌入率不超过0.04 bpp的情况下,本文算法的PSNR值小于文献[13]算法的PSNR值,这是因为随着x的减小,低位位平面中D元素一次嵌入数据的比特位数增加,所以对原始像素的破坏增加.因此,在此情况下本文算法在PSNR方面不如文献[13]算法,但是嵌入率得到了提高,x=3和x=2时的最大嵌入率约等于0.126 bpp,而其对应的PSNR值分别是42.93 dB和35.03 dB,这是因为在x=3时一次性改变L中5 bit数据嵌入信息,在x=2时一次性改变L中6 bit数据嵌入信息,所以在嵌入率相等时x=2条件下PSNR值会变小.如图 3(b)所示,图像载体Baboon的嵌入率与PSNR的对比试验,其结果分析与Lena图相似.
|
图 3 嵌入率和PSNR的关系((a)、(b))及提取正确率散点图(c) Figure 3 The relationship between embedding rate and PSNR ((a), (b)) and scatter plot of extracted correct rate (c) |
在一个码字集合中,定义任意两个码字之间对应位上码元取值不同的位数,为这两个码字之间的汉明距离,即
| $ \begin{array}{l} N{C_{i, j}}({I_{i, j}}, {{I'}_{i, j}}) = \sum\limits_{k = 0}^7 {\sum\limits_{k' = 0}^7 {({b_k} \oplus {{b'}_k})} }, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;NC = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {N{C_{i, j}}} }, \end{array} $ |
式中:NCi, j(Ii, j, I′i, j)表示Ii, j和I′i, j之间的汉明距离,Ii, j和I′i, j是原始像素和提取后的像素;bk和b′k分别表示Ii, j和I′i, j的第k个比特值.根据团队对64×64的不重叠图像子块的实验仿真结果,所得图像块提取正确率散点图如图 3(c)所示,其中横轴表示64个64×64的不重叠图像子块,纵轴表示提取数据的NC值.可以看出,信息提取的正确率为100%.
3.3 安全性分析本算法在图像重构阶段,根据高位位平面H的压缩与填充,预先就相当于对原始图像的像素进行了一次重构,破坏了原始图像相邻像素间的相关性.而后进行Paillier同态公钥加密后,由于在嵌入端不需要使用私钥即可通过同态乘法嵌入数据,而私钥是通过安全渠道传递给合法的接收者,非法敌手无法获取私钥.因此,携密图像在传输过程中的安全性得到了保障,敌手在仅有私钥的情况下仅能解密图像而不能提取秘密数据.综上所述,本算法确保了秘密数据的安全性.
4 结束语本算法采用像素位平面分割,而后利用Paillier同态公钥加密系统进行密文域上可逆信息隐藏,该算法保证在解密能100%恢复原始图像的前提下提高了嵌入容量,平均最高嵌入率可达0.128 bpp.理论与实验结果表明,提取与加密载体恢复实现了可分离操作.但是由于本算法是对2个位平面分别进行加密,因此算法复杂度有所增加,这也是今后需要对本算法进行改进的地方.
| [1] |
柯彦, 张敏情, 苏婷婷. 基于R-LWE的密文域多比特可逆信息隐藏算法[J]. 计算机研究与发展, 2016, 53(10): 2307-2322. DOI:10.7544/issn1000-1239.2016.20160444 (  0) 0) |
| [2] |
HSU C Y, LU C S, PEI S C. Image feature extraction in encrypted domain with privacy-preserving SIFT[J]. IEEE transaction on image processing, 2012, 21(11): 4593-4607. DOI:10.1109/TIP.2012.2204272 (  0) 0) |
| [3] |
HONG W, CHEN T S, WU H Y. An improved reversible data hiding in encrypted images using side match[J]. IEEE signal processing letters, 2012, 19(4): 199-202. DOI:10.1109/LSP.2012.2187334 (  0) 0) |
| [4] |
LIAO X, SHU C W. Reversible data hiding in encrypted images based on absolute mean difference of multiple neighboring pixels[J]. Journal of visual communication and image representation, 2015, 28: 21-27. DOI:10.1016/j.jvcir.2014.12.007 (  0) 0) |
| [5] |
ZHANG X P. Reversible data hiding in encrypted image[J]. IEEE signal processing letters, 2011, 18(4): 255-258. DOI:10.1109/LSP.2011.2114651 (  0) 0) |
| [6] |
ZHANG X P. Separable reversible data hiding in encrypted image[J]. IEEE transactions on information forensics and security, 2012, 7(2): 826-832. DOI:10.1109/TIFS.2011.2176120 (  0) 0) |
| [7] |
WU X T, SUN W. High-capacity reversible data hiding in encrypted images by prediction error[J]. Signal processing, 2014, 104(6): 387-400. (  0) 0) |
| [8] |
HUANG F J, HUNAG J W, SHI Y Q. New framework for reversible data hiding in encrypted domain[J]. IEEE transactions on information forensics and security, 2016, 11(12): 2777-2789. DOI:10.1109/TIFS.2016.2598528 (  0) 0) |
| [9] |
YIN Z X, ABEL A, ZHANG X P, et al. Reversible data hiding in encrypted image based on block histogram shifting[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Shanghai, 2016: 2129-2133.
(  0) 0) |
| [10] |
GOLDWASSER S, MICALI S. Probabilistic encryption[J]. Journal of computer and system sciences, 1984, 28(2): 270-299. DOI:10.1016/0022-0000(84)90070-9 (  0) 0) |
| [11] |
PAILLIER P. Public-key cryptosystems based on composite degree residuosity classes[C]// Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques. Prague, 1999: 223-238.
(  0) 0) |
| [12] |
DONALD E K. The art of computer programming[M]. Boston: Addison-Wesley, 1997.
(  0) 0) |
| [13] |
ZHANG W M, MA K D, YU N H. Reversibility improved data hiding in encrypted images[J]. Signal processing, 2014, 94(1): 118-127. (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


