2. 北方工业大学 数据工程研究院 北京 100144
2. Institute of Data Engineering, North China University of Technology, Beijing 100144, China
Top-k连续查询是流数据环境下的一种重要查询,已广泛应用于诸多领域。在物联网系统中,数据往往产生于多个采集终端。当这些终端向服务器发送数据时,面对复杂且不稳定的网络环境,会经常发生数据重传和数据拥塞,导致数据的产生顺序和到达服务器的顺序发生变化,数据流中充斥着大量乱序数据。数据流乱序的情况给数据流的top-k连续查询带来了挑战,top-k连续查询的实施基于滑动窗口,滑动窗口分为基于时间的滑动窗口和基于元组个数的滑动窗口。如果没有特别说明,本文的滑动窗口是指基于时间的滑动窗口,滑动窗口内部的数据严格根据滑动时间间隔进行划分。窗口滑动后,最早一批的数据被释放,最新一批的数据流入窗口。等到最新一批的数据全部流入窗口,窗口立即闭合并执行计算任务。根据滑动窗口这种严格按时间划分的机制,针对滑动窗口内部的每一批数据,当数据存在乱序时,边界元组有可能会迟到。由于窗口已经闭合并立即进行计算,边界元组不能包含在正确的窗口内,会造成查询结果错误。
目前处理乱序流的主流方法是基于缓存的方法。基于缓存的方法使用开辟的缓冲区等待迟到数据,对缓冲区内数据进行排序,以避免系统处理乱序数据。传统的基于缓存的K-slack[1]方法和MP-K-slack[2]方法无法做到对缓冲区大小自适应,在时延变小的情况下会浪费系统资源。AQ-K-slack[3]虽然实现了缓冲区自适应,但无法应用于top-k连续查询这类复杂的聚合函数。在具体的top-k连续查询算法中,SMA算法[4]利用k-skyband对象在有序流上快速进行top-k连续查询,但需要维护大量的k-skyband对象,内存耗费大,并且该方法只能在有序流上使用。MinTopk算法[5]维护了一个最小的top-k候选集,每次计算都从该候选集中得出结果,大大减少了计算量,但在乱序流上使用会有误差。GSTopk算法[6]对MinTopk算法进行了一些改良,使其能在乱序流下立刻给出近似结果,可以在时效性要求较高的情况下使用。在上述算法的基础上,本文提出一种面向高速乱序数据流的top-k连续查询方法。首先使用基于缓存的乱序流处理技术,舍弃缓存数据重排序步骤,缓存时长的确定使用缓存时长自适应算法,在保证用户允许的最小正确率的情况下计算出最小缓存时长,其次使用改造的MinTopk算法计算当前窗口的top-k结果集。实验结果表明,该方法能有效权衡查询精度和查询时延之间的关系,对窗口内数据执行快速且高效的查询并得出结果,使乱序流下的top-k连续查询收到了良好的效果。
1 相关工作在乱序数据流处理方面,研究工作按处理机制的不同大致分为基于缓存的方法[1-3, 7-8]、基于标点的方法[9-12]、基于推测的方法和基于近似的方法。基于缓存的方法是开辟缓冲区来缓存乱序数据以等待迟到数据,以一定延迟开销换取结果质量的提升。K-slack[1]是基于缓存的典型方法,其中参数K与缓冲区的大小密切相关。具体来说,K-slack技术维护缓冲区用来缓存到达的元组,缓冲区内的数据最多等待K个时间单位,然后被提交至查询处理模块进行查询。MP-K-slack方法[2]是基于流元组延迟的动态变化来不断调整K值,如果延迟不断增大,会使数据越积越多,导致查询时延的上升和查询吞吐量的下降。AQ-K-slack方法[3]以用户给定的结果精度为目标,通过聚合函数与窗口覆盖率的定值关系,动态调整K值大小。但由于top-k查询这类聚合函数过于复杂,会造成AQ-K-slack方法难以实施。另外,基于缓存的方法大多会对缓存的数据进行排序,以保证计算时的有序,代价比较大。基于标点的方法依赖于数据流内被称为标点的特殊元组,表示没有时间戳小于标点的元组。当收到一个标点,查询算子确定未来将没有数据到达,然后得到这些窗口的查询结果[10],如心跳[12]、部分排序[11]是标点的特殊类型。标点显式地通知查询算子什么时候返回窗口的结果,因此查询算子能够直接消费无序输入。然而,查询结果的准确性从根本上会受到标点准确性的限制[9]。假定标点是由外部数据源提供,或者是由应用程序语义和数据流乱序特征的先验知识通过系统非常简单地生成,但这个假设不一定在现实世界的场景中成立。基于推测的方法和基于近似的方法基本上采用了激进处理方法。激进处理方法与保守等待方法相反,它不管乱序问题是否存在,总是优先快速地处理数据流,直到迟到元组出现以后再弥补错误。激进处理方法通常应用于实时性要求较高且急需获取处理结果的分析处理系统。但是这种方法的场景局限性很大,并且有可能得不到正确结果。
在top-k连续查询具体算法方面,SMA算法[4]根据数据特征提出k-skyband对象的概念。该算法需要维护k-skyband对象之间的支配关系,总体代价较大,并且不具备过滤新增数据(即新流入窗口的数据)的能力,不能处理乱序数据流。MinTopk算法[5]维护了一个最小top-k候选集,对于流入窗口的新元组,高效地过滤掉不可能成为top-k结果的元组,将可能成为top-k结果的元组插入候选集,每次只要查找候选集即可找到top-k结果。但是该算法只能处理顺序流,在乱序流中会导致查询错误。GSTopk算法[6]改造了MinTopk算法,使其能够快速地处理乱序数据流,但是该算法得出的仅仅是当前窗口内的top-k结果,没有对当前窗口的迟到数据进行处理,导致其计算结果往往不够准确。由于该算法的高效性,在正确率要求不高而实时性要求特别高的情况下可以使用。基于以上研究,本文使用基于缓存的乱序处理方法等待迟到元组,但不对缓冲区内数据进行排序,配合使用改造的MinTopk算法,保证top-k连续查询正确率在用户可接受范围内,减少了查询时延。
2 面向高速乱序流的top-k连续查询方法图 1为面向乱序流的top-k连续查询算法流程。为了解决乱序数据流中top-k连续查询结果不准确的问题,使用基于缓存的乱序流处理方法,该方法的难点在于缓存时长的确定。基于缓存的方法不可能无限等待迟到元组,不能保证查询的绝对正确性。使用缓存时长自适应算法对top-k查询进行正确率和缓存时长的统计,在保证用户允许的最小正确率的情况下,周期性地计算出所需要的最小缓存时长。接下来通过具体的top-k查询方法,计算出当前窗口的top-k结果。为了方便计算,灵活地实施缓存时长自适应算法,使用元组的Event Time[13]划分窗口,也就是使用元组自身的时间戳作为滑动窗口的划分依据。

|
图 1 面向乱序流的top-k连续查询算法流程 Fig. 1 Algorithm flowchart of continuous top-k query over out-of-order data streams |
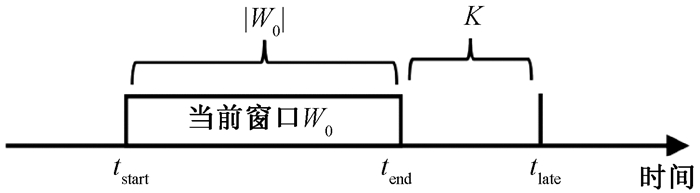
图 2为基于缓存的乱序流处理方法。当前滑动窗口为W0,W0在tend时刻闭合,闭合后等待K个时间单位,即在tlate时刻计算并输出W0的top-k结果。在这K个时间单位中,对于到来的每一个元组,若其属于当前滑动窗口W0,该元组就会被发送到W0处理;若其属于W0前面或后面的窗口,则进行相应的处理。
|
图 2 基于缓存的乱序流处理方法 Fig. 2 Cache-based out-of-order data streams processing approach |
基于缓存的乱序流处理方法,其难点在于缓存时长K的确定。缓存时间越长,时延越高,正确率也就越高。网络延迟的制约因素有很多,不可能准确地计算出最晚元组到达的时间。另外,在高速乱序数据流下,数据流量巨大,缓存时间越长,对缓冲区和系统吞吐量造成的压力越大。因此,在保证用户允许的最小正确率的情况下选择一个恰当的缓存时长K,可以有效地缓解系统压力,减少查询时延。
计算单次的top-k结果的正确性是没有意义的,但统计多次的top-k结果的正确率足以证明某种方法的有效性。所以,通过统计不同缓存时长下top-k查询结果的正确率,以质量驱动的方式[3]选出最小缓存时长,即在保证用户允许的最小正确率的情况下计算出最小缓存时长。具体步骤如下。
1) 参数初始化。系统指定一个初始缓存时长K,即窗口的缓存时长到达K时输出查询结果。初始化用于计算恰当缓存时长的区间,用(Kdown, Kup]表示。在初始情况下,(Kdown, Kup]将被初始化为(0, K]。另外,需要用户指定能承受的最小正确率εmin。
2) 统计计算。将(Kdown, Kup]平均划分得到m个缓存时长,即{Kdown+(Kup-Kdown)/m, Kdown+2*(Kup-Kdown)/m, …, Kdown+(m-1)*(Kup-Kdown)/m, Kup}。对于每次top-k查询,记录下这m个不同缓存时长得到的top-k结果集,同时, 后台等待所有的迟到元组计算出此次查询正确的top-k结果集。对于每一个缓存时长对应的top-k结果集,将其与正确的结果集进行比较,计算该top-k结果集的命中率,即top-k结果集与正确结果集一致的项数与总项数的比值。经过n次top-k查询取平均值,就能计算出不同缓存时长的查询准确率。
3) 求最小缓存时长。根据用户给定的所能承受的最小正确率εmin,即可定位出可以达到该正确率的最小缓存时长所在的区间(Kdown, Kup],那么最小缓存时长Kmin改为Kup。若此时符合要求的缓存时长不在(Kdown, Kup]内,则区间相应前移或者后移(Kup-Kdown)/m个单位。为了避免区间太小,收敛速度太慢,(Kup-Kdown)/m不能太小。重复上一个步骤,统计出(Kdown, Kup]中不同缓存时长对应的正确率。
表 1为根据不同缓存时长统计的top-3查询结果示例。当前缓存时长区间为(0 s, 4.5 s],Kmin=4.5 s,m=3,n=20,εmin=0.8,则平均划分为1.5 s、3 s、4.5 s三个缓存时长。在每次top-3查询中,记录下这三个缓存时长对应的top-3结果,最后和此次查询正确的top-3结果集进行比较,得到这三个缓存时长对应结果的命中率。这个过程重复20次,每一个缓存时长会得到一个查询正确率。其中,缓存时长为1.5 s的正确率为72%,缓存时长为3 s的正确率为83%,缓存时长为4.5 s的正确率为94%。由于用户允许的最小正确率εmin=0.8,所以下一次用于计算最小缓存时长的区间改为(1.5 s, 3 s],最小缓存时长Kmin改为3 s,重复进行以上操作。
|
|
表 1 不同缓存时长的统计结果示例 Tab. 1 Examples of statistical results for different cache duration |
Top-k连续查询依托于滑动窗口模型,给定滑动窗口W和top-k查询q,每当窗口滑动后,q返回W中分值最高的k个元组。由于算法需要实时处理大量数据,且每次窗口滑动前后有大量重叠数据,计算这些重复数据耗时费力。因此,本文借鉴MinTopk算法的思想,利用滑动窗口的特性过滤掉大量对结果无贡献的元组,维护一个top-k结果候选集C。当窗口滑动后,更新候选集C,只需要访问候选集C便可得出top-k结果集,这样既大大削减了数据规模[14],又保证了查询结果的准确性。
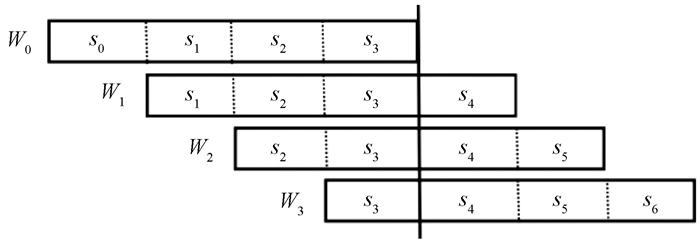
图 3展示了相邻滑动窗口的数据归属,其中Wi表示某编号窗口,si表示由滑动步长划分的某批数据。每次窗口滑动后,最早的一批数据被释放,最新的一批数据流入窗口。新来的元组有可能一直成为top-k结果,直到它被窗口释放。如s3中的某元组可能成为W3或W2、W1、W0的top-k结果。可以看出,W0包含所有批次数据,W1包括批次s1、批次s2、批次s3的数据,W2包括批次s2、批次s3的数据,W3仅包括批次s3的数据。对于W0中的数据,为了避免重复计算,首先计算出W3(s3)的top-k结果集,然后计算出W2(s2和s3)的top-k结果集,再计算出W1(s1、s2和s3)的top-k结果集,最后计算出W0的top-k结果集。如此计算则可以充分利用上一次的计算结果,避免重复计算。
|
图 3 相邻滑动窗口的数据归属 Fig. 3 Data attribution of adjacent sliding windows |
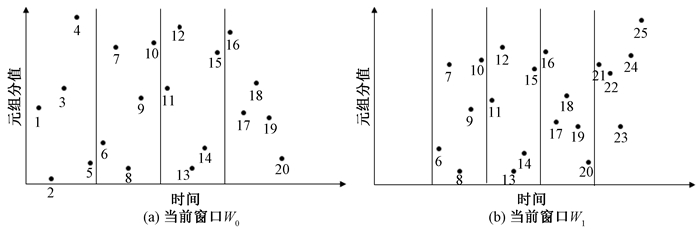
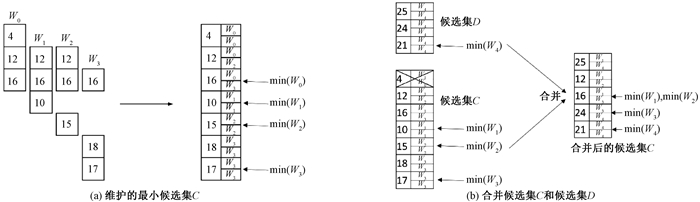
图 4为不同窗口的示例数据,图 5为候选集C和候选集D。如图 4(a)所示,当前窗口为W0,每个元组的标签表示元组的到达顺序。如图 5(a)所示,仅对于W0窗口中的元组,计算出窗口W0、W1、W2、W3的top-3结果集,使用一个有序列表来维护这些元组。如图 5(b)所示, 按元组分值从大到小排列,元组右侧表示该元组会对哪些窗口做出贡献,这个有序列表就是候选集C。由于一个元组作出贡献的窗口集合是连续的,只维护起始贡献窗口id和结束贡献窗口id即可。同时,为了快速过滤掉不作贡献的元组,还需要维护各个窗口的最小元组指针。由于候选集列表C是有序的,所以当前窗口的top-k结果集为候选集C前k个元组的集合。
|
图 4 不同窗口的示例数据 Fig. 4 Sample data for different windows |
|
图 5 候选集C和候选集D Fig. 5 Candidate list C and candidate list D |
由于本文算法的复杂性,为了避免在极端情况下对维护的候选集列表C进行频繁插入,需要对原MinTopk算法进行改造后使用。当窗口滑动后,对应图 2中[tstart, tlate]时刻,对于其中的每一个元组有可能属于前面窗口,或属于当前窗口,或属于下一个窗口。并且由于需要维护不同缓存时长的top-k结果,所以不仅要维护前面窗口不同缓存时长的top-k结果,还需要维护当前窗口的候选集C和下一批次数据的top-k结果D。下面给出tlate时刻执行计算的具体流程。
1) 获取当前top-k结果。此时,当前窗口候选集列表C中的前k个元组为当前窗口的top-k结果。创建一个空的候选集列表,将当前窗口的top-k结果复制到该列表,用以后台继续记录不同缓存时长的top-k结果。
2) 删除过期元组。把当前窗口候选集列表C中最早一批元组(即候选集列表前k个元组)的起始贡献窗口id加1。当起始贡献窗口id大于结束贡献窗口id时,该元组被淘汰,从列表中删除。
3) 合并候选集列表D到候选集列表C。通过指针索引,对于候选集列表D中的每一个元组,按从小到大顺序和各个窗口的元组最小分值进行比较,快速计算出起始贡献窗口id和结束贡献窗口id。若其对某个窗口有贡献,将其插入到候选集C中,使C保持有序,同时删除对候选集C不作贡献的元组。
对于当前窗口之前的窗口,针对不同的缓存时长,记录每个窗口的top-k结果,对于晚到的元组持续进行处理,直到该窗口没有元组到达。如图 4(b)所示,窗口滑动后,当前窗口由W0变为W1,新流入了元组21~25,元组1~5被释放。图 5(b)展示了候选集C和候选集D的合并过程。对于元组25,依次和元组17、元组15、元组10进行比较,得出元组25的起始贡献窗口为W1,结束贡献窗口为W4,并将其有序地插入候选集C中。
3 实验效果评价 3.1 实验过程实验环境使用CPU为3.2 GHz,内存为16 GB的ubuntu18.04电脑。缓存时长自适应算法的实验参数如下:缓存时长K初始为2 s,缓存时长划分份数m为10,迭代次数n为30,允许的最小正确率εmin为0.95;top-k查询的实验参数如下:偏好函数为求元组最大值,k值为5,滑动窗口总大小为60 s,滑动窗口的滑动步长为5 s。
由于网络延迟通常遵循指数分布等长拖尾型概率分布[15],故使用指数分布生成乱序数据。为了营造高速乱序流的环境,尽量增大窗口中的元组数目。另外,生成的数据应包含时间戳字段、值字段。通过指数分布生成了充足的乱序数据,选择SMA算法、MinTopk算法、GSTopk算法作为本实验的对比算法,使用相同的数据进行top-k连续查询,记录下运行参数,得出top-k结果正确率与算法运行时间的关系以及top-k结果查询时延与算法运行时间的关系。
为了测试算法对乱序程度不同的数据的有效性,构造一个定量的数据集,并将其打乱为三种不同乱序程度的数据集。本文算法和对比算法分别使用三种不同乱序程度的数据集作为输入进行top-k连续查询,并记录下运行参数,得出top-k结果正确率与数据乱序程度的关系。另外,为了避免偶然性所带来的实验误差,以上所述实验均在参数及数据不变的情况下进行多次,并取平均值作为最终实验结果。
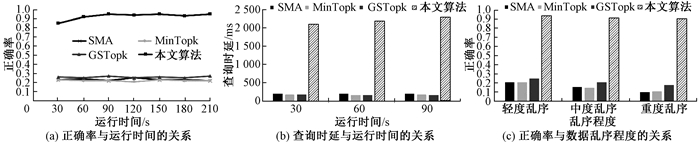
3.2 实验结果分析不同算法的实验结果对比如图 6所示。图 6(a)展示了随着运行时间的增加,不同算法的正确率变化情况。可以看出,本文算法比其他算法的正确率高很多,显示了本文算法处理乱序流的优越性。这是由于本文算法使用基于缓存的方法等待迟到元组,使边界元组被包含在正确的滑动窗口内,提高了正确率。本文算法的正确率随着运行时间一直在变化,这是由于本文算法可以根据数据流的乱序程度自适应缓存时长。若当前缓存时长的正确率大于允许的最小正确率,则应减小缓存时长;否则进行相反的操作。图 6(b)展示了随着运行时间的增加,不同算法的查询时延变化情况。查询时延表示当滑动窗口闭合后到计算得出该滑动窗口的top-k结果集所需要的时间。可以看出,本文算法的查询时延比其他三种算法的查询时延要高。这是由于本文算法使用了基于缓存的乱序流处理方法,等待属于当前滑动窗口的迟到元组,以时延换取了正确率的上升。随着运行时间的改变,查询时延还会不断变化。这是由于本文算法可以自适应改变缓存时长,使得时延增大,正确率提高。当面临实时性要求特别高而正确率要求不太高的情况,应尽量避免使用本文算法。GSTopk算法可以快速处理乱序数据流,只是结果不是那么精确。由此可见,本文算法的一个缺点是查询时延较高。图 6(c)展示了数据集轻度、中度和重度乱序时,不同算法的正确率变化情况。在乱序数据集上,随着乱序程度的增加,SMA算法和MinTopk算法的正确率偏低,这是由于这两种算法没有针对乱序数据流做处理,属于当前滑动窗口的迟到数据被丢弃或者是延迟到下一个窗口执行,导致查询结果不准确。GSTopk算法可以处理乱序流,但正确率也较低,而本文算法的正确率较高,证明本文算法适合处理乱序数据流下的top-k连续查询问题。
|
图 6 不同算法的实验结果对比 Fig. 6 Comparison of experimental results of different algorithms |
本文研究了高速乱序流环境下的top-k连续查询问题,尽管已有一些相关方法研究了此类问题,但是查询结果误差较大。本文通过已有的乱序流处理方法和滑动窗口的数据特征,首先使用基于缓存的方法等待迟到元组,但不对缓冲区排序,并运用统计的思想实现了缓存时长自适应。然后使用改造的MinTopk算法,在保证用户允许的最小正确率的情况下计算出最小缓存时长,减少了查询时延。后续工作将优化缓存时长自适应算法,减小算法资源消耗,进一步加快算法的计算速度。
| [1] |
ABADI D J, CARNEY D, CETINTEMEL U, et al. Aurora: a new model and architecture for data stream management[J]. The VLDB journal, 2003, 12(2): 120-139. DOI:10.1007/s00778-003-0095-z (  0) 0) |
| [2] |
MUTSCHLER C, PHILIPPSEN M. Distributed low-latency out-of-order event processing for high data rate sensor streams[C]//Proceedings of the IEEE 27th International Symposium on Parallel and Distributed Processing. Piscataway: IEEE Press, 2013: 1133-1144.
(  0) 0) |
| [3] |
JI Y Z, ZHOU H J, JERZAK Z, et al. Quality-driven processing of sliding window aggregates over out-of-order data streams[C]//Proceedings of the 9th ACM International Conference on Distributed Event-based Systems. New York: ACM Press, 2015: 68-79.
(  0) 0) |
| [4] |
MOURATIDIS K, BAKIRAS S, PAPADIAS D. Continuous monitoring of top-k queries over sliding windows[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data. New York: ACM Press, 2006: 635-646.
(  0) 0) |
| [5] |
YANG D, SHASTRI A, RUNDENSTEINER E A, et al. An optimal strategy for monitoring top-k queries in streaming windows[C]//Proceedings of the 14th International Conference on Extending Database Technology. New York: ACM Press, 2011: 57-68.
(  0) 0) |
| [6] |
朱睿, 王斌, 杨晓春, 等. 基于高速乱序流的top-k连续查询算法[J]. 计算机学报, 2018, 41(8): 1693-1708. ZHU R, WANG B, YANG X C, et al. Continuous top-k query over high speed unorder streaming data[J]. Chinese journal of computers, 2018, 41(8): 1693-1708. (  0) 0) |
| [7] |
杨宁, 许嘉, 吕品, 等. 基于混合处理模型的乱序数据流分布式聚合查询处理技术[J]. 广西科学, 2019, 26(4): 398-404. YANG N, XU J, LV P, et al. Distributed aggregation query processing technology for out-of-order data streams based on hybrid processing model[J]. Guangxi sciences, 2019, 26(4): 398-404. DOI:10.3969/j.issn.1005-9164.2019.04.007 (  0) 0) |
| [8] |
周春姐, 戴鹏飞, 李洪波, 等. 物联网中具有时间持续性特征的乱序事件查询处理技术研究[J]. 计算机科学, 2016, 43(5): 179-187. ZHOU C J, DAI P F, LI H B, et al. Research of interval-based out-of-order event processing in Internet of Things[J]. Computer science, 2016, 43(5): 179-187. (  0) 0) |
| [9] |
KRISHNAMURTHY S, FRANKLIN M J, DAVIS J, et al. Continuous analytics over discontinuous streams[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data. New York: ACM Press, 2010: 1081-1092.
(  0) 0) |
| [10] |
LI J, MAIER D, TUFTE K, et al. Semantics and evaluation techniques for window aggregates in data streams[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data. New York: ACM Press, 2005: 311-322.
(  0) 0) |
| [11] |
LIU M, LI M, GOLOVNYA D, et al. Sequence pattern query processing over out-of-order event streams[C]//Proceedings of the IEEE 25th International Conference on Data Engineering. Piscataway: IEEE Press, 2009: 784-795.
(  0) 0) |
| [12] |
SRIVASTAVA U, WIDOM J. Flexible time management in data stream systems[C]//Proceedings of the 23rd ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems. New York: ACM Press, 2004: 263-274.
(  0) 0) |
| [13] |
AKIDAU T, SCHMIDT E, WHITTLE S, et al. The dataflow model: a practical approach to balancing correctness, latency, and cost in massive-scale, unbounded, out-of-order data processing[J]. Proceedings of the VLDB endowment, 2015, 8(12): 1792-1803. DOI:10.14778/2824032.2824076 (  0) 0) |
| [14] |
王青, 谭良, 杨显华. 基于Spark的Apriori并行算法优化实现[J]. 郑州大学学报(理学版), 2016, 48(4): 60-64. WANG Q, TAN L, YANG X H. Optimization of Apriori parallel algorithm based on Spark[J]. Journal of Zhengzhou university (natural science edition), 2016, 48(4): 60-64. (  0) 0) |
| [15] |
曹原, 刘英博, 肖利, 等. 状态监测数据流时间乱序问题建模与研究[J]. 计算机集成制造系统, 2013, 19(12): 2960-2967. CAO Y, LIU Y B, XIAO L, et al. Modeling on time out-of-order problem of condition monitoring data stream[J]. Computer integrated manufacturing systems, 2013, 19(12): 2960-2967. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


