2. 苏州大学 江苏省计算机信息处理技术重点实验室 江苏 苏州 215006;
3. 苏州大学 东吴学院 江苏 苏州 215006
2. Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Suzhou 215006, China;
3. Soochow College, Soochow University, Suzhou 215006, China
强化学习属于机器学习的一个分支,具有很强的通用性,可以被应用于各个领域,如博弈论、控制论、运筹学、遗传算法等[1-3]。由于强化学习算法与动态规划[4-7]息息相关,智能体所交互的环境通常使用马尔可夫决策过程(Markov decision process,MDP)进行建模。相比于传统的控制算法,强化学习算法并不要求MDP的状态转移概率是已知的,因此可以适应极其复杂的环境。与机器学习的另一个分支监督学习不同的是,强化学习中没有用来训练的输入-输出序列,所以无法像监督学习一样在每一个时间步精准地评价智能体选择的动作是否正确。同时,强化学习更强调与环境的交互及实时决策,需要考虑探索与利用的权衡问题。为了促进智能体的探索,通常采用ε-greedy策略,即在每个时间步下,智能体有ε的概率随机选择动作,有1-ε的概率根据最优策略选择动作。
智能体的最终目的就是最大化累积奖励值。强化学习同时兼顾了长期奖励值与短期奖励值,它已经成功地被应用于各个领域,如自动驾驶、机器人控制、调度问题、通讯、围棋等[5]。
强化学习算法主要分为基于值函数的算法与基于策略梯度的算法[8-11]。基于值函数的算法包括Q-learning、Sarsa、蒙特卡洛等,其基本思想是在学习过程中计算某个策略的期望奖励值,从而选择估计值更高的策略,并最终收敛到一个最优策略。Q-learning属于典型的离线学习策略,Sarsa则属于在线学习策略。传统的基于值函数的算法可以很好地解决状态动作空间为离散的学习问题,然而对于连续的环境,传统算法会遭遇“维数灾难”问题[12-16]。深度学习[17]作为机器学习的一个分支,具有强大的数据拟合能力,能够从大规模的数据中寻找相应的规律。因此研究人员将深度学习的数据处理能力和强化学习与环境进行交互的能力结合起来,提出了深度强化学习。研究人员提出了DQN模型[18],利用深度神经网络拟合与更新Q函数,在复杂的雅达利游戏平台上取得了超过人类专家的效果。由于原始的DQN只使用单个神经网络,因此存在计算目标值与更新神经网络依赖性过强的问题,不利于神经网络的收敛。为了解决这一问题,人们提出了NatureDQN,使用两个网络进行训练,在此基础上,进一步提出了DoubleDQN[19],解决了Q-learning固有的过估计问题。同时,为了提高样本利用的效率,人们提出了prioritized replay DQN,优先利用经验池中重要性更高的样本。DuelingDQN[20]增加了优势函数模块,提升了模型的稳定程度。强化学习算法的基于策略梯度算法是直接对参数化的策略空间进行搜索,即对策略空间进行求导来更新策略参数。
把强化学习的两种算法结合起来便形成了演员-评论家(actor-critic,AC)算法,其中演员负责选择动作并与环境进行交互,评论家用以评估动作的好坏。AC算法是当前强化学习中应用最为广泛的算法,在游戏、机器人控制等领域取得了良好的效果。研究人员也因此提出了针对AC的一系列改进算法。异步梯度更新(asynchronous advantage actor-critic,A3C)[1]同时运行多个线程与环境进行交互,减少了经验项之间的相关性,改善了收敛性。确定性策略梯度算法(deterministic deep policy gradient,DDPG),缓解了随机策略样本需求量过大的问题。优势函数AC算法(advantage actor critic,A2C)使用优势函数代替了动作值函数,使得学习过程更加稳定。对于深度强化学习算法来说,学习率的设置是一个至关重要的问题:若学习率设置得过小则神经网络会收敛得很慢,若学习率设置得过大,则会造成学习不稳定等问题。基于信赖域的AC算法(trust region policy optimization,TRPO)在每一步的更新过程中添加了相应的约束条件,保证了学习效果的稳定提升。由于TRPO的计算量较大,近端策略优化算法(proximal policy optimization,PPO)利用一阶近似简化了计算量而保证了与TRPO相同的效果。由于PPO能够实现平稳的学习过程,本文将在CMDP的基础上实现平衡的强化学习。
1 相关工作传统强化学习算法的目标通常是针对单个目标进行优化,然而现实生活中的控制规划问题通常都涉及若干个目标,并且各个目标之间常常是相互冲突的。例如对于一个扫地机器人来说,其目标是清洁尽可能多的面积同时降低电力损耗[10]。在设计通信网络时,由于网络总的传输能力是有限的,设计者需要同时考虑数据传输效率与传输延迟这两个目标[12]。在自动驾驶领域,设计汽车的自动控制算法时要同时考虑能源效率、路径规划、驾驶员安全等因素。多目标强化学习算法作为目前强化学习算法的一个分支可以用来解决涉及多个目标的问题,即同时对多个目标进行优化。然而现实生活中人们通常只关心单个目标是否最优而其他目标只需要保持在底线值之上。CMDP能更准确地描述此类问题。在CMDP中,受限算法的目标是最优化单个目标并确保其他目标高于某个具体的值。与MDP类似,CMDP对于每个目标的状态值定义为
| $ V(S)=E\left[\sum\limits_{t} \gamma^{t} r\left(s_{t}, a_{t}\right) \mid s_{0}\right], $ |
该值函数为Bellman方程的解
| $ V(S)=E\left[r(s, a)+V\left(S^{\prime}\right)\right] \text { 。} $ |
目标为最大化总体奖励值
| $ \max \limits_{\varPi \in I} Q^{\pi}=E\left[\sum\limits_{t} \gamma^{t} r_{t}\right]=\sum\limits_{s \in S} \mu(s) V(s), $ |
在此基础上,CMDP添加了额外的约束项
| $ V_{C}(S)=E\left[\sum\limits_{t} \gamma^{t} c\left(s_{t}, a_{t}\right) \mid s_{0}\right]=E\left(c(s, a)+V_{C}\left(s^{\prime}\right)\right), $ |
| $ Q_{C}^{\pi}=\sum\limits_{s \in S} \mu(s) V_{C}(s) 。$ |
于是CMDP的目标可以被描述为
| $ \max \limits_{\varPi \in I} Q^{\pi} \text { s. t. } Q_{C}^{\pi} \leqslant \alpha 。$ |
多目标强化学习利用不同的权重进行学习,因此会获得多个策略,但是此种方案会消耗大量的计算资源。基于此,本文提出通过动态调整目标与约束的相对权重来实现受限强化学习的算法。即利用一个初始权重构造一个综合目标,在学习过程中,在最优化主目标的同时,不断评估约束目标是否得到了满足:若某值满足约束,则保持当前权重;而若约束值没有符合要求,则不断提高约束值对应的权重,此时智能体会更加倾向优化约束值,从而促使约束值符合要求。传统的CMDP模型是基于离散环境的,并不适用于连续的机器人环境。本文提出一种结合了CMDP算法与PPO算法的模型,称为CRODP(constrained reward optimization with dynamic priority)。该模型以CMDP为基础,并引入PPO算法使其可以处理连续的环境,根据给定的约束学习一个满足要求的策略。最后,在复杂的机器人环境中将该算法与固定权重奖励构造算法进行比较,实验结果验证了此算法的有效性。
2 基于AC框架的受限马尔可夫模型 2.1 公式构建利用拉格朗日松弛技巧[21-22],可以将原始的CMDP转化为等价的无约束问题,
| $ \begin{aligned} &\min \limits_{\lambda} \max \limits_{\theta} L(\lambda, \theta)=\min \limits_{\lambda} \max \limits_{\theta}\left[(1-\lambda)\left(Q^{\pi_{\theta}}-\alpha\right)+\right. \\ &\left.\lambda\left(Q_{C}^{\pi_{\theta}}-\beta\right)\right], \end{aligned} $ | (1) |
λ为拉格朗日系数,反映了约束值的优先级,当系数不断增大时,算法更倾向于对此项进行优化。本文使用AC算法更新策略参数θ,同时在每个情节结束时,根据约束条件的满足情况来更新λ。算法的目标是找到一个极值点(λ*, θ*),使得智能体能够学习一个满足约束的最优策略。利用梯度法,更新式(1),
| $ \frac{\partial L}{\partial \lambda}=E\left[\left(V_{C}(s)-\beta\right)-(V(s)-\alpha)\right] , $ |
| $ \frac{\partial L}{\partial \theta}=E\left(\frac{\partial \pi_{\theta}}{\partial \theta}\left((1-\lambda) Q^{\pi_{\theta}}(s, a)+\lambda Q_{C}^{\pi_{\theta}}(s, a)\right)\right), $ |
求出对λ与θ的梯度,
| $ \nabla_{\lambda} L=E\left[\left(V_{C}(s)-\beta\right)-(V(s)-\alpha)\right], $ | (2) |
| $ \nabla_{\theta} L=E\left(\nabla_{\theta} \pi_{\theta}\left((1-\lambda) Q^{\pi_{\theta}}(s, a)+\lambda Q_{C}^{\pi_{\theta}}(s, a)\right)\right) 。$ | (3) |
L对应的λ与θ的更新公式为
| $ \theta={clip}\left(\theta+\eta_{2} \nabla_{\theta} L\right), $ | (4) |
| $ \lambda={clip}\left(\lambda+\eta_{1} \nabla_{\lambda} L\right), $ | (5) |
其中:η1与η2为学习率;clip代表将每次更新后的参数值控制在某一范围内,防止参数过大或者过小。同时,为了减小训练过程中的方差,使用优势函数代替策略更新式(3)中的Q函数[1],
| $ \nabla_{\theta} L=E\left(\nabla_{\theta} \pi_{\theta}\left((1-\lambda) A^{\pi_{\theta}}+\lambda A_{C}^{\pi_{\theta}}\right)\right), $ |
其中优势函数的计算为
| $ A^{\pi_{\theta}}=\sum\limits_{i=0}^{t} \gamma^{i} r(i)-V(s), $ |
| $ A_{C}^{\pi_{\theta}}=\sum\limits_{i=0}^{t} \gamma^{i} r_{C}(i)-V_{C}(s), $ |
其中:r(i)、rC(i)分别代表i时刻主目标和约束的瞬时奖励值;γi代表折损系数。用υ表示AC框架中critic网络的参数,则υ的更新公式为
| $ \upsilon={clip}\left(v+\eta_{3}\left(\frac{\partial A_{\pi_{\theta}}}{\partial \upsilon}+\frac{\partial A_{C, \pi_{\theta}}}{\partial \upsilon}\right)\right)。$ | (6) |
算法1 动态优先级受限算法
输入:主目标和约束项对应的约束值α1、α2;λ、θ、υ更新对应的学习率;初始化参数λ0、θ0、υ0;每一个episode的时间长度T;训练的episode个数NUM_EPISODE。
输出:符合约束的最优策略πθ。
1) R, R_c=[ ];
2) InitializeEnv( );
3) CreateActorNetwork( );
4) CreateCriticNetwork( );
5) For i_episode in range(0, NUM_EPISODE):
6) For i_step in range(0, episode):
7) s ←env.observation( );
8) a ←Actor.select_action(state);
9) Next_state, reward, c_reward←env.step(a);
10) R←R+[reward], R_c←R_c+[c_reward];
11) ret, ret_c ←CalRet(R, R_c);
12) v, v_c←Critic(state);
13) ad, ad_c←ret-v, ret_c-v_c;
14) Update_Actor(ad, ad_c);
15) Update_Critic(ad, ad_c);
16) i_step←i_step+1;
17) End For
18) update_lamda(R, R_c, λ);
19) i_episode=i_episode+1;
20) End For
2.3 收敛性分析由于AC算法本身属于随机策略[23],式(4)~(6)的每一步都会伴随一定的误差,所以可以重新表述为
| $ \theta={clip}\left(\theta+\eta_{2} \nabla_{\theta} L+M_{\theta}\right), $ | (7) |
| $ \lambda={clip}\left(\lambda+\eta_{1} \nabla_{\lambda} L+M_{\lambda}\right), $ | (8) |
| $ \upsilon={clip}\left(v+\eta_{3}\left(\frac{\partial A_{\pi_{\theta}}}{\partial \upsilon}+\frac{\partial A_{C, \pi_{\theta}}}{\partial \upsilon}\right)+M_{\upsilon}\right), $ | (9) |
其中:Mθ、Mλ与Mυ分别代表每一个式子中的误差以及环境中的噪声项。
式(7)~(9)可看作微分方程(10)的估计策略,
| $ \dot{\theta}=\nabla_{\theta} L ; \dot{\lambda}=\nabla_{\lambda} L ; \dot{\upsilon}=\nabla_{\upsilon} L, $ | (10) |
导数项为0的点对应式(1)的极值点。在一定的前提条件下,基于式(7)~(9)的算法1能够收敛到一个符合约束的可行解。
假设1 式(1)的极值点或平衡点构成的集合非空,并且每个极值点或者平衡点都为近似的可行解。
假设2
假设3 式(7)~(9)迭代过程中每一步所积累的{Mθ}、{Mλ}与{Mυ}构成了鞅序列,即E(Mθ, Mλ, Mυ)=0。
假设4 在迭代过程中λ、θ、υ的值保持有界。
定理1 微分方程(10)是适定的,即对于任意θ0、λ0、υ0,式(10)都有解,且方程的轨迹收敛于平衡点。
证明 根据假设2,迭代公式的更新项是Lipschitz连续的,根据微分方程理论[13],式(10)是适定的。又根据假设4,λ、θ、υ的值保持有界,因此三者的轨迹在一个有界的区域内摆动,在摆动过程中必定会经过平衡点,并最终收敛。
定理2 在另外两个变量保持不变的前提下,式(7)~(9)每一步迭代构成的{λn}、{θn}、{υn}分别循迹于微分方程(10)。
证明 对于λ,在θ和υ保持不变的情况下,构造线性插值函数为
| $ \bar{\lambda}(t)=\lambda_{n}+\left(\lambda_{n+1}-\lambda_{n}\right) \frac{t-t(n)}{t(n+1)-t(n)}, $ |
可得
| $ \lim \limits_{s \rightarrow \infty} \sup \limits_{t \in[s, s+T]}\|\bar{\lambda}(t)-\lambda(t)\|=0 。$ |
即迭代公式所对应的插值函数会最终逼近微分方程对应的函数[24],θ与υ同理。
定理3 若η1、η2、η3都满足
证明 因为η3的值最大,所以式(9)相对于式(7)、(8)来说收敛得更快,所以在每一步的迭代过程中,式(8)、(9)都将υ作为一个接近平稳变化的量。而对于υ来说,式(7)、(8)每次更新的幅度更小,可以近似认为λ与θ的值保持不变。同理可以推出在每一个变量迭代过程中,都可以近似认为另外两个变量保持不变,因此符合定理2的前提条件。
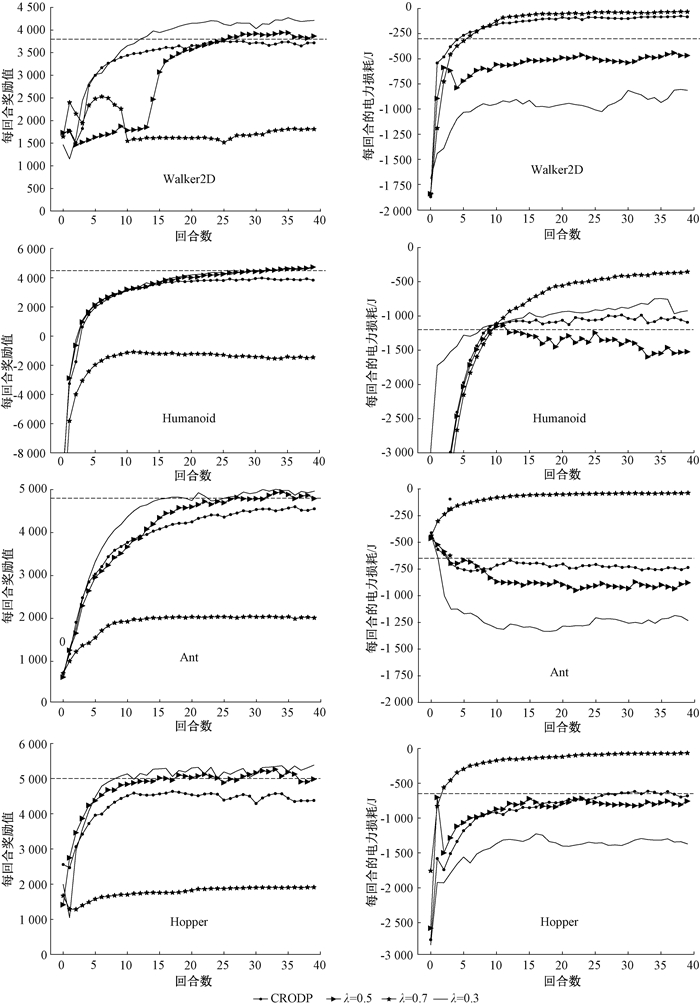
3 实验与结果 3.1 实验平台在基于PyBullet的机器人平台上测试本算法,测试的4个机器人环境分别为:Ant、Humanoid、Hopper以及Walker2D。智能体需要控制4种不同形态的机器人,每种机器人都由不同数量的关节组成,智能体需要在每个时间步决定作用在各个关节上的扭矩以实现机器人的正常行走。在每个时间步智能体的状态包含智能体重心的位置(若重心过低则认为机器人已经跌倒),各个关节之间的角度、角速度和机器人的行进方向以及行进速度。在训练过程中,智能体接受机器人当前的状态,并根据神经网络的参数决定施加在机器人各个关节上的扭矩来对机器人进行控制。机器人所涉及的目标包括保持平稳、靠近目的地、降低电力损耗、防止关节相互碰撞等。算法的学习目的即获得合适的神经网络参数,使得智能体在各种状态下选择能够满足上述目标的动作。基于平台上的比较结果见图 1。
|
图 1 机器人平台上CROPD与奖励塑造方法的比较 Fig. 1 Performance comparison of CRODP with reward shaping on Robotics |
在机器人实验平台中,智能体的主要目标为控制机器人的正常行走,同时实验环境也给每个关节动作给出了电力损耗,机器人每次活动的电力损耗为各个关节的电力损耗值之和,因此将机器人行走时的电力损耗值作为一个约束。根据各个机器人的构造,其电力损耗的约束值如表 1所示。
|
|
表 1 机器人的电力损耗约束 Tab. 1 Electronic constraints of robots |
选取电力损耗作为约束的原因是对于机器人来说,电力损耗与主要目标之间是相互冲突的,即行走的距离越长,电力损耗越高。约束算法需要同时兼顾行走目标与电力损耗,即要使电力损耗符合约束值,又要使机器人能够正常行走,若算法过于偏向降低电力损耗,则有可能使得机器人无法正常行走。
3.3 参数设置本文将提出的算法与基于奖励塑造的算法进行比较,奖励塑造算法固定了主目标与电力损耗之间的权重λ。本文中令λ=0.3,λ=0.5,λ=0.7,分别代表主目标优先模式、默认模式、约束优先模式。本文中的算法都基于PPO,其中actor网络与critic网络的架构相同,都由一个输入层、一个64×64的全连接层、一个输出层构成。算法的其他参数设置为η1=1×10-7,η2=1×10-6,η3=1×10-4;情节数量T=2 000,每个情节的时间步数H=2 048;每个算法的实验次数N=20;实验的软件环境为Ubuntu16.0,python版本为3.7,实验硬件为Nvidia 2080s。
3.4 结果分析根据图 1可知,在所有的4个环境中,本文提出的CROPD算法都找到了一个符合约束的近似可行解,即电力损耗值在约束线(图中的虚线对应于表 1)附近,并且除了Walker2D环境,都能够使机器人正常行走。机器人正常行走的含义是电力损耗值处在一个合理的数值区间,若电力损耗值过于接近0以及主目标的奖励值过低,则说明机器人无法正常移动。从曲线图中可知,默认模式和主目标优先模式奖励对应的算法都没有给出一个可行策略,即机器人的电力损耗超过了给定的约束值。另一方面,约束优先模式奖励对应的算法由于约束过高,使得损耗值接近0而主目标值过低,这意味着机器人无法正常行走。从实验结果还可以看出,奖励塑造算法只能抽象地规定主目标与约束间的权重而无法满足具体数值约束的要求。即使同一个权重,不同的机器人会表现出不同的行为。例如在Humanoid环境中,默认模式和主目标优先模式奖励对应的奖励值与约束值并没有区别。因此,本文提出的算法能够根据具体的约束值要求学习到一个合适的λ值。
4 结论本文提出的CRODP算法是基于CMDP的动态调整约束与奖励之间的优先级来实现受限强化学习的算法。实验证明,相比于预先规定约束与奖励之间的权重,本文提出的算法能够更好地满足不同环境下对于约束的具体要求,即在满足约束的条件下保证智能体的正常运行,尤其是在奖励与约束相互冲突的情况下。未来的工作计划将一个约束扩展到多个约束,使得智能体能够在不同环境中自动学习不同约束之间以及约束与奖励之间的权重。
| [1] |
JANG H C, HUANG Y C, CHIU H A. A study on the effectiveness of A2C and A3C reinforcement learning in parking space search in urban areas problem[C]//2020 International Conference on Information and Communication Technology Convergence. Piscataway: IEEE Press, 2020: 567-571.
(  0) 0) |
| [2] |
ZHANG T, XIAO M, ZOU Y, et al. Robotic constant-force grinding control with a press-and-release model and model-based reinforcement learning[J]. The international journal of advanced manufacturing technology, 2020, 106(1/2): 589-602. DOI:10.1007/s00170-019-04614-0 (  0) 0) |
| [3] |
CHEN W T, HU Z H. Using evolutionary game theory to study governments and manufacturers' behavioral strategies under various carbon taxes and subsidies[J]. Journal of cleaner production, 2018, 201: 123-141. DOI:10.1016/j.jclepro.2018.08.007 (  0) 0) |
| [4] |
ZHANG H J, QU C, ZHANG J D, et al. Self-adaptive priority correction for prioritized experience replay[J]. Applied sciences, 2020, 10(19): 6925. DOI:10.3390/app10196925 (  0) 0) |
| [5] |
BEKTAS T, EHMKE J F, PSARAFTIS H N, et al. The role of operational research in green freight transportation[J]. European journal of operational research, 2019, 274(3): 807-823. DOI:10.1016/j.ejor.2018.06.001 (  0) 0) |
| [6] |
何远, 张玉清, 张光华. 基于黑盒遗传算法的Android驱动漏洞挖掘[J]. 计算机学报, 2017, 40(5): 1031-1043. HE Y, ZHANG Y Q, ZHANG G H. Android driver vulnerability discovery based on black-box genetic algorithm[J]. Chinese journal of computers, 2017, 40(5): 1031-1043. (  0) 0) |
| [7] |
王琼, 郭戈. 车队速度滚动时域动态规划及非线性控制[J]. 自动化学报, 2019, 45(5): 888-896. WANG Q, GUO G. Platoon speed receding horizon dynamic programming and nonlinear control[J]. Acta automatica sinica, 2019, 45(5): 888-896. (  0) 0) |
| [8] |
GARCÍA J, SHAFIE D. Teaching a humanoid robot to walk faster through safe reinforcement learning[J]. Engineering applications of artificial intelligence, 2020, 88: 103360. DOI:10.1016/j.engappai.2019.103360 (  0) 0) |
| [9] |
ZHOU J Y, HE R X, WANG Y, et al. Autonomous driving trajectory optimization with dual-loop iterative anchoring path smoothing and piecewise-jerk speed optimization[J]. IEEE robotics and automation letters, 2021, 6(2): 439-446. DOI:10.1109/LRA.2020.3045925 (  0) 0) |
| [10] |
HUNDT A, KILLEEN B, GREENE N, et al. "good robot!": efficient reinforcement learning for multi-step visual tasks with sim to real transfer[J]. IEEE robotics and automation letters, 2020, 5(4): 6724-6731. DOI:10.1109/LRA.2020.3015448 (  0) 0) |
| [11] |
SAAD A, DONG Z, BUCKHAM B, et al. A new kriging-bat algorithm for solving computationally expensive black-box global optimization problems[J]. Engineering optimization, 2019, 51(2): 265-285. DOI:10.1080/0305215X.2018.1461853 (  0) 0) |
| [12] |
XU J, GUO C C. Optimal mode selection in D2D communication with deadline constraint: a CMDP perspective[J]. IEEE wireless communications letters, 2020, 9(8): 1245-1248. DOI:10.1109/LWC.2020.2986759 (  0) 0) |
| [13] |
SCHRITTWIESER J, ANTONOGLOU I, HUBERT T, et al. Mastering Atari, Go, chess and Shogi by planning with a learned model[J]. Nature, 2020, 588(7839): 604-609. DOI:10.1038/s41586-020-03051-4 (  0) 0) |
| [14] |
PAJARINEN J, THAI H L, AKROUR R, et al. Compatible natural gradient policy search[J]. Machine learning, 2019, 108(8/9): 1443-1466. (  0) 0) |
| [15] |
FENG C, SUN M C, ZHANG J. Reinforced deterministic and probabilistic load forecasting via Q-learning dynamic model selection[J]. IEEE transactions on smart grid, 2020, 11(2): 1377-1386. DOI:10.1109/TSG.2019.2937338 (  0) 0) |
| [16] |
FU Q M, HU L Y, WU H J, et al. A Sarsa-based adaptive controller for building energy conservation[J]. Journal of computational methods in sciences and engineering, 2018, 18(2): 329-338. DOI:10.3233/JCM-180792 (  0) 0) |
| [17] |
SHI H, XU M H, LI R. Deep learning for household load forecasting—a novel pooling deep RNN[J]. IEEE transactions on smart grid, 2018, 9(5): 5271-5280. DOI:10.1109/TSG.2017.2686012 (  0) 0) |
| [18] |
PAN J, WANG X S, CHENG Y H, et al. Multisource transfer double DQN based on actor learning[J]. IEEE transactions on neural networks and learning systems, 2018, 29(6): 2227-2238. DOI:10.1109/TNNLS.2018.2806087 (  0) 0) |
| [19] |
SEWAK M. Deep Q network (DQN), double DQN, and dueling DQN[M]. Singapore: Springer Singapore Press, 2019.
(  0) 0) |
| [20] |
BAN T W. An autonomous transmission scheme using dueling DQN for D2D communication networks[J]. IEEE transactions on vehicular technology, 2020, 69(12): 16348-16352. DOI:10.1109/TVT.2020.3041458 (  0) 0) |
| [21] |
SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550(7676): 354-359. DOI:10.1038/nature24270 (  0) 0) |
| [22] |
BRIZARD A J. An introduction to Lagrangian mechanics[M]. Singapore: World Scientific Press, 2015.
(  0) 0) |
| [23] |
ZHU J Y, SPALL J C. Stochastic approximation with nondecaying gain: error bound and data-driven gain-tuning[J]. International journal of robust and nonlinear control, 2020, 30(15): 5820-5870. DOI:10.1002/rnc.5151 (  0) 0) |
| [24] |
HATTORI H. Partial differential equations[M]. Singapore: World Scientific Press, 2019.
(  0) 0) |
 2022, Vol. 54
2022, Vol. 54


