2. 河北工业大学 经济管理学院 天津 300401
2. School of Economics and Management, Hebei University of Technology, Tianjin 300401, China
在如今的大数据时代,分析隐藏在数据背后的信息、规律成为一个重要的挑战,众多学者从多角度对大数据进行研究,产生了一系列的分析方法,其中最为经典的方法就是数据挖掘[1]。序列模式挖掘[2-3]作为数据挖掘领域中的一个重要课题,主要目的是从序列数据集中挖掘出用户感兴趣的子序列,通过分析潜在的模式帮助人们理解数据并进行决策。目前已经应用到多个领域,例如生物医学[4]、疾病检测[5]、物联网网络安全防范[6]和网络点击流分析[7-8]等。为了解决不同的问题,序列模式挖掘衍生出多种挖掘方法:为避免频繁但存在缺失项的模式丢失,Dong等[9]提出了负序列模式挖掘;为了更加灵活地挖掘满足特定要求的模式,Wang等[10]提出基于周期约束的序列模式挖掘方法;为了避免参数设置不合理,Wu等[11]提出了自适应间隙的序列模式挖掘。
然而现有的序列模式挖掘方法大多针对字符序列,由于时间序列具有高维性和连续性的特点[12-13],很难直接应用到时间序列分析中,因此,研究人员提出了新的研究方法。比如,在最初的研究中,通常会把原始的时间序列转化为其他域的数据来进行降维。最常用的方法有分段化表示法[14]、符号化表示法[15]等,但这些方法需要人为设定参数,过程中容易丢失重要的信息,并在一定程度上破坏了时间序列的连续性。同时,对于时间序列数据,如果过度关注元素数据的大小,很容易忽视序列的形态变化,难以发现有价值的信息。Wu等[16]提出了保序序列模式挖掘(OPP-Miner)算法挖掘序列中频繁出现的趋势变化。该方法使用模式的相对顺序表示其形状特征,称为保序模式,采用模式匹配[17]的方法计算支持度,需要多遍扫描原序列,从而在计算效率方面有待进一步提高,寻求高效的挖掘算法解决时间序列问题成为当前的挑战之一。
1 相关工作序列模式挖掘是数据挖掘领域的一个重要的分支,有广阔的应用前景。传统的序列模式挖掘问题是从序列数据库中找出频繁出现的模式[18],为了应对场景的需要,研究人员采取了在此基础上增加条件的方法,如Wu等[19]提出了高平均效用的序列模式挖掘;Wang等[20]提出了对比序列模式挖掘来提高分类的精度;武优西等[21]提出基于周期性一般间隙约束的序列模式挖掘方法。
尽管上述研究取得了良好的挖掘效果,但这些研究主要是针对符号化的序列或字符序列进行挖掘。上述方法难以应用到有序的连续数值构成的时间序列上进行挖掘,需要通过一系列转换,将原始的数值型数据转换成为其他域的数据,然后再进行挖掘。常见的方法有基于分段的表示和基于符号的表示,如Lin等[22]采用PAA方法将时间序列进行分段并每段求平均值,然后再挖掘其中的频繁模式;Tan等[23]根据数据波动将数字时间序列转换为字符型序列,并运用在具有弱通配符间隙的模式挖掘中。
虽然上述方法可以处理时间序列数据,但忽略了序列的原始特征,不易发现数据的变化趋势。为此,提出了基于次序关系的表示方法,如Kim等[24]提出KMP算法,寻找序列中出现趋势相同的子序列。在一些允许一定数据噪声存在的场景下,保序模式的近似匹配也相继被提出,如文献[25]提出的基于(δ, γ)距离的相似度度量方法,采用局部-整体约束,提高了匹配的精确度。随着研究的深入,保序模式匹配已经不能满足需要,Wu等[16]提出的OPP-Miner采用模式匹配的方式计算支持度。本文提出的RSMM利用子模式的结果得到超模式的支持度,避免了多次读取原序列,提高了挖掘效率。
2 相关定义定义1 (时间序列) 时间序列是指将同一统计指标的数值按照其发生的时间先后顺序排列而成的数列,可以表示为T=(t1, …, ti, …, tn)(1≤i≤n),其中n表示的是序列T的长度。
定义2 (秩) 元素pj在长度为m的模式P=(p1, …, pj, …pm)(1≤j≤m)中的秩记作rank(pj),表示的是pj在该模式中的相对大小。
定义3 (保序模式) 由元素的相对顺序表示的模式称为保序模式,记作rn(P)=(rank(p1), rank(p2), …, rank(pm)),模式中元素的个数即为模式的长度。
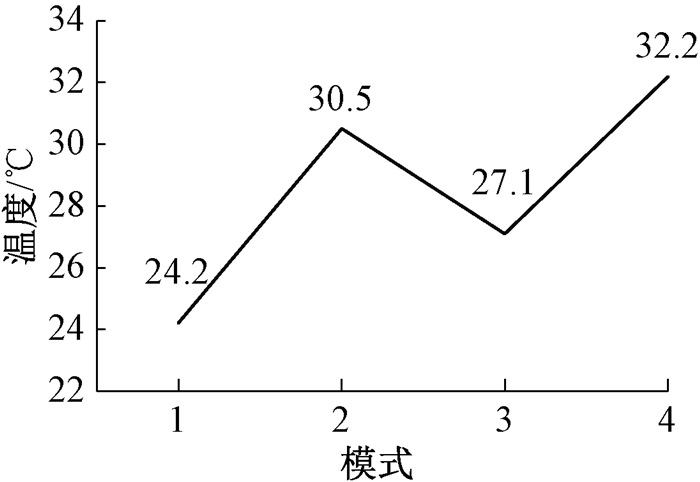
例1 给定温度模式(24.2, 30.5, 27.1, 32.2),由于元素24.2是子序列中最小的,因此rank(24.2)=1。同理可知,rank(30.5)=3。进而,其保序模式为(1, 3, 2, 4),其对应的趋势如图 1所示。
|
图 1 模式(1, 3, 2, 4) Fig. 1 Pattern (1, 3, 2, 4) |
定义4 (出现和支持度) 给定模式P=(p1, p2, …, pm),时间序列T=(t1, t2, …, tn),若存在子序列T′=(ti, ti+1, …, ti+m-1),1≤i,(i+m-1)≤n且rank(T′)=rank(P),则T′是模式P在序列T中的一次出现,记作〈ti+m-1〉。模式P在序列T中出现的总次数就是模式P在序列T中的支持度,记作sup(P)。
定义5 (频繁保序模式) 给定最小支持度阈值minsup,如果模式P在序列T中的支持度不小于给定的最小值支持度阈值minsup,则模式P称为频繁保序模式。
定义6 (保序模式挖掘) 给定时间序列T=(t1, t2, …, tn),最小支持度阈值minsup,挖掘出满足最小支持度阈值的所有频繁保序模式称为保序模式挖掘。
3 保序模式挖掘算法 3.1 候选模式生成传统的候选模式生成多采用枚举法,但该方法会产生大量冗余候选,为减少候选模式生成,采用模式融合方式。下面进行详细说明。
P和Q是长度为m的子模式,R和H是长度为m+1的超模式,LX是模式X在序列T中的匹配集合,其中元素lxi是X在序列中的一次出现。
定义7 (前缀、后缀保序模式、子模式和超模式) 给定模式P,子序列E=rn(p1, p2, …, pm-1)称为模式P的前缀保序模式,记作E=prefix(P);子序列K=rn(p2, p3, …, pm)称为模式P的后缀保序模式,记作K=suffix(P),其中:E和K是P的子模式;P是E和K的超模式。
定义8 (模式融合) 两个m长度的保序模式P、Q,若rn(suffix(P))=rn(prefix(Q)),那么模式P和Q可以生成(m+1)长度的超模式。这里存在两种情况。
情况1 若p1
① p1<qm:其中r1=p1,若qi<p1,则ri+1=qi;若qi≥p1,则ri+1=qi+1,1≤i≤m。
② p1>qm:其中r1=p1+1,若qi≤p1,则ri+1=qi;若qi>p1,则ri+1=qi+1,1≤i≤m。
情况2 若p1=qm,那么模式P和Q可以生成两个(m+1)长度的模式R、H,即R,H=P⊕Q。
其中:r1=hm+1=p1,rm+1=h1=p1+1,若qi<p1,则ri+1=qi;若qi>p1,则ri+1=qi+1,1≤i≤m-1。
例2 给定3长度的模式P=(2, 1, 3),Q=(1, 3, 2),可以生成4长度的候选模式。表 1给出了采用枚举法和模式融合生成的候选模式集。若采用枚举法,则每个模式都存在4种情况,以(2, 1, 3)为例,将1、2、3、4分别插在尾部,同时还要保持模式(2, 1, 3)的相对顺序,得到的候选模式如表 1所示。模式融合以(2, 1, 3)与(1, 3, 2)为例,因为p1=q3=2,满足情况2,进而可以产生2个候选模式(3, 1, 4, 2)、(2, 1, 4, 3)。从表 1可以看出,采用模式融合可以减少候选模式数量。
|
|
表 1 候选模式集 Tab. 1 Candidate pattern sets |
算法1 模式融合(pattern fusion,PF)
输入:子模式P, Q
输出:超模式R, H
1. E←rn(prefix(P))
2. K←rn(suffix(Q))
3. IF K==E
4. IF P[0]==Q[m-1]
5. R∪H←Fm[i]⊕Fm[j]
6. ELSE
7. R←Fm[i]⊕Fm[j]
8. END IF
9. END IF
10. RETURN R, H
3.2 支持度计算依据3.1可以看出,P⊕Q生成超模式有两种情况,下面分别介绍。
P和Q为m长度的模式,P为前缀保序模式,其对应的匹配集合为LP,Q为后缀保序模式,其对应的匹配集合为LQ。〈lpi〉为P的一次出现,即lpi∈LP;〈lqj〉为Q的一次出现,即lqj∈LQ。
方法1 R=P⊕Q:当且仅当lqj=lpi+1,〈lqj〉为R的一次出现,即lqj∈LR。
方法2 R、H=P⊕Q:当且仅当lqj=lpi+1时,〈lqj〉可能为R或H的一次出现,需要判断序列T中ta和tb的大小(a=lqj-m,b=lqj)。若ta<tb,〈lqj〉为R的一次出现,即lqj∈LR;若ta>tb,〈lqj〉为H的一次出现,即lqj∈LH;若ta=tb,〈lqj〉既不是R又不是H的出现。
最终集合LR、LH中元素的个数为超模式R、H的支持度,即sup(R)=|LR|,sup(H)=|LH|。
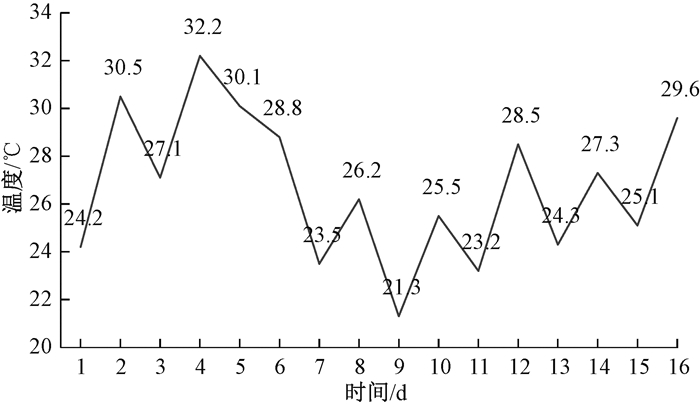
例3 图 2表示的是某地16天内的平均温度变化情况,2长度模式P=(1, 2)和Q=(2, 1)的匹配集合分别为LP={2, 4, 8, 10, 12, 14, 16}和LQ={3, 5, 6, 7, 9, 11, 13, 15}。
|
图 2 某地16天平均温度变化情况图 Fig. 2 The average temperature in 16 days |
P⊕Q生成两个超模式R=(1, 3, 2)和H=(2, 3, 1),P和Q分别为前缀保序模式和后缀保序模式。由于2∈LP且(2+1=3)∈LQ,根据方法2知,〈3〉可能为R或H的一次出现,可得a=3-2=1,b=3,由于t1<t3,所以〈3〉为R的一次出现,即3∈LR。同理可以得到R的匹配集合LR={3, 5, 11, 13, 15},sup(R)=5。H的匹配集合LH={9},sup(H)=1。接着G=Q⊕Q=(3, 2, 1),Q既为前缀保序模式又为后缀保序模式。根据方法1可知,〈6〉为G的一次出现,最终得到G的匹配集合LG={6, 7},sup(G)=2。
算法2 支持度计算算法(support calculation,SC)
输入:模式P和Q分别作为前缀模式和后缀模式的匹配集合LP,LQ
输出:超模式的支持度
1. LR={}; LH={}
2. IF P[0]==Q[m-1]
3. 根据方法2得到匹配集合LR和LH
4. ELSE
5. 根据方法1得到匹配集合LR
6. END IF
7. RETURN LR.size, LH.size
3.3 保序快速挖掘算法本节提出了一种保序快速挖掘算法,即读取子模式匹配结果挖掘(read sub-pattern matching for mining,RSMM)算法,具体步骤如下所示。
步骤1 扫描序列T,分别记录模式(1, 2),(2, 1)的匹配集合,计算模式的支持度,若为频繁模式,将该模式加入频繁集F2中;
步骤2 根据PF由频繁集Fm生成(m+1)长度的候选模式;
步骤3 利用SC计算候选模式的支持度,判断是否是频繁模式,若为频繁模式,将该模式加入频繁集Fm+1中;
步骤4 重复步骤2、3直到没有(m+1)长度的候选模式生成;
步骤5 依据Fm+1重复步骤2~4,直到没有候选模式生成。最终,集合F中的模式即为频繁保序模式。
例4 对于例3采用该算法挖掘频繁保序模式,首先扫描时间序列,得到模式P1=(1, 2)和P2=(2, 1)的匹配集合LP1={2, 4, 8, 10, 12, 14, 16},LP2={3, 5, 6, 7, 9, 11, 13, 15},因此sup(P1)=7,sup(P2)=8,由于minsup=3,可知F2={(1, 2), (2, 1)}。依据模式融合,(1, 2)⊕(2, 1)可以生成R=(1, 3, 2)和H=(2, 3, 1),根据计算支持度的方法可知sup(R)=5,sup(H)=1。得到3长度的频繁模式集F3={(1, 3, 2), (2, 1, 3), (3, 1, 2)}。以此类推,依据F3可以计算出4长度的频繁模式。最终,得到频繁模式集F={(1, 2), (2, 1), (1, 3, 2), (2, 1, 3), (3, 1, 2), (1, 3, 2, 4)}。
采用RSMM算法只在计算2长度模式时遍历时间序列,相比OPP-Miner减少了遍历序列的次数,提高了挖掘的效率。
算法3 RSMM
输入:序列数据集T, 最小支持度阈值minsup
输出:频繁模式集合F
1. 扫描序列T, 将模式(1, 2)、(2, 1)的匹配结果分别放入集合LP、LQ, 计算模式的支持度, 将频繁模式放入F2
2. m←2
3. WHILE Fm! =null DO
4. FOR each P in Fm DO
5. FOR each Q in Fm DO
6. 根据PF生成超模式
7. 采用SC计算超模式的支持度sup
8. IF sup≥minsup THEN
9. 将模式加入到频繁模式集Fm+1中
10. END IF
11. END FOR
12. END FOR
13. m←m+1;
14. END WHILE
15. RETURN F
定理1 采用RSMM计算模式支持度的方法是完备的。
证明 (反证法)存在子序列T′=(ti, ti+1, …, ti+m),若R=P⊕Q且rn(T′)=R,假设(i+m)
定理2 RSMM满足Apriori性质。
证明 给定序列T,若R=P⊕Q且R为频繁模式,即sup(R)≥minsup,依据定理1可知|LP|≥|LR|,即sup(P)≥sup(R),所以sup(P)≥minsup,同理,sup(Q)≥minsup。因此,该算法中频繁超模式的非空子模式也是频繁模式,即该算法满足Apriori性质。
定理3 保序快速挖掘算法的空间复杂度为O(L×(m+n)),时间复杂度为O(L×(L+n))。其中m、n、L分别为最长模式长度、序列长度和生成超模式的个数。
证明 该算法的空间复杂度由两部分组成:存储频繁模式空间和模式末位索引空间。由于频繁模式的个数为L,因此存储频繁模式空间复杂度为O(L×m);对于一个模式,产生的匹配集合空间为O(n),L个频繁模式,模式匹配集合空间复杂度为 O(L×n)。因此,该算法空间复杂度为O(L×(m+n))。在生成超模式时所需要的时间复杂度为O(L×L),在计算支持度阶段所需要的时间复杂度为O(n×L)。因此,该算法的时间复杂度为O(L×(L+n))。
4 实验部分 4.1 数据集本文采用真实数据集作为测试序列,股票和石油数据集来自https://www.yahoo.com/;天气数据集来自https://archive.ics.uci.edu/ml/datasets.php。其中T3~T5是截取T6的部分数据。具体数据集描述如表 2所示。
|
|
表 2 时间序列数据集 Tab. 2 Time series data sets |
实验运行的环境为Inter(R)Core(TM)i5-8265U处理器,主频1.60 GHz,内存8 GB,Windows 10,64位操作系统的计算机,程序的开发环境为Visual Studio 2019。
4.2 基线方法1) OPP-Miner:为了分析RSMM的效率,采用OPP-Miner作为对比算法;
2) RSMM-e:为了分析模式融合在生成超模式时的效果,提出了采用枚举策略的RSMM-e。
4.3 RSMM挖掘效果为了验证RSMM的效率,在T1、T2和T6上进行实验,设置minsup=12。挖掘出的频繁模式数量如表 3所示。
|
|
表 3 频繁模式数量 Tab. 3 Number of frequent patterns |
从表 3可以看出,在不同的数据集上,三种算法挖掘出的频繁模式个数是相同的,如在T1中,三种算法均挖掘出了160个频繁模式;在T6中,三种算法均挖掘出1 023个频繁模式。
接着,从运行时间和生成候选模式数量分析RSMM的挖掘效果。结果如表 4~5所示。
|
|
表 4 运行时间 Tab. 4 Running time |
|
|
表 5 候选模式数量 Tab. 5 The number of candidate patterns |
1) 采用RSMM可以提高挖掘的性能。在T6上,OPP-Miner需要1 594 ms而RSMM需要1 036 ms,运行时间缩短了558 ms。
2) 采用模式融合可以提高挖掘的性能。在T2上,RSMM-e生成5 738个候选模式,而RSMM采用模式融合生成了2 371个候选模式,减少了冗余模式的生成,从而将运行时间从18 156 ms减少到500 ms。
4.4 数据集长度对算法性能的影响为了验证数据集长度对挖掘效果的影响,我们在不同长度的数据集T3~T6上进行实验,从运行时间上分析算法的性能。minsup=100,实验结果如表 6所示。
|
|
表 6 运行时间 Tab. 6 Running time |
无论在长数据集还是短数据集上,RSMM的挖掘效果都是最好的,而对于长数据集,RSMM的挖掘效果更明显。从表 6可以看出,T3上,OPP-Miner需要16 ms,而RSMM需要15 ms;T6上,OPP-Miner需要250 ms,而RSMM需要125 ms,时间缩短了50%。可以看出,RSMM对长数据集有更优的效果。这是由于挖掘长数据集时,会产生更多的候选模式,OPP-Miner会多次扫描时间序列,浪费了不必要的时间,而采用RSMM可以避免多次扫描序列。因此,对于数据集效果更明显。
5 结论我们提出的RSMM算法在计算支持度时,通过子模式匹配结果计算超模式的支持度,避免了多次读取原序列。在时间序列数据集上的挖掘实验表明RSMM具有高效性,可以在更短的时间内挖掘到所有频繁出现的趋势,与OPP-Miner相比,在运行时间上平均减少了26%。并且对于长序列,RSMM的挖掘效果更明显,运行时间减少了50%。
| [1] |
WU X D, ZHU X Q, WU G Q, et al. Data mining with big data[J]. IEEE transactions on knowledge and data engineering, 2014, 26(1): 97-107. DOI:10.1109/TKDE.2013.109 (  0) 0) |
| [2] |
WU Y X, TONG Y, ZHU X Q, et al. NOSEP: nonoverlapping sequence pattern mining with gap constraints[J]. IEEE transactions on cybernetics, 2018, 48(10): 2809-2822. DOI:10.1109/TCYB.2017.2750691 (  0) 0) |
| [3] |
王乐, 王水, 刘胜蓝, 等. 基于索引树的带通配符序列模式挖掘算法[J]. 计算机学报, 2019, 42(3): 554-565. WANG L, WANG S, LIU S L, et al. An algorithm of mining sequential pattern with wildcards based on index-tree[J]. Chinese journal of computers, 2019, 42(3): 554-565. (  0) 0) |
| [4] |
WU Y X, ZHU C R, LI Y, et al. NetNCSP: Nonoverlapping closed sequential pattern mining[J]. Knowledge-based systems, 2020, 196: 105812. DOI:10.1016/j.knosys.2020.105812 (  0) 0) |
| [5] |
侯泳旭, 段磊, 李岭, 等. 基于疾病信息网络的表型相似基因搜索[J]. 软件学报, 2018, 29(3): 721-733. HOU Y X, DUAN L, LI L, et al. Search of genes with similar phenotype based on disease information network[J]. Journal of software, 2018, 29(3): 721-733. (  0) 0) |
| [6] |
CHEN X, XIAO R L, XIN D, et al. Constructing a novel spark-based distributed maximum frequent sequence pattern mining for IoTlog[C]//Proceedings of the 8th International Conference on Communication and Network Security. New York: ACM Press, 2018: 112-116.
(  0) 0) |
| [7] |
NISHIMURA N, SUKEGAWA N, TAKANO Y, et al. A latent-class model for estimating product-choice probabilities from clickstream data[J]. Information sciences, 2018, 429: 406-420. DOI:10.1016/j.ins.2017.11.014 (  0) 0) |
| [8] |
武守晓, 房俊. 面向高速乱序流的top-k连续查询方法[J]. 郑州大学学报(理学版), 2021, 53(3): 93-99. WU S X, FANG J. Continuous top-k query method over high-speed out-of-order data streams[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(3): 93-99. (  0) 0) |
| [9] |
DONG X J, GONG Y S, CAO L B. F-NSP+: a fast negative sequential patterns mining method with self-adaptive data storage[J]. Pattern recognition, 2018, 84: 13-27. DOI:10.1016/j.patcog.2018.06.016 (  0) 0) |
| [10] |
WANG W T, DUAN L, NUMMENMAA J, et al. Mining frequent closed sequential patterns with non-user-defined gap constraints[C]//Proceeding of the International Conference on Advanced Data Mining and Applications. Berlin: Springer Press, 2014: 57-70.
(  0) 0) |
| [11] |
WU Y X, WANG Y H, LI Y, et al. Top-k self-adaptive contrast sequential pattern mining[J]. IEEE transactions on cybernetics, 2021, 89: 89-97. (  0) 0) |
| [12] |
谭章禄, 王兆刚, 胡翰. 时间序列趋势相似性度量方法研究[J]. 计算机工程与应用, 2020, 56(10): 94-99. TAN Z L, WANG Z G, HU H. Research on trend similarity measurement method of time series[J]. Computer engineering and applications, 2020, 56(10): 94-99. DOI:10.3778/j.issn.1002-8331.1906-0352 (  0) 0) |
| [13] |
李靖, 任丽芳, 王文剑. 一种响应时间感知的移动服务组合方法[J]. 郑州大学学报(理学版), 2021, 53(3): 30-36. LI J, REN L F, WANG W J. A method for response time-aware mobile service composition[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(3): 30-36. (  0) 0) |
| [14] |
GUO C H, LI H L, PAN D H. An improved piecewise aggregate approximation based on statistical features for time series mining[C]//Proceeding of the Knowledge Science Engineering and Management. Berlin: Springer Press, 2010: 234-244.
(  0) 0) |
| [15] |
TAN C D, MIN F, WANG M, et al. Discovering patterns with weak-wildcard gaps[J]. IEEE access, 2016, 4: 4922-4932. DOI:10.1109/ACCESS.2016.2593953 (  0) 0) |
| [16] |
WU Y X, HU Q, LI Y, et al. OPP-Miner: order-preserving sequential pattern mining[J]. IEEE transactions on cybernetics, 2021, 5: 589-597. (  0) 0) |
| [17] |
武优西, 刘茜, 闫文杰, 等. 无重叠条件严格模式匹配的高效求解算法[J]. 软件学报, 2020, 23(7): 177-185. WU Y X, LIU X, YAN W J, et al. Efficient algorithm for non-overlapping strict sequential pattern matching[J]. Journal of software, 2020, 23(7): 177-185. (  0) 0) |
| [18] |
DONG X J, QIU P, LÜ J, et al. Mining top-k useful negative sequential patterns via learning[J]. IEEE transactions on neural networks andlearning systems, 2019, 30(9): 2764-2778. DOI:10.1109/TNNLS.2018.2886199 (  0) 0) |
| [19] |
WU Y X, LEI R, LI Y, et al. HAOP-Miner: self-adaptive high-average utility one-off sequential pattern mining[J]. Expert systems with applications, 2021, 184: 115449. DOI:10.1016/j.eswa.2021.115449 (  0) 0) |
| [20] |
WANG X M, DUAN L, DONG G Z, et al. Efficient mining of density-aware distinguishing sequential patterns with gap constraints[C]//Proceeding of the International Conference on Database Systems for Advanced Applications. Berlin: Springer Press, 2014: 372-387.
(  0) 0) |
| [21] |
武优西, 周坤, 刘靖宇, 等. 周期性一般间隙约束的序列模式挖掘[J]. 计算机学报, 2017, 40(6): 1338-1352. WU Y X, ZHOU K, LIU J Y, et al. Mining sequential patterns with periodic general gap constraints[J]. Chinese journal of computers, 2017, 40(6): 1338-1352. (  0) 0) |
| [22] |
LIN J, KEOGH E, LONARDI S, et al. Finding motifs in time series[C]//Proceeding of Workshop on Temporal Data Mining. Piscataway: IEEE Press, 2002: 53-68.
(  0) 0) |
| [23] |
TAN C D, MIN F, WANG M, et al. Discovering patterns with weak-wildcard gaps[J]. IEEE access, 2016, 4: 4922-4932. DOI:10.1109/ACCESS.2016.2593953 (  0) 0) |
| [24] |
KIM J, EADES P, FLEISCHER R, et al. Order-preserving matching[J]. Theoretical computer science, 2014, 525: 68-79. DOI:10.1016/j.tcs.2013.10.006 (  0) 0) |
| [25] |
MENDIVELSO J, NIQUEFA R, PINZÓN Y, et al. New algorithms for δ-order preserving matching[J]. Ingeniería, 2018, 23(2): 190-202. (  0) 0) |
 2022, Vol. 54
2022, Vol. 54


