2. 中山大学 数据科学与计算机学院 广东 广州 510275
2. School of Data Science and Computer Science, Sun Yat-Sen University, Guangzhou 510275, China
大气湍流中各点的压力、速度和温度等物理属性会随时空发生剧烈波动,从而引起折射率的随机波动,干扰入射光的相位,使图像产生几何畸变、运动模糊、重影、噪声等问题[1-3]。远距离成像系统的照片和视频质量易受到大气湍流的影响而下降,以至于无法分辨视频中物体的真实形状。为了消除大气湍流对图像序列的影响,研究者们提出了多种盲反卷积的方法,主要可分为3种:第1种是利用图像配准和图像融合思想从退化序列中恢复理想图像[4-6];第2种是利用稀疏表示的思想重建去模糊后的图像[7-9];第3种方法是使用各种先验思想计算出模糊核,如最大似然先验和超拉普拉斯先验等[10-11]。
文献[4]提出了一种从湍流退化序列中获得近衍射限图像(near diffraction limit, NDL)的方法,利用b样条插值、非刚性的图像配准和图像融合得到近衍射限图像,并使用盲反卷积恢复出高质量的图像。文献[6]提出了一种简单有效的帧选择方法,从退化序列中选择质量较高的帧,再从中选择退化感兴趣局部区域(region of interest, ROI)进行图像配准,采用基于二分树复数小波变换的局部融合方法来去除湍流扭曲。文献[12]使用了高效过滤流(efficient filter flow, EFF)方法,提出了一个比非刚性配准技术更快、更简单的空间变化盲反卷积框架,将线性变换(如模糊和非刚性变换)引入到湍流图像的成像过程中,计算局部点扩散函数(point spread function, PSF)。然而,线性变换同时也引入了一个不充分的先验条件,并不能完全去除湍流且容易产生振铃效应。文献[13]指出并不是图像序列中的每一帧都适合用来重建清晰图像,对图像序列进行选择和采样是非常必要的,并提出了一个不涉及图像配准的能量模型,通过对能量函数的迭代简化,完成图像序列的联合采样,并从中提取出清晰的图像。这种方法比NDL方法更有效,但同时对图像序列帧数量的要求也比NDL方法更高。
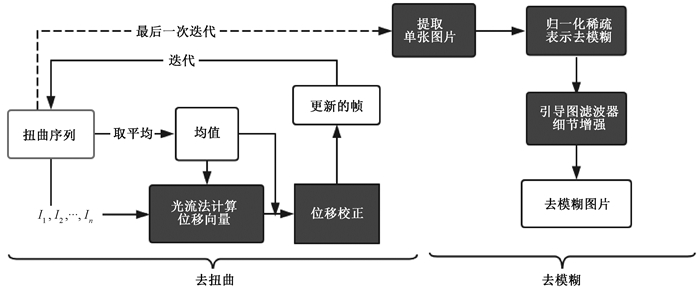
然而,上述大多数方法对模糊核的精度和视频序列帧的数量都有很高的要求,在实际情况中,有效序列帧的数量是十分有限的。我们提出了一种结合物理光流与细节增强的方法(算法流程图见图 1),将图像湍流影响的消除分为两步,首先采用物理光流方法[14]算出各序列帧与参考帧之间的位移信息,对各序列帧进行校正;然后利用归一化稀疏表示和引导图滤波器[15]进行盲反卷积和细节增强。物理光流方法能更加精确地计算出各序列帧与参考帧之间的运动矢量,提高几何校正的精度,降低对序列帧数量的要求,而细节增强则解决了图像的细节丢失问题。通过实验发现,一些对普通失真图像进行恢复的方法对大气湍流下的图像也有一定作用,文献[16]提出的一种对水下图像序列去扭曲的两阶段重建方法,文献[10]利用超拉普拉斯先验项来拟合自然场景中梯度的重尾分布(HLP),采用交替最小化方案对单张模糊图像进行恢复。
|
图 1 算法流程图 Fig. 1 Algorithm flow chart |
对于一个受湍流影响的视频序列中的每一帧I1、I2、…、In,大小为w×h,因为空气湍流的影响均有不同程度的失真。在本文中,使用序列的均值作为参考帧,用物理光流算法计算每一帧与均值之间的位移矢量u=(μ, v)T。光流法利用时域内不同图像帧之间像素点的变化和相关关系求出两张图像之间的像素位移和运动信息。本文在经典光流法(horn-schunck algorithm, H-S)[17]的基础上,使用了一种基于物理光流的优化方法[18-19]。经典的H-S算法的光流约束方程为
| $ \left[ {\frac{{\partial g}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla g} \right]\nabla g - \alpha {\nabla ^2}\mathit{\boldsymbol{u = }}0, $ |
式中:g表示图像亮度;u=(μ, ν)T代表光流;▽是梯度算子;α是平滑系数。
文献[19-20]利用透视投影变换将物体的空间坐标表示为图像坐标,从投影运动方程推导获得物理光流方程,同时考虑扩散项和边界项f,得到位移方程
| $ \frac{{\partial g}}{{\partial t}} + \nabla \left( {g\mathit{\boldsymbol{u}}} \right) = f, $ | (1) |
最小化式(1)的L2范数,得到位移矢量u=(μ, ν)T,μ和ν分别是像素点在水平方向和垂直方向的位移。对u=(μ, ν)T进行双线性插值操作优化后,得到校正位移矢量场U=(Ux, Uy)T,按照下式进行几何畸变的校正,
| $ {i_{new}}{\rm{ = }}i + {k_1}{{\rm{Y}}_x};{j_{new}} = j + {k_2}{U_y};{I_{new}}\left( {{i_{new}}, {j_{new}}} \right) = I\left( {i, j} \right), $ |
其中:(i, j)是像素点的坐标;k是权重系数。实验结果表明本文方法极大地降低了对有效视频帧数量的要求,只需要大约5帧就能得到相对理想的去扭曲结果,而之前的许多方法通常需要几十甚至几百帧图像序列来完成去扭曲。图 2展示了去扭曲阶段的实验结果,同时与文献[16]的方法进行了对比,从扭曲的墙壁纹理的变化可以看到,本文方法的去扭曲效果更优。

|
图 2 去扭曲结果比较 Fig. 2 Comparison of restoration effects |
由于大气湍流的时空可变和无规则特性,湍流影响下的图像模糊比普通的图像模糊要复杂得多,我们考虑大气湍流下模糊图像的成像模型为y=x⊗K+N,其中:y代表湍流下图像;x表示原始真值图像;K代表模糊核;N是图像噪声。近年来,稀疏表示成功地应用于图像去模糊,如归一化稀疏表示和行列稀疏表示[9]。L1范数是稀疏表示去模糊中最常用的稀疏正则化项,可通过快速迭代收缩阈值算法(fast iterative shrinkage-thresholding algorithm, FISTA)[21]最小化L1范数,解决L1正则化问题。图像被模糊时,中低频段图像能量几乎不受影响,而高频段图像能量被削弱,其高频段L1范数的值也随之降低,此时选择L1范数作为正则化项,对模糊核的约束性不够。为了保证稀疏约束性,在高频段使用L1范数和L2范数的比值作为稀疏正则化项[22],求解正则化代价函数得到模糊核k,再通过非盲反卷积获得去模糊图像P。
2.2 细节增强场景较复杂的图像在去扭曲和稀疏表示的过程中容易丢失细节,需要进一步增强图像中的细节。图像可以被建模为基础层和细节层的组合,引导图滤波器[15]能有效地保持图像边缘,使图像平滑,从而得到图像的基础层,利用原始图像与基础层之间的差值可得到细节层。引导图滤波器在像素点i的输出表达式为
| $ {q_i}{\rm{ = }}\sum\limits_j {{W_{ij}}} \left( g \right){p_j}。$ | (2) |
式(2)中Wij是关于滤波器引导图的函数,假设引导图和滤波器输出q在局部区域窗口内是线性相关的。因此, 我们可以假设在以k为中心的局部窗口中具有线性关系
| $ {q_i} = {a_k} \times g + {b_k}, \forall i \in {\omega _k}。$ | (3) |
其中(ak,bk)是线性相关系数,在局部窗口ωk中,(ak,bk)被看作常数。用线性脊回归模型求解式(3)的能量函数可计算出(ak,bk)的表达式,根据式(2)可得出滤波器的输出。但是,对于同一个像素点i,它可以属于多个ωk,从而产生多个不同的和qi。通常的解决办法是取平均值作为最终有效系数,在本文中,我们选择计算所有(ak,bk)的加权中值[22]作为最终有效系数,有效减少图像伪影。将属于不同ωk的每一组放在一个以s为中心的新矩阵R中,提取矩阵R局部图像结构(local graph structure,LGS)作为R的特征图谱f,则R的中心s点的加权值可表示为
| $ {W_{xs}} = h\left( {f\left( x \right)f\left( s \right)} \right), $ |
其中:f(x)和f(s)分别是特征图谱在x和s点的值;h是相邻像素之间的影响函数。计算R中每一元素的加权值并按升值排序,取中位数作为最终系数,则引导图滤波器输出可表示为qi=ai×gi+bi,在得到滤波器最终输出Ibase后,图像细节增强可通过Ienhanced=Ibase+τ(I-Ibase)得到,其中:τ是控制细节增强程度的系数;Ienhanced表示细节增强后图像。
3 实验本文算法在合成湍流序列和真实湍流序列上均做了充分的实验,验证了方法的有效性。图 3是在真实环境下拍摄得到的湍流图像,但真实湍流数据有限,且真实条件下获得的湍流图像,均没有所对应的原始数据(ground truth),这为算法的性能量化分析带来了困难。因此,我们发展了一种湍流图像的合成算法,能得到在不同湍流强度下的合成图像。图 4给出了本文所使用到的合成湍流图像,图 5给出了两个阶段的实验结果,图 6将本文方法与文献[4]所提出的DNL方法、文献[10]的超拉普拉斯先验(hyper-laplacian priors, HLP)方法进行了比较。

|
图 3 真实湍流图像 Fig. 3 Real turbulence images |

|
图 4 合成湍流图像 Fig. 4 Synthesize turbulence images |

|
图 5 本文方法去扭曲和细节增强效果图 Fig. 5 Distortion and detail enhancement using the proposed method |

|
图 6 不同方法的去湍流效果 Fig. 6 Deturbulence effects of different methods |
图 7对比了本文方法与IPR(internal patch recurrence, IPR)方法[23]在合成湍流图像上的效果,本文方法的恢复结果更接近于真值。我们采用平均结构相似性(mean structural similarity, MSSIM)来衡量去扭曲效果,MSSIM的取值范围为[0, 1],值越大说明图像与真值之间的差距越小,失真越少。MSSIM值计算公式为
| $ MSSIM = \frac{1}{N}\sum\limits_{k = 1}^N {SSIM\left( {{x_k}, {y_k}} \right)} ;SSIM\left( {x, y} \right) = L\left( {x, y} \right) * C\left( {x, y} \right) * S\left( {x, y} \right)。$ |

|
图 7 合成湍流图像的恢复效果 Fig. 7 The restoration effect of synthetic turbulence image |
表 1展示了本文和IPR方法[23]在合成湍流图像数据实验结果的MSSIM值,本文方法的表现明显优于IPR方法。从峰值信噪比(PSNR)来看,与DNL[4]和HLP[10]方法相比,本文方法能将PSNR平均提高3~3.5 dB,具体数据如表 2所示。
|
|
表 1 平均结构相似性比较 Tab. 1 Average structural similarity comparison |
|
|
表 2 PSNR值比较 Tab. 2 PSNR value comparison |
本文利用物理光流法计算序列帧与参考帧之间的位移差,通过校正位移差消除了图像中的几何畸变。物理光流法对像素位移差的计算更加准确,而且速度更快,极大地降低了对有效序列帧数量的要求。在本文的实验中,我们使用5~10帧湍流图像就可以恢复出清晰图像,而文献[4]的方法需要的帧数是本文的几十倍。在细节增强阶段,使用归一化稀疏表示进一步恢复图像,使用引导图滤波器对图像进行增强,使图像细节更加清晰,恢复效果更理想。
| [1] |
郑秋亚, 陈芳, 吕梦迪, 等. 两种湍流模型在跨声速绕流中的比较分析[J]. 郑州大学学报(理学版), 2019, 51(1): 84-88. ZHENG Q Y, CHEN F, LV M D, et al. Comparison and analysis of two turbulence models in transonic flow[J]. Journal of Zhengzhou university (natural science edition), 2019, 51(1): 84-88. (  0) 0) |
| [2] |
LI J S, ZHANG J, SUI Z S, et al. Restoration method based on low-rank decomposition for video under turbulence[C]//International Conference on Virtual Reality and Visualization. Xiamen, 2015: 68-71.
(  0) 0) |
| [3] |
GIBSON K B, NGUYEN T Q. An analysis and method for contrast enhancement turbulence mitigation[J]. IEEE transactions on image processing, 2014, 23(7): 3179-3190. DOI:10.1109/TIP.2014.2328180 (  0) 0) |
| [4] |
ZHU X, MILANFAR P. Removing atmospheric turbulence via space-invariant deconvolution[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(1): 157-170. DOI:10.1109/TPAMI.2012.82 (  0) 0) |
| [5] |
ANANTRASIRICHAI N, ACHIM A, KINGSBURY N G, et al. Atmospheric turbulence mitigation using complex wavelet-based fusion[J]. IEEE transactions on image processing, 2013, 22(6): 2398-2408. DOI:10.1109/TIP.2013.2249078 (  0) 0) |
| [6] |
AUBAILLY M, VORONTSOV M A, CARHART G W, et al. Automated video enhancement from a stream of atmospherically-distorted images: the lucky-region fusion approach[C]//Atmospheric Optics: Models, Measurements, and Target-in-the-Loop Propagation Ⅲ. International Society for Optics and Photonics, San Diego, 2009, 7463: 74630C.
(  0) 0) |
| [7] |
XU L, ZHENG S C, JIA J Y. Unnatural L0 sparse representation for natural image deblurring[C]//IEEE Conference on Computer Vision and Pattern Recognition. Portland, 2013: 1107-1114.
(  0) 0) |
| [8] |
洪汉玉, 张天序, 余国亮. 航天湍流退化图像的极大似然估计规整化复原算法[J]. 红外与毫米波学报, 2005, 24(2): 130-134. HONG H Y, ZHANG T X, YU G L. Regularized restoration algorithm of astronautcal turbulence-degraded images using maximum-likelihood estimation[J]. Journal infrared millimeter and waves, 2005, 24(2): 130-134. (  0) 0) |
| [9] |
TOFIGHI M, LI Y L, MONGA V. Blind image deblurring using row-column sparse representations[J]. IEEE signal processing letters, 2018, 25(2): 273-277. DOI:10.1109/LSP.2017.2782570 (  0) 0) |
| [10] |
KRISHNAN D, FERGUS R. Fast parameter estimation using Green's functions[M]. Cambridge: Massachusetts Institute of Technology, 2002.
(  0) 0) |
| [11] |
LEVIN A, WEISS Y, DURAND F, et al. Efficient marginal likelihood optimization in blind deconvolution[C]//IEEE Conference on Computer Vision and Pattern Recognition. Providence, 2011: 2657-2664.
(  0) 0) |
| [12] |
HIRSCH M, SRA S, SCHÖLKOPF B, et al. Efficient filter flow for space-variant multiframe blind deconvolution[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, 2010: 607-614.
(  0) 0) |
| [13] |
LAU C P, LAI Y H, LUI L M. Variational models for joint subsampling and reconstruction of turbulence-degraded images[J]. Journal of scientific computing, 2019, 78(3): 1488-1525. DOI:10.1007/s10915-018-0833-4 (  0) 0) |
| [14] |
WANG B, CAI Z M, SHEN L X, et al. An analysis of physics-based optical flow[J]. Journal of computational and applied mathematics, 2015, 276: 62-80. DOI:10.1016/j.cam.2014.08.020 (  0) 0) |
| [15] |
HE K M, SUN J, TANG X O. Guided image filtering[M]. Berlin: Springer, 2010: 1-14.
(  0) 0) |
| [16] |
OREIFEJ O, SHU G, PACE T, et al. A two-stage reconstruction approach for seeing through water[C]//IEEE Conference on Computer Vision and Pattern Recognition. Providence, 2011: 1153-1160.
(  0) 0) |
| [17] |
HORN B K P, SCHUNCK B G. Determining optical flow[J]. Artifical intelligence, 1981, 17(3): 185-203. (  0) 0) |
| [18] |
李蓉. 利用PSO估算Lucas-Kanade光流模型的参数[J]. 郑州大学学报(理学版), 2013, 45(3): 58-62. LI R. Estimation of Lucas-Kanade parameters using PSO[J]. Journal of Zhengzhou university (natural science edition), 2013, 45(3): 58-62. (  0) 0) |
| [19] |
NOMURA A, MIIKE H, KOGA K. Field theory approach for determining optical flow[J]. Pattern recognition letters, 1991, 12(3): 183-190. DOI:10.1016/0167-8655(91)90048-Q (  0) 0) |
| [20] |
MADJIDI H, NEGAHDARIPOUR S. On robustness and localization accuracy of optical flow computation for underwater color images[J]. Computer vision and image understanding, 2006, 104(1): 61-76. DOI:10.1016/j.cviu.2006.07.003 (  0) 0) |
| [21] |
ZHANG L L, XU G Q, XUE Q, et al. An iterative thresholding algorithm for the inverse problem of electrical resistance tomography[J]. Flow measurement and instrumentation, 2013, 33: 244-250. (  0) 0) |
| [22] |
KRISHNAN D, TAY T, FERGUS R. Blind deconvolution using a normalized sparsity measure[C]//IEEE Conference on Computer Vision and Pattern Recognition. Providence, 2011: 233-240.
(  0) 0) |
| [23] |
ZHANG Q, XU L, JIA J Y. 100+ times faster weighted median filter (WMF)[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus, 2014: 2830-2837.
(  0) 0) |
 2021, Vol. 53
2021, Vol. 53


