2. 农产品质量安全追溯技术河南省工程实验室 河南 周口 466001;
3. 郑州大学 互联网医疗与健康服务河南省协同创新中心 河南 郑州 450001;
4. 郑州大学 产业技术研究院 河南 郑州 450001
2. Traceability Technology of Agricultural Products Quality and Safety Engineering Laboratory of Henan Provincial, Zhoukou 466001, China;
3. Collaborative Innovation Center of Internet Medical and Healthcare in Henan, Zhengzhou 450001, China;
4. Institute of Industrial Technology, Zhengzhou University, Zhengzhou 450001, China
微博社交网络社区挖掘对于阻断网络谣言传播和舆情监测有重要作用,并且,对个性化服务推荐和广告精准投放等商业应用也有重要意义。近年来,社交网络社区划分方法的研究成为计算机领域比较热门的课题。Chouchani等[1]提出一种基于用户兴趣的社区挖掘方法,以兴趣为侧重点衡量用户关系、发现社区。Mahabadi等[2]设计一种标签传播算法,无须使用预先训练或符合特定要求的预定义特征,就能获得更好的加速比和半确定性结果。Liu等[3]推导出计算局部重叠模块化增量的新公式,可以准确而快速地找到重叠的社区,减少运算时间,并设计了一种新的相似度度量来减小孤立群体的影响。Kumar等[4]提出了一种基于双目标函数的重叠社区检测方法,运用两个目标函数分别实现最大化社区内部连接密度和最小化社区外部连接密度。Messaoudi等[5]将重叠社区检测问题转化为优化问题,并设计了一种新的优化算法来求解所建立的优化模型,提出了一种混合元启发式方法来检测网络中的重叠社区。Trivedi等[6]提出了一种基于容忍度邻域的混合计算方法来检测社交网络中的重叠社区, 成功将平面划分方法应用于社区挖掘。李政廉等[7]引入网络节点的社区连通度得分和邻域连通度得分,提出基于局部信息的快速重叠社区检测算法,能够挖掘出近似最优的社区,收获了低复杂度。Kumar等[8]设计了基于邻域邻近度的加权网络重叠社区结构检测算法,综合了相邻接点的邻近度和网络边的权重,更适合有权重区分的网络结构。Javed等[9]从传统到最新,回顾了当前流行的社区检测算法,重点介绍了基于非负矩阵分解等降维技术。Hajiabadi等[10]通过一个集成的框架来提取重叠和非重叠的社区结构,而不需要依赖于网络上的先验结构连通性。杜航原等[11]基于搜索密度峰值的聚类思想设计了一种网络节点的中心性度量模型,用网络节点的内聚度和分离度,分别描述网络社区内部连接稠密和外部连接稀疏的结构特征。闫涵等[12]和陈珂等[13]分别在微博用户兴趣度和文本情感分析的应用方面取得了较好的成果,对于社交网络社区挖掘有较高的参考价值。Newman[14]利用模块度衡量社区结构的质量,提出了基于贪心思想的快速算法,社区挖掘效果较好。Blondel等[15]提出了检测大型网络社区结构的方法,引入模块度增量决定节点的归属,并且每次迭代基于单节点的处理,能应用于大规模社交网络,减少时间开销,给本文的研究提供了启发。
1 重叠社区划分方法微博社交网络由用户作为网络节点,用户之间的关注关系作为网络连边,现实情况下,用户之间的关注关系具有方向性,所以,微博社交网络中的边为有向边,微博社交网络可以看成一个有向图D=〈V, E〉,其中:V是D中的节点集;E是有向边的集合,E中的每一个元素均是有序偶〈u, v〉。
1.1 链路结构微博社交媒体中,用户之间为关注或不关注关系,在构造的社交网络中,A关注B表示A到B存在一条有向边,并且此边无权重区别,所以,传统网络社区划分方法中,以边的权重来度量节点之间距离的方法不适用于微博社交网络。本文根据微博用户之间的关注关系构成的网络拓扑中链路结构紧密度来衡量节点之间关系的紧密度。在网络拓扑结构中,用户节点之间的关系又分为直接相邻和非直接相邻两种:如果x,y∈V,并且〈x,y〉∈E,则表示两者之间存在直接关注关系,关系相对紧密;如果x和y之间非直接相邻,则两者之间的关系紧密度相对较弱。用户节点x和y之间链路紧密度计算方法为
| $ lin{k_{xy}} = \left\{ {\begin{array}{*{20}{l}} {\left( {{d_{xy}} + {d_{yx}}} \right)/2, \;\;\;{\kern 1pt} x, y直接相邻, }\\ {{E_{xy}}/(n + 2)I{O_{xy}}, \;\;\;{\kern 1pt} x, y非直接相邻, } \end{array}} \right. $ | (1) |
式中:dxy表示节点x到y的入度,即x是否关注了y,如果x关注了y,则dxy=1,否则dxy=0;dyx表示节点y到x的入度,即y是否关注了x,如果y关注了x,则dyx=1,否则dyx=0;n表示节点x和y之间建立最短通路需要经过的结点个数,1/(n+2)是两者之间紧密度权重,建立最短通路需要经过的节点越多,两者关系越松散;Exy表示x和y之间建立最短通路所经过的边的数量,计算公式为
| $ {E_{xy}} = \sum\limits_{i, j \in {v_{xy}}} {\left( {{O_{ij}} + {I_{ij}}} \right)}, $ |
其中:vxy表示节点x到y之间建立最短通路可能经过的节点的集合,包含节点x和y;Oij、Iij分别表示i到j的出度值和入度值。IOxy表示节点x到y所有最短通路经过的节点的出度和入度总和,计算公式为
| $ I{O_{xy}} = \sum\limits_{i \in {v_{xy}}} {\left( {{O_i} + {I_i}} \right)} , $ |
其中:Oi表示节点i的出度;Ii表示节点i的入度。
1.2 转发行为用户之间的关注关系相对随意,无须身份验证即可关注,并且还存在友好性关注,实际可能并无共同兴趣爱好,也无相似的观点趋向,所以,用户之间的关注关系并不能完全代表两者之间关系的紧密度,只能作为度量用户之间的关系紧密度的一个因素,但不能完全依赖于关注关系这一种度量标准。微博内容能客观反映出用户的兴趣偏好,并且也可以合理地认为发布相同或相似内容的用户之间具有相同的兴趣爱好,但是兴趣爱好相同或相似并不等于关系紧密,因为两个完全无关的用户也可能发布相同的内容。所以本文考虑使用用户转发行为作为衡量关系密切程度的标准,如果两个用户互相转发对方微博的数量或者共同转发第三个用户微博的数量较多、两者微博被第三个用户转发的比例很大,可以认为两者更可能属于同一个社区。
用户x转发用户k的微博可以用一个向量Pk→x=(pk1→x, pk2→x,…,pkn→x)表示,pkn→x表示用户x转发用户k第n个微博的情况,pkn→x=1表示转发,pkn→x=0表示未转发。为方便计算,用户x自己发布的微博可以视为自己转发自己微博,即Px→x=(1, 1, …,1)。用户x和y对用户k的微博转发相似度计算公式为
| $ sim\left( {{\mathit{\boldsymbol{P}}_{k \to x, y}}} \right) = \left\{ {\begin{array}{*{20}{l}} {0, }&x 或 y 无任何转发, \\ {\frac{{{\mathit{\boldsymbol{P}}_{k \to x}} \times \mathit{\boldsymbol{P}}_{k \to y}^{\rm{T}}}}{{\left\| {{\mathit{\boldsymbol{P}}_{k \to x}}} \right\| \cdot \left\| {{\mathit{\boldsymbol{P}}_{k \to y}}} \right\|}}, }&其他, \end{array}} \right. $ |
其中:‖Pk→x‖、‖Pk→y‖分别表示Pk→x和Pk→y的欧几里得范数,Pk→x×Pk→yT是两者的点积。
用户x和用户y发表的微博被第三个用户j转发的相似度计算公式为sim(Px, y→j)=(nx→j×ny→j)/(Nx×Ny),其中:Nx、Ny分别表示用户x和用户y发表的微博总数;nx→k、ny→k分别表示用户x和用户y发表的微博被用户j转发的数量。
综上,用户x与用户y在整个社交网络结构中的转发行为相似度计算公式为
| $ si{m_{xy}} = \sum\limits_{k \in V} {sim} \left( {{\mathit{\boldsymbol{P}}_{k \to x, y}}} \right) + \sum\limits_{j \in V, j \ne x, y} {sim} \left( {{\mathit{\boldsymbol{P}}_{x, y \to j}}} \right)。$ |
用户x和用户y之间的联系紧密度包括两部分:1) 用户x和用户y之间的链路紧密度linkxy;2) 用户x和用户y转发行为相似度simxy。
用户x和用户y之间的紧密度计算公式为Closenessxy=αlinkxy+βsimxy,其中:α和β(α+β=1)分别表示链路紧密度和转发行为相似度的权重,即对用户间关系的贡献度。
1.3 社区中心的选择社交网络社区中心也称为种子节点,是一个社区内具有“影响力”的节点,这类节点一般具有两个特点:一是与社区内其他节点紧密度较大;二是与其他社区中心节点之间的紧密度较小,所以社区中心的选择对于社区划分的结果非常重要。社区中心的选择有社区中心数量和社区中心节点两个问题。
1) 社区中心数量代表最终社区的数量,但是实际上在社区划分之前,一般不能确定社交网络当中存在多少社区结构。在传统的网络社区挖掘中,K-MEANS等经典的聚类方法取得了很好的划分效果,但是,这类聚类方法共同的缺点就是需要指定社区数量,这在实际应用中难以做到。Louvain算法[15]是大型网络社区结构挖掘算法,它根据模块度增量确定合并的节点,自底向上进行合并,直到整个网络的模块度不再变化或者变化极小。因为合并后节点急剧减少,所以能够处理大规模网络结构,并且时间开销较少,效率高。本文使用该算法来确定社区数量,因为只是确定大致社区数量,对社区质量要求不高,所以此处利用链接紧密度作为度量即可。算法执行停止后产生的社区数量即为该社交网络内包含的社区结构数量。
2) 社区中心节点是社区的核心,确定社区数量之后,就要选出相应数量的中心节点,本文算法选择社区中心节点的方法为:将所有节点形成一个集合,计算所有节点的出度和入度之和,并降序排列,因为社区中心局部内聚性强,所以社区中心的出度和入度之和相对较高;然后取出度与入度之和最高的节点作为其中一个中心节点,并计算该节点与其他每个节点的链接紧密度,根据链接紧密度计算公式,链接紧密度小于0.5的节点肯定不相邻,而中心节点之间也不可能相邻,所以选出链接紧密度小于0.5的节点形成新的集合,重复以上步骤,直到取出的中心节点数与目标社区数量相等为止。中心节点选择算法流程如下。
输入:社交网络节点集合Set,社区数量M。
输出:中心节点集合Center。
S1) for Set集合中的每个节点I;
S2) 计算IOi=Ii+Oi,存储于集合IO中;
S3) 将IO中的元素按节点度降序排序;
S4) if IOk最大,将节点k移入Center集合,标记IOk;
S5) for Set集合中的每个节点j,j≠k;
S6) iflinkjk≥0.5;
S7) 标记IOj;
S8) if集合IO剩余节点数小于M减去集合Center节点数;
S9) 撤销所有已选中心节点,标记其中出入度最大的节点,重复S4~S9直到Center集合中元素数等于M;
S10) 返回中心节点集合Center。
在实验中,对实验数据进行了清洗,将出度和入度比例比较极端的节点去除,剩余节点中,出度或入度偏大的节点,可能正是要选取的中心节点,或是社区重叠的部分,并且,在选择中心节点过程中,如果出现剩余节点数量较少,以至于最终不足M个社区中心节点的情况,则说明在已选的中心节点中,存在几乎与其他所有节点均存在直接关注关系的节点,那么该节点只有两种情况:一是出度和入度比较极端的节点;二是高度重叠的节点。如果是前者,在数据清洗阶段已经处理。如果是后者,该节点的出入度则异常大,将直接排除,不再作为备选中心节点。中心节点选择的原则就是找出M个出入度较大但又相互联系松散的节点。
1.4 节点所属社区分配假设网络中存在M个社区,节点vi对各社区的归属度记为φi=(φi, 1,φi, 2,…,φi, m),其中φi, m表示节点vi对社区m的归属度。一般情况下,可以合理地认为社区中心不会同时属于多个社区,所以社区中心节点ci只归属于节点ci所代表的社区,对其他社区的归属度为0,这就能保证初始状态下每个社区都有一个节点。非中心节点对各社区的归属度用该节点与社区现有节点紧密度的平均值来计算, 并将节点归属到获得最高平均值的社区。非中心节点vi对社区m的归属度计算公式为
另外,对于重叠社区,主要是发现节点是否同时归属多个社区。本文中,如果节点对多个社区的归属度满足一定的条件,则认为同属于多个社区。假设社区p中的节点vi对社区q的归属度满足φi, q/φi, p>θ(0 < θ < 1), 则将vi作为社区p和q的重叠节点,并同时归属到社区p和q中。节点所属社区的分配过程即本文提出的基于链路结构和转发行为的微博社交网络重叠社区划分方法(algorithm based on link structure and forwarding behavior,ABLF)如下。
输入:中心节点集合Center,网络节点集合V。
输出:社区结构。
S1) 确定社区数量M;
S2) 执行中心节点选择算法,选取M个社区中心点;
S3) for集合Center中每个节点ci;
S4) for m=1, 2, …,M个社区;
S5) if ci是第m个社区的中心;
S6) φci, m=1;
S7) ELSE;
S8) φci, m=0;
S9) for V-Center中的每个节点vi;
S10) for m=1, 2, …,M个社区;
S11) 计算φi, m;
S12) 将节点vi归属到φi, m最大的第m个社区;
S13) if φi, q/φi, m>θ;
S14) 将节点vi作为第m个社区和第q个社区的重叠节点,并归属到第q个社区;
S15) 返回M个社区结构。
2 实验及结果分析 2.1 实验数据本文所用实验数据为新浪微博数据,使用网络爬虫程序,从某一种子节点开始,爬取该用户一年内的微博数据,包括该用户所发微博内容,以及从他人微博转发的内容,并将爬取内容以单文件形式保存下来,然后根据深度优先原则遍历该用户的粉丝账号和其关注的账号,将遍历到的账号以队列形式保存,队列中的每个账号都逐个做上述处理。经过一段时间的爬取,实验室从新浪微博获取近1 000万个用户账号、关注关系、微博内容。为了实验应用,实验室成员从中抽取出三类实验数据:第1类实验数据是从爬取的全部数据中抽取出5个训练数据集,无标记,节点数分别为97个、121个、105个、154个、139个,数据内部连边数分别为1 113条、1 407条、1 265条、1 842条、1 611条,用于测试θ取值较优点;第2类数据是经过人工标记的NBA篮球、足球联赛和韩剧相关的微博信息,这些数据组成的社交网络子网络中共有133个节点、1 531条边,存在重叠节点;第3类数据是从爬取的所有数据中抽取8 745个节点和637 051条边组成的微博社交网络。三类数据均为清洗后的数据,已将入度过大但出度较小、入度过小但出度较大或出、入度中一方为零的节点删除。实验前,对于前两类数据,节点较少,将出、入度或入、出度比例大于100∶1的节点去除,对于第三类数据,将比例大于1 000∶1的节点去除。本文将在这三类数据集上用ABLF算法进行实验并分析实验结果。
2.2 评价标准已经过人工标记的实验数据可以采用准确率、召回率和F1值来衡量社区划分的结果。为了适应对社区划分结果的评价,本文对上述三种度量适当调整,采用平均准确率(AVG_P)、平均召回率(AVG_R)和平均F1值(AVG_F1)进行度量。
1) 平均准确率为在本次社区划分结果中,被正确划归到所属社区的节点数占社区内节点总数的比例的平均值。
2) 平均召回率为在本次社区划分结果中,被正确划归到所属社区的节点数占社区实际节点总数的比例的平均值。
3) 平均F1值是综合评价准确率与召回率的指标。
未经人工标记的实验数据,是最真实的社交网络数据,社区结构暂不明确,这将更能真实反映算法对实际社交网络的适应性,但是也正因为社交网络用户所属社区事先不知,所以社区划分的结果也没有对比的对象,就没有精确的衡量标准来评价社区划分的质量。在社区挖掘领域,常用Newman等[14]提出的模块度来衡量社区质量,模块度Q使用社区内边的比例与其期望值的比计算,但是本文算法除了依赖于社交网络中的边,还依赖于用户转发行为,所以原模块度计算方法将稍作修改,以便更好地适应本文算法。新的模块度计算方法为
使用获取的三类实验数据分别设计实验,将本文ABLF算法、SL3PA算法[2]、CDCLM算法[3]、COPRA算法[9]和IEDC算法[10]进行对比实验。因为在实际社区划分时,链路结构和转发行为同等重要,所以α和β均设置为0.5,查看θ取不同值时的社区划分结果变化情况。
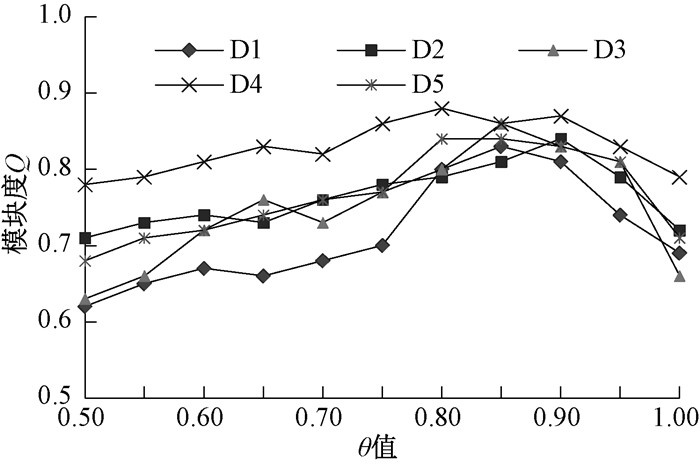
1) θ取值直接影响重叠社区划分的结果,θ取值太小,会导致社区重叠度较高,甚至完全重叠,如果θ取值太大,又会出现社区重叠太小,甚至无任何重叠。为了分析参数θ对重叠社区划分的影响,取值在0.5~1之间逐渐增加,每次增加0.05,在第1类五个训练数据上执行ABLF算法,查看在θ不同取值下,社区划分结果的模块度变化情况,实验结果如图 1所示。在五个训练数据上运行ABLF算法,在D1和D3上,当θ为0.85时模块度达到峰值,然后回落;在D2和D4上当θ分别为0.9或0.8时模块度达到峰值,然后回落;在D5上当θ为0.8时模块度达到峰值,并且θ为0.85时尚未回落。从实验可知,θ取值在区间[0.8, 0.9]为宜,所以在后面的实验中,本文ABLF算法的θ值均取0.85。
|
图 1 参数θ对模块度的影响 Fig. 1 Parameter θ Impact on modularity |
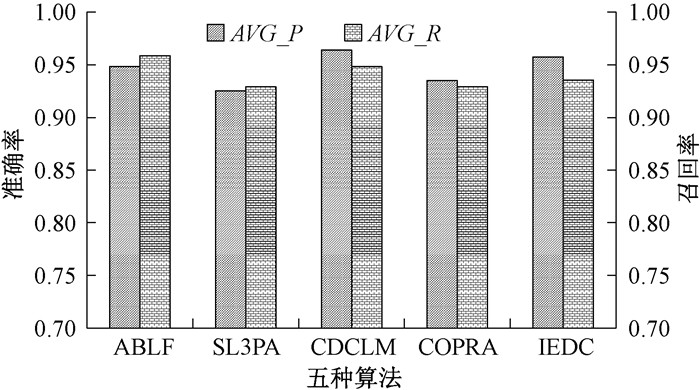
2) 将本文算法与其他四种算法应用于经人工标记的实验数据。实验结果显示,五种方法都成功将该社交网络子网络划分为三个社区,由于该数据已经进行人工标记,也就是社区所包含的节点已经确定,收集实验返回数据,分别计算五种算法得出的结果的平均准确率、平均召回率和平均F1值。五种算法得出的社区划分结果的平均准确率和平均召回率对比如图 2所示。
|
图 2 平均准确率和平均召回率对比 Fig. 2 Comparison of average accuracy and average recall rate |
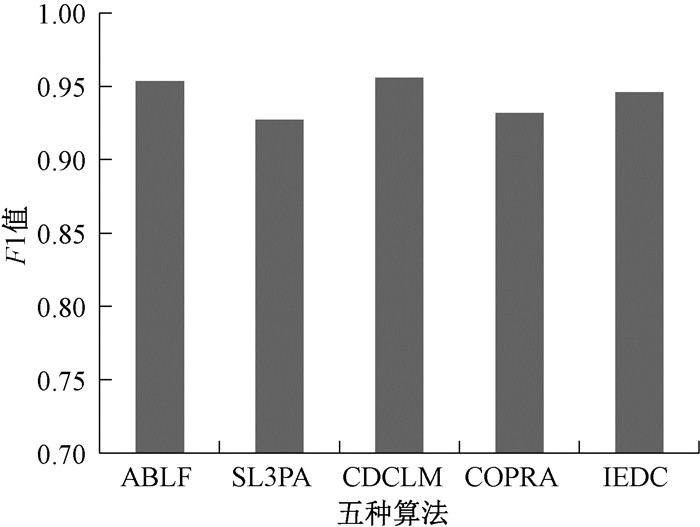
从图 2可以看出,ABLF算法的平均正确率和平均召回率都比较高,两个指标都高于SL3PA算法和COPRA算法,与CDCLM算法和IEDC算法相比,平均准确率略低但平均召回率略高于这两种算法。准确率和召回率在某种意义上可以作为社区划分质量的评估标准,准确率和召回率越高越好,但是,两者之间也存在一定的矛盾性。假如在某种极端情况下,某社区所有节点都归属到该社区,但同时也有大量非本社区节点归属进来,那么该社区召回率就是100%,但是准确率却很低,同理,准确率高,召回率也可能很低。F1度量综合考虑这两种衡量标准,两者都高,则F1也高,其中一个值低,则F1也低,能有效避免准确率和召回率极端不平衡的情况,五种算法社区挖掘结果的平均F1值如图 3所示。从F1度量值来看,ABLF算法社区划分结果的平均F1值明显高于SL3PA算法和COPRA算法,略高于IEDC算法,略低于CDCLM算法,相差不大。
|
图 3 F1-measure对比 Fig. 3 Comparison of F1-measure |
在已标记的数据集上的实验显示,本文提出的ABLF算法所挖掘的社区质量相对较高。经分析,这种结果的产生原因在于ABLF算法衡量微博用户之间紧密度不仅仅依赖于网络结构,也就是不仅仅考虑用户之间的关注关系,还综合衡量了用户之间的转发行为。实际上,用户之间的关注不能客观反映其联系紧密度或者兴趣相似度,因为可能存在以关注获得利益的“水粉”,而用户之间对第三者微博的转发行为或者第三者对他们的转发行为更能反映用户的紧密程度。比如某用户关注了大量篮球爱好者,但是该用户所发表或者转发的微博多是韩剧相关内容,那么该用户属于韩剧相关社区更为合适,它对篮球爱好者的关注或许只是源于友情而非爱好,而其他方法多是忽略了用户之间的这种行为相似度,导致社区划分质量略低。
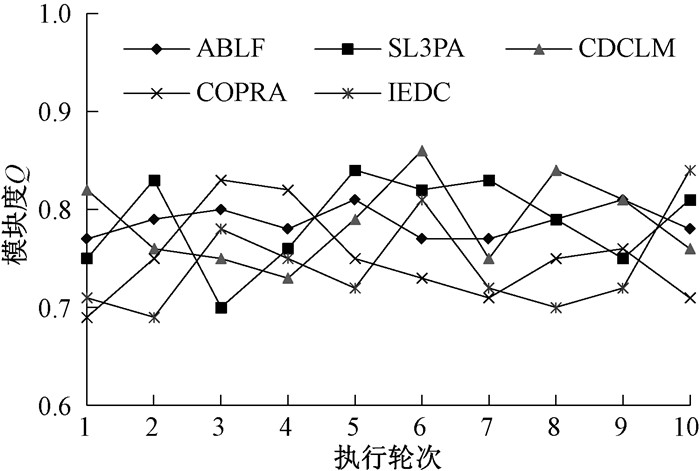
3) 第三类数据更贴近实际社交网络数据,未经严格的数据清洗和标记,数据内社区结构不明朗,所以不能再用正确率和召回率来衡量结果,在本实验中使用模块度度量。将本文算法和其他四种算法均重复执行10次,不但能衡量社区划分的结果质量,也能突显算法的稳定性,只有社区划分质量好并且结果相对稳定的算法才是好的。五种算法重复执行10次产生的社区划分结果的模块度如图 4所示。
|
图 4 社区划分结果对比 Fig. 4 Comparison of community partition results |
从图 4可以看出,五种算法重复执行的情况下,本文ABLF算法社区划分结果的总体的模块度平均值略优于COPRA算法和IEDC算法,比SL3PA算法稍低,与CDCLM算法持平,但是本文ABLF算法重复执行的情况下表现比较稳定,划分结果的质量波动平缓,每次执行结果差别不大,但是其他四种算法都表现出较大的波动性,原因在于社区划分的结果一定程度上取决于社区中心的选择,本文ABLF算法的社区中心节点选择方法比较客观,多次重新选择社区中心的情况下,被选中的中心节点不会有较大变动,即使某社区在上一轮执行时被选中的社区中心节点为A,而本轮选中了节点B,根据本文社区中心选择算法可知,A与B的出度与入度之和可能相当,只是在社区中所处位置不同,虽然会影响社区划分结果,但影响不大。其他几种算法也表现出了很好的划分效果,甚至平均来看更优于本文ABLF算法,但是可能未完全考虑网络链路和用户行为相似性,导致划分结果受个别特殊用户的影响,稳定性稍差。另外,因为此数据为未标记数据,未严格清洗,存在部分相对孤立的节点,所以整体的模块度远低于人工标记的经严格清洗的数据。
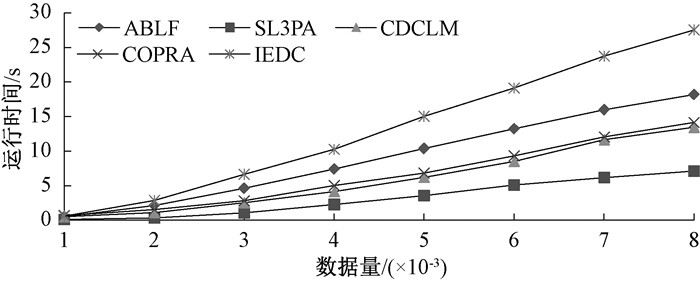
4) 为验证算法时间开销,从第三类数据中抽取不同数量的节点来测试在不同规模数据上的运行时间。SL3PA标签传播算法相当于节点的遍历操作,时间开销较小;CDCLM算法使用局部模块度的计算来降低时间开销,效果比较明显,并且在数据量逐渐增加的情况下,时间开销未出现陡增的现象;COPRA算法利用数据降维技术,减小数据维度,节省运行时间;IEDC算法在发现社区结构过程中,对特征矩阵的循环处理和更新增加了时间开销。不同规模数据上的运行时间如图 5所示。
|
图 5 算法运行时间 Fig. 5 Running time of algorithms |
从图 5可以看出,ABLF算法在时间开销上相较于SL3PA算法、CDCLM算法和COPRA算法来说有些偏高,比IEDC算法低,原因在于ABLF算法在中心节点选取以及节点所属社区分配过程中,需要计算多节点对之间的联系紧密度,增加了时间开销。
3 总结本文提出一种基于链路结构和转发行为的微博社交网络重叠社区划分方法,在对社交网络链路结构进行分析的同时,综合考虑了用户转发行为的相似性,将两者结合,进一步提高了社区划分结果的质量。实验证明了本文ABLF算法不但取得了较好的重叠社区划分效果,还具有更好的稳定性。但是,本文算法还存在几点不足,比如,时间开销略高,对θ取值未进行严格的学习训练。下一步工作的重点是深入分析用户转发行为,设计转发行为预测模型,为用户转发行为预测分析提供依据。
| [1] |
CHOUCHANI N, ABED M. Online social network analysis: detection of communities of interest[J]. Journal of intelligent information systems, 2020, 54(2): 5-21. (  0) 0) |
| [2] |
MAHABADI A, HOSSEINI M. SLPA-based parallel overlapping community detection approach in large complex social networks[J]. Multimedia tools and applications, 2021, 80(5): 6567-6598. DOI:10.1007/s11042-020-09993-1 (  0) 0) |
| [3] |
LIU Z H, XIANG B J, GUO W Z, et al. Overlapping community detection algorithm based on coarsening and local overlapping modularity[J]. IEEE access, 2019, 7: 57943-57955. DOI:10.1109/ACCESS.2019.2912182 (  0) 0) |
| [4] |
KUMAR A, BARMAN D, SARKAR R, et al. Overlapping community detection using multiobjective genetic algorithm[J]. IEEE transactions on computational social systems, 2020, 7(3): 802-817. DOI:10.1109/TCSS.2020.2989295 (  0) 0) |
| [5] |
MESSAOUDI I, KAMEL N. Overlapping community detection with a novel hybrid metaheuristic optimisation algorithm[J]. International journal of data mining, modelling and management, 2020, 12(1): 118-139. DOI:10.1504/IJDMMM.2020.105601 (  0) 0) |
| [6] |
TRIVEDI K, RAMANNA S. Overlapping community detection in social networks with Voronoi and tolerance neighborhood-based method[J]. Granular computing, 2021, 6(1): 95-106. DOI:10.1007/s41066-019-00207-0 (  0) 0) |
| [7] |
李政廉, 吉立新, 黄瑞阳, 等. 面向大规模网络的快速重叠社团挖掘算法[J]. 电子学报, 2019, 47(2): 257-265. LI Z L, JI L X, HUANG R Y, et al. Fast overlapping communities detection algorithms for large-scale social networks[J]. Acta electronica sinica, 2019, 47(2): 257-265. DOI:10.3969/j.issn.0372-2112.2019.02.001 (  0) 0) |
| [8] |
KUMAR P, DOHARE R. A neighborhood proximity based algorithm for overlapping community structure detection in weighted networks[J]. Frontiers of computer science, 2019, 13(6): 1353-1355. DOI:10.1007/s11704-019-8098-0 (  0) 0) |
| [9] |
JAVED M A, YOUNIS M S, LATIF S, et al. Community detection in networks: A multidisciplinary review[J]. Journal of network and computer applications, 2018, 108(4): 87-111. (  0) 0) |
| [10] |
HAJIABADI M, ZARE H, BOBARSHAD H. IEDC: An integrated approach for overlapping and non-overlapping community detection[J]. Knowledge-based systems, 2017, 123(5): 188-199. (  0) 0) |
| [11] |
杜航原, 王文剑, 白亮. 基于网络节点中心性度量的重叠社区发现算法[J]. 计算机研究与发展, 2018, 55(8): 1619-1630. DU H Y, WANG W J, BAI L. An overlapping community detection algorithm based on centrality measurement of network node[J]. Journal of computer research and development, 2018, 55(8): 1619-1630. (  0) 0) |
| [12] |
闫涵, 康海燕. 有向重叠社区下考虑兴趣度的谣言免疫策略研究[J]. 郑州大学学报(理学版), 2020, 52(4): 82-88, 95. YAN H, KANG H Y. Rumor immunization strategy with community interest degree in directed overlapping community[J]. Journal of Zhengzhou university (natural science edition), 2020, 52(4): 82-88, 95. (  0) 0) |
| [13] |
陈珂, 梁斌, 左敬龙, 等. 一种用于中文微博情感分析的多粒度门控卷积神经网络[J]. 郑州大学学报(理学版), 2020, 52(3): 21-26, 33. CHEN K, LIANG B, ZUO J L, et al. Multiple grains-gated convolutional neural networks for Chinese microblog sentiment analysis[J]. Journal of Zhengzhou university (natural science edition), 2020, 52(3): 21-26, 33. (  0) 0) |
| [14] |
NEWMAN M E J. Communities, modules and large-scale structure in networks[J]. Nature physics, 2012, 8(1): 25-31. DOI:10.1038/nphys2162 (  0) 0) |
| [15] |
BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks[J]. Journal of statistical mechanics: theory and experiment, 2008, 2008(10): 10008. DOI:10.1088/1742-5468/2008/10/P10008 (  0) 0) |
 2021, Vol. 53
2021, Vol. 53

