2. 福建省农田建设与土壤肥料技术推广总站,福州 350003;
3. 仙游县土壤肥料技术推广站,福建仙游 351200
2. Fujian Cropland Construction and Soil and Fertilizer Station, Fuzhou 350003, China;
3. Soil and Fertilizer Technology Extension Station, Xianyou County, Xianyou, Fujian 351200, China
近 10 年来,我国各地在测土配方施肥工作中完成了众多的作物氮磷钾肥效试验。然而这些多点分散试验资料必须合理分类总结,才能为制定推荐施肥方案提供科学依据。迄今不少学者研究提出了许多肥料试验资料的分类或聚类方法,诸如在早期提出的经验聚类法、连续函数法、t 检验聚类法、协方差聚类法等[1]。在 20 世纪 80 年代前后,Colwell 等[2]提出了回归系数平均法,王兴仁等[3]提出分类回归综合法,毛达如等[1]提出动态聚类法,杨寿春等[4]提出按照无肥区产量水平划分归类等,吴良欢等[5]对水稻肥料效应的分类方法及其类内距离阈值的确定方法进行了探讨。王兴仁等[3]详细阐述了多点肥效试验资料进行分类汇总的理论基础,毛达如等[1]提出了类特征肥效方程的概念,即根据在同一个土壤肥力等级或同一个施肥类别内的多点试验资料,取各试验处理产量平均值所建立的肥料效应方程。纵观现有肥料效应分类或聚类方法,都是从多点肥料试验结果中找出具有一定代表性的类肥料效应方程作为推荐施肥的依据。但是,有关不同聚类分析方法的有效性以及分类结果在类与类之间是否具有统计显著性差异,在以往的研究中未引起足够的重视。近年来,虽然系统聚类方法在土壤学中得到广泛的应用[6–10],但却鲜见在肥料效应方程领域的相关研究报道。
为此,本研究根据福建省仙游县早稻的多点氮磷钾肥效试验资料,探讨不同系统聚类方法对定量分类效果的影响,并进行类别间差异显著性检验,旨在为多点田间试验资料的归纳汇总和施肥决策提供科学依据。
1 材料与方法 1.1 试验设计以仙游县 2007 年至 2009 年的早稻试验资料为例。这些试验均采用“3414”设计方案,共 14 个处理,即:1) N0P0K0;2) N0P2K2;3) N1P2K2;4) N2P0K2;5) N2P1K2;6) N2P2K2;7) N2P3K2;8) N2P2K0;9) N2P2K1;10) N2P2K3;11) N3P2K2;12) N1P1K2;13) N1P2K1;14) N2P1K1。其中,“2”水平的当地推荐施肥量为 N 165 kg/hm2、P2O550 kg/hm2 和 K2O116 kg/hm2,“0”水平表示不施肥,“1”水平的用量为“2”水平的 50%,“3”水平的用量为“2”水平的 150%。选择当地具有代表性的土壤类型和肥力水平的稻田作为试验地。
试验采用多点分散不设重复和区组排列的试验方法,小区面积 20 m2。供试品种选用当地大面积种植的良种。氮肥用尿素 (N 46%),磷肥用过磷酸钙 (P2O512%),钾肥则用氯化钾 (K2O 60%)。基肥中的氮、钾肥占总用量的 50%,磷肥做基肥施用,余下的氮、钾肥在水稻分蘖期施用。试验区周围设 1 m 宽以上的保护行,其它的栽培管理措施与大田生产一致。试验水稻收获时,各小区单收单称,分别记录鲜重产量和晒干重,各试验点的供试土壤类型和主要处理产量结果见表 1。
| 表1 早稻各试验点供试土壤类型和主要处理产量 Table 1 Soil types and the early rice yields in the main treatments of the experiment sites |
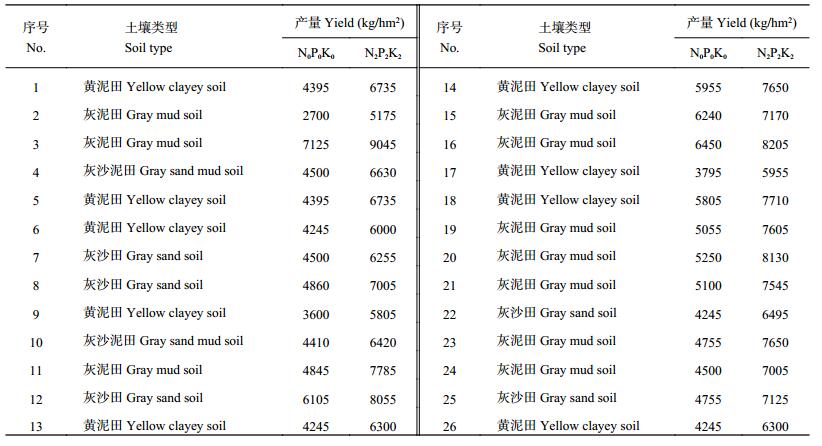 |
每个田间试验实施前,按规范采集一个混合基础土样。用常规方法[11]测定土壤主要理化性状,其中,pH 为电位法,有机质为重铬酸钾容量法,碱解氮为碱解扩散法,Olsen-P 为 0.5 mol/L 碳酸氢钠提取—钼锑抗比色,速效钾为 1 mol/L 乙酸铵提取—火焰光度计测定。26 个供试土壤的 pH 为 5.4 ± 0.2,土壤有机质为 22.8 ± 5.1,土壤碱解氮、Olsen-P 和速效钾含量分别为 143.1 ± 45.9、28.8 ± 23.8 和 37.8 ± 24.8 mg/kg。
1.2 系统聚类分析方法目前,系统聚类分析的数学方法有很多种[12],本文选用在土壤学中有代表性的几种聚类方法[13]。其中,描述样本间“距离”的数学表达式分别选用欧氏距离、街区距离和相似系数等 3 种方法。
欧氏距离的计算公式为:
| $d_{il} = \sqrt {\sum\limits_{j = 1}^m {{{(x_{ij} - x_{lj})}^2}} } $ | (1) |
街区距离的计算公式为:
| $d_{il} = \sum\limits_{j = 1}^m {\left| {x_{ij} - x_{lj}} \right|} $ | (2) |
相似系数的计算公式为:
| $d_{kj} = \frac{{\sum\limits_{i = 1}^n {(x_{ik} - \bar x_{k})(x_{ij} - \bar x_{j})} }}{{\sqrt {\sum\limits_{i = 1}^n {{{(x_{ik} - \bar x_{k})}^2} \cdot \sum\limits_{i = 1}^n {{{(x_{ij} - \bar x_{j})}^2}} } } }}$ | (3) |
式 (1)、(2) 和 (3) 中,i 和l 是试验点编号,i,l 等于 1、2、3、…、n,n 为试验点总个数。k 和j 为各试验点处理编号,k 和j 等于 1、2、3、…、m,m 为各试验点处理数,m = 14。例如,xij 和xlj 分别表示第i、l 试验点的第j 处理产量。
聚类方法分别选用最短距离法、最长距离法和离差平方和法等 3 种方法。其中,离差平方和法的计算公式为:
| $S_{t} = \sum\limits_{i = 1}^{nt} {\sum\limits_{j = 1}^m {{{(x_{{tij}} - \bar x_{tj})}^2}} } $ | (4) |
式中,t 表示类别Gt
,nt
表示类别Gt
的试验点数,其它符号的意义与上述公式相同。xtij
表示类别Gt
中第i 个试验点的第j 处理产量,
在聚类分析中,类别之间差异显著性检验常用F 检验,用于判断两两类别间的差异是否显著。F 值计算公式[14]为:
| $F = \frac{{(n{\rm_{1}} + n_{2} - 2) - m + 1}}{{(n_{1} + n_{2} - 2)m}}{T^2}$ | (5) |
其中,
具体聚类分析过程和聚类谱系图绘制采用 MATLAB R2014a 软件的统计分析工具箱完成。
2 结果与分析 2.1 不同聚类方法对分类结果的影响图 1和图 2的聚类分析结果表明,不同聚类方法对 26 个早稻“3414”氮磷钾肥效试验的 14 个处理产量的分类效果有很大的差异。当采用欧氏距离时,最短距离法 (图 1a) 的纵坐标并类距离空间最大只有 250 左右,聚类谱系图甚至出现单方向的“楼梯”状,以致无论采用何种不同的阈值,除其中的一个类别外,其余类别都只含 1 个或者少数几个样本,分类效果最差;最长距离法 (图 1b) 的纵坐标并类距离空间扩张到 1000 左右,分类效果有明显改善,但是,分成 3~5 类时,3 号试验点被单独分成一类,导致该类别因试验点数太少而缺乏代表性;离差平方和法 (图 1c) 的纵坐标并类距离空间进一步扩张到 1500 左右,可将 26 个试验点清晰地分成 3 类,而且每一类都包含若干个试验点,具有最佳的聚类效果。采用街区距离法的分类效果与欧氏距离法大致相同。
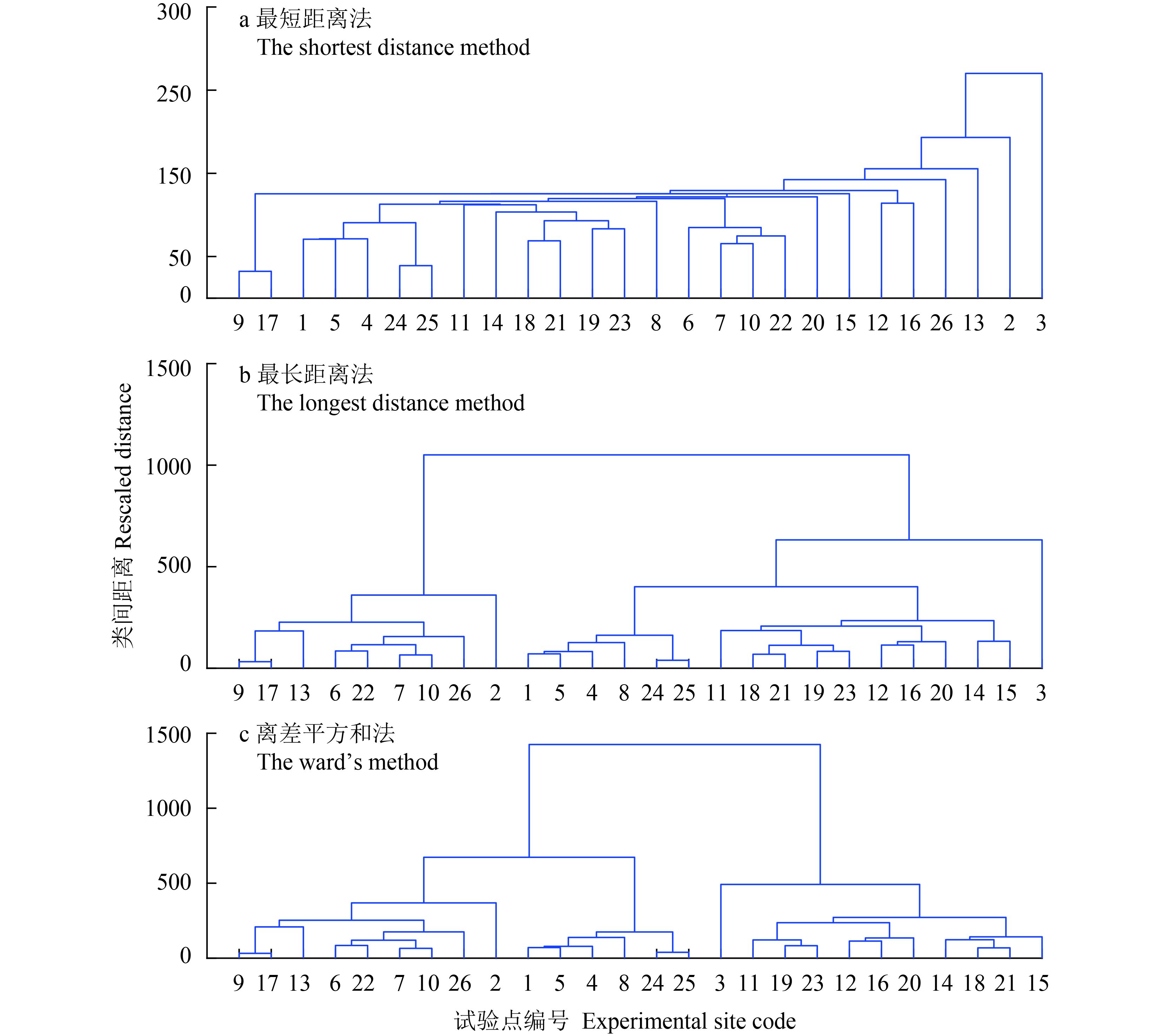 |
| 图1 欧氏距离的聚类结果 Fig. 1 Clustering results of the Euclidean distance |
采用相似系数作为样本间距离的表征时,最短距离法、最长距离法和离差平方和法,也会使样本并类距离空间呈现扩展的趋势,但都被限制在小于或等于 1,导致图 2a和图 2b的聚类谱系图都出现“楼梯”状,不能将 26 个试验点清晰分类,但图 2c的离差平方和法聚类效果在聚类谱系图上与图 1c相似。
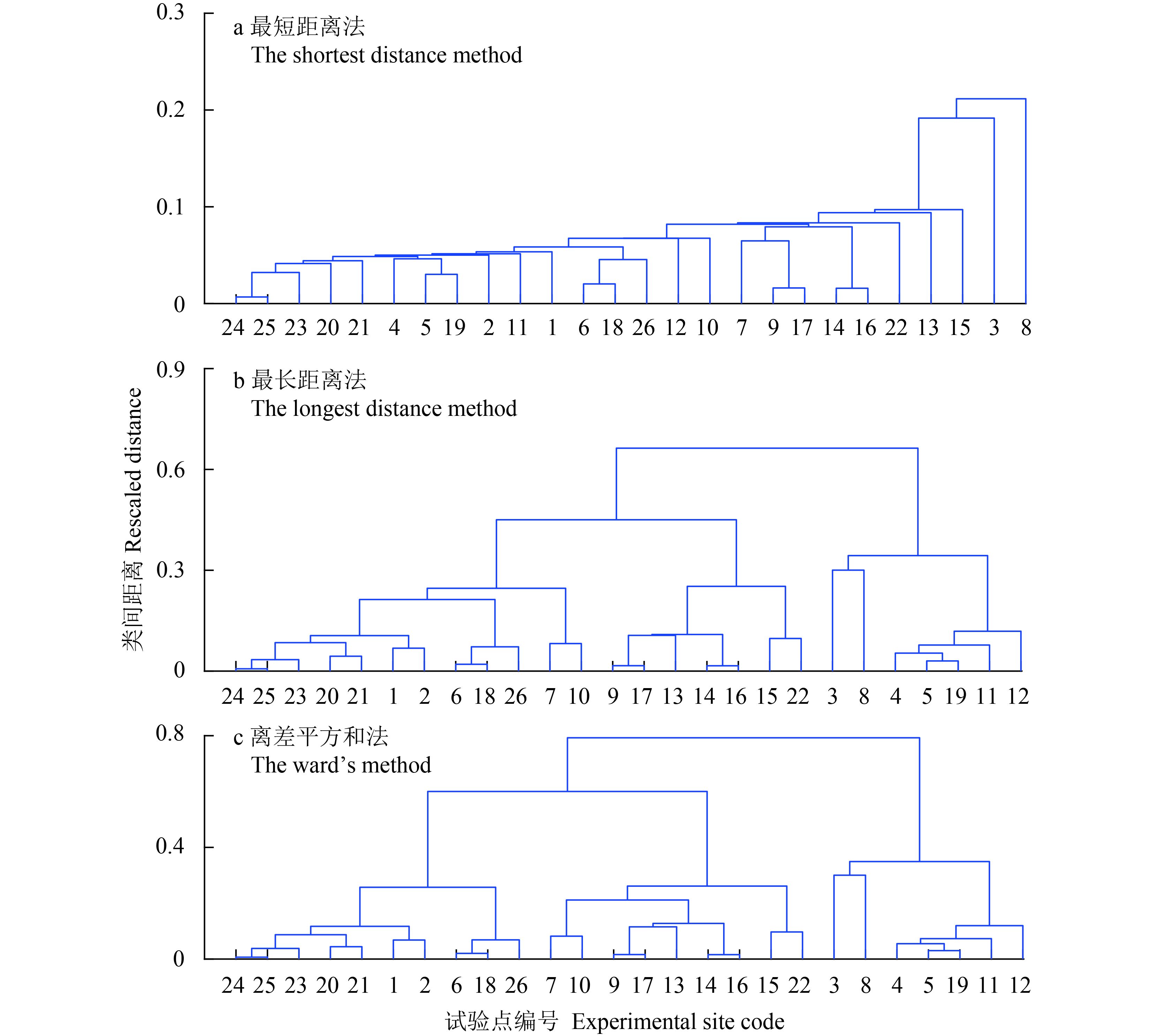 |
| 图2 相似系数法聚类结果 Fig. 2 Clustering results of the similarity coefficient method |
因此,从聚类谱系图看,对仙游县 26 个早稻氮磷钾肥效试验结果而言,离差平方和法具有最好的分类效果。
2.2 肥效类别间差异显著性检验不同聚类分析方法得到的各类别所含试验点序号结果见表 3。从图 1c和图 2c的聚类图可以清楚看到,对 26 个试验点的最佳分类数应为 3 类,但是,分成 3 类是否真的合理?还需要进行统计检验。
| 表2 不同聚类分析结果的试验点归属和类间均值差异显著性检验 Table 2 Sample belongings of the clustering analysis and the mean value difference significance test between the classes |
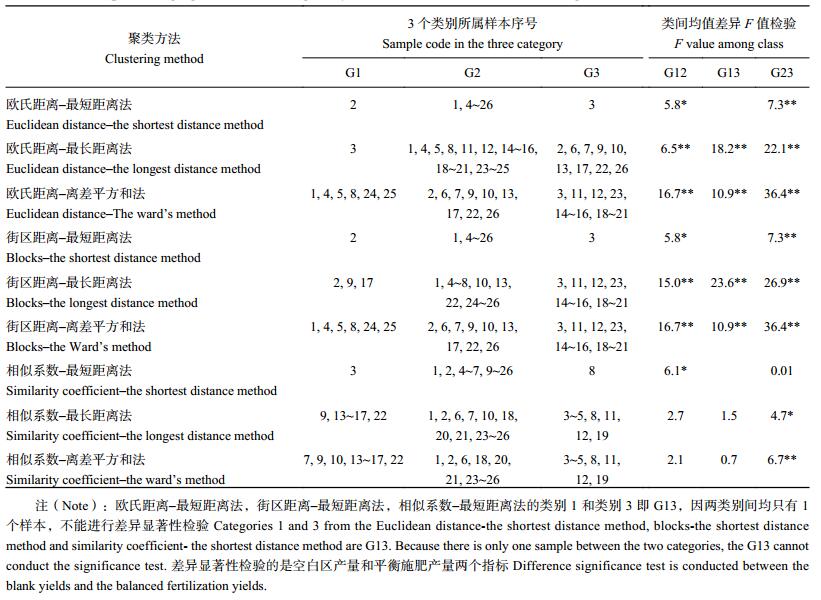 |
在数理统计中,为了使有关统计量能够准确计算或得到有意义的结果,都要求样本数必需大于观测指标数。针对“3414”设计的肥效试验,每个试验点有 14 个处理,即每个样本有 14 个产量指标。因此,要进行类别间 14 个产量均值的差异显著性检验,每个类别必需要有 14 个以上试验点。表 2结果显示,多数施肥类别均达不到此要求,因而不可能将每个试验的 14 个处理都用来作为检验的产量观测指标。事实上,在施肥实践中,空白产量和平衡施肥产量才是最重要的施肥参考指标,故只需确保这 2 个产量指标在类别间有显著差异,即可满足指导施肥的需要。参考傅德印方法[16],将各试验点的处理 1 空白区产量和处理 6 平衡施肥产量这两个指标,作为类别间差异显著性检验的依据,结果见表 3。
F 检验结果表明,用相似系数表征各试验点间“距离”的聚类分析效果最差,欧氏距离和街区距离的聚类效果大体相当,与图 1和图 2的聚类谱系图结果相一致。具体而言,欧氏距离和街区距离对应的最长距离法和离差平方和法组成的 4 种聚类方法具有较好的效果。在 3 个类别中,两两类别均值差异均达到极显著水平,表明它们的分类结果都是有效的。但是,欧氏距离—最长距离法的类别 1 只含有一个试验点,缺少代表性;与街区距离相比,欧氏距离具有明确的几何意义。因此,针对仙游县的县域 26 个试验资料而言,欧氏距离–离差平方和法是最佳系统聚类分析方法。
2.3 早稻氮磷钾肥效的类特征肥效方程根据欧氏距离–离差平方和的系统聚类方法,对照 26 个试验点在 3 个类别中的归属 (表 2),结果表明,该聚类方法综合反映了县域稻田的肥力状况和生产力。其中,类别 1 (G1) 的 6 个试验点中,灰沙田土属占了 4 个,另外 2 个是黄泥田土属,表明是以灰沙田为主的类特征肥效函数类别;该类农田大都位于河流两岸或坡地与平地交界处,生产条件尚好,但漏水漏肥较严重,是当地的中产田;类别 2 (G2) 的 9 个试验点中,黄泥田土属占了 5 个,灰沙田和灰泥田土属各占 3 个和 1 个,是以黄泥田土属为主的类特征肥效函数组别;该类农田大都位于丘陵坡地上或远离村镇的耕地,土壤理化性状和生产条件普遍较差,是当地的低产田。类别 3 (G3) 的 11 个试验点中,灰泥田土属占了 8 个,黄泥田和灰沙田土属各占 2 个和 1 个,表明该组是以灰泥田土属为主的类特征肥效函数类别;该类土壤肥力较高,生产条件较好,是当地的高产田。
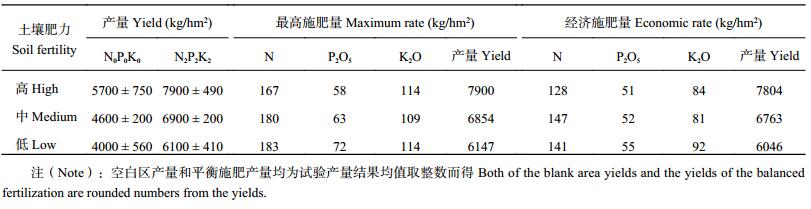
对处理 1 和处理 6 试验产量的统计结果 (表 3) 表明,由于县域内生产条件和生产水平差异较小,类内产量变异很小。在高、中、低三个肥力等级类别中,空白区产量的变异系数分别只有 13.3%、4.3% 和 14.1%,平衡施肥产量的变异系数则分别只有 6.2%、2.9% 和 6.7%。结果表明,在 95% 置信水平下,稻谷产量水平在 3 个类别间几乎不出现交叉重叠,结果提高了早稻不同施肥类别在推荐施肥量上的唯一性和可靠性。为求得各施肥类别的推荐施肥量,分别对各类别的相应试验结果计算各处理产量均值[1],建立三元二次多项式肥效模型 (表 3),表明 3 个类特征肥效方程均达到统计显著水平,典型性判别[15]表明它们均属于典型肥效函数。因此,根据表 3的类特征肥料效应方程以及当地肥料和稻谷市场平均价格,用边际产量导数法计算试验区域内的最大施肥量和经济施肥量及其预计产量 (表 4),结果为仙游县不同产量水平的早稻合理施肥提供了定量施肥依据。
| 表3 仙游县早稻氮磷钾类特征肥效方程和空白区、平衡施肥处理产量 Table 3 Response function of early rice to N, P and K fertilization and the yields in blank and balanced fertilization treatments in Xianyou County |
 |
| 表4 仙游县不同肥力等级或目标产量早稻推荐施肥量 Table 4 Fertilization recommendation for early rice in different soil fertility and target yields in Xianyou County |
 |
虽然数学家们对聚类分析方法做了许多研究和讨论[12],但是目前还没有一个公认和最佳的具体聚类方法。图 1和图 2可以看出,同样 26 个试验资料,用不同方法所得的聚类效果有很大的差别。凡是使纵坐标并类距离空间扩张范围较大的系统聚类分析方法都有较清晰的分类效果,而使纵坐标并类距离空间压缩的方法都会导致类别分辨力下降。
从数学上看,本研究选中的最短距离法、最长距离法和离差平方和法三种聚类方法,前者使样本或类的空间距离被压缩,后者使空间距离扩张,而离差平方和法则使样本或类的空间距离进一步扩张。刘多森等[13]研究表明,使距离空间浓缩的方法会导致分类灵敏度降低,使距离空间扩张的方法会提高分类灵敏度,但灵敏度过高有时可能出现不合理的结果。因此,若被研究的样本差异较大时,采用最短距离法可能会有较好的效果,反之分类效果就可能很差。本文研究的 26 个早稻氮磷钾试验资料都来自仙游县,区域范围较小,生产条件和生产水平差异不大,样点间的“距离”较小。因此,采用最短距离法的分类效果不佳 (图 1a和图 2a),而采用使样点或类的距离空间较大程度扩张的离差平方和法,提高了分类灵敏度,能将 26 个试验点清晰地分成3类 (图 1c和图 2c)。
因此,在解决实际问题时,应根据研究对象的特点和各种方法的数学性质,选择最适宜的系统聚类方法,同时还需考虑这些方法的专业领域的适用性[13]。
3.2 分类有效性及其类均值差异显著性检验聚类分析的前提是不同类别之间存在显著性差异。如果类与类之间没有显著水平的差别,分类则是无效的。在施肥实践上,如果各类特征肥效方程之间没有显著差异,其指导施肥的针对性和准确性就难以保证。因此,对聚类分析得到的各个类别进行差异显著性检验,是一个不可忽略的技术环节。
本文采用欧氏距离–离差平方和法,将 26 个早稻氮磷钾肥效试验资料的类特征肥效方程分成 3 类。考虑到试验数量只有 26 个,难以满足样点数必须大于产量观测指标数的数理统计一般要求,不可能将各试验点的 14 个处理产量全部纳入统计检验。针对这种情况,傅德印[16]研究指出,可选择对所研究问题密切相关而且具有较强分辨能力的变量作为检验的指标依据,具体可根据实际问题和经验人为地挑选检验指标。为此,本研究选择处理 1 空白区产量和处理 6 平衡施肥产量两个产量指标,作为类别间差异显著性的检验依据。表 3的结果表明,G12、G13 和 G23 的F 值分别为 16.7**、10.9** 和 36.4**,均达到极显著差异,说明分类是有效的。因此,在施肥实践中,可根据空白区产量和平衡施肥产量两个参数,来区分上述 3 个类特征肥效方程。
在诸多聚类分析方法中,系统聚类方法应用最为普遍[12]。它不需要像动态聚类方法那样需要事先人为确定要分成多少类,而是根据系统聚类谱系图和专业知识及实际应用需要,划定某个阈值从而确定分类组别数量,这也是系统聚类方法的优点之一。然而,在应用中盲目套用系统聚类分析方法的情况很多,对不同聚类分析方法的适用性、聚类过程的合理性、聚类结果的有效性等问题分析和重视不够,更谈不上对聚类分析结果进行统计检验[16]。事实上,系统聚类方法是按照聚类步骤并类后得到一张聚类谱系图,该图只反映样本 (或变量) 之间的亲疏关系和程度,其本身并没有给出分类。因此,在划定分类数后,分类结果是否有效?应该进行相应的统计检验,并具体化为分组后的各类之间的均值向量的差异显著性检验[13,16]。
3.3 类特征肥效方程的构建根据欧氏距离–离差平方和的系统聚类分析方法,将仙游县早稻氮磷钾肥效的 26 个试验点分成 3 类。分析表明,这 3 类分别对应于该县的高产、中产和低产稻田类型。根据王兴仁等[3]和毛达如等[1]的建议,将同一个施肥类别内的各试验点求取相同处理产量均值,建立三元二次多项式类特征肥效方程。典型性判别[15]表明,3 个类别的肥效方程均属于典型式,而且 3 类的空白区产量和平衡施肥产量均值有显著差异;在 95% 置信区间下,稻谷产量水平在 3 个类别间几乎不出现交叉重叠,提高了指导早稻合理施肥的可靠性和结果的唯一性。
已有研究表明,当前作物肥效方程出现大量非典型式[15,17–19]。如果完全舍弃这些为数众多的非典型肥效方程的试验结果,不仅造成巨大浪费,而且会造成区域施肥量的估计偏畸[2]。当前,“3414”设计的肥效试验大都采用多点分散不设重复的试验方法,相当于一个随机区组设计。田间肥料试验表明,一个试验点的肥料效应曲线可能出现多种形状,但多点平均效应一般都是抛物线[20]。因此,利用多点试验的相同处理产量均值建立类特征肥效方程的方法,不仅避免了试验信息的偏畸,而且为经济施肥量的计算提供了可能,从而使多点试验资料真正起到施肥决策的依据。
| [1] |
毛达如, 张承东. 多点肥料效应函数的动态聚类方法[J].
北京农业大学学报, 1991, 17(2): 49–54.
Mao D R, Zhang C D. Dynamic clustering method of multipoint fertilizer response function[J]. Journal of Beijing Agricultural University, 1991, 17(2): 49–54. |
| [2] | Colwell J. D. The derivation of fertilizer recommendations for crop in non-uniform environment[J]. Fertilizer, Crop Quality and Economy, 1974, : 936–961. |
| [3] |
王兴仁, 陈伦寿, 毛达如, 等. 分类回归综合法及其在区域施肥决策中的应用[J].
土壤通报, 1989, 20(1): 17–21.
Wang X R, Chen L S, Mao D R, et al. Classification regression synthesis method and its application for regional fertilization decision-making[J]. Chinese Journal of Soil Science, 1989, 20(1): 17–21. |
| [4] |
杨守春, 陈伦寿, 刘光崧, 等. 黄淮海平原主要作物优化施肥与土壤培肥研究总论, 黄淮海平原主要作物优化施肥与土壤培肥技术[M]. 北京: 中国农业科学出版社, 1991. 1—26.
Yang S C, Chen L S, Liu G S,et al. Summary of main crop optimized fertilization and soil fertility improvement in the Huang-Huai-Hai Plain: Technique of main crop optimized fertilization and soil fertility improvement in the Huang-Huai-Hai Plain [M]. Beijing: China Agricultural Science Press, 1991. 1—26. |
| [5] |
吴良欢, 陶勤南. 水稻肥料多点试验聚类分析阈值及其应用[J].
中国水稻科学, 2000, 14(3): 144–148.
Wu L H, Tao Q N. Threshold of cluster analysis for rice dispersed fertilizer experiments and its application[J]. Chinese Journal of Rice Science, 2000, 14(3): 144–148. |
| [6] |
陈欢, 曹承富, 张存岭, 等. 基于主成分-聚类分析评价长期施肥对砂姜黑土肥力的影响[J].
土壤学报, 2014, 51(3): 609–617.
Chen H, Cao C F, Zhang C L, et al. Principal component cluster analysis of effects of long-term fertilization on fertility of lime concretion black soil[J]. Acta Pedologica Sinica, 2014, 51(3): 609–617. |
| [7] | Jalali M. Multivariate statistical analysis of potassium status in agricultural soils in Hamadan, Western Iran[J]. Pedosphere, 2010, 20(3): 293–303. DOI:10.1016/S1002-0160(10)60017-3 |
| [8] | Jin X H, Yao Y H, Liu W L. Principal component analysis and cluster analysis of soil nutrients for planting Schisandrachinensis (Turcz) Baoll in Yanbian Area[J]. Medicinal Plant, 2011, 2(6): 1–4. |
| [9] | Tagarakis A, Liakos V, Fountas S. Management zones delineation using fuzzy clustering techniques in grapevines[J]. Precision Agriculture, 2013, 14: 18–39. |
| [10] | Chen F W, Chen W Y, Liu F J. Improvement of the agricultural effective rainfall for irrigating rice using the optimal clustering model of rainfall station network[J]. Paddy Water Environment, 2014, 12: 393–406. |
| [11] |
鲁如坤. 土壤农业化学分析方法[M]. 北京: 中国农业科技出版社, 2000. 146—196.
Lu R K. Soil agricultural chemical analysis method [M]. Beijing: China Agricultural Science and Technology Press, 2000. 146—196. |
| [12] |
袁志发, 宋世德. 多元统计分析(第二版)[M]. 北京: 科学出版社, 2009. 278—293.
Yuan Z F, Song S D, Multivariate statistical analysis (the second edition) [M]. Beijing: Science Press, 2009. 278—293. |
| [13] |
刘多森, 曾志远. 土壤和环境研究中的数学方法和建模[M]. 北京: 农业出版社, 1987. 134—165.
Liu D S, Zeng Z Y. Mathematical method and modeling of soil and environment [M]. Beijing: Agriculture Press, 1987. 134—165. |
| [14] |
陈彦光. 基于 MATLAB 的地理数据分析[M]. 北京: 高等教育出版社, 2012. 159—180.
Chen Y G. Geographic data analysis based on the MATLAB [M]. Beijing: Higher Education Press, 2012. 159—180. |
| [15] |
章明清, 林代炎, 林仁埙, 姜永. 极值判别分析在三元肥效模型推荐施肥中的作用[J].
福建农业学报, 1995, 10(2): 54–59.
Zhang M Q, Lin D Y, Lin R X, Jiang Y. Function of distinguish analysis on extreme value in recommendatory fertilization for three-fertilizer efficiency model[J]. Fujian Journal of Agricultural Sciences, 1995, 10(2): 54–59. |
| [16] |
傅德印. Q型系统聚类分析中的统计检验问题[J].
统计与信息论坛, 2007, 22(3): 10–14.
Fu D Y. Statistical test problem at Q-mode hierarchical cluster analysis[J]. Statistics & Information Forum, 2007, 22(3): 10–14. |
| [17] |
王兴仁, 等. 二元二次肥料效应曲线等产线图在科学施肥中的位置(一)[J].
土壤通报, 1985, 16(1): 30–34.
Wang X R. The position of yield contour chart of binary quadratic curve of fertilizer response such as production position in scientific fertilization (1)[J]. Chinese Journal of Soil Science, 1985, 16(1): 30–34. |
| [18] |
王兴仁, 等. 二元二次肥料效应曲线等产线图在科学施肥中的位置(二)[J].
土壤通报, 1985, 16(2): 86–88.
Wang X R. The position of yield contour chart of binary quadratic curve of fertilizer response such as production position in scientific fertilization (2)[J]. Chinese Journal of Soil Science, 1985, 16(2): 86–88. |
| [19] |
章明清, 徐志平, 姚宝全, 等. Monte Carlo 法在多元肥效模型参数估计和推荐施肥中的应用[J].
植物营养与肥料学报, 2009, 15(2): 366–373.
Zhang M Q, Xu Z P, Yao B Q, et al. Using Monte Carlo method for parameter estimation and fertilization recommendation of multivariate fertilizer response model[J]. Plant Nutrition and Fertilizer Science, 2009, 15(2): 366–373. |
| [20] |
李娟, 章明清, 姚宝全, 等. 福建单季稻氮磷钾推荐施肥量研究[J].
福建农业学报, 2015, 30(10): 933–938.
Li J, Zhang M Q, Yao B Q, et al. Recommended N, P and K fertilization for single-cropping rice in fujian[J]. Fujian Journal of Agricultural Sciences, 2015, 30(10): 933–938. |
 2017, Vol. 23
2017, Vol. 23  doi:
doi: 

