| 优化法与贝叶斯估计法在非饱和水力参数反演中的比较 |
了解非饱和土壤中水分的运动在农业生产、环境保护等方面具有十分重要的意义.土壤水分运动方程, 即Richards方程[1], 可以描述土壤中水分的运动规律.目前, 研究者已经开发出了很多用于非饱和土壤中水分溶质运移的数值模型, 其中影响力最大, 使用最广泛的是HYDRUS模型[2].HYDRUS模型综合考虑了水分运动、热量迁移、溶质运移、气体运移、化学反应、作物吸收等多个复杂的过程, 而且可以处理各种复杂初始与边界条件下的一维到三维的问题[3-4].介于上述原因, 本研究也采用HYDRUS来进行非饱和土壤水分运动过程的模拟.
运用非饱和土壤水分运动方程进行合理预测的前提是非饱和水力参数的准确获取.但在实际中, 这些参数往往难以直接测量, 需要从更容易获取的水分状态(例如水头和含水量等)中反演得到.此外, 这些参数往往具有空间变异性[5], 为参数的准确反演带来了难度.
传统的参数反演方法大多基于优化算法.以HYDRUS为例, 其自带的参数反演工具是基于Levenberg-Marquardt (LM)非线性优化算法, 已经得到广泛的应用.但这种反演方法都只能给出1组最优解, 无法对内在的不确定性进行量化.此外, 该组解也可能是局部最优解, 而非全局最优解.为了对参数不确定性进行准确的量化, 可以采用随机的参数估计方法.近年来, 在土壤水力特性参数估计领域, 应用最为广泛的2种方法是集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)[6]和马尔科夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)[7].前者基于最优线性估计理论, 后者基于贝叶斯参数估计理论.
在贝叶斯框架下, 所有的待定参数都被视为随机变量, 都用一个相应的分布函数(也称为概率密度函数)来表征[8].当贝叶斯原理用于参数估计时, 观测数据对模型与参数的影响由后验分布来表示.在获得观测数据后, 关于模型参数的统计信息, 如常用的均值、方差、分位值、置信区间等都可以从后验分布得到.然而当系统复杂且非线性时, 往往不存在后验分布的解析式,于是较常用的一种方法是直接生成满足后验分布的样本[9].最常用的方法是MCMC[10].近年来比较流行的高效MCMC算法包括DRAM[11], DREAM[12].MCMC算法在水资源领域中获得了非常广泛的应用, 已有研究者利用MCMC算法来估计土壤水力特性的参数.例如JASPER,等[13]分析了土壤水力特性参数的先验分布对MCMC反演效果的影响.
目前,已有的研究通常只针对均质非饱和水流问题, 即非饱和水力参数在空间上保持不变.而实际中的孔隙介质则可能是分层甚至空间上连续性变化.同时, 也缺乏在孔隙介质异质下贝叶斯参数估计方法与传统优化方法的比较研究.本文研究分层异质时非饱和水流问题中的参数反演问题, 通过数值模拟与沙柱实验, 对比研究贝叶斯MCMC方法与传统的LM优化参数反演方法.
1 材料与方法 1.1 实验材料< 0.25 mm,0.25~0.35 mm,0.35~0.5 mm 3种粒径的沙子,树脂玻璃制作的沙柱柱体,100 mL标准环刀,电子天平,秒表,温度计,热熔胶等.
1.2 实验方法本实验通过图 1所示装置, 模拟水分在一维沙柱中的入渗过程.
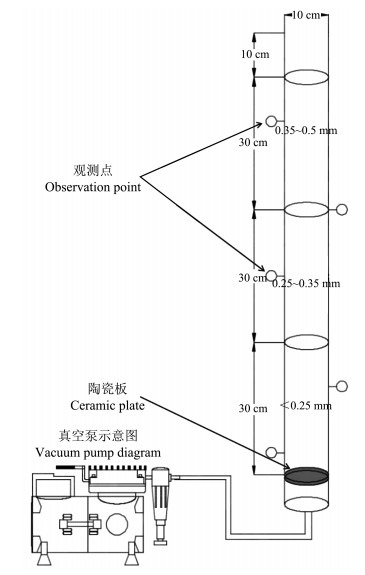 |
| 图1 沙柱装置图 Fig. 1 Sketch of the sand column setup |
沙柱的柱体为树脂玻璃制作而成.其内径为10 cm, 高度100 cm, 柱子底部装有陶瓷板(饱和导水率:0.065 3 cm/d; 厚度:0.714 cm); 沙柱由 < 0.25 mm, 0.25~0.35 mm, 0.35~0.5 mm粒径的沙子自下而上填装, 每层厚度为30 cm.沙柱的填装密度见表 1.
| 表1 不同粒径沙子的饱和水力参数 Table 1 Saturated hydraulic properties of sand with different particle sizes |
 |
| 点击放大 |
根据沙柱各层的填装密度填装环刀样, 并按以下方法测定环刀样的饱和含水量、饱和导水率.
用电子天平称取烘干后的填装环刀质量以及滤纸质量(m1), 再将其放置在水中浸泡24 h, 此时环刀中土壤充满水, 用毛巾擦掉环刀外沾水, 立即称质量(m2).
饱和含水量/%=(m2-m1)/(ρ水×V)×100.
式中:ρ水为水的密度,V为环刀容积.根据计算好的填装密度填装环刀,在环刀上再套1个空的环刀, 接口处用热熔胶封好, 防止水分从接口处漏出, 在环刀土表放1张大小适中的滤纸, 再将其放置在水中浸泡24 h, 此时环刀中土壤充满水.取出后将其放在漏斗上, 漏斗下用50-mL烧杯盛接并向环刀内加水, 水层厚度保持为5 cm.加水后待渗透速率接近稳定开始计时接水, 不同样品设置不同的时间间隔, 同时注意维持水头高相同(5 cm).最后测定水温.当3次读数一样时, 判定为饱和导水率.同一样品做3次平行实验.
饱和导水率=[10×稳定水量×水柱高度(即环刀高)]/时间间隔×环刀横截面积×[水头高度(水层高)+土柱高度].
测得环刀样的饱和含水量和饱和导水率的数据见表 1.
水分入渗试验从上部注水, 在柱子侧边距沙柱表面10、30、45、70和85 cm处设置水头观测点; 下端开口, 用于出水和连接真空泵.
水头通过陶土头和压力传感器(Honeywell 26PCBFA6G)组装起来测得.张力计陶土头部分进气值为30 kPa, 压力传感器的精度为0.4%.因此张力计的量程为-30~30 kPa, 测量精度为0.4%.压力传感器与数据采集器相连, 每10 min自动采集1次各观测点的水头值.
沙柱下端的负压设置分为恒压和变压2种处理.恒压处理下, 在下边界处由真空泵不断抽气, 提供1个恒定的负压(-21.4 kPa), 整个过程时长为76 h; 在变压处理下, 实验的总时长为60 h, 其下边界的负压随时间变化情况见图 2.
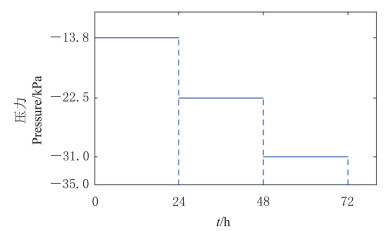 |
| 图2 沙柱下边界负压随时间变化 Fig. 2 Temporal evolution of the vacuum pressure at the lower boundary of the sand column |
实验设计为一维沙柱, 因此所选用的模型均为一维模型.控制方程(Richards方程)描述了土壤中水分的运动过程, 形式如下:
| $ \frac{{\partial \theta \left( h \right)}}{\partial } = \frac{\partial }{{\partial z}}\left[{K\left( h \right)} \right]\frac{{\partial h}}{{\partial z}}\left. { -K\left( h \right)} \right] -S\left( h \right). $ |
式中:θ为容积含水量, cm3/cm3; h为压力水头, cm; K(h)为非饱和导水率,cm/min; z表示垂向深度,cm; t为时间, min; S是源汇项, 1/min.Richards方程描述土壤中含水量与水头随时间的变化关系.为求解该方程, 还需要知道含水量与水头之间的关系, 以及非饱和导水率与水头之间的关系, 即VAN GENUCHTEN-Mualem (VGM)模型.
| $ \theta \left( h \right) = \left\{ {\begin{array}{*{20}{c}} {{\theta _{\rm{r}}} + \frac{{{\theta _{\rm{s}}}-{\theta _{\rm{r}}}}}{{{{\left( {1 + {{\left| {\alpha h} \right|}^n}} \right)}^m}}}, h < 0}\\ {{\theta _{\rm{s}}}, h \ge 0} \end{array};} \right. $ |
| $ K\left( h \right) = \left\{ {\begin{array}{*{20}{c}} {{K_{\rm{s}}}{S_{\rm{e}}}^{1/2}\left[{1-{{\left( {1-{S_{\rm{e}}}^{1/m}} \right)}^m}} \right], h < 0}\\ {{K_{\rm{s}}}, h \ge 0} \end{array}} \right.; $ |
| $ {S_{\rm{e}}} = \frac{{\theta-{\theta _{\rm{r}}}}}{{{\theta _{\rm{s}}}-{\theta _{\rm{r}}}}}; $ |
| $ m = 1-1/n. $ |
式中:α为和平均粒径大小有关的参数; n为和粒径均匀性有关的参数;Se为有效饱和度[14].在给定的边界条件和初始条件下, HYDRUS利用有限元法数值求解Richards方程.本文中, 需要反演的参数为θs(饱和含水量)、θr(残余含水量)、α、n、Ks(饱和导水率).
2.2 反演方法在基于优化的反演算法中, 首要一步是定义一个目标函数Φ, 可表示为:
| $ \Phi \left( {\beta, h} \right) = \sum\limits_{i = 1}^n {{\omega _i}{{\left[{h_i^*\left( {z, t} \right)-{h_i}\left( {z, t, \beta } \right)} \right]}^2}.} $ |
式中:Φ为目标函数;β为待估计参数; h为模型预测值; w为权重因子;h*为实测值;z为垂向深度坐标;t为时间.当选取合适的权重后, 利用Levenberg-Marquardt非线性优化算法调整参数, 使得实测值与模型预测值的差值最小, 可获得目标函数的最小值, 此时对应的参数即为反演结果.该方法只能给出1个结果, 无法量化内在的不确定性.在贝叶斯框架下, 所有待定的模型与参数都被视为随机变量, 都用1个相应的分布函数(也称为概率密度函数)来表征.当贝叶斯原理用于反演问题时, 观测数据对模型与参数的影响用后验分布来表示.在获得观测数据后, 关于模型参数的统计信息, 如常用的均值、方差、分位值、置信区间等都可以从后验分布得到.贝叶斯原理可表示为
P(m|d)∝P(m)P(d|m).
式中:m为待估计的非饱和水力参数, d为观测到的水头数据, P(m)为获得观测数据前的参数分布函数, 即先验分布(prior), 反映了我们在得到观测值之前对目标参数的认识, 可通过查询文献、地质调查等手段获取, 具有一定的主观性.在信息不够齐全的时候, 可假设为在某个区间内的均匀分布.P(d|m)称为似然比(likelihood), 表示在参数取m时观测值d的分布函数, m与d由模型(这里即Richards方程)联系起来.P(m|d)即为后验分布, 反映了从观测数据中获取信息后对目标参数的更新认识.后验分布是贝叶斯参数估计法里面的核心目标.由于Richards方程具有高度非线性, 即使在未知参数具有简单均匀分布时, 后验分布也无法得到解析解.本文使用最新的MCMC算法, DREAM(ZS), 来生成满足后验分布的参数样本.
3 结果与分析 3.1 数值模拟本算例参照沙柱恒压的实验条件, 从先验范围(表 2)中产生1组参数作为“真实”值输入非饱和水流模型, 在观测时刻点产生相应的水头输出值, 通过对其加入标准差为5 cm的白噪声扰动, 得到1组模拟观测值.分别用LM优化算法和MCMC算法进行参数反演.对于LM算法, 选择在先验范围内随机选取1组参数作为优化搜索的初始值; 对于MCMC算法, 设置最长链条长度为50 000, 选取后面5 000长度的链条进行后验分析.因此, 以计算量衡量, LM约需要70次HYDRUS求解器调用, 计算时间约30 s; MCMC需要50 000次求解器调用, 计算时间约4 h.
| 表2 各层沙子非饱和水力参数先验范围 Table 2 Priori ranges of the unsaturated hydraulic parameters for different sand layers |
 |
| 点击放大 |
MCMC算法和LM优化法反演参数的结果见图 3.红色的实线表示各水力参数的真实值, 蓝色的线表示MCMC得到后验概率分布, 红色的虚线表示用LM优化算法得到的结果, 是一个确定的值.LM优化法得到的反演参数与真实值偏差不稳定, 同时容易限于局部最优.MCMC也同样可以给出具体的估计值.例如, 若选用后验概率分布的最大值作为参数估计值(即最大后验估计, Maximum-a-Posterior MAP估计), 从图 3中可见, 大部分的MAP估计值也较靠近真实参数值.更重要的是, MCMC可以充分量化参数的不确定性,即使最大后验估计值偏离了真实值, 后验分布的主要分布区间(也即置信区间)基本上都能将真实值涵盖其中, 因此可以避免只使用单一反演结果进行预测带来的风险.
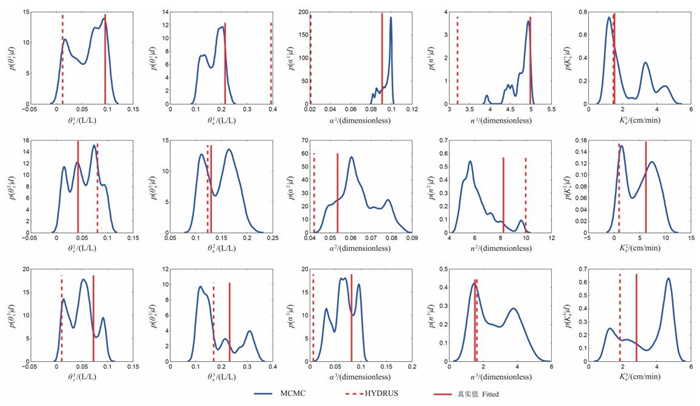 |
| 图3 各层沙体非饱和水力参数反演结果 Fig. 3 Inversion results of hydraulic for different sand layers |
在实际问题中, 由于真实参数都是未知的.另一种判定反演结果准确性的方法是查看使用反演参数值得到水头的预测值和实测值之间的拟合程度.图 4表示不同观测位置处不同反演方法得到的压力水头的预测值随时间的变化关系.红色表示压力水头真实值, 蓝线表示LM优化法对应的预测结果, 而灰色的表示用MCMC反演得到的水头预测值80%的置信区间.可以看出MCMC的反演结果更能将真实值覆盖住, 而LM优化法的结果较MCMC的反演结果, 与实测值偏差较大.因此, MCMC的效果要优于优化算法.
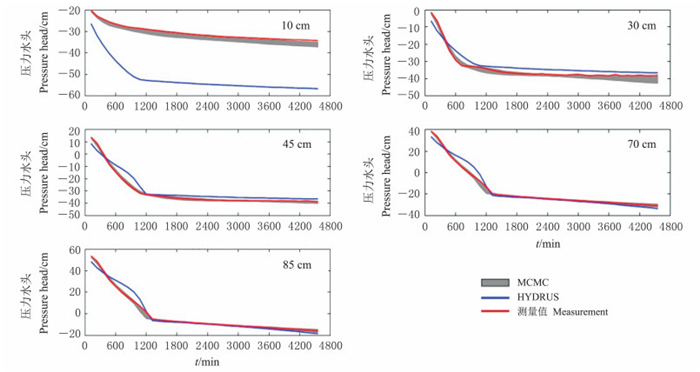 |
| 图4 下边界恒定负压下, 沙柱各观测点压力水头预测值随时间的变化(数值算例) Fig. 4 Temporal evolution of predicted pressure head at measurement locations (numerical case) with the constant vacuum pressure at bottom boundary |
在沙柱实验中, 由于真实参数值未知, 因此无法从参数的后验分布中判定MCMC方法与LM优化法的优劣.利用下边界恒压处理获取的水头观测数据与用MCMC算法对沙柱各层沙的水力参数反演结果见图 5.可以看出, 有些参数的后验分布呈现出明显的多峰分布, 意味着不止一个最优解.因此用MCMC的方法可以有效规避得到一个局部最优解的问题.
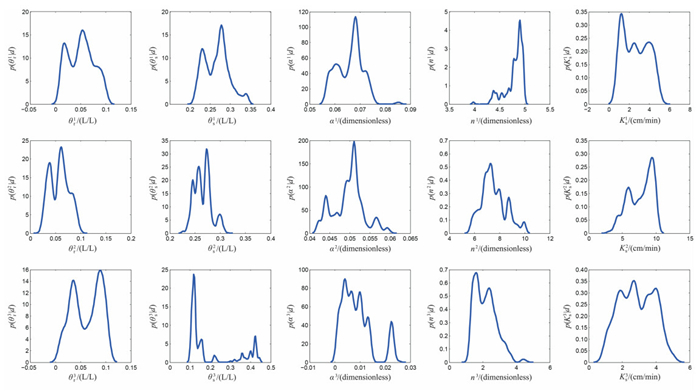 |
| 图5 各参数的后验分布 Fig. 5 Posterior distributions of the parameters |
用MCMC反演出来的参数样本带入模型, 可以得到沙柱恒压实验中压力水头的模拟值, 即图 6中的灰色区域; 红线表示沙柱恒压实验中压力水头的观测值.二者拟合效果很好, 可以认为MCMC反演方法比较可靠.
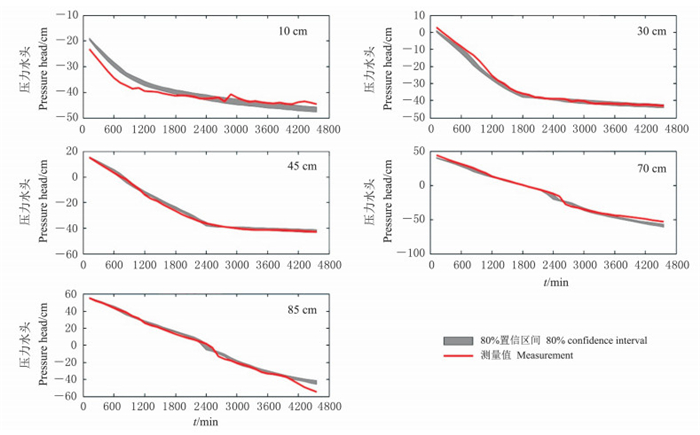 |
| 图6 下边界恒定负压下, 沙柱各观测点压力水头预测值随时间的变化(沙柱试验) Fig. 6 Temporal evolution of predicted pressure head at measurement locations (sand experiment) with the constant vacuum pressure at bottom boundary |
为进一步验证MCMC反演得到的参数在系统外界条件变化时的预测能力, 我们利用下边界变压处理下的压力水头观测值作为校验, 将其与恒压处理下反演参数结果对应的预测值进行对比.如图 7, 红线为压力水头观测值, 灰色区域表示压力水头模拟值80%的置信区间.除10 cm观测点处二者拟合效果不是很好, 其他观测点处拟合性很高.
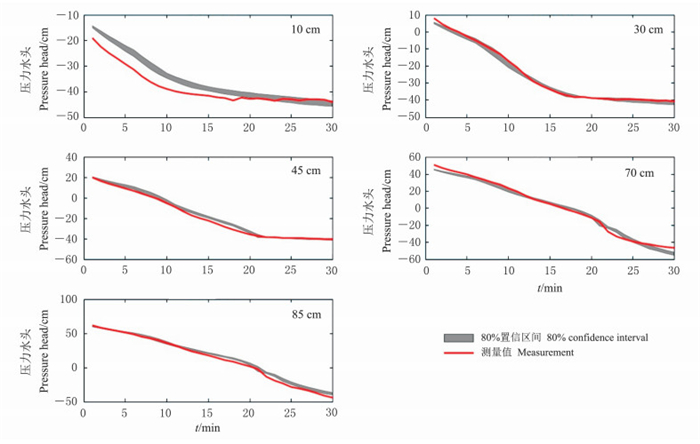 |
| 图7 下边界变化负压下, 沙柱各观测点压力水头预测值随时间的变化(沙柱试验) Fig. 7 Temporal evolution of predicted pressure head at measurement locations (sand experiment) with the changing vacuum pressure at bottom boundary |
对于本研究的多层异质下非饱和水流的反演问题,LM优化方法和MCMC方法都能给出较为合理的结果.
4.2LM优化方法使用广泛,求解速度较快,但受参数初始值影响较大,预测结果与观测值存在一定的偏差,同时由于只能给出一个单一的反演结果,无法量化结果的不确定性.
4.3与基于优化的反演方法相比,MCMC反演方法不仅能够更好地得出参数的单一估计值,同时预测结果与观测值也具有更好的一致性;更重要的是可以给出未知参数的后验分布,从而准确量化非饱和水力参数的不确定性,避免了基于单一参数反演结果进行预测的风险.但是,相对于LM优化方法,MCMC计算量大大增加.
| [1] |
RICHARDS L A. Capillary conduction of liquid sin porous mediums.
Physics, 1931 (1):30–33. |
| [2] | RADCLIFFE D E, SIMUNEK J. Soil Physics with HYDRUS:Modeling and Applications. Boca Raton, FL: CRC Press , 2010 . |
| [3] | SIMUNEK J, HUANG K, VAN GENUCHTEN M T. The HYDRUS-ET Software Package for Simulating the One-Dimentional Movement of Water, Heat and Multiple Solutes in Variably-Saturated Media, Version 1.1. Bratislava: Hydrology Slovak Acad. Sci , 1997 . |
| [4] | SIMUNEK J, SEJNA M, VAN GENUCHTEN M T. HYDRUS-2D:Simulating Water Flow and Solute Transport in Two-dimensional Variably Saturated Media. Golden, Colorado: International Groundwater Modeling Center, Colorado School of Mines , 1996 . |
| [5] |
RUSSO D, BRESLER E. Soil hydraulic properties as stochastic processes:Ⅰ. an analysis of field spatial variability.
Soil Science Society of America Journal, 1981,45 (4):682–687. DOI: 10.2136/sssaj1981.03615995004500040002x. |
| [6] |
EVENSEN G. The ensemble Kalman filter: theoretical formulation and practical implementation.
Ocean Dynamics, 2003,53 (4):343–367. DOI: 10.1007/s10236-003-0036-9. |
| [7] | GILKS W R. Markov Chain Monte Carlo. Wiley Online Library, 2005. |
| [8] | BERNARDO J E M, SMITH A F. Bayesian Theory. John Wiley & Sons, 2009. |
| [9] |
ZHOU H, GOMEZ-HERNANDEZ J J, LI L. Inverse methods in hydrogeology: evolution and recent trends.
Advances in Water Resources, 2014,63 :22–37. DOI: 10.1016/j.advwatres.2013.10.014. |
| [10] | GAMERMAN D, LOPES H F. Markov Chain Monte Carlo:Stochastic Simulation for Bayesian Inference. CRC Press, 2006. https://www.crcpress.com/Markov-Chain-Monte-Carlo-Stochastic-Simulation-for-Bayesian-Inference/Gamerman-Lopes/p/book/9781584885870 |
| [11] |
HAARIO H, LAINE M, MIRA A, et al. DRAM: efficient adaptive MCMC.
Statistics and Computing, 2006,16 (4):339–354. DOI: 10.1007/s11222-006-9438-0. |
| [12] |
VRUGT J A, TER BRAAK C, DIKS C, et al. Accelerating Markov Chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling.
International Journal of Nonlinear Sciences and Numerical Simulation, 2009,10 (3):273–290. |
| [13] |
SCHARNAGL B, VRUGT J A, VEREECKEN H, et al. Inverse modelling of in situ soil water dynamics: investigating the effect of different prior distributions of the soil hydraulic parameters.
Hydrology and Earth System Sciences, 2011,15 (10):3043–3059. DOI: 10.5194/hess-15-3043-2011. |
| [14] |
VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils.
Soil Science Society of America Journal, 1980,44 (5):892–898. DOI: 10.2136/sssaj1980.03615995004400050002x. |
 2016, Vol. 42
2016, Vol. 42


