2. 上海市卫生和健康发展研究中心(上海市医学科学技术情报研究所), 上海 200031;
3. 复旦大学公共卫生学院, 上海 200032;
4. 上海市疾病预防控制中心, 上海 200336;
5. 南通大学医学院医学信息学系, 南通 226001
2. Shanghai Health Development Research Center(Shanghai Medical Information Center), Shanghai 200031, China;
3. School of Public Health, Fudan University, Shanghai 200032, China;
4. Shanghai Municipal Center for Disease Control and Prevention, Shanghai 200336, China;
5. Department of Medical Informatics, Medical School of Nantong University, Nantong 226001, Jiangsu, China
卫生领域的决策者普遍面临着如何将有限的卫生资源合理分配到不同的卫生技术上去的决策难题,这是因为卫生决策过程中会涉及非常多的准则,如:某项卫生技术的效果、成本效果、对预算的影响,某种疾病的发病率、患病率和严重程度,受某种疾病影响的人群亚组,可供选择的替代方案,已有证据的质量等。在比较不同的卫生技术时,决策者通常要根据不同的准则进行选择。多准则决策分析(multi-criteria decision analysis,MCDA)作为一项工具,可以帮助卫生决策者在不同的价值组合中作出取舍。MCDA可以通过一系列的方法,对每一项卫生技术根据其实现决策目标的价值来排名,从而对备选方案从最优到最差进行排序。现概述MCDA的假设基础和基本操作步骤,以期为将MCDA应用于卫生决策提供理论依据。
1 MCDA的产生背景与相关假设MCDA产生于决策者面临至少两个选择时。当决策者在评判某一备选方案时需要考虑几个目标[1],通常不会有一个方案能满足所有目标或全面优于其他方案的情况,每个方案都会在不同水平上满足决策目标,这个时候决策者必定需要作出取舍[2]。MCDA是关于多重目标决策理论的延伸,是将通常互相冲突的准则整合为一个整体的评估方法学,从而对备选方案进行评价[1]。MCDA也可以说是一个笼统的术语,描述了一系列试图在确需考虑多种准则的前提下,帮助个人或团体探索重要决策的正式方法[2]。MCDA旨在帮助决策者更好地评价准则的相关性、重要性,以及利用已有信息来评价备选方案。
MCDA的应用需要基于几个基本假设:①决策者是在有限的资源下作出决策,不是所有的备选方案都能够被采纳,选择一个方案而放弃另一个方案必定会带来机会成本;②决策者的目标是在其个人的自由裁量权之内设定的,而不是由伦理学或经济学的理论规范所决定的[3];③决策者可以对准则赋权重,对备选方案进行评分,并通过准则的多个水平来描述备选方案[4];④决策者可以通过设定准则的相对重要性和准则的取舍,对不同备选方案打分并排序[5]。
2 MCDA模型的构建方法MCDA需要构建一个能够量化决策者偏好或价值判断的模型。尽管MCDA的模型起源于不同理论,但其通常会由两个部分组成:一是决策者针对每个准则表达偏好,二是将描述偏好的准则进行整合,并通过聚合模型进行比较[2]。MCDA模型主要可以分为3类,分别是:价值测量法、优序法和参考模型。
2.1 价值测量法价值测量模型通过构建和比较体现总体价值的分值,从而帮助决策者描述其对某一备选方案相较于另一个备选方案的偏好程度[2]。价值测量模型通常会采用可加模型(或称为“加权求和模型”或“可加多属性价值模型”)。这种模型是将备选方案在每一个准则下的数字得分乘以该准则的相对权重,再将加权后的得分求和后得到每一个备选方案的“总分”。价值测量模型是用于卫生领域决策最常见的MCDA方法[6]。支持价值测量模型的基本理论包括多属性价值理论、多属性效用理论和层次分析法等。
2.2 优序法优序法是通过将备选方案在每一个准则下进行两两比较,将比较结果进行综合后,得到备选方案的总优序数,并按总优序数大小评价备选方案的优劣顺序,排序最前者为所有备选方案中的最优选择。优序法的常见算法包括:消去与选择转换法(elimination and choice expressing reality,ELECTRE)系列方法[7-9]、偏好顺序结构评估法(preference ranking organization methods for enrichment of evaluations,PROMETHEE)系列方法[7]和交互辅助几何分析法(geometrical analysis for interactive aid,GAIA)[8]。目前,优序法尚未被广泛地应用于卫生领域的决策。
2.3 参考模型参考模型的主要方法是决策者预先设定各准则的最低标准,然后对各备选方案进行评分,在所有准则下能够满足最低标准、数量最多的备选方案为最优选择[9]。为了解决满意度的问题,通常会应用线性规划的方法,宗旨是在给定约束条件下达到给定目标的最佳结果。常用的方法有加权目标规划或字典序目标规划。同样,该方法也未被广泛应用于卫生领域的决策。
综上:价值测量模型通过对各准则得分的加权平均得到一个总体分数,以总分来评价备选方案;优序法对备选方案进行成对比较,将比较结果综合起来评价备选方案的优劣;参考模型预先定义各准则的达标标准,寻找与预设标准最接近的备选方案。有研究[10]发现,目前医疗领域内的MCDA有93%选择了价值测量模型的方法[10]。产生这一现象的原因目前并不清楚,但大多数倡导MCDA的机构都推荐使用价值测量模型。
尽管价值测量模型在医疗领域的MCDA中使用更广泛,但对于MCDA模型的选择并没有固定模式,而是应该根据需要决策的问题的本质和目的以及决策者的偏好来决定。在开展MCDA时,决策者应该明确所选择模型与待决策问题的契合度。例如,当决策者认为准则之间具有互补性,即某备选方案在一个准则上的评分虽然较低,但可以通过在另一个准则上的较高得分得到弥补,则该情况下应该使用价值测量模型。原因是价值测量模型通过将各准则得分进行加权求和得到总分,以此评价备选方案。优序法更多地用于需要在一个很大的备选方案集合中选择出一个符合最低标准的备选方案子集的情况,在这种情形下,通过价值测量模型计算所有备选方案的总得分的做法将是非常低效的。
3 MCDA的基本操作步骤为了指导如何将MCDA应用于卫生技术评估(health technology analysis,HTA)及卫生决策,国际药物经济学与结果研究学会(International Society for Pharmacoeconomics and Outcome Research,ISPOR)专门成立了MCDA任务小组。该小组以价值测量法为例,给出了MCDA的具体操作步骤[11],包括:定义决策问题、选择和构建准则、测量备选方案的绩效、对备选方案评分、对准则赋权重、计算加总分数、不确定性分析和结果解读。需要指出的是,MCDA的这些步骤的先后顺序并不是固定不变的。
3.1 定义决策问题MCDA的起点是理解并且定义决策问题和相应的决策目标。同样,这一步也涉及定义合适的利益相关者、备选方案和产出结果。其中,利益相关者可以包括患者、医生、支付方、管理者和大众。利益相关者可以代表他人,也可以是决策者自己。需要决策的问题既可以是一次性的(如选择治疗方案),也可以是重复性的(如HTA机构的报销决策)。
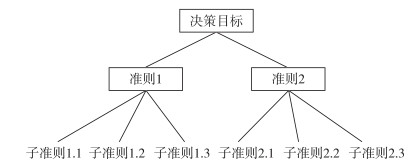
3.2 选择和构建准则明确定义了需要决策的问题后,下一步就要识别评价备选方案的准则,并就准则的选择达成一致。可以通过不同方法确定所需准则,如回顾以往类似决策问题的准则或召集专家会议进行准则的选择等。为了能够用于可加模型,所选取的准则必须满足以下要求[12]:完备性(所有与决策相关的重要准则都包含在内)、非冗余性(避免重复计算准则)、互相独立(准则可以独立地被评价)、可操作性(合适的测量尺度且数据可得)、可聚类(能在概念上以有意义的方式构建准则)。准则确定后就可以通过价值树[13]的方式直观地表示不同准则所处的层级。如图 1所示的价值树,决策目标在最顶部,随着决策者向更低层级移动,需要定义更具体的准则,一直持续到最低级别的准则。
|
图 1 价值树 |
相关准则确定后,就可以通过收集资料来测量备选方案在不同准则上的绩效表现(如收集使用不同药品获得的平均总生存期的差异)。可以通过不同的方法来整合备选方案在每一个准则上的所有绩效数据,如系统回顾或Meta分析,在缺少数据时也可以通过专家意见法获得相应资料。可以将备选方案在不同准则上的绩效收集到一个表格中构成“绩效矩阵”[14]。
3.4 对备选方案评分完成对备选方案绩效资料的收集后,利益相关者就可以对各备选方案进行评分。评分是通过预先设定的规则或函数将绩效测量结果转换为得分。根据测量绩效的不同方法,得分大致可分为2种:一种是将具有不同单位的绩效测量值转换为统一的尺度,如0~100分;另一种则体现了决策者对绩效变化的偏好,决策者对得分相同的绩效变化具有相同的偏好。
获得评分的方法大致可分为“组合”和“分解”两类:组合法是对每一个准则分开考察并生成总体价值,分解法则是将备选方案的总体价值看作一个整体,并从中得到每个准则的权重和得分。
组合法先分开生成权重和得分,再通过MCDA之后的步骤进行组合。如Keeney-Raiffa MCDA方法,将摆幅权重与偏价值函数相结合[15],将备选方案的绩效与其对决策者的价值相联系,从而得到评分。还可以用其他组合法生成得分,例如:直接评分(视觉模拟尺、分配分值)[16]、简单多属性评分技术[17]、成对比较(如层次分析法)[18]、通过分类方法测量属性[19](measuring attractiveness by a categorical based evaluation technique,MACBETH)等。
分解法包括离散选择实验[20]、联合分析[21]和所有备选方案的潜在成对排序[22](potentially all pairwise rankings of all possible alternatives,PAPRIKA)。分解法需要参与者对根据准则定义的真实或假设的备选方案进行排序。以离散选择实验为例,权重和得分是通过回归方法同时获得的,回归系数是备选方案在每一个准则上的变化所对应的绩效或效用的变化。PAPRIKA则是通过基于线性规划的定量方法同时估计权重和得分。
3.5 对准则赋权重赋权重就是要获得利益相关者对不同准则的偏好。权重代表着准则间的取舍,可以把不同准则上的得分整合为一个“总价值”。可以通过不同的方法获得权重,如Keeney-Raiffa MCDA中的摆幅权重法。组合法的其他方法也可以直接生成权重,当然也可以通过分解法离散选择实验或PAPRIKA获得权重。
评分和赋权重通常都是由利益相关者、同时也是决策者来完成的。必须明确谁的偏好与需要决策的问题是相关的,决策的结果对采用了谁的哪一种评分和权重可能会非常敏感。
3.6 计算加总分数在医疗领域的MCDA中更多地会使用价值测量法来进行建模。价值测量模型通常会采用可加模型来计算一个加总分数。如组合法会把备选方案在每一个准则上的得分乘以其权重,再将这些乘积求和得到一个“总价值”。在联合分析或离散选择实验中,将备选方案的绩效数据代入估值函数,就可以通过回归分析估计其价值(或效用)或其能够成为优选方案的可能性。
3.7 不确定性分析不确定性来自于MCDA的设定和输入参数。在MCDA的操作过程中,从准则的设定、绩效测量到评分和赋权重,都会引入不确定性。了解不确定性的存在对于解读MCDA的结果非常重要。可以通过不同的手段分析不同阶段产生的不确定性。例如,参数的不确定性可以进行概率敏感性分析,对模型结构的不确定性可以进行情景分析,还可以通过设定利益相关者亚组的方式了解不同人群偏好的异质性。
3.8 结果解读对MCDA的结果可以进行不同方式的解读,并通过不同的形式呈现给决策者。例如,可以通过加总后的最终得分排序来为备选方案进行重要性或价值排序,备选方案的总得分还可以与成本数据相结合,以确定投资组合或作出关于资源分配的决策。需要强调的是,MCDA是作为一项工具服务于决策者的,最终的决策权属于决策者而不是MCDA。
4 讨论通过MCDA可以提高决策的一致性、透明度和合理性。MCDA已经广泛地应用于交通、教育、投资、环境、国防等领域[11]。MCDA在卫生领域内的应用相对滞后,但随着越来越多的研究者和实践者关注到这一技术,MCDA在卫生领域的应用将日趋增加。截至目前,MCDA已被应用于收益-风险评估、不同HTA机构的决策、卫生资源分配决策等卫生决策领域。在中国的卫生领域内也出现了一些MCDA的应用研究,如:胡善联等[23]运用MCDA方法对“孤儿药”的遴选条件进行分析,并比较了不同利益相关者在遴选罕见病“孤儿药”时对评价标准重要性的排序;胡善联等[24]还将MCDA应用于血友病A的不同治疗方案的综合评价;耿劲松等[25]尝试基于“证据与价值对决策的影响”框架构建新技术的医疗保险报销循证决策框架,探讨将MCDA用于新技术医疗保险报销决策的可行性;徐俊马等[26]探讨如何将MCDA应用于重症肺炎的集束化管理中,从而达到提高决策的科学性、降低医疗费用、改善患者结局和预后的目的;宋子扬等[27]结合HTA与MCDA建立了儿童用药临床综合评价的方法学框架,并以哮喘控制类用药初步验证其可行性。
MCDA应用于卫生决策可以整合多个决策准则,避免根据单一准则作出有偏倚的决策,从而能够有效地提高决策的科学性和稳健性。应该注意的是,MCDA作为一个在决策过程中整合不同观点的平台,所选择的利益相关者的类型和数量会影响到MCDA的决策结果[28]。因此,建立和完善MCDA的相关指南,将每一位利益相关者的个人影响最小化就显得尤为重要。
可以看到,MCDA在中国卫生领域的应用还处于起步和探索阶段。同时应该注意到,由于使用MCDA还存在很多挑战,对于不熟悉MCDA的决策者而言,方法的多样性使得理解和很好地使用MCDA变得非常困难。希望通过对MCDA基本假设、相关模型理论和基本操作步骤的介绍可以帮助卫生领域的决策者了解MCDA,进而能够在将来的决策过程中更好地探索使用这一工具。
·作者声明本文无实际或潜在的利益冲突
| [1] |
KEENEY R L, RAIFFA H. Decisions with multiple objectives preferences and value tradeoffs[M]. Cambridge: Cambridge University Press, 1993: 569.
|
| [2] |
BELTON V, STEWART T J. Multiple criteria decision analysis:an integrated approach[M]. Boston: Springer, 2002: 372.
|
| [3] |
PEACOCK S, MITTON C, BATE A, et al. Overcoming barriers to priority setting using interdisciplinary methods[J]. Health Policy, 2009, 92(2): 124-132. |
| [4] |
LANCASTER K J. A new approach to consumer theory[J]. J Pol Economy, 1966, 74(2): 132-157. DOI:10.1086/259131 |
| [5] |
BALTUSSEN R, NIESSEN L. Priority setting of health interventions:the need for multi-criteria decision analysis[J]. Cost Eff Resour Alloc, 2006, 4(1): 14-18. DOI:10.1186/1478-7547-4-14 |
| [6] |
DOLAN J G. Multi-criteria clinical decision support:a primer on the use of multiple criteria decision making methods to promote evidence-based, patient-centered healthcare[J]. Patient-patient Centered Outcomes Res, 2010, 3(4): 229-248. DOI:10.2165/11539470-000000000-00000 |
| [7] |
BRANS J P, VINCKE P. Note:a preference ranking organization method:the PROMETHEE method for multiple criteria decision-making[J]. Manag Sci, 1985, 31(6): 647-656. DOI:10.1287/mnsc.31.6.647 |
| [8] |
BRANS J P, MARESCHAL B. The PROMCALC & GAIA decision support system for multicriteria decision aid[J]. Decis Support Syst, 1994, 12(4-5): 297-310. DOI:10.1016/0167-9236(94)90048-5 |
| [9] |
AOUNI B, KETTANI O. Goal programming model:a glorious history and a promising future[J]. Eur J Oper Res, 2001, 133(2): 225-231. DOI:10.1016/S0377-2217(00)00294-0 |
| [10] |
MARSH K, LANITIS T, NEASHAM D, et al. Assessing the value of healthcare interventions using multi-criteria decision analysis:a review of the literature[J]. Pharmacoeconomics, 2014, 32(4): 345-365. DOI:10.1007/s40273-014-0135-0 |
| [11] |
THOKALA P, DEVLIN N, MARSH K, et al. Multiple criteria decision analysis for health care decision making:an introduction:report 1 of the ISPOR MCDA emerging good practices task force[J]. Value Health, 2016, 19(1): 1-13. |
| [12] |
DODGSON J, SPACKMAN M, PEARMAN A, et al. Multi-criteria analysis: a manual[EB/OL].[2020-02-02]. https://www.researchgate.net/publication/30529921_Multi-Criteria_Analysis_A_Manual#read.
|
| [13] |
VON WINTERFELDT D, FASOLO B. Structuring decision problems:a case study and reflections for practitioners[J]. Eur J Oper Res, 2009, 199(3): 857-866. DOI:10.1016/j.ejor.2009.01.063 |
| [14] |
EUROPEAN MEDICINES AGENCY, BENEFIT-RISK METHODOLOGY PROJECT. Work package 4 report: benefit-risk tools and processes[EB/OL]. (2012-05-09)[2020-02-02]. http://www.ema.europa.eu/docs/en_GB/document_library/Report/2012/03/WC500123819.pdf.
|
| [15] |
EUROPEAN MEDICINES AGENCY, BENEFIT-RISK METHODOLOGY PROJECT. Work package 3 report: field tests[EB/OL]. (2011-08-31)[2020-02-02]. https://www.ema.europa.eu/en/documents/report/benefit-risk-methodology-project-work-package-3-report-field-tests-en.pdf.
|
| [16] |
BOTTOMLEY P A, DOYLE J R, GREEN R H. Testing the reliability of weight elicitation methods:direct rating versus point allocation[J]. J Mark Res, 2000, 37(4): 508-513. DOI:10.1509/jmkr.37.4.508.18794 |
| [17] |
EDWARDS W. How to use multiattribute utility measurement for social decision making[J]. IEEE Trans Syst Man Cybern, 1977, 7(5): 326-340. DOI:10.1109/TSMC.1977.4309720 |
| [18] |
SAATY T L. A scaling method for priorities in hierarchical structures[J]. J Math Psychol, 1977, 15(3): 234-281. DOI:10.1016/0022-2496(77)90033-5 |
| [19] |
BANAE COSTACA, DE CORTE J M, VANSNICK J C. On the mathematical foundations of MACBETH[M]//FIGUEIRA J, GRECO S, EHROGOTT M, et al. Multiple criteria decision analysis: state of the art surveys. New York: Springer, 2016: 421-463.
|
| [20] |
RYAN M, GERARD K. Using discrete choice experiments to value health care programmes:current practice and future research reflections[J]. Appl Health Econ Health Policy, 2003, 2(1): 55-64. |
| [21] |
GREEN P E, KRIEGER A M, WIND Y. Thirty years of conjoint analysis:reflections and prospects[J]. Interfaces, 2001, 31(S3): S56-S73. |
| [22] |
HANSEN P, OMBLER F. A new method for scoring additive multi-attribute value models using pairwise rankings of alternatives[J]. J Multi-crit Decis Anal, 2008, 15(3-4): 87-107. DOI:10.1002/mcda.428 |
| [23] |
胡善联, 杨燕, 何江江, 等. 罕见病孤儿药遴选标准的多维决策分析[J]. 中国卫生经济, 2018, 37(3): 67-70. |
| [24] |
胡善联, 何江江, 杨燕, 等. 多维度决策分析在血友病预防性治疗中的应用[J]. 中国卫生经济, 2017, 36(9): 55-58. |
| [25] |
耿劲松, 陈晓炜, 余小兰, 等. 基于EVIDEM的新技术医保报销循证决策框架探析[J]. 中国卫生政策研究, 2018, 11(4): 50-54. |
| [26] |
徐俊马, 赵杰, 贾晓民, 等. 多准则决策分析在重症肺炎集束化治疗中的意义[J]. 中华危重病急救医学, 2015, 27(10): 796-799. |
| [27] |
宋子扬, 尉耘翠, 聂晓璐, 等. 基于卫生技术评估联合多准则决策分析建立我国儿童用药临床综合评价方法[J]. 药物流行病学杂志, 2019, 28(10): 681-686. |
| [28] |
KOLASA K, ZAH V, KOWALCZYK M. How can multi-criteria decision analysis support value assessment of pharmaceuticals?:findings from a systematic literature review[J]. Expert Rev Pharmacoecon Outcomes Res, 2018, 18(4): 379-391. DOI:10.1080/14737167.2018.1467759 |
 2020, Vol. 23
2020, Vol. 23


