2. 中国石油辽河油田公司勘探开发研究院
2. Exploration and Development Research Institute of PetroChina Liaohe Oilfeld Company
潜山油气藏是华北油田主要勘探领域之一[1-2]。河间潜山油气藏埋藏深、内幕构造复杂、速度横向变化剧烈,常规的偏移方法难以对潜山内幕进行精确的成像,制约了人们对潜山内幕的认识,增加了勘探开发风险[3]。常规的偏移方法在复杂构造区域成像方面的不足日益凸显,逆时偏移为复杂构造区域精确成像提供了一种可靠的方法。基于双程波动方程的逆时偏移方法克服了传统单程波成像中偏移倾角和偏移孔径的限制,对纵、横向速度剧烈变化的介质适应性强[4]。逆时偏移具有相位准确、成像精度高,以及可以对回转波、多次波、棱镜波成像等优点。
逆时偏移概念最早由Whitemore在第53届SEG年会上提出[5],随后,Levin概括了逆时偏移的基本原理和实现方法[6],标志着逆时偏移技术的初步形成。在使用的波动方程形式方面,Chang等将声波方程逆时偏移推广到了弹性波方程[7];Causse等将弹性波方程逆时偏移推广了粘弹性波动方程[8];Huang和方修政进一步将逆时偏移推广到了各向异性介质[9-10];杜启振等将逆时偏移从单分量推广到了多分量[11]。在差分格式方面,Wu等研究了三维介质的高阶有限差分格式的逆时偏移方法[12];Wang提出了逆时偏移的变时间步长和空间大小的方法[13];方刚等将交错网格Lowrank有限差分格式用于逆时偏移中,并对Marmousi模型进行了成像,证实了该格式的优越性[14]。在计算方面,针对逆时偏移计算量大的问题,Micikevicius给出了利用GPU实现高阶有限差分计算的算法[15];Foltinek等在利用GPU实现逆时偏移的工业化生产方面做了很好的尝试[16];张慧等实现了GPU并行加速的逆时偏移方法,并用实际资料说明了该方法的高效性[17]。在实际应用方面,刘定进等采用高阶有限差分逆时偏移方法对盐下构造进行了成像,取得了良好的效果[18];杨江峰等利用逆时偏移技术对塔西南地区的碳酸盐岩进行了成像,提高了碳酸盐岩内幕“串珠”成像、缝—洞储层刻画的精度[19];王维红等开发了基于Qt平台的VSP逆时偏移软件,该软件具有操作性强、移植性好和成像精度高的优点[20]。
1 方法原理 1.1 高阶有限差分波场外推算法逆时偏移的核心是波场外推问题,波场外推的方法主要有有限差分法、有限元法和伪谱法等[21]。选取一种适应性强、计算精度高、效率高的波场外推方法是逆时偏移的关键。有限差分方法具有实现简单、计算快速灵活、对速度场适应性强的特点,是目前应用最多的波场外推方法。
叠前逆时深度偏移使用常密度声波方程,即:
| $ \frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{y}^{2}}}\text{+}\frac{{{\partial }^{2}}u}{\partial {{z}^{2}}}\text{=}\frac{1}{v}\frac{{{\partial }^{2}}u}{\partial {{t}^{2}}} $ | (1) |
式中u——地下介质的压力场;
v——纵、横向可变的介质速度;
x、y、z——空间坐标。
有限差分方法是对公式(1)中的二阶导数进行离散化处理,用差分代替微分求解波动方程来实现波场外推。
在正向外推和逆时外推中,使用常规差分格式时,为了减弱频散问题和保证计算稳定,通常要求计算网格足够小,网格小会使计算机的内存和计算时间大大增加。采用高阶有限差分格式时,在保证计算精度的前提下,网格可以取得足够大。许多学者都对波动方程的高阶有限差分算法进行了研究[11, 17],本文仅仅给出高阶有限差分的计算公式,即:
| $ \begin{align} &u_{i, j, k}^{n+l}=2u_{i, j, k}^{n}-u_{i, j, k}^{n-1}+ \\ &\frac{1}{2}{{\left( \frac{v\Delta t}{\Delta x} \right)}^{2}}\left[{{\omega }_{0}}u_{i, j, k}^{n}+\sum\limits_{m=1}^{\frac{M}{2}}{{{\omega }_{m}}\left( u_{i+m, j, k}^{n}+u_{i-m, j, k}^{n} \right)} \right]+ \\ &\frac{1}{2}{{\left( \frac{v\Delta t}{\Delta \text{y}} \right)}^{2}}\left[{{\omega }_{0}}u_{i, j, k}^{n}+\sum\limits_{m=1}^{\frac{M}{2}}{{{\omega }_{m}}\left( u_{i, j+m, k}^{n}+u_{i, j-m, k}^{n} \right)} \right]+ \\ &\frac{1}{2}{{\left( \frac{v\Delta t}{\Delta z} \right)}^{2}}\left[{{\omega }_{0}}u_{i, j, k}^{n}+\sum\limits_{m=1}^{\frac{M}{2}}{{{\omega }_{m}}\left( u_{i, j, k+m}^{n}+u_{i, j, k+m}^{n} \right)} \right] \\ \end{align} $ | (2) |
式中i、j、k、n——分别为空间x、y、z方向和时间
t方向上的离散网格点;
M——空间阶数;
ω——差分系数;
Δx、Δy、Δz、Δt、——分别为空间x、y、z方向和时间t方向的步长。
使用时间2阶、空间10阶格式,此时差分系数分别为:ω0 =-5.854444,ω1 =3.333333,ω2 =-0.476190,ω3 =0.079365,ω4 =-0.009921,ω5 =0.000635。
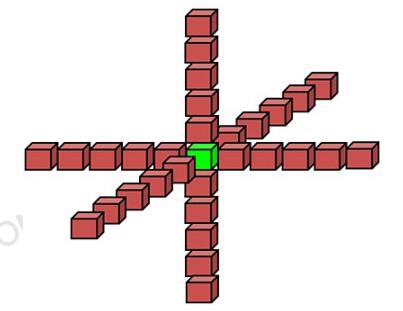
公式(2)的含义是,计算空间某点n+1时刻的波场时,需要用到该点n时刻和该点周围30个点的n-1时刻的波场。这31个点的位置关系如图 1所示。公式(2)给出了正向外推的计算公式,逆时外推的公式可以由公式(2)得到,本文不再赘述。
|
图 1 高阶有限差分格式 |
公式(1)描述了地震波在地下无限区域内传播的情况,而实际外推的区域是有限的,这就相当于在外推区域的边界引入了一个人为的反射界面,它会产生强烈的边界反射干扰。因此必须构造边界条件,使边界产生的反射尽量少,这样才能使外推过程不受边界反射的影响。
本文采用声波方程完全匹配层吸收边界[18],其具体思想是在外推区域的边界增加吸收层,地震波由研究区域边界传播到吸收层是不产生反射的,从而使地震波在吸收层内按传播距离的指数规律衰减,以达到减少边界反射的效果。其具体计算公式如下:
| $ \left\{ \begin{align} &{{\left( {{\partial }_{t}}+\beta \right)}^{2}}{{u}_{1}}={{v}^{2}}\frac{{{\partial }^{2}}u}{\partial {{x}^{2}}} \\ &{{\left( {{\partial }_{t}}+\beta \right)}^{3}}{{u}_{2}}=-{{v}^{2}}\beta \frac{\partial u}{\partial x} \\ &{{\partial }_{t}}{{u}_{3}}={{v}^{2}}\left( \frac{{{\partial }^{2}}u}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{z}^{2}}} \right) \\ \end{align} \right. $ | (3) |
式中u1、u2、u3——压力场u分裂成的3个部分;
β——边界衰减因子。
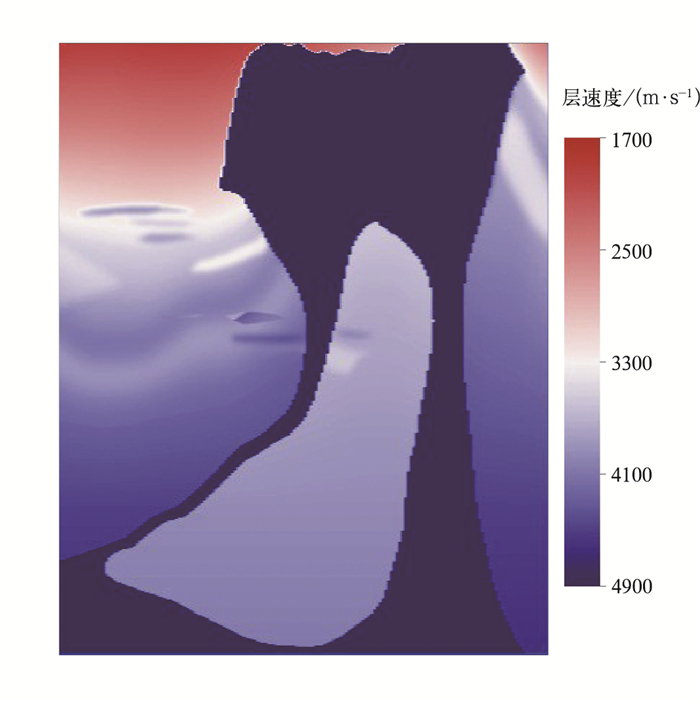
2 理论模型测试为了测试算法的应用效果,使用BP公司2004年发布的标准模型进行试算。图 2为标准模型中间部位盐丘的速度模型。图 2中的盐丘与其周围的地层速度差异较大,且埋藏较深,盐丘内部含有其他岩体,这些特点与潜山及潜山内幕的特征具有很大相似性,所以选择图 2中的模型来测试本文算法。模型数据体的模拟参数为:共1340炮,炮间距为50m,每炮1201道接收,道间距为12.5m,采样时间为14min,采样间隔为6ms,子波主频为27Hz,网格大小为6.25m×6.25m。
|
图 2 速度模型 |
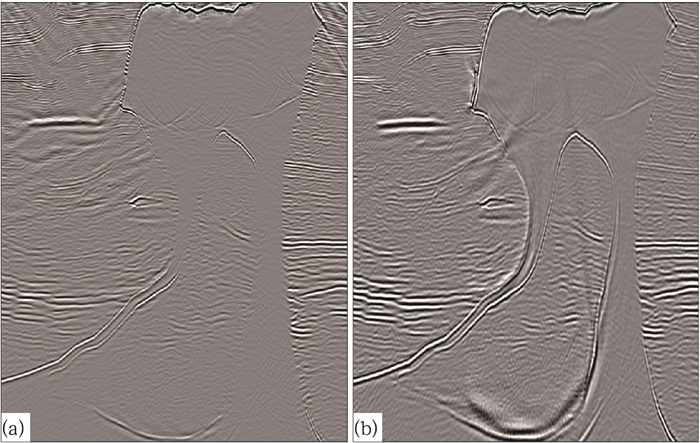
图 3a为单程波动方程叠前深度偏移剖面,可以看到,平缓地层的成像比较清楚,盐丘的大体形态可见,但是边界成像不清楚,尤其是左侧陡倾角的地方,更为严重的是盐丘内幕岩体几乎不成像。图 3b为逆时偏移剖面,该剖面中地层成像清楚,盐丘及盐丘边界成像准确,盐丘内幕岩体成像清楚。综合可知,逆时偏移对陡构造和内幕构造的成像效果要优于单程波动方程叠前深度偏移。
|
图 3 理论模型偏移结果对比 (a)单程波动方程叠前深度偏移;(b)逆时偏移 |
河间潜山构造带隶属于饶阳凹陷东部陡带,受留路—河间基底大断层控制,在大断层上升盘形成隆升带,潜山断层下降盘为河间主生油洼槽,油源条件好。潜山走向为北东向,潜山出露地层由西北向东南由老变新,西北断面出露古元古界花岗片麻岩,向东南依次出现中元古界长城系常州沟组、团山子组、串岭沟组、高于庄组、杨庄组、雾迷山组,地层走向北东东向,倾向南东向。现已发现河间高于庄组层状潜山油藏和常州沟组内幕油藏。潜山内幕地层埋藏较深,潜山内幕构造复杂,潜山内幕资料信噪比低,给潜山内幕精确成像和构造展布特征的落实带来了极大困难。
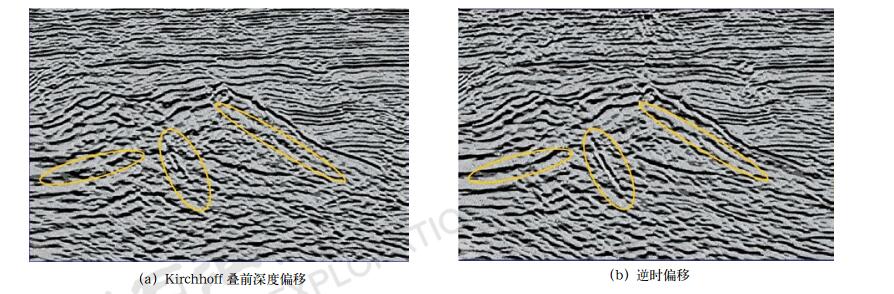
采用传统的Kirchhoff叠前深度偏移方法和本文的逆时偏移方法,对河间潜山地震资料进行了处理。图 4为使用网格层析法进行多次迭代之后获得的层速度模型。图 5为利用上述速度模型使用Kirchhoff叠前深度偏移和逆时偏移得到的剖面,显示的是联络测线方向。可以看出,两种方法对中浅层起伏比较小的地层都能正确成像,且对潜山边界的刻画也比较准确,但是对潜山内幕的成像差别比较明显。Kirchhoff叠前深度偏移剖面中内幕信噪比低,内幕地层连续性差,断面、断点不清楚;逆时偏移剖面中内幕信噪比、分辨率明显提高,内幕地层连续性增强,波组特征更加清楚,易于追踪,断层归位准确,断面干脆,断点清晰。综合可知,逆时偏移对潜山内幕成像具有明显的优势,其成像效果和成像质量明显好于Kirchhoff叠前深度偏移。

|
图 4 河间潜山深度域层速度剖面 |
|
图 5 Kirchhoff叠前深度偏移和逆时偏移实际资料剖面对比 |
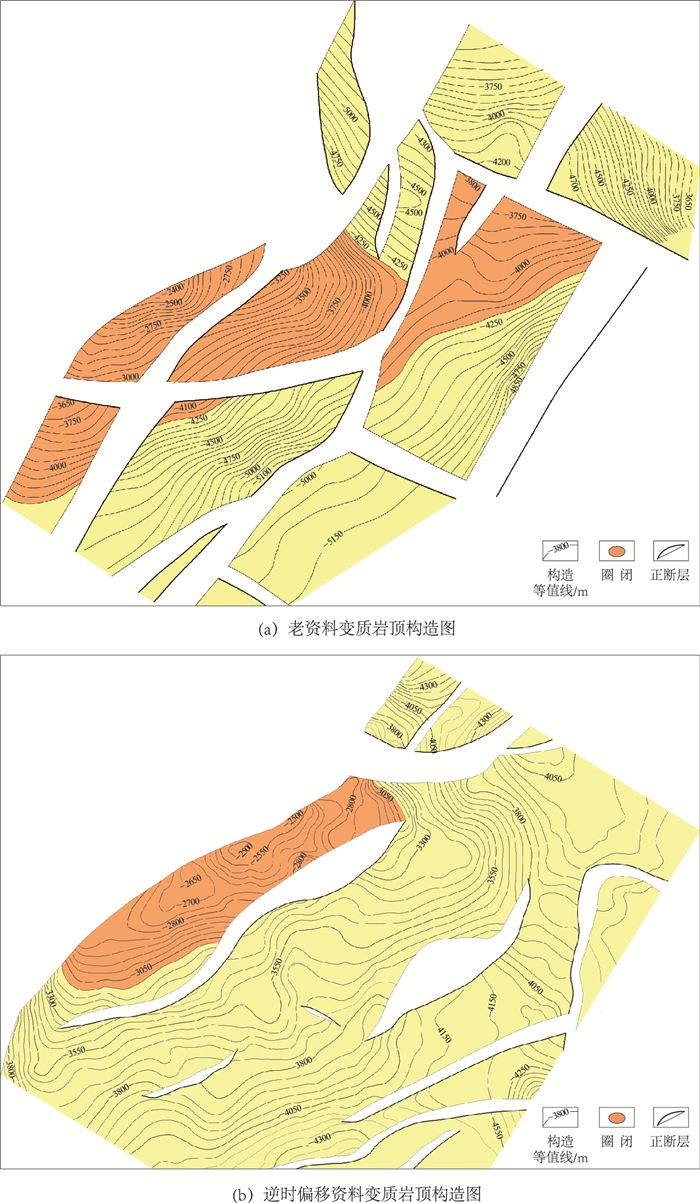
为了进一步说明文中逆时偏移方法的应用效果,将逆时偏移资料的河间潜山内幕变质岩顶构造图和老资料进行了对比(图 6),可以看出,逆时偏移资料变质岩顶构造图中鼻状构造形态更加完整,构造细节更加精确,识别处理了两个构造高点。
|
图 6 河间潜山内幕变质岩顶构造图 |
潜山内幕油气藏是当前潜山型油气藏勘探的主要研究方向之一,潜山内幕的精确成像是一大难题。本文采用高阶有限差分逆时偏移方法,实现了对构造复杂的潜山内幕的高精度成像,并且形成了一套适用于潜山内幕成像的处理技术。对比分析逆时偏移与传统叠前深度偏移的成像效果可知,逆时偏移对构造复杂的潜山内幕的成像效果优于传统的单程波动方程叠前深度偏移和Kirchhoff叠前深度偏移。
| [1] |
赵贤正, 田福清, 王权, 范炳达, 董雄英, 赵淑芳, 等. 老区富油凹陷"五精一创"勘探实践与启示[J].
中国石油勘探, 2016, 21(6): 1–8.
Zhao Xianzheng, Tian Fuqing, Wang Quan, Fan Bingda, Dong Xiongying, Zhao Shufang, et al. Application and performance of delicate and innovative exploration practices in oil-rich sags of matured areas[J]. China Petroleum Exploration, 2016, 21(6): 1–8. |
| [2] |
吴伟涛, 高先志, 李理, 张东伟, 刘宝. 渤海湾盆地大型潜山油气藏形成的有利因素[J].
特种油气藏, 2015, 22(2): 22–26.
Wu Weitao, Gao Xianzhi, Li Li, Zhang Dongwei, Liu Bao. Favorable conditions formed in large-scale buried-hill reservoir in Bohai Bay Basin[J]. Special Oil & Gas Reservoirs, 2015, 22(2): 22–26. |
| [3] |
崔永谦, 王永刚, 杜维良, 白博, 王红. 任丘潜山内幕特征描述及储层预测研究[J].
石油物探, 2010, 49(3): 280–286.
Cui Yongqian, Wang Yonggang, Du Weiliang, Bai Bo, Wang Hong. Interior characteristics description and reservoir prediction of Renqiu buried hill[J]. Geophysical Prospecting for Petroleum, 2010, 49(3): 280–286. |
| [4] |
高厚强, 徐颖, 邵文潮, 穆洁, 蒋波, 陈哲. 逆时偏移技术在碳酸盐岩缝洞体成像中的应用[J].
中国石油勘探, 2017, 22(1): 99–105.
Gao Houqiang, Xu Ying, Shao Wenchao, Mu Jie, Jiang Bo, Chen Zhe. Application of reverse-time migration technology in imaging of fractures and cavities in carbonate reservoirs[J]. China Petroleum Exploration, 2017, 22(1): 99–105. |
| [5] | Whitemore N D.Iterative depth migration by back-ward time propagation[C].Expanded Abstracts of 53rd SEG Annual International Meeting, 1983:382-384. |
| [6] | Levin S A. Principles of reverse time migration[J]. Geophysics, 1984, 49(5): 581–583. DOI:10.1190/1.1441693 |
| [7] | Chang W F, McMechan G A. 3D elastic prestack reverse-time depth migration[J]. Geophysics, 1994, 59(4): 597–609. DOI:10.1190/1.1443620 |
| [8] | Causse E, Ursin B. Viscoacoustic reverse-time migration[J]. Journal of Seimic Exploration, 2000, 9(1): 165–184. |
| [9] | Huang T, Zhang Y, Zhang H Z, Yong J. Subsalt imaging using TTI reverse time migration[J]. The Leading Edge, 2009, 28(4): 448–452. DOI:10.1190/1.3112763 |
| [10] |
方修政, 石颖, 柯璇, 高新成, 井洪涛. VTI介质高精度叠前逆时偏移方法研究[J].
地球物理学进展, 2015, 30(4): 1677–1684.
Fang Xiuzheng, Shi Ying, Ke Xuan, Gao Xincheng, Jing Hongtao. Investigation on high-accuracy pre-stack reversetime migration for VTI medium[J]. Progress in Geophysics, 2015, 30(4): 1677–1684. DOI:10.6038/pg20150422 |
| [11] |
杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移[J].
地球物理学报, 2009, 52(3): 801–807.
Du Qizhen, Qin Tong. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium[J]. Chinese Journal of Geophysics, 2009, 52(3): 801–807. |
| [12] | Wu W, Lines L R, Lu H. Analysis of higher-order, finite-difference schemes in 3D reverse-time migration[J]. Geophysics, 1996, 61(3): 845–856. DOI:10.1190/1.1444009 |
| [13] | Yue Wang.Reverse-time migration by a variable time-step and space-grid method[C].Expanded Abstracts of 70th SEG Annual International Meeting, 2000:798-801. |
| [14] |
方刚, FomelSergey, 杜启振. 交错网格Lowrank有限差分及其在逆时偏移中的应用[J].
中国石油大学学报, 2014, 38(2): 44–51.
Fang Gang, Fomel Sergey, Du Qizhen. Lowrank finite difference on a staggered grid and its application on reverse time migration[J]. Journal of China University of Petroleum, 2014, 38(2): 44–51. |
| [15] | Micikevicius P. 3D finite difference computation on GPUs using CUDA[C].Expanded Abstracts of 2nd Workshop on general purpose processing on Graphics processing units, 2009:79-84. |
| [16] | Foltinek D, Eation D, Mahovsky J, Moghaddam P, Mcgarrg R. Industrial-scale reverse time migration on GPU hardware[C]. Expanded Abstracts of 80th SEG Annual International Meeting, 2010:2789-2793. |
| [17] |
张慧, 蔡其新, 秦广胜, 高爱荣, 林玉英. GPU并行加速的多步逆时偏移在东濮前梨园地区的应用[J].
物探与化探, 2015, 39(1): 161–165.
Zhang Hui, Cai Qixin, Qin Guangsheng, Gao Airong, Lin Yuying. The application of GPU accelerated multi-step reverse time migration to Qianliyuan area in Dongpu[J]. Geophysical and Geochemical Exploration, 2015, 39(1): 161–165. DOI:10.11720/wtyht.2015.1.26 |
| [18] |
刘定进, 杨勤勇, 方伍宝, 孔祥宁, 张慧宇. 叠前逆时深度偏移成像的实现与应用[J].
石油物探, 2011, 50(6): 545–549.
Liu Dingjin, Yang Qinyong, Fang Wubao, Kong Xiangning, Zhang Huiyu. Realization and practices of prestack reverse-time depth migration[J]. Geophysical Prospecting for Petroleum, 2011, 50(6): 545–549. |
| [19] |
杨江峰, 刘定进, 朱文斌, 关达, 胡中平, 王汝珍, 等. 逆时偏移技术在碳酸盐岩缝-洞储层成像中应用[J].
高校地质学报, 2014, 20(2): 303–308.
Yang Jiangfeng, Liu Dingjin, Zhu Wenbin, Guan Da, Hu ZhongPing, Wang Ruzhen, et al. Technique and application of reverse time migration of fractured-vuggy carbonate reservoir[J]. Geological Journal of China Universities, 2014, 20(2): 303–308. |
| [20] |
王维红, 柯璇, 郭雪豹, 张莹莹, 余鹏. 基于Qt的Walkaway VSP逆时偏移软件开发研究[J].
石油物探, 2015, 54(4): 452–458.
Wang Weihong, Ke Xuan, Guo Xuebao, Zhang Yingying, Yu Peng. Qt based software development of reverse time migration for walkaway VSP seismic data[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 452–458. |
| [21] |
陈可洋. 地震波逆时偏移方法研究综述[J].
勘探地球物理进展, 2010, 33(3): 153–159.
Chen Keyang. Review of seismic reverse time migration methods[J]. Progress in Exploration Geophysics, 2010, 33(3): 153–159. |


