2. 中国科学院大学电子电气与通信工程学院,北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
近年来,遥感卫星虽然空间分辨率得到了提高,但受物理条件和制造工艺的限制,单一的卫星载荷很难同时获取高空间分辨率和高光谱分辨率的光学遥感图像[1]。最常见的光学遥感图像包括全色图像(panchromatic,PAN)和多光谱图像(multispectral,MS)。全色图像拥有丰富的空间细节,但只有一个波段,光谱分辨率较差。多光谱图像对数个波段进行摄取,通常具有很高的光谱分辨率,但受传感器、传输带宽、噪声等限制,多光谱图像的空间分辨率相对有所下降。为使多光谱遥感图像拥有更高的空间清晰度,可基于MS和PAN通过遥感图像锐化[2]方法获得高空间分辨率的MS图像。
经过多年的发展,传统遥感图像锐化算法已经有着丰富的成果,主要包括成分替换法(component substitution, CS)[3]、多分辨率分析法(multi-resolution analysis, MRA)[4]和基于模型的方法[5]。
CS是将多光谱图像转换到高维空间,在高维空间中将多光谱的空间信息成分替换为全色图像。该方法在实现过程中,全色图像与多光谱图像之间相关性越大,则引入的频谱失真就越小。亮度-色度-饱和度变换法[6]、施密特正交化变换法(Gram-Schmidt, GS)[7]、Brovery变换法[8]和主成分分析法[9]都属于成分替换法。但CS方法对相关性要求高,需要利用直方图匹配将PAN波段处理成与MS的空间结构分量有相同的方差和均值。若预处理中出现错误配准,锐化结果也会出现光谱畸变。为改善上述问题,许多研究者提出了新的统计建模方法,准确仿真出全色图像和多光谱图像之间的关系,比如波段相关空间细节方法(band-dependent spatial detail, BDSD)[10]、自适应GS法[11]以及部分置换自适应CS法(partial replacement adaptive CS, PRACS)[12]。
MRA是先将图像分解到不同分辨率上,选取合适的锐化规则,对不同频率的频带系数进行处理,最后对调整后的系数采用多分辨率分析法逆变换得到锐化图像[13]。常用的MRA方法有:加性小波亮度比[14]、引导滤波器法[15]等。
基于模型的方法主要包括统计估计法、稀疏表征法和变分法。该类方法通过建立MS、PAN与锐化图像之间的观测模型,整个锐化过程描述为严格约束的线性函数。该类方法可以通过调整模型来减少光谱损失,但锐化过程中过于依赖先验条件或者合理假设。若先验条件不合理,将会导致锐化图像质量严重退化。
传统遥感图像锐化算法大多建立在线性模型之上,但多光谱图像的多波段与全色图像的单波段之间往往并非完全线性相关,而是存在复杂的光谱混叠现象。深度学习[16]凭借非线性、深度特征学习的能力,很好地解决了线性模型的缺陷。近年来,深度学习已被广泛运用于遥感图像锐化领域。目前,卷积神经网络(convolutional neural network,CNN)利用其非线性的映射,使锐化图像相较于待锐化图像有了明显的提升[17]。Zhong等[18]提出一种结合超分辨率的SRCNN模型和GS变换的图像锐化方法,该方法虽然有良好锐化效果,但处于传统图像锐化算法的框架下,且映射过程并非端到端。为实现端到端的映射,Masi等[19]依托超分辨率的方法提出一种名为PNN的网络,通过网络训练可直接得到全色图像和多光谱图像的相互关系。Rao等[20]提出一种基于残差卷积神经网络的锐化方法,该网络直接利用输入与输出的残差进行训练,缺点是3层浅层网络难以学习到深层的特征,易发生欠拟合。Wei等[21]提出将残差引入到锐化过程的网络DRPNN。Yang[22]提出PanNet,利用输入的全色图像和多光谱图像的细节信息预测高分辨率多光谱图像的细节,再利用预测出的多光谱图像的细节替换掉原来多光谱图像的细节,得到最终的锐化图像。Liu[23]提出利用双流网络进行遥感图像锐化,该方法采用2个分支提取全色图像与多光谱图像的图像特征,随后通过残差网络将特征输入到网络中,由于分支结构之间的独立性,使锐化结果更多地保留高光谱分辨率图像的光谱信息和高空间分辨率图像的空间信息。但目前的网络由于网络层数较浅,无法提取到待锐化图像的深层特征,网络各层之间相互信息利用不充分,会导致锐化结果出现一定的空间和光谱信息丢失。
针对上述问题,本文提出一种多重残差网络(multiple residual pan-sharpening neural network, MRPNN)方法。该方法基于深度卷积网络利用加深网络提取图像深层特征的特点,通过堆叠多个深度残差模块提取图像深层的空间和光谱特征,同时利用残差建立子块与子块之间的跳跃连接,从而把梯度信息传递到更深的网络层,避免梯度爆炸的问题,使网络更加高效。
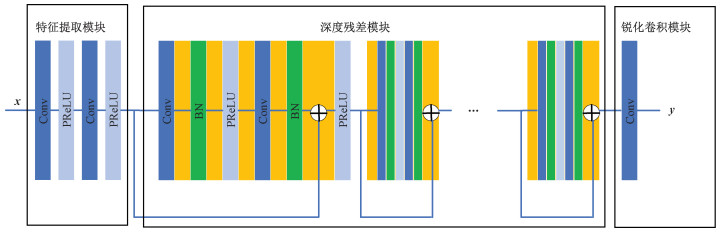
1 多重残差网络模型本文提出的MRPNN网络结构如图 1所示。下面将围绕网络结构的细节进行描述。
|
Download:
|
| 图 1 多重残差网络结构 Fig. 1 MRPNN structure | |
在深度学习中,若网络深度过深,会在反向传播过程中出现梯度消失或梯度爆炸现象,同时过深的网络由于缺乏约束,会导致网络性能下降[24]。在训练过程中引入残差模块,它利用恒等分支,使后向传播过程中梯度不需要经过那么多层,从而解决梯度消失或爆炸的问题。残差模块可表示为
| $ P(x)=F(x)+x . $ | (1) |
其中:F(x)是输入与输出之间的差,即为残差;x是残差网络的输入;P(x)是残差网络的输出。没有添加跳跃连接的原始网络学习的特征是P(x),而残差网络学习的特征是残差数据F(x)=P(x)+x,由于残差一般比较小,这使得残差网络学习的内容是稀疏的,因此无论是学习能力还是学习效率都大大提升,也使得网络更加容易收敛。
多光谱图像锐化过程可以从数学逻辑上表示为
| $ \boldsymbol{M}_i=\widetilde{\boldsymbol{M}}_i+k_i . $ | (2) |
其中:i表示多光谱图像对应的波段数,
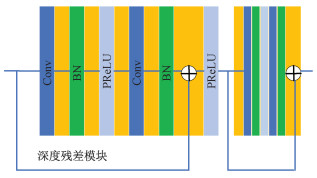
由图 1可知,MRPNN网络模型利用多个深度残差子模块进行堆叠。每个深度残差子模块由5层构成(见图 2),分别为卷积层、归一化层(batch normalization,BN)、带参数的修正线性单元(parametric rectified linear unit, PReLU)层、卷积层和归一化层。由多个子模块组成的深度残差块第n层的输出可以表示为
| $ x_n=\max \left(0, w_n \times x_{n-1}\right)+b_n, \quad n=1, 2, 3, \cdots . $ | (3) |
|
Download:
|
| 图 2 深度残差模块 Fig. 2 Depth residual module | |
其中:ωn是第n层的权重,xn-1是第n-1层的输出,bn是第n层的调整参数。
1.3 多重残差网络结构MRPNN网络由特征提取模块、深度残差模块、锐化卷积模块3个部分组成。特征提取模块采用2层卷积层进行特征提取,卷积核大小为9×9。深度残差模块采用的卷积核大小为3×3。最后用一个9×9的卷积核完成图像锐化。在深度残差模块中,每一次对子模块的调用都涉及局部残差的计算,多个子模块的堆叠起到深度卷积提取遥感图像深层特征的作用,在尽可能提高锐化图像的空间分辨率和光谱分辨率的同时,促进网络的收敛,避免了因网络层数增加而导致的梯度消失或爆炸现象。
深度学习训练的本质是寻找最佳网络参数的过程,而损失函数的存在能够约束网络训练的结果,即让网络训练的结果与网络标签相靠近。本文采用的损失函数为均方误差,公式如下
| $ \text { Loss }=\frac{1}{n} \sum\limits_{i=1}^n\left(y-f\left(x_1, x_2\right)\right)^2 . $ | (4) |
其中:x1,x2分别表示输入网络的全色图像与上采样多光谱图像;f(x1, x2)表示网络预测的锐化结果,即网络输出值;y表示原始多光谱图像对应的理想的高空间分辨率和高光谱分辨率锐化图像,也就是标签;n表示训练的图像个数。均方误差损失函数表示标签与网络输出值之间的差距。通过损失函数Loss的约束,使网络训练结果不断地接近于理想标签。
本文整个运算过程采用反向传播BP算法与随机梯度下降法[25]来学习。BP算法利用链式法则高效计算网络参数的偏导数并推算出损失函数Loss的梯度值,促进参数的优化。随机梯度下降法是沿着梯度方向求解最小值,即在对应点的反方向随机选取一部分样本,以不变的步长进行迭代搜索,以找寻损失函数的局部最小值。
2 实验与分析 2.1 实验设置 2.1.1 数据集实验数据为Worldview-2卫星获取的全色图像与多光谱图像,涵盖多种复杂的地物类型,例如城区、农田、郊区、水体等。全色图像的空间分辨率为0.4 m,多光谱图像共有8个波段,依次为蓝、绿、红、近红外、黄、海岸、红外、近红外,空间分辨率为1.6 m,2种类型遥感图像的空间分辨率之比为4。
由于没有真实的高空间分辨率多光谱图像作为标签,本文依据Wald协议[26]制作数据集并进行实验。制作数据集的流程为:预处理、采样、裁剪。
1) 在预处理部分,首先借助ENVI完成全色图像与多光谱图像的几何校正和图像配准,如果待锐化图像之间存在偏差,在后续的锐化过程中该误差会导致最终的锐化结果出现严重的信息失真。随后对配准完成的待锐化图像进行滤波,尽可能消除遥感图像受外部环境等噪声干扰造成的影响。滤波方式为中值滤波,它能有效地滤除脉冲噪声,较好地保留边缘信息。
2) 对数据集的采样按照Wald协议在MATLAB中进行,即用双三次插值法对全色图像进行4倍下采样,获得低分辨率的全色图像作为网络输入;用双三次插值法对多光谱图像先进行4倍下采样,再以同样的插值法进行4倍上采样,获得与全色图像同样尺寸的低分辨率多光谱图像作为网络输入,而原始多光谱图像作为网络标签。具体采样流程如图 3所示。

|
Download:
|
| 图 3 数据集采样流程图 Fig. 3 Data set sampling flow chart | |
3) 裁剪的具体步骤为:①用ENVI软件对完成预处理的多光谱图像与全色图像进行裁剪,裁剪后的全色图像尺寸为16 000×16 000×1,多光谱图像尺寸为4 000×4 000×8。在裁剪过程中严格要求全色图像与多光谱图像之间像素点位置相互匹配,根据比例严格对齐,以免对后续锐化实验结果造成影响;②利用python将上述初步裁剪完成的图像裁剪成32×32的图像集,每次裁剪相距16个像素点,完成裁剪后每类图像共计65 025张。最后以8∶2的比例随机分成训练集和测试集,这些数据主要为模型训练使用。
在模型训练完成后,为验证本文方法的性能,基于Worldview-2数据进行模拟数据和真实数据的测试实验。因为没有理想的高空间分辨率和高光谱分辨率图像作为参考图像,我们先进行模拟实验。模拟实验数据的制作过程与上面的训练数据制作过程一样,只是图像大小为200×200。但算法最终要在实际遥感数据上运用,所以又对真实遥感数据进行测试实验,直接将原始多光谱图像上采样后和原始全色图像作为待锐化图像输入网络,测试图像大小均为800×800。
2.1.2 训练参数设计训练数据集中低分辨率的全色图像、多光谱图像与理想的网络标签多光谱图像都裁剪成32×32大小,最终得到的训练数据总计有52 015对。实验迭代了200个周期,网络训练的批量输入大小设置为32,学习率为0.003。
实验所进行的训练在Linux发行版本Ubuntu 16.04系统中的Pytorch深度学习框架下实现,程序使用的语言为Python,训练过程采用GeForce RTX 3090显卡进行加速。
2.2 实验结果与分析为验证所提方法的锐化性能,将本文方法与几种传统的图像锐化方法和当前流行的深度学习图像锐化方法相比较。传统的方法有GS、高通滤波法(HPF)、BDSD、Brovery变换法和PRACS。基于深度学习的方法有PNN和DRPNN。
采用主观视觉评价和客观定量评价2种标准对锐化质量进行评价。对于模拟实验,主观视觉评价研究的是锐化结果与参考标签图像之间的光谱与空间信息之间的相似程度,相似程度越高,锐化效果越好。在客观定量评价方面,采用5种客观定量评价指标,分别为整体质量评价指标(universal image quality index,UIQI)、空间相关系数(spatial correlation coefficient,SCC)、全局相对光谱损失(error relative globale adimensionnelle de synthèse,ERGAS)、光谱角映射(spectral angle mapper,SAM)和全局融合质量评价指标(Q2n),从空间域和光谱域综合评价锐化结果。在真实实验中,由于没有理想的参考图像作为参照,直接将锐化图像与待锐化的多光谱图像以及全色图像相比较。若锐化结果与上采样的多光谱图像的光谱信息越接近,则锐化方法在光谱保真度上越好;若锐化结果与全色图像的空间信息越接近,则锐化方法在空间信息改善方面越好。同样,由于不存在理想的参考图像,客观定量评价采用3个不需要参考的评价指标来衡量锐化结果的质量,分别为无参考评价指标(quality with no reference,QNR)以及表征空间信息失真度的Ds和表征光谱失真度的Dλ。每个实验的评价结果均为所有测试图像评价结果的平均值。
2.2.1 模拟实验图 4展示了不同方法的模拟实验结果,包括5种传统的锐化算法、2种基于深度学习的锐化算法(PNN、DRPNN)以及本文提出的MRPNN算法。模拟实验对应的评价结果如表 1所示。

|
Download:
|
| 图 4 模拟实验的锐化结果图 Fig. 4 Pan-sharpening result diagram of simulation experiment | |
|
|
表 1 模拟实验客观定量评价结果 Table 1 Objective quantitative evaluation results of simulation experiment |
主观视觉评价方面,可以发现不管是对于传统的锐化算法,还是3种基于深度学习的锐化算法,都能实现在多光谱图像模糊的基础上提升其空间分辨率的目的。
将各种方法的锐化结果与参考图像(图 4(c))逐一对比,可以清晰地看出传统方法普遍存在一定程度的光谱失真。其中Brovey方法出现了严重的光谱失真,该方法在空间分辨率上有一定的提高,但锐化结果整体偏蓝,与原始的参考图像存在较大的偏差。观察锐化实验结果,发现在各方法锐化结果图中普遍存在一些小范围的光谱失真现象,例如图 4(c)参考图像中用红色方框标出位置的红色小车,各方法在此位置都变成了小白点。原因可能是本文的训练数据集是根据Wald协议制作的,涉及对原始多光谱图像进行降采样处理,而降采样后的多光谱图像在红色小车位置的红色光谱已经出现光谱信息丢失。以此降采样后的多光谱图像和全色图像作为待锐化图像,将导致锐化结果在红色小车位置出现光谱失真而显示小白点。此外,相较于传统算法,基于深度学习的锐化算法具有更好的锐化效果。这类方法利用非线性模型学习到更多的全色图像的空间细节,并将空间细节注入到输入的多光谱图像中,极大程度地提高了多光谱图像的空间分辨率。从全局看,基于深度学习的锐化结果都具有良好的光谱保真度,锐化效果优于绝大部分传统方法。对于图 4中山体绿化部分,PNN和DRPNN法出现了明显的沟壑,而MRPNN法在这部分与参考图像更加接近,也更加平滑,表明相较于PNN和DRPNN方法,MRPNN法在空间细节保留上更强。
由表 1可知,基于深度学习的遥感图像锐化算法的质量评价指标在整体上要优于传统方法的结果,其中MRPNN的各项指标在所有方法里都是最佳的。以整体质量评价指标UIQI为例,MRPNN方法的UIQI指标为0.938 2,DRPNN、PNN的值分别为0.896 5、0.888 1,而在传统算法里表现较好的是HPF方法,其指标为0.871 4。在空间分辨率的提升上,SCC指标可以衡量锐化结果与参考图像之间的空间相关性,MRPNN方法的SCC值为0.969 1,DRPNN、PNN的SCC值分别为0.912 2、0.923 9,而传统方法里最优的HPF方法,其SCC指标为0.899 2。此外本文方法的ERGAS、SAM、SCC、UIQI、Q2n相较于DRPNN方法分别提高24.4%、26.7%、6.2%、4.7%、6.3%,表明相较于所对比的深度学习方法,本文方法能够学习到更深层次的图像特征,从而更好地保留图像的空间与光谱信息。
2.2.2 真实实验图 5展示了5种传统锐化算法、2种基于深度学习的锐化算法(PNN、DRPNN)以及本文提出的MRPNN的真实实验的锐化结果,其对应的定量评价结果如表 2所示。

|
Download:
|
| 图 5 Beijing Academy of Food Sciences Fig. 5 Pan-sharpening results of real experiments | |
|
|
表 2 真实实验客观定量评价结果 Table 2 Objective quantitative evaluation results of real experiments |
在主观视觉评价方面,将各类方法的实验结果与输入的全色图像进行对比,可以看出,各类方法整体上锐化结果在空间细节上都得到了提升,且本文方法锐化结果相比于其他结果拥有更丰富的空间细节。将锐化结果与多光谱图像进行对比,可以看出传统的方法存在严重的光谱畸变、光谱失真现象,例如BDSD方法、Brovery方法都出现了明显的伪影现象。而深度学习算法有着更好的非线性表达能力,保留了更多的光谱信息。
由表 2的结果可知,MRPNN法在所有实验方法中取得了最佳的QNR值,这表明MRPNN法在空间分辨率提升和光谱分辨率信息保持上都有着出色的表现。遥感图像的锐化对象是复杂多变的,而基于深度学习的锐化算法利用非线性特征表达能力,使其对多样复杂环境的锐化性能呈现出稳定性。从表 2也可发现,PRACS方法比深度学习锐化算法表现好,特别是其空间信息质量是所有方法里面最好的,这是由于该方法通过将多光谱图像中的空间强度置换为全色图像,保留了全部的空间信息,所以使其具有与原始全色图像更接近的空间分辨率。而在模拟实验部分,该方法表现较差。但本文方法是利用深度卷积网络以及残差网络的特性,综合性地对全色图像和多光谱图像进行锐化,能够在空间特征和光谱信息保留二者之间取得较好的平衡。虽然本文方法未在Ds取得最好的实验结果,但整体而言取得了最佳的QNR值,且该方法不管在真实实验还是模拟实验中都取得了较好的实验结果。
综合模拟实验和真实实验的结果,可以看出本文提出的锐化方法相较于经典深度学习锐化算法PNN、DRPNN的锐化性能有着明显的提高。
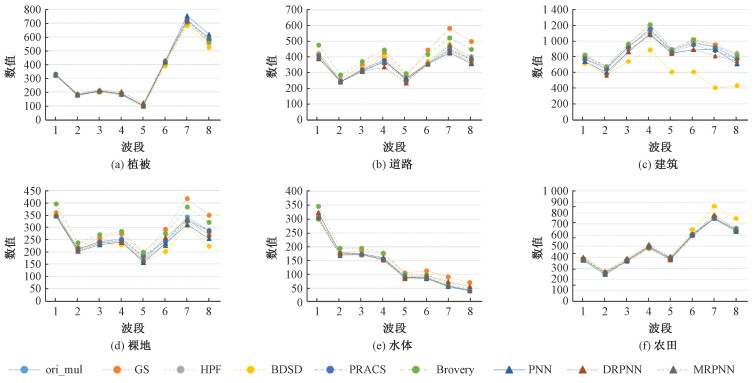
2.2.3 光谱曲线评价光谱曲线评价是评价多光谱图像锐化质量的一个重要指标。本文选取研究区中有代表性的地物进行光谱曲线评价。研究区内主要地物(水体、道路、建筑、裸地、水体、农田)的光谱曲线如图 6所示。通过比较锐化图像和原始多光谱图像的光谱曲线形状以及光谱曲线的数值差异来评价锐化图像的光谱质量。
|
Download:
|
| 图 6 各研究区主要地物的光谱曲线 Fig. 6 The spectral curve of main ground objects in each study area | |
从图 6可以看出,本文方法在各种地物中的光谱曲线(黑色)与原始多光谱图像的光谱曲线(蓝色)十分接近,每个波段的数值与多光谱图像的相差很小,说明本文方法的锐化结果保留了原始多光谱图像的光谱特性。相比于其他7种方法, 本文方法更接近于多光谱图像的光谱曲线,说明该方法具有较好的光谱保真度。
2.2.4 消融实验为验证本文模型设计的有效性,又进行了消融实验。使用WorldView-2卫星数据集,以MRPNN方法为基础架构,通过改变深度残差模块(如图 2所示)的比例来测试本文方法的可靠性。改变深度残差模块的比例是在一个利用残差模块搭建的网络中,在原有残差模块的数量上,保留残差模块一定比例数量的过程。本文方法的原始框架是对20个深度残差模块进行堆叠,在消融实验中通过分别保留80%、50%、20%和0个残差模块验证该模块的有效性。
图 7展示了不同比例残差模块的实验结果。

|
Download:
|
| 图 7 消融实验的锐化结果图 Fig. 7 Pan-sharpening results of ablation experiments | |
从图中可以看出,没有深度残差模块的锐化结果(图 7(c))存在明显的斑点现象,而有深度残差模块的锐化结果(图 7(d)~7(f))都较为平滑,具有较高的空间分辨率。这说明MRPNN方法能够有效地提升图像锐化的效果。此外,随着残差模块比例的增加,锐化结果的空间分辨率和光谱分辨率也有显著提高,尤其是在残差模块比例较低时,锐化结果出现明显的光谱失真,图中有零散的小红点区域。因此,从主观视觉评价的角度来看,本文模型中的深度残差模块对遥感图像锐化具有明显提升作用。
根据表 3的数据,可以分析出深度残差模块的比例对图像锐化的影响。从表中可以看出,随着深度残差模块的比例增加,锐化图像的光谱分辨率和空间分辨率都有显著的提高。同时,客观评价指标也显示有残差模块的模型在ERGAS、SAM、SCC和UIQI等方面都优于没有残差模块的模型。这些结果证明本文提出的深度残差模型对图像锐化存在有效的优化作用。
|
|
表 3 消融实验客观定量评价结果 Table 3 Objective quantitative evaluation results of ablation experiment |
本文提出一种基于多重残差网络的多光谱图像锐化方法MRPNN。该方法类似于DRPNN方法,不同之处在于该方法是利用残差技术改进深度卷积网络中浅层特征的利用度,提取深度的空间和光谱特征。将PNN方法、DRPNN方法这2种经典深度学习方法作为对比方法,分析与讨论本文所提方法。
由于本文使用WorldView-2卫星数据进行训练,因此计算模型参数量与所需计算力都采用尺寸为32×32× 9的训练集。3种深度学习的模型参数量与所需计算力如表 4所示。
|
|
表 4 3种深度学习的模型参数量与所需计算力 Table 4 Three types of deep learning model parameters and required computational power |
从表 4可以看出,MRPNN模型参数量与所需计算力介于PNN方法与DRPNN方法之间。MRPNN网络模型比DRPNN方法深,但参数量与所需计算力比DRPNN方法小,原因是该方法通过堆叠多个深度残差模块提取深度的空间和光谱特征,同时利用残差建立子块与子块之间的跳跃连接。因此,可知通过构建残差网络模块堆叠的形式,能够在减小所需计算力的同时,提高锐化图像的空间分辨率与光谱分辨率。
3 结论针对当前传统多光谱图像锐化方法存在光谱失真,现有的基于深度学习的多光谱图像锐化方法存在网络层间信息利用不充分、网络层数较浅等问题,提出一种基于多重残差网络的多光谱图像锐化方法MRPNN。在CNN与残差网络的基础上,利用多层残差结构对图像深层的空间和光谱特征进行提取。多层残差网络的引入,既解决了训练过程中梯度消失或爆炸的问题,又加速了网络的收敛速度。经过主观视觉评价和客观定量评价,与5种传统方法和2种深度学习锐化算法的真实实验和模拟实验的对比结果表明,MRPNN比常用的锐化方法明显地提高了锐化图像的精度,改善了锐化图像的质量,保留了待锐化图像中重要的空间与光谱信息。但是,本文实验目前所采用的数据集单一,只采用了Worldview-2卫星遥感数据,未来会在其他卫星数据上进行泛化性研究,探究本文方法对不同类型多光谱数据的锐化能力。最后,对于本文方法在模拟实验部分以降采样的多光谱图像作为待锐化图像而出现局部光谱信息丢失的问题,未来将进行以原始待锐化图像为参考的算法研究。
| [1] |
孙洪泉, 窦闻, 易文斌. 遥感图像融合的研究现状、困境及发展趋势探讨[J]. 遥感信息, 2011, 26(1): 104-108. Doi:10.3969/j.issn.1000-3177.2011.01.021 |
| [2] |
Dadrass Javan F, Samadzadegan F, Mehravar S, et al. A review of image fusion techniques for pan-sharpening of high-resolution satellite imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 171: 101-117. Doi:10.1016/j.isprsjprs.2020.11.001 |
| [3] |
王华伟. 基于IHS变换的多光谱和全色图像融合算法研究[D]. 成都: 西南交通大学, 2016.
|
| [4] |
Ranchin T, Wald L. Fusion of high spatial and spectral resolution images: the ARSIS concept and its implementation[J]. Photogrammetric Engineering and Remote Sensing, 2000, 66: 49-61. |
| [5] |
Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. Doi:10.1109/TSP.2006.881199 |
| [6] |
Nasr A, Darwis A, Shaheen S. Use of intensity-hue-saturation (IHS) transformations in change detection of multitemporal remotely sensed data[C]//Conference on Image and Signal Processing for Remote Sensing Ⅶ, Sep 18-21, 2001, Toulouse, France. 2001. DOI: 10.1117/12.454166.
|
| [7] |
Laben C A, Brower B V. Process for enhancing the spatial resolution of multispectral imagery using pan-sharpening: US6011875[P]. 2000-01-04.
|
| [8] |
Tu T M, Su S C, Shyu H C, et al. A new look at IHS-like image fusion methods[J]. Information Fusion, 2001, 2(3): 177-186. Doi:10.1016/S1566-2535(01)00036-7 |
| [9] |
Abdolahpoor A, Kabiri P. New texture-based pansharpening method using wavelet packet transform and PCA[J]. International Journal of Wavelets, Multiresolution and Information Processing, 2020, 18(4): 2050025. Doi:10.1142/s0219691320500253 |
| [10] |
Vivone G. Robust band-dependent spatial-detail approaches for panchromatic sharpening[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 6421-6433. Doi:10.1109/TGRS.2019.2906073 |
| [11] |
Aiazzi B, Baronti S, Selva M. Improving component substitution pansharpening through multivariate regression of MS+Pan data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10): 3230-3239. Doi:10.1109/TGRS.2007.901007 |
| [12] |
Choi J, Yu K, Kim Y. A new adaptive component-substitution-based satellite image fusion by using partial replacement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 295-309. Doi:10.1109/TGRS.2010.2051674 |
| [13] |
Vivone G, Alparone L, Chanussot J, et al. A critical comparison among pansharpening algorithms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2565-2586. Doi:10.1109/TGRS.2014.2361734 |
| [14] |
Kaplan N H, Erer I. Bilateral filtering-based enhanced pansharpening of multispectral satellite images[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(11): 1941-1945. Doi:10.1109/LGRS.2014.2314389 |
| [15] |
Liu J M, Liang S L. Pan-sharpening using a guided filter[J]. International Journal of Remote Sensing, 2016, 37(8): 1777-1800. Doi:10.1080/01431161.2016.1163749 |
| [16] |
Fang F M, Li F, Shen C M, et al. A variational approach for pan-sharpening[J]. IEEE Transactions on Image Processing, 2013, 22(7): 2822-2834. Doi:10.1109/TIP.2013.2258355 |
| [17] |
Azarang A, Ghassemian H. A new pansharpening method using multi resolution analysis framework and deep neural networks[C]//The 3rd International Conference on Pattern Recognition and Image Analysis (IPRIA). April 19-20, 2017, Shahrekord, Iran. IEEE, 2017: 1-6. DOI: 10.1109/PRIA.2017.7983017.
|
| [18] |
Zhong J Y, Yang B, Huang G Y, et al. Remote sensing image fusion with convolutional neural network[J]. Sensing and Imaging, 2016, 17(1): 10. Doi:10.1007/s11220-016-0135-6 |
| [19] |
Masi G, Cozzolino D, Verdoliva L, et al. Pansharpening by convolutional neural networks[J]. Remote Sensing, 2016, 8(7): 594. Doi:10.3390/rs8070594 |
| [20] |
Rao Y Z, He L, Zhu J W. A residual convolutional neural network for pan-shaprening[C]//2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP). May 18-21, 2017, Shanghai, China. IEEE, 2017: 1-4. DOI: 10.1109/RSIP.2017.7958807.
|
| [21] |
Wei Y C, Yuan Q Q, Shen H F, et al. Boosting the accuracy of multispectral image pansharpening by learning a deep residual network[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1795-1799. Doi:10.1109/LGRS.2017.2736020 |
| [22] |
Yang J F, Fu X Y, Hu Y W, et al. PanNet: a deep network architecture for pan-sharpening[C]//2017 IEEE International Conference on Computer Vision (ICCV). October 22-29, 2017, Venice, Italy. IEEE, 2017: 1753-1761. DOI: 10.1109/ICCV.2017.193.
|
| [23] |
Liu X Y, Wang Y H, Liu Q J. Remote sensing image fusion based on two-stream fusion network[C]//International Conference on Multimedia Modeling. Cham: Springer, 2018: 428-439.10.1007/978-3-319-73603-7_35.
|
| [24] |
He K M, Sun J. Convolutional neural networks at constrained time cost[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). June 7-12, 2015, Boston, MA, USA. IEEE, 2015: 5353-5360. DOI: 10.1109/CVPR.2015.7299173.
|
| [25] |
Stephan M, Hoffman Matthew D, Blei David M. Stochastic gradient descent as approximate Bayesian inference[J]. Journal of Machine Learning Research, 2017, 18: 4873-4907. |
| [26] |
Wald L, Ranchin T, Mangolini M. Fusion of satellite images of different spatial resolutions: assessing the quality of resulting images[J]. Photogrammetric Engineering and Remote Sensing, 1997, 63(6): 691-699. |
 2025, Vol. 42
2025, Vol. 42 


