2. 中国科学院大学电子电气与通信工程学院, 北京 100049;
3. 北京市遥感信息研究所, 北京 100192
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Institute of Remote Sensing Information, Beijing 100192, China
星载合成孔径雷达(synthetic aperture radar, SAR)具有空间分辨率高、覆盖范围广的特性,有多种工作模式,在不同领域被广泛应用,是遥感信息获取的重要工具之一[1-2]。在星载SAR系统中,精确的卫星轨道数据对于SAR成像处理至关重要。卫星轨道误差会造成雷达平台和场景之间的距离历程计算错误,最终导致成像质量恶化,出现分辨率下降、目标散焦、信噪比降低等问题[3-4]。
虽然新一代全球导航卫星系统(global navigation satellite system,GNSS)的定位精度不断提高,但所能提供的cm级的信息仍然很难满足某些高分辨率或超高分辨率SAR系统的要求。而且高精度的运动传感器配置需要高额的成本和较重的载荷,在实际应用中有诸多不便。比如对于造价成本较低的商用小卫星而言,出于成本等因素的考虑,装配的定位系统精度往往会与要求的高分辨率不匹配。此外,实际中还存在一些无法高效、准确获取轨道信息的特殊情形,如SAR实时成像中定轨精度可能只有m级程度[5],而精确的轨道星历需要几小时甚至几天的地面处理之后才能获取;意外情况下还会导致卫星导航数据缺失等。在这些情况下,轨道误差会成为高分辨率成像的主要限制因素[6]。因此需要研究通过数据处理的方式修正轨道误差进而得到良好聚焦图像的方法。
在机载SAR数据处理中,自聚焦算法可以根据原始的SAR数据估计出相位误差并进行补偿。作为应用最广泛的自聚焦算法,相位梯度自聚焦(phase gradient autofocus, PGA)算法[7-10]是一种适用于各种形式相位误差估计问题的非参数化算法。但在实际应用中,尤其对于无明显特征点的场景,PGA经常不能达到良好的聚焦效果。另一类常用的自聚焦算法是基于度量的算法,它们以图像的聚焦指标为标准进行最佳相位误差参数的搜索,如图像熵[11-13]、锐度[4, 14-15]和对比度[16-18]等。与PGA相比,基于度量的自聚焦算法在图像信噪比较低且场景中没有明显散射点的情况下仍然有效,但由于它们只能对参数模型描述的相位误差进行估计,因此使用场景有限。另外,文献[19-20]中都涉及基于自聚焦估计得到的相位误差反推机载SAR航迹的三维运动误差。在这些方法中,相位误差与平台三维运动误差之间的对应根据距离历程与二者分别的映射关系实现。对每个方位采样时刻,利用估计出的三维运动误差对原始航迹数据进行校正,再在成像后实现机载SAR图像空变误差的补偿。
星载轨道与机载SAR航迹相比,具有良好的平滑特性。因此,若在自聚焦过程中充分利用该轨道特征,预计可以大幅度提高星载SAR自聚焦的鲁棒性、处理效率及聚焦效果。考虑到星载SAR轨道为平滑的曲线,对于1景星载SAR数据,其轨道在地固坐标系下的三维坐标可以利用3个低阶(如4阶)多项式函数来近似表达。对于精度较低的实时GPS轨道数据,这种低阶多项式的轨道表达方式还可以滤除其中的高频误差。基于这种低阶多项式轨道描述模型,本文通过估计轨道多项式的各个系数来估计和补偿误差轨道信息引入的斜距误差,实现星载SAR图像的自聚焦。但是,由于轨道多项式中各阶系数的数量级差别很大,直接估计各个系数实施较为困难。而多项式的系数往往可以通过几个已知的轨道位置进行拟合得出。于是,本文选取若干个不同方位采样时刻下的轨道点(4阶多项式时需要选取5个点),通过对这些点位置的调整等效实现对多项式参数的估计,从而显著提高了估计算法实现的便利性。同时,本文方法采用对比度作为衡量图像聚焦程度的评价指标,通过调整各个轨道点位置直到获得最优对比度。
本文所提出的自聚焦方法主要包含2个处理阶段。第1阶段,选取位于整幅图像不同区域的几幅小图像切片(如四角区域各选择1个切片),对各个切片以成像结果对比度最优为准则搜索最优的预设轨道点位置,同时得到该切片的聚焦图像。第2阶段,对切片轨道估计结果进行融合,得到适用于整景图像的轨道估计结果。由于此轨道可以对第1阶段所选小图像切片达到最优的聚焦效果,如果切片的位置及数量选取得当(如场景四角),可以认为该轨道估计结果能够实现对整幅图像的良好聚焦。
本文所提出的方法具有以下优点:第一,利用卫星轨道的平滑特性,通过3个低阶多项式表达卫星轨道,将自聚焦问题转化为轨道多项式的系数估计问题,降低了估计难度,从而提高了估计鲁棒性;第二,将多项式系数的估计问题转换为几个轨道点位置的搜索问题,提高了搜索算法实现的便利性;第三,由于每个图像切片非常小,再加上如下所述的特殊成像方法以及GPU(graphics processing unit)的辅助,大大减少了第1阶段各个待评估轨道下成像处理的计算量及运算时间;第四,第2阶段的最终轨道估计不涉及成像处理,因此可以更加精确而快速地搜索到适用于整景的轨道估计结果。
需要进行说明的是:1)本文提出的自聚焦方法适用于SAR不同工作模式;2)由于方法的第1阶段以图像质量作为优化指标,因而无法准确估计误差中的线性项与常数项,第2阶段以距离历程误差为优化标准时也需要相应去除线性项及常数项的影响,所得到的最终轨道估计结果中线性项及常数项也需要去除;3)方法选在垂直轨道平面内调整预设轨道点位置寻求最优轨道拟合,可以降低所选轨道点的搜索维度,相应地,其得到的轨道估计主要针对在垂直轨道平面内的误差,未考虑沿航向的轨道误差,沿航向误差可通过速度估计等其他方法进行估计;4)估计轨道不一定会收敛至与真实情况相符,但轨道多项式基于使得各切片良好聚焦的最优距离历程,最终能够确保整景SAR图像的自聚焦。
1 基本原理 1.1 轨道多项式模型星载SAR卫星平台通常沿着一条平滑的曲线轨道航行。而在星载SAR系统中(高分辨率星载SAR通常在凝视聚束或滑动聚束模式下工作),一次成像时间通常不会超过1 min。因此,对于1景星载SAR数据,其合成孔径时间内的卫星轨道三维坐标与方位时间η之间的关系可用低阶多项式进行描述,如下
| $ \left\{\begin{array}{l} X_S=a_0+a_1 \eta+a_2 \eta^2+a_3 \eta^3+a_4 \eta^4, \\ Y_S=b_0+b_1 \eta+b_2 \eta^2+b_3 \eta^3+b_4 \eta^4, \\ Z_S=c_0+c_1 \eta+c_2 \eta^2+c_3 \eta^3+c_4 \eta^4 . \end{array}\right. $ | (1) |
其中:(XS, YS, ZS)为瞬时卫星位置坐标;ai, bi, ci, i=0, …, 4, 表示三维方向的多项式系数,它们可以借助已知的轨道位置数据进行多项式拟合或利用轨道六根数信息计算得出。
这种用多项式模型描述星载SAR轨道的方法能够准确表达短时间内具有良好平滑特性的轨道数据,不但表达方式简洁,而且可以滤除离散的实时轨道数据(如1 Hz的实时GPS数据)中的高频误差。更重要的是,通过多项式的轨道表达,可以将SAR图像自聚焦问题转化为轨道多项式系数的估计。通过对轨道多项式系数的优化,可以得到使整幅SAR图像良好聚焦的轨道估计。
1.2 图像聚焦的最大对比度方法基于最大对比度原理的自聚焦[16-18]是一种常用的基于度量的自聚焦方法。它在应用过程中对成像算法没有限制,以SAR图像的最大对比度为优化准则调整相位误差模型的参数,对比度最大时,则认为结果图像达到最优的聚焦质量。
对于一幅实图像g(i, j),其中i=1, 2, …, M, j=1, 2, …, N, 其对比度可以定义为
| $ C=\frac{1}{M N} \sum\limits_{i=1}^M \sum\limits_{j=1}^N\left[g^2(i, j)-\frac{1}{M N} \sum\limits_{i=1}^M \sum\limits_{j=1}^N g^2(i, j)\right]^2 . $ | (2) |
实际经验表明,对几乎各种场景,最大对比度法都是一种非常可靠的聚焦度量手段,对比度达到最大时,SAR图像的聚焦效果也能够同时达到最优。因此本文借助最大对比度法作为监测手段搜索最优轨道多项式系数。
2 基于小图像切片的轨道估计 2.1 针对小图像切片的轨道估计如前文所述,对于某一选定的小图像切片,能够使其良好聚焦的轨道多项式系数估计可以等效为若干个轨道点在垂直轨道的平面内的位置估计。当用式(1)中的4阶多项式描述轨道时,轨道多项式估计可以等效为5个轨道点在垂直轨道平面内的位置搜索,使小图像切片的聚焦质量达到最优,即对比度达到最大。最后由最优的5个轨道点位置在3个维度上分别拟合4阶多项式,即得到最优的多项式轨道估计结果。而对于单个切片来说,合成孔径时间相对较短,尤其对于一般分辨率的SAR系统,可能只有几秒。因此,为减少运算量,可以使用更低阶数(如2阶)的多项式表达轨道,对应的等效轨道点可降为3个。
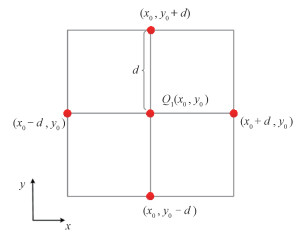
本文方法基于上述思路,提出一种轨道点位置搜索策略。以2阶多项式的情况为例进行说明:对某一小图像切片,在整景数据的轨道范围内选取起点Q1、中间点Q2、终点Q3 3个时刻的轨道位置,以此等效轨道在三维空间内的2阶多项式表达。对每个等效轨道点,以其初始位置为中心,并以步长d在垂直轨道平面内设置5个点为待评估的轨道点位置。以点Q1为例,假设垂直轨道平面的2个坐标轴为x、y轴,待评估的5个点位置如图 1所示。则在预设3个等效轨道点的情况下,共产生5×5×5=125种轨道点位置组合,即对应125个待评估的轨道点。
|
Download:
|
| 图 1 轨道点Q1处待评估的5个点位置 Fig. 1 The five points to be evaluated at orbit point Q1 | |
在上述轨道点待评估位置的设置中,对每个预设轨道点选择图 1中的5个位置作为待选点而不是3×3点阵中全部9个位置,是为了减少产生的轨道点位置组合数,从而大幅降低搜索中需要利用所有可能的拟合轨道进行成像处理的计算量,提高收敛速度。同时,保留的5个点位置可以使轨道点的二维坐标在搜索平面上沿各自的方向不断优化。
利用每种轨道点位置组合多项式拟合后得到的待评估轨道,对回波数据进行成像处理,并用1.2节中的图像对比度方法得到每个待评估轨道对应的图像对比度,选取其中最大的对比度值,其对应的轨道点位置即为当前的轨道估计结果。
为实现精确的自聚焦,往往还需要对轨道点位置进行迭代搜索,不断优化估计的轨道位置对图像的聚焦质量改善程度。于是,在经过一轮搜索得到当前最优轨道估计结果之后,根据此时的估计状态修改步长,并更新轨道点初始位置:若估计结果与原位置相比有所变动,且变动后轨道与原轨道相比呈非常数或非线性变化,说明估计结果为有效的优化,将轨道点初始位置更新为当前的估计结果,展开新一轮的搜索,寻求具有更大聚焦图像对比度的轨道点位置;如果当前轨道与原轨道相比仅有线性分量的差别,则认为在当前步长条件下,不会再有新的有效优化,进而将步长减半,用修正后的步长重新调整轨道点的位置。直到步长d足够小时,即迭代得到的聚焦图像对比度改善非常小时(如小于0.01),结束估计并以此时的估计结果作为最终的轨道点位置。根据最终的轨道点位置在3个维度上分别拟合多项式,即为该图像最终的多项式轨道估计结果。
在上述搜索轨道点位置的过程中,步长d的初始值通常根据轨道的误差程度设置,将初始步长设置为与轨道误差大致相当的数值,再根据迭代的估计状态减半或保持,从而可以较快较好地收敛到最优结果。本方法的搜索策略同样适用于更高阶次多项式的轨道估计,但计算量将增大。比如,4阶多项式的情况下,需要5个等效轨道点,相应待评估轨道将由125个增至5×5×5×5×5=3 125个。
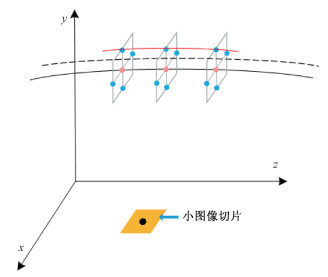
小图像切片的一次卫星轨道搜索过程如图 2所示。假设SAR卫星平台沿z方向移动,实线表示从卫星定位系统获得的不准确的轨道位置,虚线是卫星平台的实际航行轨道。实线上的点表示用来执行轨道多项式参数搜索的初始预设的轨道点,对每个轨道点按上述方法在垂直轨道平面设置5个待评估的轨道点位置如图中所示。红色曲线则为搜索过程中的一条待评估的卫星轨道。根据上述处理步骤迭代搜索,最终得到针对小图像切片的轨道多项式系数估计。
|
Download:
|
| 图 2 小图像切片的一次卫星轨道搜索过程 Fig. 2 The searching process of the satellite orbit for one patch | |
根据2.1节介绍的基于等效轨道点调整的轨道优化估计方法,其中需要对成像场景中的一个小图像切片利用不同的轨道进行多次成像处理(例如对于2阶多项式情况,迭代次数为P,则需要进行125×P次成像处理),并用最大对比度法衡量每次处理结果的聚焦程度。为了能够尽快收敛到最优结果,除尽可能缩小切片尺寸之外,还需要设法减小每次成像处理的运算量。我们采用文献[21]提出的方法,简化上述重复成像处理的步骤:先在距离压缩后的SAR数据中,截取小图像切片所对应的数据范围(方位向向两侧延伸1个合成孔径,距离向向远距延伸距离弯曲量);然后对截取数据在二维频域用基于初始轨道对切片中心构建的二维匹配滤波器进行匹配滤波,得到初步聚焦的散焦小图像切片。根据文献[21],该二维匹配滤波器为
| $ \begin{gathered} H\left(f_\tau, f_\eta\right)=\sqrt{\frac{\mathrm{d} f_\eta}{\mathrm{d} \eta}} \cdot \exp \left[\mathrm{j} 2 \mathsf{π}\left(\eta-\eta_c\right) f_\eta\right] \cdot \\ \left.\exp \left\{\mathrm{j} \frac{4 \mathsf{π}\left(f_0+f_\tau\right)}{c} \cdot\left[R(\eta)-R_c\right]\right\}\right|_{\eta=f^{-1}\left(f_\eta\right)}, \end{gathered} $ | (3) |
其中:fτ,fη分别为距离及方位频率;f0为发射信号载频;c为光速;R(η)为切片中心位置对应的距离历程,Rc为R(η)的最小值。η为由下式(驻定相位原理)确定的与方位频率fη对应的方位时刻
| $ f_\eta=f(\eta)=-\frac{2\left(f_0+f_\tau\right)}{c}\left[\frac{\mathrm{~d} R(\eta)}{\mathrm{d} \eta}\right] . $ | (4) |
对匹配滤波后的数据返回二维时域后,得到初步聚焦的图像。此时,可将该图像按照图像切片的位置及大小进行裁切,得到只进行了初步二维匹配滤波(未进行其他空变处理)的小图像切片。基于该初步聚焦的小图像切片,在对2.1节方法中生成的不同轨道进行评估时,可在二维频域应用待评估轨道构建式(3)所示的匹配滤波器,同时抵消掉初始轨道的匹配滤波效果,实现成像参数的快速更新,进而在二维时域得到新轨道下的聚焦切片图像。
| $ H_1\left(f_\tau, f_\eta\right)=\left.H\left(f_\tau, f_\eta\right)\right|_{\substack{\text { new } \\ \text { orbit }}}-\left.H\left(f_\tau, f_\eta\right)\right|_{\substack{\text { initial } \\ \text { orbit }}} . $ | (5) |
根据待评估轨道更新匹配滤波器的公式如式(5)所示。由于该步匹配滤波的数据量与原切片图像相同,因此运算量很小,适合进行多次重复运算。另外,对于分辨率较高的SAR系统,或切片较大以至于需要考虑切片内的空变性时,可以在应用匹配滤波器H1(fτ, fη)之后继续应用文献[21]提出的基于重采样的切片内空变补偿方法,即对应用H1(fτ, fη)之后的二维频谱分别在距离向及方位向按照下列公式进行重采样
| $ f_\tau=\frac{\left(f_0+f_\tau^{\prime}\right)\left[R_{B c}-R_{A c}\right]-\frac{c}{2}\left[\eta_B-\eta_A\right] \cdot f_\eta}{R_B\left(\eta_B\right)-R_A\left(\eta_A\right)}-f_0, $ | (6) |
其中:f′τ为重采样后的新距离频率;RA(ηA)与RB(ηB)为切片的位于方位中心线上最近距及最远距2点的距离历程,其最小值分别为RAc与RBc,与当前方位频率fη根据式(4)对应的方位时刻分别为ηA与ηB。
| $ f_\eta=\frac{\eta_{B c}-\eta_{A c}}{\eta_B-\eta_A} f_\eta^{\prime}-\frac{2\left(f_0+f_\tau\right)}{c} \cdot \frac{R_B\left(\eta_B\right)-R_A\left(\eta_A\right)}{\eta_B-\eta_A}, $ | (7) |
其中:f′ η为重采样后的新方位频率;RA(ηA)与RB(ηB)为切片位于距离中心线上两端的2点之间的距离历程,其零多普勒时刻分别为ηAc与ηBc,与当前方位频率fη根据式(4)对应的方位时刻分别为ηA与ηB。
2.3 由切片轨道估计结果构建整景轨道用上述处理方法可以实现针对小图像切片估计轨道多项式系数,使当前图像切片良好聚焦。然而由于小区域的图像切片对轨道三维特性非常不敏感,并且切片所估计的轨道结果不能实现对常数及线性误差的精确估计与补偿。因此,对于一个小图像切片,会存在多个使其良好聚焦的轨道,按上述方法估计的结果不一定会收敛到实际的天线平台轨道,无法达成整个场景各处的良好聚焦。
虽然如此,但对于一个能使得小图像切片良好聚焦的轨道估计结果,由其对切片中心点所构建的距离历程除去可能存在误差的常数及线性项后是与实际相符的可靠信息。因此,本文方法第2阶段利用在整幅场景不同区域选取的小图像切片所得到的轨道估计信息,提取其对切片中心点的距离历程并除去常数及线性项,用于估计能使整景各处聚焦效果改善的轨道。
整景轨道估计首先需要能够保证所有小切片的良好聚焦,再借助合适的切片选取,进而满足全场景的聚焦。因此方法第2阶段的优化目标为,通过在垂直轨道平面内重新调整新的预设轨道点位置,使得待评估轨道下各切片中心的距离历程与第1阶段估计结果所对应距离历程相比整体误差最小,从而实现各切片估计结果的融合,得到适用于整景图像的最优轨道估计。其中,由于需要去除距离历程信息中的常数与线性项,方法中使用距离历程差值的2次微分消除相应的影响,并将所有结果平方后累加,用于评估轨道的效果。假设在整景图像区域中选取了N个小图像切片,对每个小图像切片,在切片中心点的合成孔径范围内的M个时刻(M等于切片轨道估计多项式阶数加1),计算上述整体误差值,即对于第p个待评估轨道
| $ E(p)=\sum\limits_{n=1}^N \sum\limits_{m=1}^M\left(\frac{\mathrm{~d}^2 r_{n, m}(\eta)}{\mathrm{d} \eta^2}\right)^2, $ | (8) |
其中:η为方位时间,rn, m(η)表示第n个切片在第m个时刻的2种距离历程的差值。
综上,对于1景SAR图像,构建整景轨道的实现步骤如下:
1) 在整景图像区域中选取N(N≥4)个小图像切片,并用2.1节中的方法对切片进行轨道多项式系数估计。为了提供充分的轨道三维变化信息,所选择的切片位置应尽可能在场景内分散分布(如场景四角)。此外,选择更多的切片将有助于提高估计的鲁棒性及估计精度。一般推荐选择4个以上的切片以保证估计的精度,若选取更少的切片得到的结果相对效果不佳,且对切片包含的轨道信息要求更高。在实际应用中,考虑到照射场景的复杂多样性,最好选择成像内容比较丰富(避免水体等无任何纹理区域)的区域,以提高单个切片中心点距离历程的估计精度。此时可能需要进行人工选取及确认。
2) 以4阶多项式的整景轨道为例,其等效为5个轨道点的位置组合。一般选择整景轨道自始至终范围内等间隔的5个时刻的轨道点。
3) 以每个轨道点为中心,在垂直轨道的平面内设置间距为D的B×B二维点阵。点阵中的每个点的位置均为原轨道点的待评估位置。此时,可以构造P=(B×B)5种待评估轨道。相对于2.1节中的搜索,由于此阶段只需进行数值运算而不涉及成像处理,因此较多的待搜索轨道数量不会导致巨大的计算耗时。B的取值一般为3或5,以能够准确和快速地收敛至最终的搜索结果。
4) 在每种轨道情况下,对每个小图像切片,在切片中心点根据式(8)计算E(p)。
5) 从P个待评估轨道的误差度量值E(p)中选取最小值,并将其对应的5个轨道点位置作为当前的估计结果。
6) 根据当前的估计状态进行如下后续处理:
① 若5个轨道点的估计结果与原位置相比有所变动,且变动后轨道与原轨道相比呈非常数或线性变化,则将轨道点初始位置更新为当前的估计结果,重复步骤3)~6),寻求具有更小轨道误差度量的轨道点位置,否则缩减步长D为D/2;
② 若步长D足够小,即P种轨道的误差度量E(p)差异非常小(如小于1×10-7),则结束估计,并以此次估计结果作为最终的轨道点位置,否则以新的步长重复步骤3)~6),寻求具有更小轨道误差度量的轨道点位置;
7) 将5个轨道点的估计结果在3个维度上分别拟合4阶多项式。
8) 调整轨道多项式系数的常数及线性项,使得其与原始轨道的误差在最小二乘意义上最小,并以调整后的轨道多项式系数所描述的轨道作为适用于所有小图像切片的最终整景轨道估计结果。
由于所选择的小图像切片分散在整景图像的不同区域,且根据上述方法所得到的最终整景轨道估计结果能够使得各个切片良好聚焦,因此我们预期整景图像此时都能得到良好聚焦。实际经验表明,选择整景四角位置的4个小图像切片(或者再加场景中少量切片),按照上述方法处理之后,所估计得到的最终轨道一般都能够使得整景图像都良好聚焦。另外,在实际应用中,所选的场景切片可能会具有不同的高程,此时在有外源数字高程模型(digital elevation model,DEM)数据可资利用的情况下,每个切片的成像处理可以根据外源DEM提供的高程信息进行成像处理,以排除场景高程变化的影响。
3 实验结果及分析为验证上述方法的有效性,本节选用一块高分3号星载SAR的滑动聚束模式数据,其相关参数如表 1所示,首先利用该组参数设计点目标实验对算法进行验证,之后将方法用于该实际数据的处理。
|
|
表 1 系统参数 Table 1 System parameters |
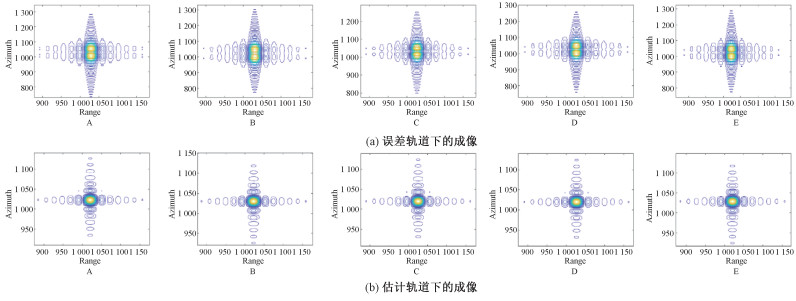
点目标实验中采用了一段真实SAR轨道数据,并设置了大小为24 000×24 000个像素点的观测场景,在场景的四角和中心各放置一个点目标。为方便描述,它们分别记为场景四角点目标A、B、D、E和中心点目标C。接下来,通过在三维方向上对原轨道多项式各阶系数进行微调,得到加入误差的轨道。利用加入误差的轨道根据2.2节中的方法对点目标进行成像处理,5个点目标均在方位向出现了明显的散焦,如图 3(a)所示。
|
Download:
|
| 图 3 点目标成像 Fig. 3 Imaging results of the point targets | |
对场景四角的4个点目标A、B、D、E,截取以点目标为中心的4 096×4 096个像素点组成的小切片。基于得到的这4个小图像切片,先根据2.1节的方法采用2阶轨道多项式模型分别估计使切片对比度最大的轨道。再根据2.3节的方法,利用上一阶段的结果得到对各切片中心点的距离历程信息,基于4阶多项式模型对整景轨道进行估计。两阶段的搜索步长均设置为0.4 m,第1阶段基于切片的估计经过5次迭代,第2阶段整景轨道估计经过6次迭代,最终得到能够同时改善这4个点目标聚焦效果的轨道多项式。利用得到的轨道进行成像,改善的点目标成像结果如图 3(b)所示。特别注意图 3(b)中利用估计的轨道,对没有选作切片参与估计过程的点目标C的成像结果,可以看到点目标C的成像质量也得到了良好改善。利用本方法进行轨道估计处理前后5个点目标的峰值旁瓣比(peak sidelobe level ratio, PSLR)与积分旁瓣比(integrated side lobe ratio, ISLR)具体数值如表 2所示。可见,利用估计轨道成像所得图像的聚焦效果较之前有了十分显著的改善。
|
|
表 2 点目标在方位向的性能指标结果 Table 2 Performance of the point targets in the azimuth direction |
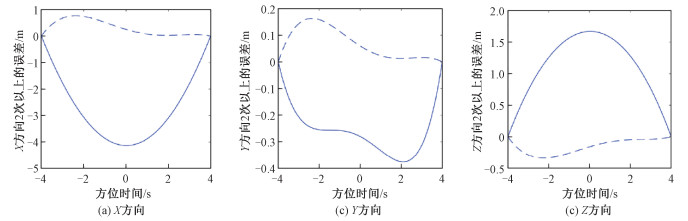
我们利用实际数据对本文提出的轨道估计方法进行了验证。图 4为该数据对应的一幅整景SAR图像(一级图像,横向为距离向)。由于缺少原本散焦的实际图像数据,本文通过在X、Y、Z方向加入如图 5中实线所示的误差(除去常数及线性项后)对方法的有效性进行验证。从整景图像中选取6个小图像切片,各切片位置如图 4中6个实线框所示,切片(多视前大小)为1 024像素×1 024像素。各切片的散焦图像如图 6所示。对每个切片利用2.1节所提出的方法进行轨道多项式系数估计,得到的聚焦结果图像如图 7所示,由成像结果可见,每个切片都得到了理想的聚焦,而且与原(未加入误差前)切片图像相比,补偿后的切片图像的目视聚焦效果仍稍有改善,可见原轨道仍有少量误差存在。

|
Download:
|
| 图 4 整景SAR图像 Fig. 4 SAR image of the whole scene | |
|
Download:
|
| 图 5 三维轨道误差(2阶及以上的分量) Fig. 5 Orbit errors in three directions | |

|
Download:
|
| 图 6 切片的散焦成像结果 Fig. 6 Defocused image of the selected patches | |

|
Download:
|
| 图 7 用估计轨道成像得到改善后的切片图像 Fig. 7 Imaging results of the patches using the estimated orbit | |
然后根据6个切片的轨道估计结果按照2.3节的方法构建整景轨道,得到的轨道与原始轨道的误差如图 5中虚线所示。可见,与加入误差后的轨道相比,2次及以上的轨道误差大大减小。而由于方法是基于多个切片的聚焦质量搜索得到的距离历程信息,并且原轨道也可能存在误差,此时得到的轨迹估计可能仍与真实轨迹有差异,因而依然存在少量2次及以上的轨道误差。再根据整景图像的聚焦效果对估计轨道进行评估。选取如图 8(a)的场景(图 4中部虚线方框)中心点一个切片(大小为512像素×512像素),利用构建的整景轨道进行成像处理,结果如图 8(b)所示。可见,该切片也能够良好聚焦。由此可以证明根据本文方法估计得到的轨道,能够有效地改善图像模糊,提高成像质量,实现SAR图像的自聚焦。

|
Download:
|
| 图 8 整景图像虚线区域改善前后的成像结果 Fig. 8 Imaging results of the dotted patch before and after the orbit estimation | |
图 9给出了对散焦整景SAR图像分别利用PGA算法与本文所提方法处理后截取的局部区域图像以及细节放大图,可以看出图像的聚焦效果均有一定程度的改善。而对比图 9(b)和9(c)可以看出,PGA算法对图像该区域的改善效果不如本文所提方法,图像中仍然存在较严重的方位向的散焦现象,相比之下,经过本文方法处理后图像内场景内容变得清晰,整体聚焦性能较好。表 3展示了整景SAR图像在不同处理情况下图像质量指标的变化,可以看出,利用本文方法得到的重聚焦图像相对于PGA在熵和对比度指标方面都取得了较优的性能。这是因为PGA算法基于相位误差沿距离向具有冗余性的假设,将同一距离单元的相位误差看作是相同的,因此对大场景情况下的相位误差在距离向的空变特性无能为力。本文所提方法则通过对整景轨道的搜索估计,最终能够实现大幅星载SAR图像的全场景聚焦,得到全局质量改善的图像。同时所提方法简单易行,适用于不同工作模式下获取的SAR数据。

|
Download:
|
| 图 9 不同处理情况下的局部图像及细节图 Fig. 9 Local and detail image after different processing | |
|
|
表 3 整景图像的评价指标变化情况 Table 3 Evaluation parameters of the whole scene image |
在算法运算速度方面,实验中算法在一台NVIDIA C2075 GPU上运行,每个切片基于2阶轨道模型的估计耗时约为30 s,基于4阶轨道模型的整景轨道构建耗时约为25 s。可见,本文提出的方法具有较为理想的运行效率。
4 结论本文针对星载SAR的自聚焦问题提出一种基于低阶多项式轨道估计与对比度最优聚焦质量评估的解决方法。算法中考虑了星载SAR轨道的平滑特性,利用三维空间中的低阶多项式对卫星轨道进行描述,将自聚焦问题转化为几个多项式系数的估计问题。进一步考虑到各阶多项式系数的量级差异,又将轨道多项式系数的估计问题转化为几个轨道点的位置估计,即通过调整几个轨道点在垂直轨道平面上的位置等效实现轨道多项式参数的估计。方法简单易行,以图像切片的最大化对比度法进行轨道估计,并融合得到使整幅图像聚焦质量改善的卫星轨道多项式,以消除大场景中的空变误差影响,为星载SAR的快速、精确处理提供了新思路,具有较强的适用性和通用性。在实际应用中,利用GPU的高性能处理能力,可以进一步提高算法的运算效率。仿真和实际数据实验表明,通过合适的小切片选取,利用所得到的整景轨道能够获得场景各处的良好聚焦图像。
| [1] |
李春升, 于泽, 陈杰. 高分辨率星载SAR成像与图像质量提升方法综述[J]. 雷达学报, 2019, 8(6): 717-731. Doi:10.12000/JR19085 |
| [2] |
Meng D D, Ding C B, Hu D H, et al. On the processing of very high resolution spaceborne SAR data: a chirp-modulated back projection approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 191-201. Doi:10.1109/TGRS.2017.2744649 |
| [3] |
Fornaro G. Trajectory deviations in airborne SAR: analysis and compensation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 997-1009. Doi:10.1109/7.784069 |
| [4] |
Gao Y, Yu W D, Liu Y B, et al. Sharpness-based autofocusing for stripmap SAR using an adaptive-order polynomial model[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(6): 1086-1090. Doi:10.1109/LGRS.2013.2286410 |
| [5] |
Yu Z J, You Z. Real-time onboard orbit determination using GPS navigation solutions[C]//2011 First International Conference on Instrumentation, Measurement, Computer, Communication and Control. October 21-23, 2011, Beijing, China. IEEE, 2012: 949-952. DOI: 10.1109/IMCCC.2011.239.
|
| [6] |
Muff D G, Blake A P, Horne A M. Spaceborne SAR autofocus[C]//IEE Colloquium on Recent Developments in Radar and Sonar Imaging Systems: What Next?. December 12-12, 1995, London, UK. London: IET, 2002: 11/1-1111. DOI: 10.1049/ic:19951576.
|
| [7] |
Wahl D E, Eichel P H, Ghiglia D C, et al. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827-835. Doi:10.1109/7.303752 |
| [8] |
Chan H L, Yeo T S. Noniterative quality phase-gradient autofocus (QPGA) algorithm for spotlight SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1531-1539. Doi:10.1109/36.718857 |
| [9] |
Ye W, Yeo T S, Bao Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2487-2494. Doi:10.1109/36.789644 |
| [10] |
Evers A, Jackson J A. A generalized phase gradient autofocus algorithm[J]. IEEE Transactions on Computational Imaging, 2019, 5(4): 606-619. Doi:10.1109/TCI.2019.2899453 |
| [11] |
Xi L, Guosui L, Ni J L. Autofocusing of ISAR images based on entropy minimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1240-1252. Doi:10.1109/7.805442 |
| [12] |
Wang J, Liu X. SAR minimum-entropy autofocus using an adaptive-order polynomial model[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 512-516. Doi:10.1109/LGRS.2006.878446 |
| [13] |
Yang L, Xing M, Zhang L, et al. Entropy-based motion error correction for high-resolution spotlight SAR imagery[J]. IET Radar, Sonar & Navigation, 2012, 6(7): 627-637. Doi:10.1049/iet-rsn.2011.0078 |
| [14] |
Fienup J R. Synthetic-aperture radar autofocus by maximizing sharpness[J]. Optics Letters, 2000, 25(4): 221-223. Doi:10.1364/OL.25.000221 |
| [15] |
Fienup J R, Miller J J. Aberration correction by maximizing generalized sharpness metrics[J]. Journal of the Optical Society of America. A, Optics, Image Science, and Vision, 2003, 20(4): 609-620. Doi:10.1364/josaa.20.000609 |
| [16] |
Berizzi F, Dalle Mese E, Martorella M. Performance analysis of a contrast-based ISAR autofocusing algorithm[C]//Proceedings of the 2002 IEEE Radar Conference (IEEE Cat. No. 02CH37322). April 25-25, 2002, Long Beach, CA, USA. IEEE, 2002: 200-205. DOI: 10.1109/NRC.2002.999719.
|
| [17] |
Berizzi F, Martorella M, Cacciamano A, et al. A contrast-based algorithm for synthetic range-profile motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3053-3062. Doi:10.1109/TGRS.2008.2002576 |
| [18] |
Berizzi F, Corsini G. Autofocusing of inverse synthetic aperture radar images using contrast optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(3): 1185-1191. Doi:10.1109/7.532282 |
| [19] |
Ran L, Liu Z, Zhang L, et al. An autofocus algorithm for estimating residual trajectory deviations in synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3408-3425. Doi:10.1109/TGRS.2017.2670785 |
| [20] |
Liang Y, Li G F, Wen J, et al. A fast time-domain SAR imaging and corresponding autofocus method based on hybrid coordinate system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8627-8640. Doi:10.1109/TGRS.2019.2921917 |
| [21] |
Meng D D, Huang L J, Qiu X L, et al. A novel approach to processing very-high-resolution spaceborne SAR data with severe spatial dependence[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 7472-7482. Doi:10.1109/JSTARS.2022.3202932 |
 2025, Vol. 42
2025, Vol. 42 


