海底管道为输送油气的主要介质,保证其在工作运行期间的安全性是能否顺利进行海洋油气开发的关键。人类海洋活动的激增,使得部分管道铺设区与船舶作业区发生重叠,船舶抛锚平台作业等第三方活动难免发生坠锚事故,对管道造成撞击损伤,引起环境污染及经济损失。为避免第三方活动对管道的破坏,有必要对其进行可靠性及风险分析。目前,国内外研究人员对于管道风险分析的研究做了一些工作,获得了一些有价值的理论及实验成果。DNV提出了一种管道受坠物撞击作用下的风险分析方法[1];M Zeinoddini提出了管线在侧向点荷载作用下的变形和破坏模式[2];英国能源部基于吊机意外事故的统计资料给出了典型下落荷载的概率及各类物体的起吊坠落概率[3];郭鸿雁基于事故树理论,对第三方活动致使管道失效的各种原因进行了分析[4];刘学涛给出了不同锚泊作业情况下管道受撞击作用下的概率计算模型[5];丁红岩改进了DNV规范推荐方法中关于管道碰撞概率的计算方法,并对海底管道进行了风险分析[6]。
对于海底管道风险分析,以前的分析方法大多是基于DNV规范推荐方法(以下称DNV法)。该方法首先将坠物划分不同的类别,再分别计算每类坠物的失效概率,分两步进行:第一步计算坠物对管道的撞击概率Phit;第二步计算管道在给定撞击能量下的失效概率Pf。则总失效概率Pf, total为上述两步所得结果的乘积。在第二步计算中,DNV法对每一类坠物的撞击能量划分固定的范围,并赋予各范围相应的概率值,以此值及相关规定来计算失效概率Pf。该算法难以考虑坠物质量、尺寸对失效概率的影响:对于类别虽相同,但质量、尺寸等皆存在差异的船锚,其具有不同的撞击能量,但DNV法对其赋予固定的撞击能量及概率,使求得的失效概率与真实的失效概率值之间存在偏差,影响管道的设计与防护工作。
针对上述问题,基于可靠度理论,在DNV法的基础上,对第二步算法进行改进,给出了一种管道失效概率的计算方法:首先按DNV法中第一步的算法计算管道的撞击概率;随后建立管道的极限状态方程并求解,将所求结果替代DNV法第二步中所赋予的各能量范围的概率值,并以此结果及相关规定计算失效概率;最后将上述步骤的结果相乘即得到总失效概率。该方法可考虑船锚质量、尺寸及管道尺寸、材料强度等因素的影响,避免了上述误差的出现。
本文首先介绍了管道失效概率的计算方法与步骤。随后结合工程实例对管道失效概率的影响因素进行了分析,同时进一步考虑随机变量的变异性,探讨了管道失效概率对各变量的敏感性。最后总结了分析结果,为管道的设计及防护提供技术参考。
1 风险分析方法管道风险分析的主要任务是求得管道的失效概率,在此基础上根据其失效概率及相应的风险接受准则即可对其进行风险分析。
1.1 管道失效概率计算管道失效概率的计算同DNV法类似,分两步进行:第一步计算船锚击中管道的概率Phit;第二步计算管道在给定撞击能量作用下的失效概率Pf,则管道总的失效概率为
| $ {P_{{\rm{f,total}}}} = {P_{{\rm{hit}}}} \cdot {P_{\rm{f}}} \cdot N \cdot {P_{\rm{d}}}。$ | (1) |
式中:N为海域每年经过船舶的数量; Pd为每艘船平均发生脱锚事故的概率。
1.1.1 管道撞击概率的计算管道的撞击概率按DNV法中第一步的算法进行计算:
(1) 选取最有可能发生坠锚事故的一点为圆心,并以一定步长(如10 m)递增的长度为半径绘制同心圆。
(2) 计算船锚坠落在各圆环内的概率:船锚在海水中的漂移服从正态分布,如式(2)所示:
| $ p\left( x \right) = \frac{1}{{\sqrt {2\pi \delta } }}{e^{ - \frac{1}{2}\left( {\frac{x}{\delta }} \right)2}}。$ | (2) |
式中:p(x)为距坠落点垂线x时触底的概率;x为船锚触底点距坠落点垂线的距离(m);δ为侧向偏移量(m)。
则船锚击中每个圆环的概率如式(3)所示:
| $ \left\{ \begin{array}{l} {P_{{\rm{hit, }}}}_i({r_0}\left( {i - 1} \right) \le x \le {r_0}i) = \\ \int_{_{ - {r_0}i}}^{^{{r_0}i}} {p\left( x \right){\rm{d}}x - \int_{ - {r_0}(i - 1)}^{^{{r_0}(i - 1)}} {p\left( x \right){\rm{d}}x{\rm{ }}\,\,\,\,i = 2, 3, \ldots , n} } \\ {P_{{\rm{hit, 1}}}}(x \le {r_0}) = \int_{_{ - {r_0}}}^{^{{r_0}}} {p\left( x \right){\rm{d}}x} {\rm{ }}\,\,\,\,i = 1 \end{array} \right\}。$ | (3) |
式中:Phit, i为船锚坠落在第i个圆环内的概率;n为圆环个数。
(3) 计算船锚撞击每段圆环内管道的概率:求出管道落在每段圆环内的长度Lsl, i(i=1, 2, …, n),则船锚撞击圆环内管道的概率按式(4)计算:
| $ {P_{{\rm{hit, sl}}, i}} = \frac{{{p_{{\rm{hit}}, i}}}}{{{A_{{\rm{r}}, i}}}}\cdot{L_{{\rm{st}}, i}}\cdot(D + B)。$ | (4) |
式中:D为管道外径(m);B为物体宽度(m),一般取12 m;Ar, i为第i个圆环的面积(m2)。
(4) 计算船锚对整个管道的撞击概率:
| $ {P_{{\rm{hit}}}} = \sum\limits_{i = 1}^n {{P_{{\rm{hit}}, {\rm{sl}}, }}_i} 。$ | (5) |
式中,Phit为锚船锚对整个管道的撞击概率。
1.1.2 管道在给定撞击能量下的失效概率该部分的计算采用本文给出的方法进行,即基于可靠度理论求出管道在给定条件(撞击能量、管道材料、船锚尺寸等)的失效概率Pf。
(1) 撞击能量DNV规范[2]中指出坠物在下沉过程中当重力与浮力达到平衡时,最终会保持匀速下降,由此可得船锚的速度为:
| $ {v_c} = \sqrt {2m\left( {1 - \frac{{{\rho _{\rm{w}}}}}{{{\rho _{\rm{s}}}}}} \right)\frac{g}{{{C_{\rm{D}}}{\rho _{\rm{w}}}A}}} 。$ | (6) |
式中:m为锚的重量(kg);g为重力加速度(m/s2);ρw、ρs分别为水、锚的密度(kg/m3);CD为拖曳系数;A为挡水面积(m2)。
船锚最终的撞击能量由本身的动能以及附加水质量产生的动能两部分组成,其表达式为:
| $ E = \frac{1}{2}(m + {m_{\rm{a}}})v_{_1}^w = \frac{1}{2}m\left( {1 + {C_{\rm{a}}}\frac{{{\rho _{\rm{w}}}}}{{{\rho _{\rm{s}}}}}} \right)v_{_{\rm{c}}}^2。$ | (7) |
式中:ma为附加水质量(kg);Ca为附加质量系数。
(2) 管道变形深度DNV规范[2]中关于混凝土保护层吸收能量EK的公式可按式(8)或式(9)计算:
| $ {E_{\rm{K}}} = Y \cdot b \cdot h \cdot {x_0}。$ | (8) |
| $ {E_{\rm{K}}} = Y \cdot b\cdot\frac{4}{3}\sqrt {D \cdot x_0^3} 。$ | (9) |
式中:Y为混凝土压碎强度(MPa);h、b、x0为坠物的深度、宽度、嵌入混凝土的深度(m);D为管道外径(m)。
上述公式中管道变形量未包含在内,且嵌入深度x0通常需假设以进行混凝土层吸能的计算。故DNV规范法难以考虑混凝土保护层吸收能量值与管道变形之间的关系,无法反应真实的吸能值,使计算结果存在偏差。故本文按文献[7-8]中的方法计算管道变形深度,该方法可考虑上述关系。船锚作用在管道上的体积为:
| $ {A_{\rm{c}}} = \alpha \pi \left( {R_3^2 - R_2^2} \right)/2\pi 。$ | (10) |
| $ {A'}{{\rm{c}}}\left\{ \begin{array}{l} {\rm{ \mathsf{ π} }} \times ({\rm{ \mathsf{ π} }}/2 - \alpha )/2{\rm{ \mathsf{ π} }} \times \\ \left[ {{{\left( {{R_3} - {R_1}} \right)}^2} - {{\left( {{R_2} - {R_1}} \right)}^2}} \right]\,\,\,\,\,\alpha \ge {\rm{ \mathsf{ π} }}/4\\ {\rm{ \mathsf{ π} }} \times \left[ {{{\left( {{R_3} - {R_1}} \right)}^2} - {{\left( {{R_2} - {R_1}} \right)}^2}} \right]/8{\rm{ }}\,\,\,\,\,\,\,\alpha < {\rm{ \mathsf{ π} }}/4 \end{array} \right\}。$ | (11) |
式中:R1为管道半径(m);R2为包含防腐层厚度的半径(m),R2=R1+tcorr;R3为包含混凝土保护层厚度的半径(m),R3=R2+tcon;tcorr为管道防腐层厚度(m);tcon为管道混凝土层厚度(m);α=arccos[(R1-Hp, c)/R1]。
| $ V = 2({A_{\rm{c}}} + {A'}{{\rm{c}}})/d。$ | (12) |
式中:d为船锚作用在管道上的宽度(m),与锚形状有关。
则混凝土层及管道吸收的能量Ec、Es分别为:
| $ {E_{\rm{c}}} = V\cdot{f_{{\rm{cw}}}}。$ | (13) |
| $ {E_{\rm{s}}} = E\cdot{E_{\rm{c}}}。$ | (14) |
| $ {H_{{\rm{p, c}}}} = \left( {\frac{{{f_{\rm{n}}}\cdot{E_{\rm{s}}} \cdot D_{\rm{m}}^{^{1/2}}}}{{100\;{m_{\rm{p}}}}}} \right)。$ | (15) |
式中:fn为冲击能的耗散/吸收系数;fcw为混凝土破坏强度(MPa);mp为等效弹性动量(N),mp=σyt2/4;σy为管道屈服强度(MPa);Dm为管道平均直径(m),Dm=D-t;t为管道壁厚(m)。
由式(10)~(15)可知,管道变形量Hp, c与混凝土吸收能量Ec有关,而Ec又为Hp, c的函数,故Hp, c的计算需进行迭代求解,按如下步骤进行:1)赋予管道变形量迭代初值,令Hp, c, old=Hp, c, 0;2)将Hp, c, old代入式(10)~(15)计算,得到管道变形量的计算值Hp, c, new;3)判断|Hp, c, new-Hp, c, old|≤ε,若满足要求,则Hp, c=Hp, c, new,否则令Hp, c, old=Hp, c, new,转步骤(2)。
(3) 管道的极限状态方程影响管道可靠度的因素众多:管道因实际截面与设计截面的偏差使得管道尺寸发生变动;钢材的制造加工、混凝土的配合比、密度的变动使得管道材料存在变异性。故在本文可靠度分析中,将管道的外径D、壁厚t、屈服强度σy、混凝土破坏强度fcw作为随机变量处理,其统计特性见表 1[6]。
|
|
表 1 管道的统计特性 Table 1 Statistical properties of pipeline |
如表 2所示,DNV规范[2]中把管道的损伤分为3个等级:D1,未造成烃类泄露且不需要维修;D2,未造成烃类泄露,但需要维修;D3,造成烃类、水的泄露。对不同的损伤等级,管道变形深度有不同的规定,故可得管道变形深度的控制值为δlim, i=0.05·i·D(i=1, 2, 3, 4)。则管道的极限状态方程为:
| $ \begin{array}{l} {Z_i} = {g_i}(D, T, {\sigma _y}, {f_{{\rm{cw}}}}) = \\ {\rm{ }}{\delta _{{\rm{lim}}, i}} - {H_{{\rm{p, c}}}}(D, T, {\sigma _{\rm{y}}}, {f_{{\rm{cw}}}}) = 0(i = 1, 2, 3, 4)。\end{array} $ | (16) |
|
|
表 2 管道撞击承载能力及损坏程度级别表 Table 2 Impact capacity and damage classification of steel pipelines |
式中,Hp, c(·)为管道变形深度(m),D为管径(m)、t壁厚(m)、屈服强度σy(MPa)、混凝土破坏强度fcw(MPa)的函数。
(4) 管道的可靠度求解由式(10)~(16)可知,其中管道的变形深度为上述随机变量的不明函数,其功能函数为隐式形式,JC法难以求解其可靠度。Monte-Carlo法、响应面法[9]等方法是求解隐式功能函数的常用方法,但前者需要大量的抽样及数值计算,很不经济。响应面法则是根据一系列确定性试验拟合一个响应面来模拟真实的极限状态曲面,从而采用一次二阶矩法进行可靠度计算,其兼顾计算效率与精度,故本文选用响应面法进行可靠度求解。
(5) 失效概率的确定根据式(16)可解得对应的可靠度指标βi′(i = 1, 2, 3, 4),按Pf=1-Φ(β)的对应关系可求出相应的失效概率P′f, i(i=1, 2, 3, 4)。
按式(17)可求得表 2中第1列所对应的失效概率:
| $ \left\{ \begin{array}{l} {{P''}_{{\rm{f, 1}}}} = {P'}({\delta _{{\rm{lim, }}i}}/{H_{{\rm{p, c}}}} < 0.05) = 1 - {P'}{ {{\rm{f, 1}}}}{\rm{, }}i = 1\\ {{P''}_{{\rm{f, 1}}}} = {P'}{{\rm{f}}}\{ 0.05\left( {i - 1} \right) < {\delta _{{\rm{lim, }}i}}/{H_{{\rm{p, c}}}} < 0.05i\} \\ \;\;\;\;\;\;\; = {{P'}_{{\rm{f}}, i - 1}} - {{P'}_{{\rm{f}}, i}}, \;\;i = 2, 3, 4\\ {{P''}_{{\rm{f, 5}}}} = {{P'}_{\rm{f}}}({\delta _{{\rm{lim}}, i}}/{H_{{\rm{p, c}}}} > 0.20) = {{P'}_{{\rm{f}}, 4}}{\rm{, }}i = 5 \end{array} \right\}。$ | (17) |
按式(17)计算表 2中每一行中不同损伤等级下的失效概率。
| $ {{P}_{\text{f}}}{{_{,}}_{{{D}_{i,j}}}}={{{{P}''}}_{\text{f},i}}\cdot {{D}_{i,j}}(i=1,2,\ldots ,5,j=2,3,4)。$ | (18) |
式中, Di, j表示第i行、第j列的条件概率系数。
DNV规范[2]中规定出现D2及以上等级的损伤为失效,则管道在给定撞击能量下的效概率为D2级、D3级失效概率之和,按式(19)计算。
| $ {P_{\rm{f}}} = \sum\limits_{i = 1}^5 {\sum\limits_{j = 2}^3 {{P_{\rm{f}}}{{_, }_{{D_{i, j}}}}。} } $ | (19) |
风险接受准则是规定时间内可接受的风险等级。DNV规范根据失效概率将其划分为5个等级(见表 3),据此可进行风险评估及制定减小风险的措施。
|
|
表 3 管道失效概率等级划分 Table 3 Annual failure frequency ranking for pipeline |
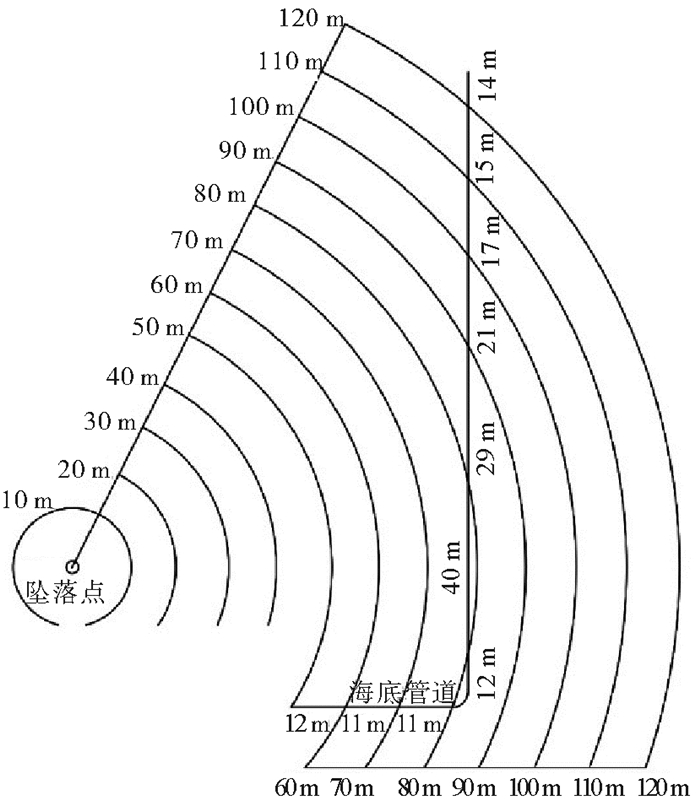
如图 1所示,以该工程为例,对海底管道在船锚撞击作用下的失效概率进行计算,并分析影响管道失效概率的因素及海底管道的受损失效风险:本文主要从船锚质量、管道尺寸及材料、管道所在区域距船锚坠落点距离这三个方面进行分析。同时考虑随机变量变异性,探讨了管道失效概率对影响其大小的各变量的敏感性。
|
图 1 管道场地规划图 Fig. 1 Field layout of submarine pipeline |
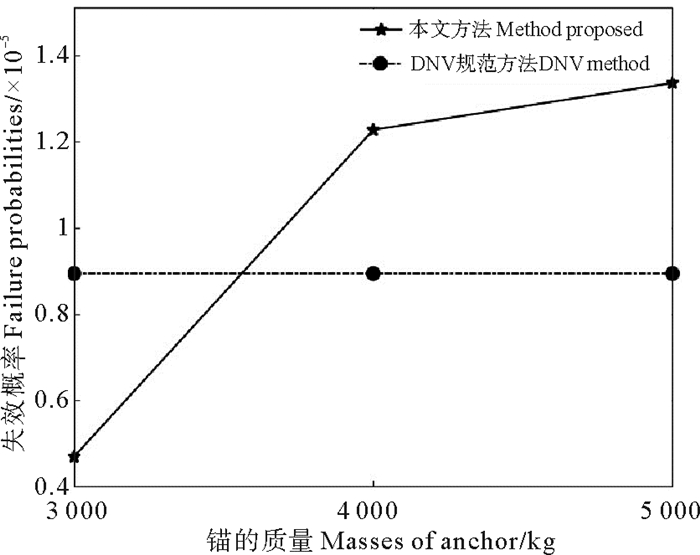
DNV法中,对于同一类别的坠物无法考虑质量对管道损伤的影响,而本文的方法则可予以考虑。对于表 4中的管道4,选取质量分别为3 000、4 000、5 000 kg的霍尔锚[10]作为坠物,使用DNV法及本文方法计算其失效概率,结果如图 2所示。由计算结果可知,本文方法可考虑质量变化的影响:失效概率随着船锚质量的增加而增大。由表 3可知,随着船锚质量的增加,该管道的风险等级由1级变为了2级,受损的风险增大。由此可见,对于质量不同的船锚,应采取不同的防护措施,以降低风险。而DNV法的结果为一常量,无法考虑质量变化的影响,会使结果偏于危险,与实际情况不符。
|
图 2 管道失效概率随船锚质量的变化 Fig. 2 Failure probabilities with different masses of anchor |
|
|
表 4 管道参数 Table 4 Parameters of pipelines |
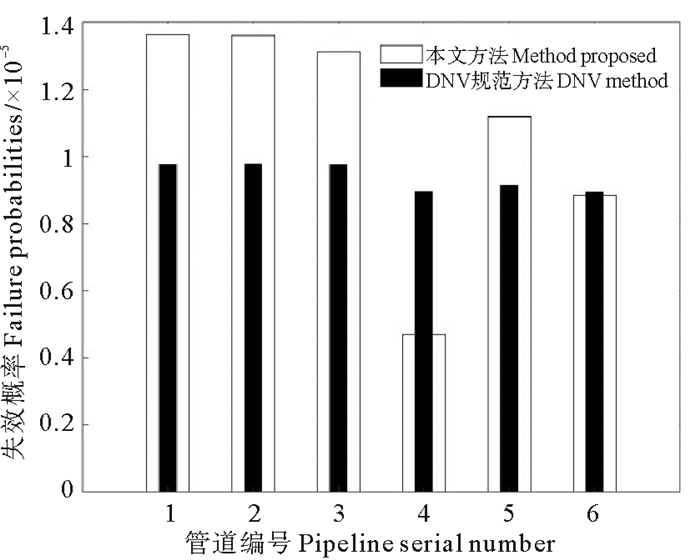
管道尺寸、材料影响管道对于撞击能量的吸收,从而对管道的失效概率产生影响。为分析其影响,选取表 4中6种不同管道,使用DNV法及本文方法进行管道的失效概率计算,其结果如图 3所示。由计算结果可知,对于本文方法,管道尺寸、材料对失效概率的影响较大:不同管道的失效概率皆不相同,对于管道4,其管径、壁厚较其他管道大,抵抗撞击的能量较强,其风险等级为1级,而其余管道抵抗撞击的能力较差,风险等级为2级;而对于DNV法,管道尺寸、材料失效概率的影响几乎无影响,失效概率基本保持为一常量,风险等级皆为1级。对于管道1、2、3、5,DNV法偏于危险,而对于管道4,DNV法则偏于保守。由以上分析可知,管道尺寸、材料对于失效概率有所影响。应予以考虑,以降低受损风险。
|
图 3 管道失效概率随不同管道的变化 Fig. 3 Failure probabilities with different pipelines |
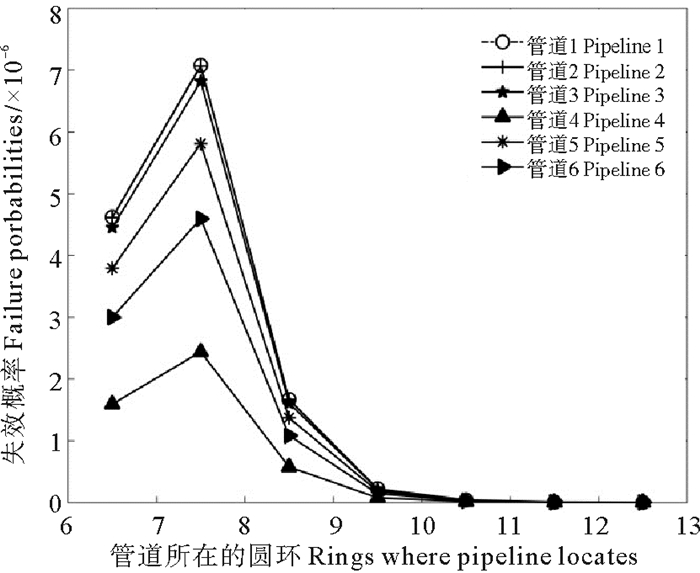
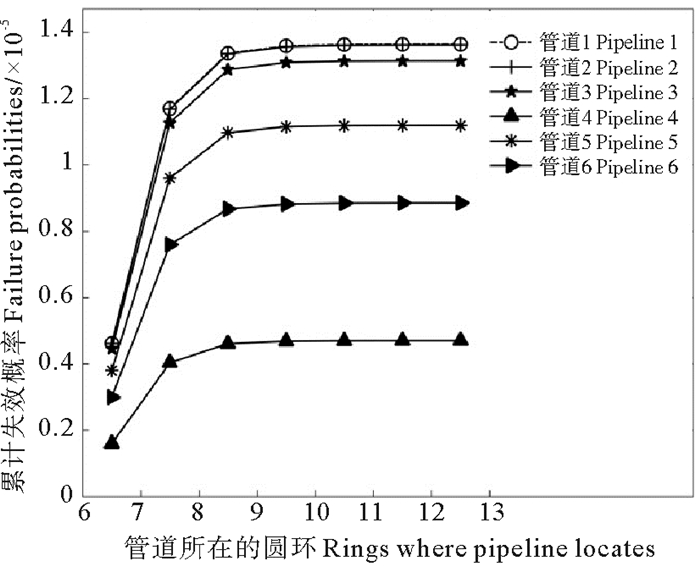
不同区域内管线段的失效概率存在差异:由船锚的漂移分布函数可知,船锚落在距坠落点较远区域内的概率较小,相应的管道失效概率也越小。为分析其影响,选取表 4中6种不同管道,计算距坠落点距离不同的区域内管线段的失效概率及累计失效概率,其结果如图 4、图 5所示。在距坠落点较近的区域内,失效概率随距离的增加而增大,并在第7、8个圆环之间的区域内达到最大,之后随距离的增加逐渐减小;累计失效概率起初随距离的增加而增大,随后几乎不变。由以上分析可知,在距坠落点较近区域内,管线受损风险较大,距坠落点较远区域内的管线受损风险较小。据此可采取合理防护措施,以降低风险、节省成本。
|
图 4 管道失效概率随距坠落点距离的变化 Fig. 4 Failure probabilities with different distances from dropped point |
|
图 5 管道累积失效概率随距坠落点距离的变化 Fig. 5 Accumulated failure probabilities with different distances from dropped point |
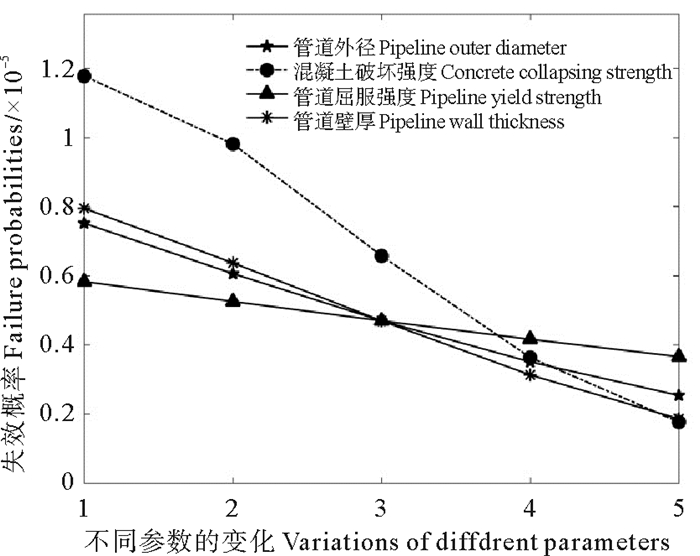
在求解管道失效概率时,将管径、管道壁厚、屈服强度、混凝土破坏强度作为随机变量来处理。其本身的变异性会影响管道的失效概率。现对其进行敏感性分析,以表 5中第4列参数为基准值,依次改变上述随机变量的取值,计算管道的失效概率,结果如图 6所示。由计算结果可知,随着上述随机变量取值的增大,管道的失效概率不断减小。其中,混凝土破坏强度对失效概率的影响最大,其次为管道外径及管道壁厚,管道屈服强度的影响最低。由以上分析可知,在管道尺寸、材料条件受限制无法改变的情况下,适当增加混凝土保护层的强度,可降低管道的受损风险。
|
|
表 5 随机变量的取值 Table 5 Values of stochastic variables |
|
图 6 管道失效概率随随机变量的变化 Fig. 6 Failure probabilities with different stochastic variables |
如何降低海底管道的受损风险是保证海洋油气资源开发的关键。基于可靠度理论,本文提出了海底管道受坠锚撞击作用下的失效概率计算方法。以某工程为实例,分析了影响管道失效概率的因素及管道受损风险,得到了以下结论:
(1) 以DNV法为基础,基于可靠度理论,提出了管道失效概率的计算方法。与DNV法相比,该方法可考虑坠物尺寸、质量及管道材料、尺寸对失效概率的影响,更符合实际情况,并通过实例进行了验证分析。
(2) 考虑各因素变异性的影响,确定了管道在船锚撞击作用下各区域内的失效概率及累积失效概率,给出了管道受损风险最大的区域,为采取防护措施提供技术参考。
(3) 探讨失效概率对各随机变量的敏感性,得到了影响坠锚撞击作用下管线失效概率的主要因素,为降低风险及管道优化设计提供理论依据。实际工程中,影响管道失效概率的因素很多,本文选取了其中的四个主要因素作为随机变量进行了分析。当统计资料充分时,应考虑其他因素变异性的影响,可得到更精确结果,进一步对管道进行优化设计。
| [1] |
DNV. Risk Assessment of Pipelines Protection(DNV-RP-F107)[S]. Oslo: Det Norske Veritas, 2010.
(  0) 0) |
| [2] |
Zeinoddini M, Harding J E, Parke G A R. Effect of impact damage on the capacity of tubular steel members of offshore structures[J]. Marine Structures, 1998, 11(4): 141-157.
(  0) 0) |
| [3] |
DNV. Submarine Pipeline System(DNV-OS-F101)[S]. Oslo: Det Norske Veritas, 2013.
(  0) 0) |
| [4] |
郭鸿雁, 朱伟. 基于事故树的海底管道第三方破坏风险分析[J]. 当代化工, 2013, 42(2): 212-214. GUO Hong-yan, ZHU Wei. Risk analysis on the third-party damages of submarine pipelines based on fault tree analysis[J]. Contemporary Chemical Industry, 2013, 42(2): 212-214. DOI:10.3969/j.issn.1671-0460.2013.02.030 (  0) 0) |
| [5] |
刘学涛, 张磊, 郭振邦, 等. 锚泊作业对海底管道撞击概率的研究[J]. 石油工程建设, 2005, 31(6): 30-33. LIU Xue-tao, ZHANG Lei, GUO Zhen-bang, et al. Impacting probability for pipeline in case of anchoring[J]. Petroleum Engineering Construction, 2005, 31(6): 30-33. DOI:10.3969/j.issn.1001-2206.2005.06.008 (  0) 0) |
| [6] |
丁红岩, 乐丛欢, 张浦阳. 落物撞击作用下海底管道风险评估[J]. 海洋工程, 2010, 28(1): 25-30. DING Hong-yan, LE Cong huan, ZHANG Pu-yang. Risk assessment of the submarine pipeline subjected to the dropped loads[J]. The Ocean Engineering, 2010, 28(1): 25-30. (  0) 0) |
| [7] |
王琮, 赵冬岩, 罗超. 基于概率的锚泊撞击对海底管道埋深影响分析[J]. 中国造船, 2010, 51(2): 89-94. WANG Cong, ZHAO Yan-dong, LUO Chao. Probability-based analysis for buried depth for the submarine pipeline impacted by the anchor[J]. Shipbuilding of China, 2010, 51(2): 89-94. (  0) 0) |
| [8] |
粟京. DNV96版《海底管道系统规范》对冲击防护的新规定[J]. 石油工业技术监督, 1999, 15(2): 15-17. SU Jing. New States of the shock protection in DNV96 version of marine pipe system standard[J]. Technology Supervision in Petroleum Industry, 1999, 15(2): 15-17. (  0) 0) |
| [9] |
Faravelli L. Response-surface approach for reliability analysis[J]. Journal of Engineering Mechanics, 1989, 115(12): 2763-2781. DOI:10.1061/(ASCE)0733-9399(1989)115:12(2763)
(  0) 0) |
| [10] |
中国国家标准化委员会中国人民共和国行业标准.霍尔锚(GB/T546-1997)[S].北京: 中国标准出版社, 1997. Standardization Administration of the People′s Republic of China. Professional Standard of the People's Republic of China. Hall anchor(GB/T546-1997)[S]. Beijing: China Standards Press, 1997. (  0) 0) |
 2019, Vol. 49
2019, Vol. 49


