海洋能作为一种储量丰富、开发前景广阔的可再生能源,近年来正逐渐成为关注热点[1-2]。海岛是中国海洋能发电的主要应用对象之一,海洋能发电可以解决海岛的供电问题,推动海岛经济发展,充分发挥海岛的战略地位,具有重要的经济与军事意义[3]。针对海岛海洋能开发存在的能流密度偏低、单一海洋能发电装置发电效率低、可靠性差等问题,海岛海洋能多能互补成为中国海洋能开发利用的重要发展方向[4]。横观国内外海洋能发展现状,目前国际上产业化程度最高的是海上风力发电,而国内波浪能发电处于示范化阶段[5],从资源、技术等角度考虑,风能与波浪能互补在可靠性、安全性、经济性和环境效益等方面表现优异,同时可以实现以风带浪,推动波浪能产业化进程[6]。
为推进海岛风浪互补电站开发,其前期决策尤其是选址决策至关重要,将直接影响未来的经济与社会效益。目前,国内外对风浪互补电站选址的研究较少。Margarita等[7]结合地理信息系统(Geographic information system,GIS)和多准则决策(Multi-criteria decision making,MCDM)方法,应用层次分析法(Analytic hierarchy process,AHP)求解评价指标的权重并进行方案排序,确定了在希腊克里特岛近海地区建造风浪互补电站的适宜区域。Cradden等[8]应用GIS中的决策支持工具进行风能与波浪能的资源分析,将资源数据可视化,研究结果表明欧洲北部和西部的资源条件符合要求、适宜开发。
目前,国内外学者对单一能源选址进行了大量研究,从风、浪资源角度考虑,主要集中在风电场的选址,对波浪能电站的选址研究较少。在风电场选址方面,Mahdy等[9]将GIS和AHP结合,应用简单加权法进行方案排序,绘制埃及海上风电场的适宜性地图,分级显示了红海附近适宜建造风电场的区域,为埃及海上风电场建设提供了参考。Kim等[10]将选址评价指标分类,利用GIS在大尺度上对韩国济州岛地区海上风电场可行区域进行了评价。Cavazzi等[11]应用一种基于GIS的工具来评估英国的海上风能潜力,该工具考虑到经济因素,例如开发成本、维护成本和生产收益等。Aymen等[12]从电网运行安全性、经济投资可行性以及站点容量性能等角度考虑,应用AHP结合GIS进行选址评估确定最佳海上风力发电场。Moradi等[13]应用GIS和AHP进行伊朗中部风资源的评估,从最不适宜到最适宜将场址适宜性程度划分为8个层次,结果表明研究区域的20%适合风电场开发。Hofer等[14]考虑到经济、政治和环境等方面,依托AHP与简单加权法得到风电场的区域适宜性指数,结合GIS得到德国亚琛市风电场开发适宜区域。Baseer等[15]应用AHP确定指标权重并在GIS中应用简单加权法确定方案适宜性指数,将其划分成六个层次以确定阿拉伯地区风电场的适宜开发区域。在波浪能电站选址方面,Ghosh等[16]首先依据AHP确定评价指标的权重,随后提出一种基于人工神经网络的MCDM方法确定英国和牙买加地区波浪能转换装置安放位置的适宜性指数。Abaei等[17]基于概率影响参数建立贝叶斯网络模型并将其扩展到影响图,提出一种新型选址决策方法来评估澳大利亚塔斯马尼亚州波浪能发电装置不同安放位置的预期效用。
由以上研究可知,目前风浪互补电站选址或风、浪单一能源电站选址主要集中在大尺度选址,即基于GIS或GIS与MCDM结合得到适宜性区划[18]。适宜性区划将可开发区域分为若干等级,并不能直接用于确定最优站址。因此风浪互补电站小尺度选址需进一步开展。
同时,目前电站选址的评价指标权重计算大多采用特征向量法(AHP的核心算法),即主观赋权法。特征向量法主要依靠专家的主观判断确定判断矩阵,因而难以避免主观偏差,进而影响权重及最终计算结果的客观性及鲁棒性。方案排序算法多采用简单加权法,因为其计算过程简单,可直接应用GIS工具进行求解,但其数学模型不够清晰[19]。
针对风浪互补电站选址决策领域存在的问题,本文提出海岛风浪互补电站小尺度选址决策方法,该方法包括决策模型构建和模型求解算法两部分。与大尺度选址决策方法相比,评价指标体系更复杂、全面,可以得出备选方案优先序列,直接服务于决策部门的最终站址选择,因此可以大大推动中国海洋能的产业化进程,为科学选址提供理论支撑。该方法在指标权重求解算法中采用组合权重法,将特征向量法和熵值法相结合,并引入集体决策理论,克服了单一主观赋权方法的弊端,降低主观偏差。在方案排序算法中选用TOPSIS方法,其数学意义明确,充分利用原始数据,减少信息损失。最后,将本方法应用于青岛市海岛风浪互补电站选址决策中,通过敏感性分析验证方法的科学性与鲁棒性。
1 海岛风浪互补电站选址决策模型构建海岛风浪互补电站选址决策所涉及的影响因素众多,根据文献综述法、专家调查法,结合风浪发电技术,构建模型评价指标集[20],包括资源条件、自然条件、经济因素和社会因素4个一级指标及其相应的15个二级指标。
1.1 资源条件指标资源条件指标是反映资源丰富程度及可开发程度的重要指标。本文根据风能、波浪能资源评估方法[21],建立资源条件二级指标集,包括年平均波功率密度、年平均有效波高、年有效波浪小时数、年平均风速、年平均风功率密度和年有效风小时数。其中,年平均波功率密度和年平均有效波高用于衡量波浪能潜在开发能力[22]。波功率密度和波高的原始数据拟通过SWAN计算模型得到,模型的输入为实际水深、风场等条件,波功率密度计算方法见公式(1)[23]。年平均风功率密度和年平均风速是衡量风能资源的重要指标,风场数据来源于欧洲中期天气预报中心(ECMWF)[23],风功率密度计算方法见公式(2)[24]。年有效波浪小时数和年有效风小时数影响波浪能和风能装置的运行时间[24]。
| $ P_{\text {wave }}=\frac{\rho g^{2} T_{\mathrm{E}}}{64000 \pi} H_{\mathrm{s}}^{2}。$ | (1) |
式中:Pwave为波功率密度(kW/m);ρ为海水密度,取1 025 kg/m3;Hs为有效波高(m);g为重力加速度,取9.798 m/s2;TE为能量周期(s)。
| $ P_{\text {wind }}=\frac{1}{2 n} \sum_{i=1}^{n} \rho \cdot v_{i}^{3}。$ | (2) |
式中:Pwind为风功率密度(W/m2);ρ为空气密度(kg/m3);n为设定时段内的记录数;vi为第i次记录的风速。
1.2 自然条件指标自然条件的优劣会对海岛风浪互补电站的建造难度、投资效益、运营风险等产生直接影响。自然条件指标的二级指标包括水深、潮差、海底地质和海岛地形。水深在一定程度上会限制风能、波浪能发电装置的类型和规模,同时会影响海底电缆布置的成本和安装工艺。潮差是指在一个潮汐周期内,相邻高潮位与低潮位之间的差值, 会影响风能、波浪能发电装置的设计、安装与运维。海底地质影响着安装发电装置和海底电缆的方式。海岛地形会影响岸上中央控制室和陆上电缆路由的设计。
1.3 经济因素指标经济因素指标影响海岛风浪互补电站的建造和运营成本,建立的二级指标包括总成本和国民生产总值。总成本旨在衡量海岛风浪互补独立电站建设的资金投入,包括电站的建设、运行和维护等费用[25]。国民生产总值反映了海岛的经济状况,国民生产总值越高,该海岛建设电站的需求程度越大。
1.4 社会因素指标社会因素指标的二级指标包括交通条件、与规划相符程度和电力需求匹配供给的程度。交通条件指航运条件及岛上交通状况,影响电站的安装和运维。与规划相符程度反映了当地相关政策对海岛的支持程度。电力需求与供给匹配程度可以根据当地人口,当前电力情况以及基础设施建设情况确定,反映了建设电站的紧迫程度。
基于评价指标集构建的海岛风浪互补电站选址决策模型如图 1所示。
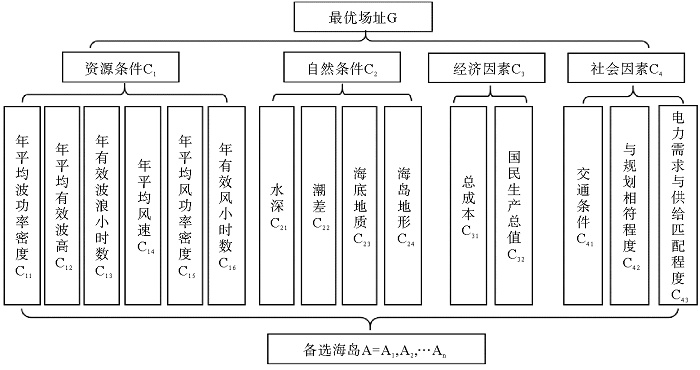
|
图 1 选址决策模型 Fig. 1 The decision-making model of site selection |
海岛风浪互补电站选址决策模型的评价指标具有定性与定量混杂、量纲不一致、指标值导向不一致等问题。根据评价指标的导向不同,可以将其分为效益型指标和成本型指标。在进行方案排序之前,需对指标体系进行规范化处理。通过1~9打分法实现定性指标的定量化和无量纲化。向量规范化法经验证是TOPSIS最适合的规范化方法[26],因此采用向量规范化法实现指标体系的规范化,如公式(3)~(4)所示[27]。
效益型指标:
| $ r_{i j}=\frac{x_{i j}}{\sqrt{\sum_{i=1}^{n} x_{i j}^{2}}}。$ | (3) |
成本型指标:
| $ r_{i j}=\frac{x_{i j}}{\sqrt{\sum_{i=1}^{n}\left(\frac{1}{x_{i j}}\right)^{2}}} 。$ | (4) |
式中:i=1, 2, …, m; j=1, 2, …, n;xij为第i个方案中第j个指标的属性值;rij为第i个方案中第j个指标规范后的属性值。
2 海岛风浪互补电站选址决策模型求解海岛风浪互补电站选址决策模型的求解算法主要包括权重求解算法和方案排序算法两大部分。
2.1 权重求解算法权重求解的方法通常包括主观赋权法和客观赋权法。由新能源选址决策文献综述[18]可知,目前应用最多的赋权方法是特征向量法。特征向量法根据专家对评价指标重要程度的主观判断形成判断矩阵,通过求解判断矩阵的特征值和特征向量得到评价指标的权重,计算结果受专家的主观判断支配,往往具有主观偏差。
为降低特征向量法的主观偏差,本文基于特征向量法、熵值法、集体决策理论建立组合赋权算法。其计算规则是将集体决策理论引入特征向量法计算一级指标权重,采用熵值法计算二级指标权重。相比单一特征向量法,该方法能够集合不同专家的偏好从而形成集体偏好,避免单个专家判断的主观偏差,使计算结果更趋于客观。另外,在考虑专家主观信息的同时能够充分利用指标属性值客观数据,根据数据的熵修正主观判断,从而进一步提高计算结果的准确性和鲁棒性。
2.1.1 特征向量法特征向量法(Eigenvector method)[28]由Saaty提出,是在可再生能源选址领域求解评价指标权重的最常用方法。通过特征向量法计算评价指标权重的过程如下:
(1) 构造判断矩阵。假设有n个评价指标,专家通过Saaty的1~9标度法[28]对每个评价指标进行两两比较判断其相对重要性,从而构建判断矩阵:
| $ \boldsymbol{B}=\left(b_{i j}\right)_{n \times n}。$ | (5) |
式中,bij为评价指标bi对评价指标bj的相对重要性。
(2) 计算判断矩阵的最大特征值及其相应的特征向量通过公式(6)求解判断矩阵的最大特征值及其相应的特征向量:
| $ \boldsymbol{B} w=\lambda_{\max }。$ | (6) |
式中:λmax为判断矩阵B的最大特征值; w为对应最大特征值的特征向量。
(3) 判断矩阵的一致性检验。为保证判断矩阵的一致性,需进行一致性检验。一致性检验可用一致性比率和一致性指标来衡量:
| $ C R=\frac{C I}{R I} $ | (7) |
| $ C I=\frac{\lambda_{\max }}{n-1}。$ | (8) |
式中: CR为一致性比率;CI为一致性指标;RI为随机一致性指标。RI根据n的数值由表 1确定。判断CR是否小于0.1,若小于则说明判断矩阵满足一致性要求,若不小于则说明不满足一致性要求,需要重新构建判断矩阵。
|
|
表 1 n阶矩阵的随机指标RI Table 1 RI of n-order matrix |
为使评价结果趋于客观,在评价指标权重的计算中引入集体决策理论,降低主观偏差[29]。设有l个专家,组成专家集E={E1, E2, …, El},其相应的权重为{e1, e2, …, el}。对于专家El,求解的评价指标权重为{w1, w2, …, wl}。则集体决策后的评价指标权重可由公式(9)计算得到:
| $ w_{l}=w_{i 1}^{e_{1}} w_{i 2}^{e_{2}} \cdots w_{i l}^{e_{l}}。$ | (9) |
熵值法是根据样本数据观测值的大小和相互之间的差异程度来计算指标权重[30]。熵越大意味着该评价指标对决策的影响越小,即该指标的权重越小。反之,熵越小意味着该评价指标对决策的影响越大,该指标的权重越大。用熵值法计算评价指标权重的过程如下:
(1) 计算第i个方案中第j个指标的比重:
| $ p_{i j}=\frac{r_{i j}}{\sum_{i=1}^{m} r_{i j}} 。$ | (10) |
式中:i=1, 2, …, m; j=1, 2, …, n;pij为第i个方案中第j个指标的比重。
(2) 计算第j个评价指标的熵值:
| $ E_{j}=-K \sum_{i=1}^{m} p_{i j} \ln p_{i j}; $ | (11) |
| $ K=\frac{1}{\ln m}。$ | (12) |
式中:i=1, 2, …, m; j=1, 2, …, n; Ej为第j个评价指标的熵值;K为系数。
(3) 计算第j个评价指标的权重:
| $ w_{j}=\frac{1-E_{j}}{\sum_{j=1}^{n}\left(1-E_{j}\right)}。$ | (13) |
式中,wj为第j个评价指标的权重。
2.1.4 组合权重法针对海岛风浪互补电站选址决策模型,提出组合权重法。其计算规则是分别求解一级指标和二级指标的权重,其中一级指标权重通过特征向量法、集体决策方法计算,二级指标权重通过熵值法计算,最后通过公式(14)求解组合权重:
| $ w_{c i j}^{\prime}=w_{c i} \times w_{c i j} $ | (14) |
式中:w′cij为指标的组合权重;wci为一级指标组合权重;wcij为二级指标组合权重。
2.2 方案排序算法在几何意义上,TOPSIS旨在选取与理想方案的欧几里德距离最短的方案,更为直观地展现排序结果[31],数学模型清晰。TOPSIS的计算原理为分别求解各备选方案与正理想解和负理想解之间的欧式距离计算相对贴近度,进而对备选方案进行排序。具体计算步骤如下:
(1) 求解加权规范化决策矩阵:
| $ \begin{gathered} \boldsymbol{V}=\left(v_{i j}\right)_{m \times n}=\left[\begin{array}{cccc} v_{11} & v_{12} & \cdots & v_{1 n} \\ v_{21} & v_{22} & \cdots & v_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ v_{m 1} & v_{m 2} & \cdots & v_{m n} \end{array}\right], \\ v_{i j}=w^{\prime}{ }_{i j} \times r_{i j} 。\end{gathered} $ | (15) |
式中:i=1, 2, …, m; j=1, 2, …, n;vij为第i个方案中第j个指标的加权规范化属性值;w′cij为指标的组合权重;rij为公式(1)和(2)中求得的指标规范后的属性值。
(2) 确定正理想解和负理想解。正理想解由加权规范化决策矩阵V中每列的最大值组成,用A+表示;相反,负理想解由V中每列的最小值组成,用A-表示:
| $ \boldsymbol{A}^{+}=\left[v_{1}^{+}, v_{2}^{+}, \cdots, v_{n}^{+}\right], v_{j}^{+}=\max \left(v_{i j}\right) ; $ | (16) |
| $ \boldsymbol{A}^{-}=\left[v_{1}^{-}, v_{2}^{-}, \cdots, v_{n}^{-}\right], v_{j}^{-}=\min \left(v_{i j}\right) 。$ | (17) |
式中:i=1, 2, …, m; j=1, 2, …, n。
(3) 计算欧式距离。利用公式(18)~(19)计算各备选方案与正理想解和负理想解的距离:
| $ D_{i}^{+} =\sqrt{\sum_{j=1}^{n}\left(v_{i j}-v_{j}^{+}\right)^{2}} ; $ | (18) |
| $ D_{i}^{-} =\sqrt{\sum_{j=1}^{n}\left(v_{i j}-v_{j}^{-}\right)^{2}} $ | (19) |
式中:Di+为各备选方案与正理想解的距离;Di-为各备选方案与负理想解的距离。
(4) 计算相对贴近度并对备选方案进行排序。通过公式(20)计算各个备选方案的相对贴近度。相对贴近度越大,方案越优;相对贴近度越小,方案越劣。相对贴近度最大的方案为最优方案:
| $ C_{i}=\frac{D_{i}^{-}}{D_{i}^{-}+D_{i}^{+}} $ | (20) |
式中Ci为第i个备选方案的相对贴近度。
3 应用实例青岛市所辖海岛120个,有居民海岛7个[32],海岛总面积约占15.04 km2,海岛海岸线长度约达122.92 km。海岛风、浪资源丰富,目前海岛电力资源紧缺,海岛风浪互补电站可以极大缓解海岛用电问题[33]。将本文提出的海岛风浪互补电站选址决策方法应用于青岛市海岛风浪互补电站选址决策中。
3.1 建立选址决策模型根据青岛市风浪互补大尺度选址[34]的结果及文献调研、实地调查,确定出4个备选海岛,分别为女岛、小麦岛、竹岔岛和三平岛,构成备选方案集A={A1, A2, A3, A4}。通过数据调查、现场观测及数值模拟等手段,得到各方案评价指标的属性值如表 2所示。其中,资源条件指标数据来源及计算方法见1.1,均为定量指标。自然条件指标中,水深数据来源于大洋地势图[35],潮差数据来源于《中国近海海洋图集(山东省海岛海岸带)》[36],海底地质数据来源于《中国近海海洋图集(海底地形地貌)》[37],海岛地形数据来源于《中国海岛志(山东卷)》[38],均为定性指标,采用专家打分法得到。经济因素指标中,总成本根据离岸距离、离港距离、海底电缆铺设费用和装置费用等预估,国民生产总值数据来源于《中国海岛志(山东卷)》[38],均为定量指标。社会因素指标中,交通条件数据来源于《山东省海洋功能区划》[39],与规划相符程度数据来源于《青岛市海岛保护规划》[32],电力需求与供给匹配程度数据来源于《中国海岛志(山东卷)》[38]以及政府公开发布的统计年鉴,均为定性指标,采用专家打分法得到。
|
|
表 2 属性值矩阵 Table 2 Attribute value matrix |
对定性指标进行定量化处理后,进一步经过向量规范化法对指标进行规范化处理,得到规范化决策矩阵(见表 3)。
|
|
表 3 规范化决策矩阵 Table 3 Standardized decision matrix |
基于特征向量法和集体决策方法求解一级指标权重。将15位专家分为5组,记为E={E1, E2, E3, E4, E5},权重为{0.3, 0.3, 0.2, 0.1, 0.1}。根据1~9标度法,各专家组对评价指标集的判断矩阵依次为:
| $ \boldsymbol{B}_{1}=\left[\begin{array}{cccc} 1 & 5 & 3 & 6 \\ 1 / 5 & 1 & 1 / 3 & 2 \\ 1 / 3 & 3 & 1 & 3 \\ 1 / 6 & 1 / 2 & 1 / 3 & 1 \end{array}\right], \boldsymbol{B}_{2}=\left[\begin{array}{cccc} 1 & 5 & 3 & 7 \\ 1 / 5 & 1 & 1 / 3 & 2 \\ 1 / 3 & 3 & 1 & 4 \\ 1 / 7 & 1 / 2 & 1 / 4 & 1 \end{array}\right], \\ \begin{aligned} \boldsymbol{B}_{3} &=\left[\begin{array}{cccc} 1 & 5 & 4 & 7 \\ 1 / 5 & 1 & 1 / 2 & 3 \\ 1 / 4 & 2 & 1 & 3 \\ 1 / 7 & 1 / 3 & 1 / 3 & 1 \end{array}\right], \boldsymbol{B}_{4}=\left[\begin{array}{cccc} 1 & 6 & 4 & 5 \\ 1 / 6 & 1 & 1 / 2 & 2 \\ 1 / 4 & 2 & 1 & 2 \\ 1 / 5 & 1 / 2 & 1 / 2 & 1 \end{array}\right], \\ \boldsymbol{B}_{5} &=\left[\begin{array}{cccc} 1 & 4 & 2 & 5 \\ 1 / 4 & 1 & 1 / 2 & 3 \\ 1 / 2 & 2 & 1 & 4 \\ 1 / 5 & 1 / 3 & 1 / 4 & 1 \end{array}\right]。\end{aligned} $ | (21) |
计算得到各判断矩阵的最大特征值、一致性指标、一致性比率等如表 4所示。经验证CR <0.1,所有判断矩阵均满足一致性要求,故表 5所示结果即为各专家组确定的一级指标权重。经公式(9)得到5个专家组的集体决策结果,故海岛风浪互补电站选址决策模型的一级指标权重为(0.576 2, 0.119 6, 0.233 5, 0.070 7)。由计算结果可知,资源条件指标所占权重大于50%,是最重要的指标,在选址过程中应着重考虑。经济因素指标权重为23.35%,仅次于资源条件指标。自然条件指标和社会因素指标权重分别为11.96%和7.07%,重要性稍低。
|
|
表 4 一致性检验 Table 4 Consistency check |
|
|
表 5 各专家组的一级权重 Table 5 The first-level criteria weight of each expert group |
二级指标权重基于熵值法求解,通过公式(10)~(13)计算,计算结果见表 6。由计算结果可知,资源条件指标中波浪能相关的二级指标权重C11、C12、C13远大于风能相关的二级指标C14、C15、C16,表明波浪能资源的优劣对选址的影响更大。自然条件指标中水深C21的权重占比约68%,说明其在自然条件指标中的绝对重要性。在经济因素指标中,国民生产总值C32的熵远小于总成本C31的熵,因此其权重远大于总成本权重。社会因素指标中,交通条件C41和电力需求与规划相符程度C43指标权重相对较大。
|
|
表 6 熵值法计算结果 Table 6 Calculation result of entropy method |
根据公式(14)求得组合权重见表 7。通过分析计算结果发现,年有效波高权重最大,为20.92%,可见波浪能资源条件的优劣对选址决策起着至关重要的作用。国民生产总值权重为23.16%,表明当地的经济发展状况对选址决策有较大影响。与此同时,自然条件指标和社会因素指标权重相对较小,该两个一级指标下的所有指标权重均不超过10%,对整体选址决策的影响较小。
|
|
表 7 组合权重 Table 7 Combined weight |
由规范化后各指标的属性值以及各评价指标的组合权重,求得加权规范化决策矩阵V=[V1, V2, V3, V4]。
| $ \begin{aligned} &\boldsymbol{V}_{1}=\left[\begin{array}{lllllll} 0.0408 & 0.1396 & 0.0294 & 0.0132 & 0.0601 & 0.0101 & \\ 0.0413 & 0.1434 & 0.0304 & 0.0134 & 0.0625 & 0.0100 & \\ 0.0415 & 0.1508 & 0.0315 & 0.0126 & 0.0547 & 0.0098 & \\ 0.0376 & 0.1231 & 0.0288 & 0.0129 & 0.0589 & 0.0097 & \end{array}\right], \\ &\boldsymbol{V}_{2}=\left[\begin{array}{llllll} 0.0349 & 0.0067 & 0.0049 & 0.0056 & \\ 0.0627 & 0.0094 & 0.0056 & 0.0074 & \\ 0.0279 & 0.0067 & 0.0042 & 0.0056 & \\ 0.0279 & 0.0067 & 0.0042 & 0.0074 & \end{array}\right] \text {, }\\ &\boldsymbol{V}_{3}=\left[\begin{array}{llll} 0.0009 & 0.0397 & \\ 0.0011 & 0.0227 & \\ 0.0009 & 0.2270 & \\ 0.0009 & 0.0057 & \end{array}\right], \\ &\boldsymbol{V}_{4}=\left[\begin{array}{lllll} 0.0127 & 0.0011 & 0.0239 & \\ 0.0229 & 0.0009 & 0.0143 & \\ 0.0102 & 0.0009 & 0.0239 & \\ 0.0127 & 0.0009 & 0.0095 & \end{array}\right] \circ \end{aligned} $ | (22) |
通过公式(16)~(19)分别求得正理想解、负理想解及各方案相应的欧式距离,如表 8、9所示。通过公式(19)求得各备选海岛的相对贴近度C=(0.179 7, 0.186 0, 0.854 6, 0.022 5),故A3(竹岔岛)>A2(小麦岛)>A1(女岛)>A4(三平岛)。竹岔岛由于其波浪能资源最优,国民生产总值最高,其相对贴近度远大于其他三个海岛。因此,竹岔岛为青岛市建设海岛风浪互补电站的首选海岛。
|
|
表 8 正理想解与负理想解 Table 8 Positive and negative ideal solutions |
|
|
表 9 备选方案与正理想解、负理想解的欧式距离 Table 9 Euclidean distance between alternatives and positive and negative ideal solutions |
为检验计算结果的鲁棒性并验证决策方法的可行性和科学性,进一步对计算结果进行敏感性分析。敏感性分析通过改变评价指标的权重进行,包括三个方面:一级指标权重相等,二级指标权重不变;一级指标权重不变,二级指标权重相等;忽略各指标之间的差异性,使各指标的权重相等。计算结果分别见表 10~12。
|
|
表 10 一级指标等权下各指标组合权重 Table 10 Combined weight of criteria under the equal weight of the first-level-criteria |
|
|
表 11 二级指标等权下各指标组合权重 Table 11 Combined weight of criteria under the equal weight of the second-level-criteria |
|
|
表 12 各指标组合权重相等 Table 12 Combined weight of criteria is equal |
根据变化后的各指标权重,求得各方案的相对贴近度及排序结果如表 13所示。从计算结果可以看出,随着指标权重的变化,方案相对贴近度发生变化,但方案排序结果没有变化,故在一定程度上验证了该方法的鲁棒性。因此本文提出的海岛风浪互补电站选址决策方法具有较强的可行性与稳定性。
|
|
表 13 敏感性分析结果对比 Table 13 Comparison of sensitivity analysis results |
海岛风浪互补电站可以有效缓解海岛的供电问题,推动海洋经济发展,强化海岛的军事与战略地位。针对电站建设的先决条件及关键问题,本文基于MCDM提出了海岛风浪互补电站选址决策方法,并将其应用于青岛市海岛风浪互补电站选址决策中。
该方法建立的选址决策模型包括资源条件、自然条件、经济因素和社会因素4个一级指标及相应的12个二级指标,求解算法计算方案优先开发序列,能够为最优站址决策提供直接的理论参考,进而有效指导实际工程。在权重求解算法中,结合集体决策理论提出基于熵值法和特征向量法的组合权重法,改进了传统主观赋权法,有效降低主观偏差并提高计算结果的鲁棒性。方案排序算法采用TOPSIS,数学模型更加清晰。本文提出的海岛风浪互补电站选址决策方法可以为中国海洋能电站微观选址提供理论支撑,推进海洋能的产业化进程。
计算结果表明,青岛市海岛风浪互补电站优先开发序列为竹岔岛、小麦岛、女岛、三平岛,最优站址为竹岔岛,经敏感性分析验证了方法的鲁棒性和科学性。计算结果可以直接指导青岛市海岛风浪互补电站建设,为科学决策提供依据。
| [1] |
Aleixandre-Tudó J L, Castelló-Cogollos L, Aleixandre J L, et al. Renewable energies: Worldwide trends in research, funding and international collaboration[J]. Renewable Energy, 2019, 139: 268-278. DOI:10.1016/j.renene.2019.02.079 (  0) 0) |
| [2] |
Sun J W, Hu S L J, Li H J. Laplace domain method for computing the transient response of floating structures to irregular wave[J]. Ocean Engineering, 2020, 203: 107200. DOI:10.1016/j.oceaneng.2020.107200 (  0) 0) |
| [3] |
国家海洋局. 全国海洋经济发展"十三五"规划[EB/OL]. (2017-05-04)[2017-09-07]. http://images.mofcom.gov.cn/www/201709/20170907170048332.pdf. State Oceanic Administration. The 13th Five-Year Plan for National Marine Economic Development[EB/OL]. (2017-05-04)[2017-09-07]. http://images.mofcom.gov.cn/www/201709/20170907170048332.pdf. (  0) 0) |
| [4] |
乌云娜, 杨益晟, 冯天天, 等. 风光互补电站宏观选址研究[J]. 电网技术, 2013, 37(2): 319-326. Wu Y N, Yang Y S, Feng T T, et al. Research on macro-site selection of wind-solar hybrid power station[J]. Power System Technology, 2013, 37(2): 319-326. (  0) 0) |
| [5] |
王项南, 贾宁, 薛彩霞, 等. 关于我国海洋可再生能源产业化发展的思考[J]. 海洋开发与管理, 2019, 12: 14-18. Wang X N, Jia N, Xue C X, et al. Thinking about the industrialization development of marine renewable energy in my country[J]. Ocean Development and Management, 2019, 12: 14-18. (  0) 0) |
| [6] |
章凯, 陈博. "多能互补"技术发展与应用[J]. 科技和产业, 2018, 18(11): 92-99. Zhang K, Chen B. The development and application of "Multiple Complementary"[J]. Science Technology and Industry, 2018, 18(11): 92-99. DOI:10.3969/j.issn.1671-1807.2018.11.018 (  0) 0) |
| [7] |
Margarita V, Eva L, Dimitra G, et al. GIS-based multi-criteria decision analysis for site selection of hybrid offshore wind and wave energy systems in Greece[J]. Renewable and Sustainable Energy Reviews, 2017, 73: 745-757. DOI:10.1016/j.rser.2017.01.161 (  0) 0) |
| [8] |
Cradden L, Kalogeri C, Martinez Barrios I, et al. Multi-criteria site selection for offshore renewable energy platforms[J]. Renewable Energy, 2016, 87: 791-806. DOI:10.1016/j.renene.2015.10.035 (  0) 0) |
| [9] |
Mahdy M, Bahaj A S. Multi criteria decision analysis for offshore wind energy potential in Egypt[J]. Renewable Energy, 2018, 118: 278-289. DOI:10.1016/j.renene.2017.11.021 (  0) 0) |
| [10] |
Kim T, Park J L, Maeng J. Offshore wind farm site selection study around Jeju Island, South Korea[J]. Renewable Energy, 2016, 94: 619-628. DOI:10.1016/j.renene.2016.03.083 (  0) 0) |
| [11] |
Cavazzi S, Dutton A. An offshore wind energy Geographic Information System (OWE-GIS) for assessment of the UK's offshore wind energy potential[J]. Renewable Energy, 2016, 87: 212-228. DOI:10.1016/j.renene.2015.09.021 (  0) 0) |
| [12] |
Aymen C, Catalin F C, Mircea A. Multi-criteria selection of offshore wind farms: Case study for the Baltic States[J]. Energy Policy, 2017, 103: 179-192. DOI:10.1016/j.enpol.2017.01.018 (  0) 0) |
| [13] |
Moradi S, Yousefi H, Noorollahi Y, et al. Multi-criteria decision support system for wind farm site selection and sensitivity analysis: Case study of Alborz Province, Iran[J]. Energy Strategy Reviews, 2020, 29: 1-17. (  0) 0) |
| [14] |
Höfer T, Sunak Y, Siddique H, et al. Wind farm siting using a spatial Analytic Hierarchy Process approach: A case study of the Städteregion Aachen[J]. Applied Energy, 2016, 163: 222-243. DOI:10.1016/j.apenergy.2015.10.138 (  0) 0) |
| [15] |
Baseer M A, Rehman S, Meyer J P, et al. GIS-based site suitability analysis for wind farm development in Saudi Arabia[J]. Energy, 2017, 141: 1166-1176. DOI:10.1016/j.energy.2017.10.016 (  0) 0) |
| [16] |
Ghosh S, Chakraborty T, Saha S, et al. Development of the location suitability index for wave energy production by ANN and MCDM techniques[J]. Renewable and Sustainable Energy Reviews, 2016, 59: 1017-1028. DOI:10.1016/j.rser.2015.12.275 (  0) 0) |
| [17] |
Abaei M M, Arzaghi E, Abbassi R, et al. Developing a novel risk-based methodology for multi-criteria decision making in marine renewable energy applications[J]. Renewable Energy, 2017, 102: 341-348. DOI:10.1016/j.renene.2016.10.054 (  0) 0) |
| [18] |
Shao M, Han Z X, Sun J W, et al. A review of multi-criteria decision making applications for renewable energy site selection[J]. Renewable Energy, 2020, 157: 377-403. DOI:10.1016/j.renene.2020.04.137 (  0) 0) |
| [19] |
Shahabi H, Keihanfard S, Ahmad B B, et al. Evaluating Boolean, AHP and WLC methods for the selection of waste landfill sites using GIS and satellite images[J]. Environmental Earth Sciences, 2014, 71: 4221-4233. DOI:10.1007/s12665-013-2816-y (  0) 0) |
| [20] |
邵萌, 史宏达, 赵阳, 等. 基于改进层次分析法的海洋能多能互补选址决策模型[J]. 太阳能学报, 2016, 37(9): 2443-2450. Shao M, Shi H D, Zhao Y, et al. Location decision model of hybrid marine energy based on improves AHP method[J]. Acta Energiae Solaris Sinica, 2016, 37(9): 2443-2450. DOI:10.3969/j.issn.0254-0096.2016.09.040 (  0) 0) |
| [21] |
韩林生, 王静, 高佳, 等. 山东褚岛北部海域波浪能资源分析[J]. 太阳能学报, 2020, 41(2): 165-171. Han L S, Wang J, Gao J, et al. Analysis of wave energy resources in the north sea of Dongchu Island[J]. Acta Energiae Solaris Sinica, 2020, 41(2): 165-171. (  0) 0) |
| [22] |
Qiu S, Liu K, Wang D, et al. A comprehensive review of ocean wave energy research and development in China[J]. Renewable & Sustainable Energy Reviews, 2019(113): 109-271. (  0) 0) |
| [23] |
Liang B, Gao H, Shao Z. Characteristics of global waves based on the third-generation wave model SWAN[J]. Marine Structures, 2019, 64: 35-53. DOI:10.1016/j.marstruc.2018.10.011 (  0) 0) |
| [24] |
王静, 曹洁, 邱粲, 等. 山东沿海风能资源分布特征及评估[J]. 南京信息工程大学学报(自然科学版), 2014, 6(4): 342-348. Wang J, Cao J, Qiu C, et al. Distribution characteristics and evaluation of wind energy resources along the coast of Shandong[J]. Journal of Nanjing University of Information Technology (Natural Science Edition), 2014, 6(4): 342-348. (  0) 0) |
| [25] |
徐狄锷. 光伏电站项目效益分析及风险评估[J]. 经济研究导刊, 2020, 22: 82-83. Xu D E. Project benefit analysis and risk assessment of photovoltaic power station[J]. Economic Research Guide, 2020, 22: 82-83. (  0) 0) |
| [26] |
Chen P. Effects of normalization on the entropy-based TOPSIS method[J]. Expert Systems with Applications, 2019, 136: 33-41. DOI:10.1016/j.eswa.2019.06.035 (  0) 0) |
| [27] |
廖炎平, 刘莉, 邢超. TOPSIS中不同规范化方法的研究[J]. 北京理工大学学报, 2012, 32(5): 871-880. Liao Y P, Liu L, Xing C. Investigation of different normalization methods for TOPSIS[J]. Transactions of Beijing Institute of Technology, 2012, 32(5): 871-880. (  0) 0) |
| [28] |
Satty T L. The Analytic Hierarchy Process[M]. New York: McGraw-Hill, 1980.
(  0) 0) |
| [29] |
Wu Y N, Zhang T, Xu C B, et al. Optimal location selection for offshore wind-PV-seawater pumped storage power plant using a hybrid MCDM approach: A two-stage framework[J]. Energy Conversion and Management, 2019, 199: 112-130. (  0) 0) |
| [30] |
熊黑钢, 付金花, 王凯龙. 基于熵权法的新疆奇台绿洲水资源承载力评价研究[J]. 中国生态农业学报, 2012, 20(10): 1383-1387. Xiong H G, Fu J H, Wang K L. Evaluation of water resource carrying capacity of Qitai Oasis in Xinjiang by entropy method[J]. Chinese Journal of Eco-Agriculture, 2012, 20(10): 1383-1387. (  0) 0) |
| [31] |
Hwang C L, Yoon K. Multiple Attribute Decision Making: Methods and Applications[M]. Berlin: Springer-Heidelberg, 1981.
(  0) 0) |
| [32] |
青岛市海洋与渔业局. 青岛市海岛保护规划[EB/OL]. (2015-10-24)[2016-06-21]. http://ocean.qingdao.gov.cn/n12479801/n12480082/160621093005256828.html Qingdao Ocean and Fishery Bureau. Qingdao Island Protection Planning[EB/OL]. (2015-10-24)[2016-06-21]. http://ocean.qingdao.gov.cn/n12479801/n12480082/160621093005256828.html (  0) 0) |
| [33] |
Magagna D, Uihlein A. Ocean energy development in Europe: Current status and future perspectives[J]. International Journal of Marine Energy, 2015, 11: 84-104. (  0) 0) |
| [34] |
Shao M, Han Z X, Sun J W, et al. A GIS-MCDM combination for the site assessment of wave energy power station in Qingdao, Eastern China[C] //Proceedings of the 30st ISOPE Conference. Shanghai: International Society of Offshore and Polar Engineers, 2020: 137-143.
(  0) 0) |
| [35] |
国际海道测量局. 大洋地势图[EB/OL]. (2003-04-07)[2017-04-18]. https://max.book118.com/html/2017/0415/100371018.shtm International Hydrographic Bureau. Map of Ocean Topography[EB/OL]. (2003-04-07)[2017-04-18]. https://max.book118.com/html/2017/0415/100371018.shtm (  0) 0) |
| [36] |
山东省海洋与渔业厅. 中国近海海洋图集: 山东省海岛海岸带著[M]. 北京: 海洋出版社, 1999. Department of Oceans and Fisheries of Shandong Province. China Offshore Marine Atlas: Coastal Belts of Islands in Shandong Province[M]. Beijing: Ocean Press, 1999. (  0) 0) |
| [37] |
国家海洋局. 中国近海海洋图集: 海底地形地貌[M]. 北京: 海洋出版社, 2006. State Oceanic Administration. China Offshore Ocean Atlas: Seabed Topography[M]. Beijing: Ocean Press, 2006. (  0) 0) |
| [38] |
《中国海岛志》编纂委员会. 中国海岛志(山东卷)[M]. 北京: 海洋出版社, 2013. Compilation Committee of "Chinese Islands History". Chinese Islands History (Shandong Volume)[M]. Beijing: Ocean Press, 2013. (  0) 0) |
| [39] |
山东省生态环境厅. 山东省海洋生态环境保护规划[EB/OL]. (2019-02-25)[2019-03-14]. http://www.eshian.com/laws/45841.html Shandong Provincial Department of Ecology and Environment. Marine Ecological Environmental Protection Planning of Shandong Province[EB/OL]. (2019-02-25)[2019-03-14]. http://www.eshian.com/laws/45841.html (  0) 0) |
 2022, Vol. 52
2022, Vol. 52


