2. 中国海洋大学海洋工程学院,山东 青岛 266100
水下传动装置稳定运转是新型海洋装备有效服役的关键之一,海洋环境下各类杂质不断进入高强钢制传动轴的小间隙配合面,硬质颗粒(主要为韧性金属颗粒)因配合面运动而挤入间隙并产生应力集中,引起配合面损伤乃至嵌入间隙;海洋环境下传动装置配合面蚀难以避免,无磨粒磨损情况下对整体性能影响有限,但是传动过程中磨粒与含腐蚀配合面间局部应力场可能产生复杂变化,而局部应力三轴度变化对韧性金属损伤演化影响显著[1-2],很可能影响配合面磨粒磨损[3]过程,从而加速装置传动性能退化;另外,新型装备入水出水循环过程必然存在温差,也将改变磨粒与配合面之间的应力状态及磨损过程,从而影响装置传动性能。因此,综合考虑海洋环境腐蚀-温度变化-金属颗粒共同作用,建立水下传动装置磨粒-配合面-传动轴间传动-承载-损伤耦合模型与计算方法,对于水下传动装置故障机理探索与优化设计更新都有直接的理论意义和工程价值。
磨粒磨损为磨粒与韧性钢材配合面中表面材料损伤剥落过程[4-5]。早期磨粒磨损的计算大多基于Rabinowicz建立的关于磨粒磨损的经典模型,给出了简化模型和数学表达式,其中基本假设为:(1)将经受磨损的材料简化成一种不产生任何塑性变形的绝对刚体;(2)将硬质磨粒简化成一个圆锥体;(3)将磨损过程视为简单的滑动过程[6-7]。经典模型忽略了磨粒磨损过程中材料的永久变形与断裂破坏[8],所以建立的的模型与实际差距较大,无法描述磨损面沟壑的产生以及磨粒的破碎。为解决以上问题,Barge[9]等提出了磨粒磨损中的犁沟模型,研究了较硬的圆头形磨粒在较软表面的犁沟切削过程,获得了载荷、材料和磨粒的硬度等因素对表面应力分的影响。但是,这类模型采用传统的韧性金属塑性模型,对应本构多基于标准单轴拉伸试验构建,未反应三轴应力[10]作用下材料破坏特征,也就无法反映挤压磨损过程中磨粒和磨损面上复杂的应力变化,未能全面得到磨粒磨损塑性破坏的过程与机制,也就无法研究腐蚀导致金属表面形貌微小变化对磨损破坏的影响。目前,塑性研究已确认复杂多轴作用下产生各类应力组合,对于材料失效特征及阈值影响显著[11],而且韧性材料受力过程中承载截面上孔洞不断萌生并扩展,使得有效承载截面积不断减小,韧性材料损伤演化至失效过程不同于传统的简化塑性模型(例如理想弹塑性)预测。由上可见,韧性损伤是微细观塑性累积过程,复杂应力作用下韧性损伤过程会更远离简化塑性模型预测,忽略应力三轴度及损伤演化的磨粒磨损计算对于水下关键结构性能变化的预测可能产生偏差。
海洋环境磨损、腐蚀与温差共同作用下水下传动装置小间隙配合面很可能存在复杂应力作用下损伤演化过程。为更好反映海洋环境小间隙传动配合面中磨粒磨损过程,本文采用基于不可逆热力学原理的材料损伤演化模型,发展了基于状态变量的数值计算方法,实现了有限元软件ABAQUS的二次开发,为更好的反映工程中磨粒状况,设计三维球形分形模型[12],实现了磨粒与接触表面微观接触过程中三维复杂应力[13-14]演化过程的有效计算,由此分析了接触表面的应力分布演化以及对传动装置转动的影响。基于以上模型的计算结果,探索海洋环境下传动装置磨损及性能退化机理,获得腐蚀与温度变化[15]对磨粒磨损与传动性能过程的影响。整体上发展了基于金属韧性损伤理论的传递结构配合面损伤机理及传动性能建模与模拟,实现了材料塑性损伤、配合面磨损与传动装置性能分析一体化,获得了不同环境条件下配合面损伤机制。
1 复杂应力下韧性金属损伤演化模型工程实际磨粒磨损中,配合面出现沟犁、磨粒局部扁平,具有典型的塑性损伤特征,这一过程中材料内部主要是微孔洞和微裂纹的形成和扩展,使其产生大塑性变形乃至断裂,从而使配合面和磨粒出现永久变形和破坏。因此,这里引入损伤变量以合理描述以上物理过程,工程实际中配合面和磨粒为韧性金属,都是各向同性的连续介质,因此可以用一个标量来描述因微孔洞和微裂纹导致的连续介质有效承载面积的减小,这里用D表示,定义:
| $ D=1-\frac{A_{\mathrm{e}}}{A} 。$ | (1) |
式中:A是截面总面积;Ae是有效承载面积。磨粒磨损中颗粒与摩擦面都承受强非比例载荷作用,将显著影响结构损伤与破坏速度与程度,从而改变传动装置运行性能。为在数值计算中有效描述复杂多轴应力场中韧性金属破坏,进而获得传动装置运行特性演化过程,这里采用基于不可逆热力学的韧性金属损伤耗散势,由广义正则化法则导出损伤材料的本构方程及损伤演化方程[16],其结果如下,
| $ D=D_{\mathrm{c}}-\left(D_{\mathrm{c}}-D_{0}\right)\left[1-\frac{p}{\varepsilon_{c}} f^{\frac{1}{\alpha}}\left(\frac{\sigma_{m}}{\sigma_{e}}\right)\right]^{\alpha} 。$ | (2) |
式中:
为在有限元软件实现复杂应力下材料破坏与传动结构磨损计算,Fortran编译了韧性金属损伤演化计算程序并导入ABAQUS求解器;模拟中可实现:细观上,磨粒与配合面接触区内材料弹性与塑性极限随损伤退化,损伤达到阈值后单元失效实现磨损剥离;宏观上,以配合面转角与驱动力关系表征装置传动性能变化规律,循环驱动力作用下配合面不可恢复转动角度增大表明传动性能下降;通过磨粒-配合面-传动轴一体化建模下细观损伤与宏观传动耦合模拟,将磨粒磨损的细观破坏机理与装置传动性能相关联,可实施装置磨损故障的机理研究。通过子程序精细计算磨粒及传动装置的损伤,在循环加载过程中实时更新单元损伤与退化,程序编制思路与计算流程如图 1所示,简述如下:
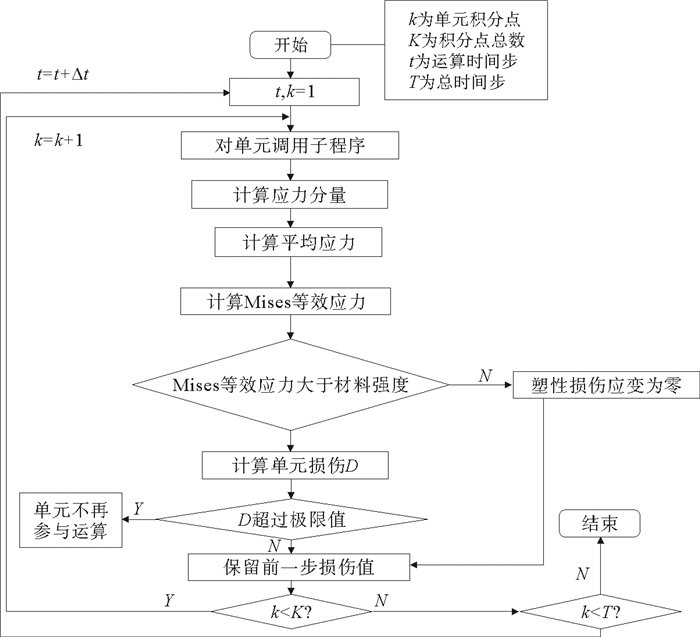
|
图 1 计算流程图 Fig. 1 Flow chart of calculation |
(1) 计算得到正应力及切应力等6个应力分量,计算得到Mises等效应力,这是子程序主要参数及计算塑性损伤量累计的判据。
(2) 子程序编译中,参数使用ABAQUS可识别的状态变量,利用状态变量能够保障参数准确传递。
(3) 根据不断更新的Mises等效应力与材料强度作数据比较,如果应力大于材料强度时,产生了塑性损伤,根据损伤演化方程计算损伤。
(4) 根据数据循环不断更新并累积塑性损伤,当损伤达到一定程度时,认为此单元材料已经遭到破坏,于模型中将该单元删除。
为了验证程序的正确性,数值模拟了韧性金属的标准单轴拉伸试验,计算模型如图 2(a)所示,试样参数与规范实验一致,模型一端固定,另一端施加位移荷载,数值模拟与实验结果进行对比(见图 2(b)、(c)):两者基本吻合,验证了材料子程序和计算设置能够实现单元塑性软化、损伤,可应用于后续数值计算。
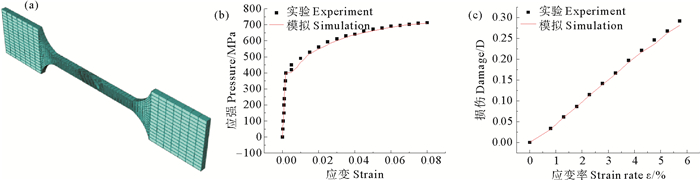
|
图 2 (a) 单轴拉伸模型(b) 应力应变演化曲线(c)损伤应变演化曲线 Fig. 2 (a) Uniaxial tensile model (b) stress-strain evolution curve (c) damage strain evolution curve |
水下传动装置如图 3(a)所示,限位圆盘和转动圆盘构成配合面,外侧限位圆盘固定在轴上,内侧转动圆盘由循环载荷F驱动绕轴转动,驱动力F作用在撑杆上,作用方向如图 3(a)。有限元模型取一侧配合面、轴组成,计算模型尺寸相对工程结构等比例缩小,如图 3(b)所示:两圆盘外半径皆为10 mm、厚度为2 mm,撑杆长度为38 mm,两圆盘配合面间隙为0.6 mm,圆柱轴半径为3 mm、长为30 mm。依分形理论建立三维磨粒模型,如图 4(c)所示,磨粒最大外直径为1 mm。本研究中,循环正弦驱动力,幅值为600 N,周期为0.2 s。依据传动装置实际工作状态观察,磨粒初进入两圆盘间隙,完好附于配合面表面,内侧圆盘在驱动力作用下循环转动而引起磨粒磨损。传动装置处于海洋环境,配合面上腐蚀不可避免,很可能引入新的应力集中,从而影响磨粒和配合面损伤演化过程;另外,传动装置运动与整体水入水过程一致,因此配合面循环转动中还存在高低温变化,无磨粒磨损情况下环境温差对于配合面应力状态影响较小,但是磨粒局部应力集中十分显著,应考虑温度循环的影响。本文中,将对点腐蚀、面腐蚀状态下传动装置磨粒磨损过程进行计算,并引入温度因素,对比研究海洋环境下传动装置小间隙配合面磨粒磨损与传动性能变化规律,具体工况见表 1。

|
图 3 (a) 传动配合面示意图、点蚀(12蚀坑)磨粒(3颗)磨损(b) 模型及(c) 配合面网格 Fig. 3 (a) Schematic diagram of transmission mating surface, pitting (12 pits) abrasive particles (3 pieces) abrasion (b) model and (c) mesh of mating surface |
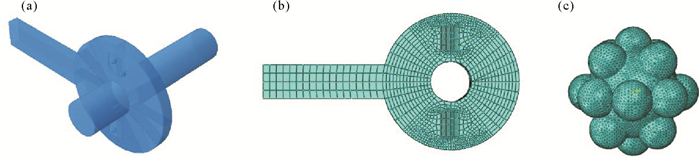
|
图 4 面蚀(2蚀面)磨粒(3颗)磨损(a) 模型,(b) 配合面网格,(c) 分型磨粒模型与网格 Fig. 4 Surface erosion (2 erosion surface) abrasive particles (3) wear (a) model, (b) mating surface mesh and (c) parting abrasive model and mesh |
|
|
表 1 计算工况 Table 1 Calculation conditions |
本文利用ABAQUS求解器对含腐蚀配合面磨粒磨损进行计算,腐蚀坑和面通过Partition功能对模型进行分割,同时对腐蚀周边区域网格细化,保证应力梯度较大区域中单元尺寸足够小,避免网格畸变。选用4节点一阶减缩积分壳单元(S4R),使用线性插值法,允许有限薄膜应变和大旋转角,考虑了剪切变形的影响。在单元几何类型的选择上,常用单元有四边形、三角形等,其中四边形单元为首选,三角形单元虽然具有较好的边界适应性,但计算精度较差,划分的单元数过多,占用计算机内存大,给计算带来不利。以含12点蚀坑和3磨粒配合面磨损为例,边界条件和网格模型如图 3和4所示。本研究中,配合面圆盘网格特征尺寸为0.89 mm,磨粒网格特征尺寸为0.022 mm,圆轴网格特征尺寸为1 mm,以上尺寸可较准确反映结构中应力集中与梯度特征并描述损伤演化。在施加荷载的分析步中,允许配合面绕z轴转动,约束其它方向的运动。采用正弦循环驱动力荷载加载方式,以此模拟配合面五次循环运动过程,磨粒与配合面间采用面面接触,内圆盘与轴承间也采用面面接触,接触面间摩擦因数取0.15,法向定义为“硬接触”即存在法向应力时,接触面接触,当法向应力为零或负值时,接触面分离。材料本构采用前述韧性损伤演化模型,弹性模量223 GPa,泊松比0.3。
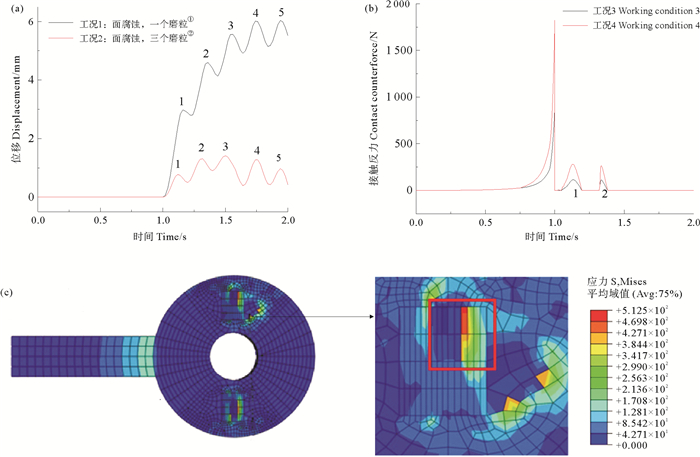
图 5(a)为点蚀情况下配合面驱动力与转动关系,纵轴为传动圆盘转动角度,横轴为传动时间,图中标记数字为传动圆盘转动周数。无腐蚀情况下,随驱动力循环作用,转动圆盘出现永久位移且随循环次数不断增加,配合面间相对位置无法恢复至初始状态,结构传动性能显著下降。考虑点蚀情况,相同载荷过程,点蚀配合面转动幅度远小于无腐蚀的配合面,而且差值随转动过程逐渐增大,即腐蚀显著影响配合面运动,使得传动性能下降。考虑面腐蚀情况,结构磨损和传动性能变化趋势与点腐蚀情况定性一致。根据旋转位移曲线图可得到,无腐蚀情况下一个磨粒工况最大转角为27.22 ℃,三个磨粒工况为6.27 ℃,点腐蚀情况下,一个磨粒工况最大转角为6.25 ℃,三个磨粒工况为3.18 ℃,图 6(a)为面蚀情况下配合面驱动力与转动关系,面蚀情况下,一个磨粒工况最大转角为11.3 ℃,三个磨粒工况最大转角为0.88 ℃。将不同工况下的最大转角总结如表 2。
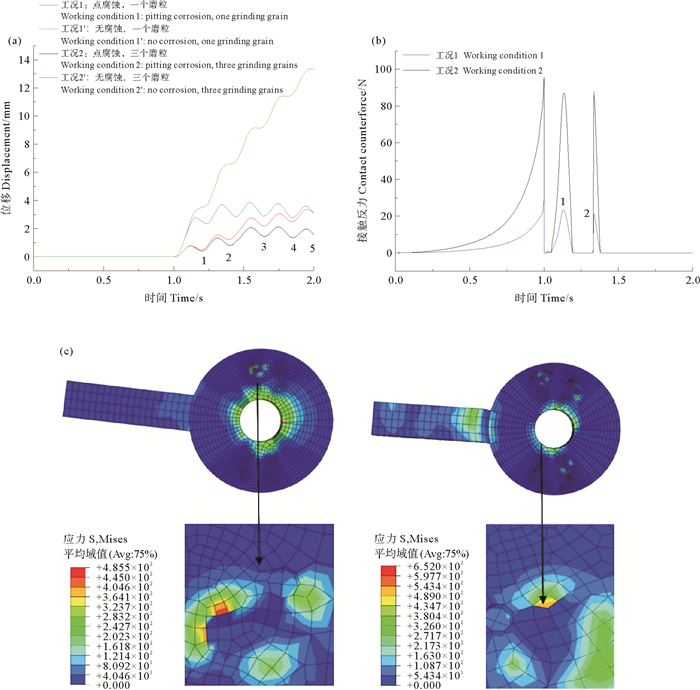
|
图 5 (a) 旋转位移与时间关系、(b)接触力与时间关系及(c)点蚀配合面磨损 Fig. 5 (a) Relationship between rotation displacement and time, (b) relationship between contact force and time and (c) pitting wear on mating surface |
|
(①Working condition 1: surface corrosion, one grinding grain; ②Working condition 2: surface corrosion, three grinding grains) 图 6 (a) 旋转位移与时间关系,(b)接触力与时间关系及(c)面蚀配合面磨损特征 Fig. 6 (a) Relation between rotation displacement and time, (b) relation between contact force and time and (c) wear characteristics of surface corrosion and surface |
|
|
表 2 不同工况下最大转角 Table 2 Maximum corner under different operating conditions |
细观上进一步分析上述现象产生的原因,磨粒与配合面之间的的挤压旋转是一种符合“犁耕”理论的现象,即任何物体想要占有一定的空间,都必须排除以前在这个地方的其他物体。而在上述计算模型中,由于腐蚀及磨损产生了磨粒及配合面产生了孔洞、沟犁[17]现象,磨粒与配合面不断地啮合或分离,而形成一种反复的离合过程。在啮合与分离的过程中,磨粒的某一部分,由于破损或脱落而产生细微破坏[18],这逐渐改变了接触条件,使得配合面的旋转更加困难,同时,磨粒及配合面磨损不断加剧;而且,配合面旋转过程中出现接触变形,使磨损微粒嵌入配合面表面磨损特性如图 5(c)图 6(c)所示,从而产生切削作用,切削的阻力就是磨损阻力,而由接触反力图 5(b)、图 6(b)可见,两类腐蚀情况下磨粒和配合面间接触力远大于无腐蚀情况,这是由于蚀坑的几何奇异性加大了应力三轴度,增大的应力三轴度显著加速损伤演化,磨损情况下点腐蚀的蚀坑间存在应力集中融合趋势,即产生应力集中与损伤条带,加速磨粒与配合面损伤演化,从而使得两者间接触力更快速发展。需要注意,点腐蚀对磨粒磨损的影响小于面腐蚀,即面腐蚀磨损时结构运动性能下降更显著,由模拟结果分析,磨粒进入面腐蚀区域后,在其平面内存在两个方向的完全约束,而点腐蚀仅对磨粒局部产生约束,面腐蚀情况下配合面和磨粒中应力三轴度增大速度和幅值都远大于点腐蚀情况,结构和磨粒塑性破坏速度和程度也就是远大于点腐蚀情况,因此结构传动性能下降更快。
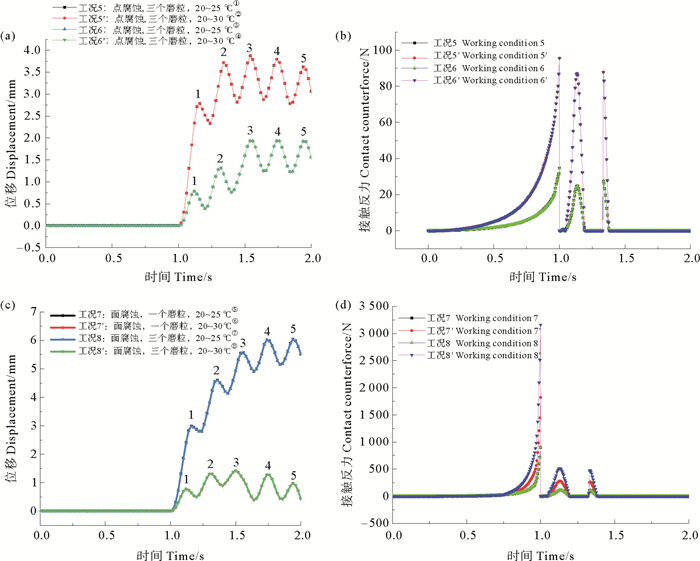
3.2 温度变化时含腐蚀配合面磨粒磨损过程与装置传动性能变化考虑腐蚀及温度同时作用下对磨粒磨损接触模型的影响。以点腐蚀和面蚀模型作为计算模型,分为1个磨粒、3个磨粒2组,温度从20 ℃升高至25 ℃、从20 ℃升高至30 ℃时两种件下的磨损情况,计算结果如图 7。同时考虑腐蚀及温度作用对于配合面的正常工作影响时,相对于仅考虑腐蚀作用对配合面旋转位移的影响,二者在演变过程中有区别,不过最终旋转位移基本一致,出入水导致温度变化相对于腐蚀,对于配合面磨粒磨损影响较小,腐蚀作用应作为工程设计重点关键因素。但是和仅有腐蚀作用的工况相比,增加温度作用时的配合面应力明显增大,这对传动装置使用寿命有一定影响,因此在结构设计及防护方面,温度也是需要考虑的因素。
|
(①Working condition 5: pitting corrosion, one grinding grain, 20~25 ℃; ②Working condition 5′: pitting corrosion, one grinding grain, 20~30 ℃; ③Working condition 6: pitting corrosion, three grinding grains, 20~25 ℃; ④Working condition 6′: pitting corrosion, three grinding grains, 20~30 ℃; ⑤Working condition: surface corrosion, one grinding grain, 20~25 ℃; ⑥Working condition: surface corrosion, one grinding grain, 20~30 ℃; ⑦Working condition: surface corrosion, three grinding grains, 20~25 ℃; ⑧Working condition: surface corrosion, three grinding grains, 20~30℃.) 图 7 (a) 温度变化下点腐蚀旋转位移与时间关系、(b)点腐蚀接触力与时间关系、(c)温度变化下面腐蚀旋转位移与时间关系及(d)面腐蚀接触力与时间关系 Fig. 7 (a) The relationship between the corrosion rotation displacement and time at the point under temperature change, (b) the relationship between the corrosion contact force and time at the point, (c) The relationship between the corrosion rotation displacement and time at the point under temperature change and (d) the relationship between the corrosion contact force and time at the surface |
(1) 不考虑环境因素,传动装置运行中磨粒与配合面受强非比例载荷作用,金属韧性损伤快速演化使磨粒与配合面的形貌产生显著变化,磨粒破碎、配合面局部产生沟犁,传动装置转动数周后啮合力幅值急剧增大而完全约束结构运动,以上结果与工程实际一致。因此,基于细观损伤模型和细宏观统一建模方法,通过ABAQUS有限元软件的二次开发,所构建的小间隙配合面磨粒磨损模拟系统能正确反映传动装置破坏机理并实现预测。
(2) 考虑海洋腐蚀作用,模拟发现腐蚀对磨粒产生局部约束作用,使磨粒与配合面的表面都产生应力奇异性,进一步增强应力三轴度而加速损伤演化,腐蚀存在连通为条带损伤的趋势,传动装置运动能力下降速度较无腐蚀条件更快。
(3) 考虑温度变化作用,模拟发现分形磨粒中不同接触部位温度差异较大,说明在球形分形磨粒磨损模型中,热量积聚较慢而使其中温度分布存在差异,对应最大应力也发生变化,这导致表层材料损伤演化速度加快,传动装置运动能力下降速度较低温条件更快。
| [1] |
杨桂通. 弹塑性力学引论[M]. 北京: 清华大学出版社, 2004. Yang G T. Introduction to Elastoplastic Mechanics[M]. Beijing: Tsinghua University Press, 2004. (  0) 0) |
| [2] |
Moralesespejel G E. Particle damage in hertzian contacts and life ratings of rolling bearings[J]. Tribology Transactions, 2008, 51(4): 428-445. DOI:10.1080/10402000802011752
(  0) 0) |
| [3] |
樊瑜瑾, 杨晓京, 李浙昆, 等. 磨粒磨损中微观接触过程的有限元分析[J]. 机械工程学报, 2005(4): 35-37. Fan Y J, Yang X J, Li Z K, et al. Finite element analysis of micro-contact process in abrasive wear[J]. Chinese Journal of Mechanical Engineering, 2005(4): 35-37. (  0) 0) |
| [4] |
Tallian T E. Prediction of rolling contact fatigue life in contaminated lubricant: Part Ⅱ. Experimental[J]. Journal of Lubrication Technology, 1976, 98(3): 384-392. DOI:10.1115/1.3452865
(  0) 0) |
| [5] |
Tallian T E. Prediction of rolling contact fatigue life in contaminated lubricant: Part Ⅰ. Mathematical model[J]. Journal of Lubrication Technology, 1976, 98(3): 251-383.
(  0) 0) |
| [6] |
张勇强. 干接触磨粒磨损研究[D]. 杭州: 浙江大学, 2018. Zhang Y Q. Study on Dry Contact Abrasive Wear[D]. Hangzhou: Zhejiang University, 2018. (  0) 0) |
| [7] |
张勇强, 汪久根, 陈芳华, 等. 磨粒磨损的磨粒接触热分析[J]. 润滑与密封, 2018, 43(10): 1-5. Zhang Y Q, Wang J G, Chen F H, et al. Contact thermal analysis of abrasive wear[J]. Lubrication and Sealing, 2018, 43(10): 1-5. (  0) 0) |
| [8] |
张勇强, 汪久根, 陈芳华, 等. 磨粒磨损的接触分析[J]. 润滑与密封, 2008, 43(3): 11-16. Zhang Y Q, Wang J G, Chen F H, et al. Contact analysis of abrasive wear[J]. Lubrication & Sealing, 2008, 43(3): 11-16. (  0) 0) |
| [9] |
Barge M, Kermouche G, Gilles P, et al. Experimental and numerical study of the ploughing part of abrasive wear[J]. Wear, 2003, 255(1-6): 30-37. DOI:10.1016/S0043-1648(03)00159-5
(  0) 0) |
| [10] |
李向哲, 许金泉. 一个可区分破坏模式的新应力三轴度参数[J]. 应用力学学报, 2020, 37(3): 921-927, 1381. Li X Z, Xu J Q. A new triaxial stress parameter for distinguishing failure modes[J]. Chinese Journal of Applied Mechanics, 2020, 37(3): 921-927, 1381. (  0) 0) |
| [11] |
肖祥麟. 摩擦学导论[M]. 上海: 同济大学出版社, 1990. Xiao X L. Introduction to Tribology[M]. Shanghai: Tongji University Press, 1990. (  0) 0) |
| [12] |
羊亚平, 王少杰, 冯伟国. 分形与分维[J]. 工科物理, 1996(1): 3-5. Yang Y P, Wang S J, Feng W G. Fractal and fractal dimension[J]. Physics of Engineering, 1996(1): 3-5. (  0) 0) |
| [13] |
吴国清, 张晓峰, 方亮, 等. 两体磨料磨损的三维动态模拟[J]. 摩擦学学报, 2000(5): 360-364. Wu G Q, Zhang X F, Fang L, et al. Three-dimensional dynamic simulation of two-body abrasive wear[J]. Journal of Tribology, 2000(5): 360-364. (  0) 0) |
| [14] |
刘峰璧, 李续娥, 谢友柏. 载荷动态特性对三体磨料磨损过程的影响[J]. 机械设计与研究, 2000(1): 45-46. Liu F B, Li S E, Xie Y B. Influence of dynamic load characteristics on three-body abrasive wear process[J]. Mechanical Design and Research, 2000(1): 45-46. (  0) 0) |
| [15] |
杨晓京, 陈子辰, 樊瑜瑾, 等. 磨粒微观滑动接触过程热效应的有限元分析[J]. 润滑与密封, 2007(8): 1-4. Yang X J, Chen Z C, Fan Y J, et al. Finite element analysis of thermal effect in micro-sliding contact process of abrasive particles[J]. Lubrication Engineering, 2007(8): 1-4. (  0) 0) |
| [16] |
王铁军, 张新平. 低合金结构钢及其焊缝热影响区的韧性损伤演化行为[J]. 应用力学学报, 1995(3): 96-101. Wang T J, Zhang X P. Ductile damage evolution behavior of low alloy structural steel and its weld seam heat affected zone[J]. Journal of Applied Mechanics, 1995(3): 96-101. (  0) 0) |
| [17] |
岑启宏, 孙琨, 方亮, 等. 二体磨料磨损犁沟及脊的三维有限元动态模拟[J]. 摩擦学学报, 2004(3): 249-253. Cen Q H, Sun K, Fang L, et al. Three-dimensional finite element dynamic simulation of furrows and ridges of two-body abrasive wear[J]. Chinese Journal of Tribology, 2004(3): 249-253. (  0) 0) |
| [18] |
岳晓宇. 基于ABAQUS的导轨副磨粒磨损微观过程的有限元研究[D]. 天津: 天津理工大学, 2014. Yue X Y. Finite Element Study on Micro-Process of Wear of Guide Rail Based on ABAQUS[D]. Tianjin: University of Technology, 2014. (  0) 0) |
2. College of Engineering, Ocean University of China, Qingdao 266100, China
 2022, Vol. 52
2022, Vol. 52


