随着仿生学在工程应用上研究的不断发展,人们开始注意到鱼类本身灵活、高效的运动方式,并模仿鱼的外形特征及其运动方式,将其流线型外形特征和运动方式应用到水下机器人的研究中。通过对比传统的螺旋桨推进方式,仿鱼鳍驱动水下机器人推进具有高效率、高机动性、转弯半径小、运动控制灵活与低扰动、低噪声等优点[1],为研制新型仿生机器鱼及水下推进技术提供了新的思路和发展方向。仿生机器鱼的研究工作可分为两个阶段:1990年代以前主要是基础理论方面的研究,对于鱼类推进机理的研究,学者们已经取得了较多的成果。GRAY[2]针对海豚游动进行研究,以能量守恒角度提出海豚游动效率远远超出100%,后人称为“GRAY疑题”。LIGHTHILL将空气动力学的二维机翼理论运用于尾鳍推进的研究,提出了用于分析鲹科鱼类推进模式的“细长体理论”,后进一步又提出了“大摆幅细长体理论”[3-4]。吴耀祖通过研究提出了“二维薄板理论”[5],将鱼看成一个具有弹性的薄板,进一步,又提出了“非定常二维波动板理论”[6],该理论分析了扁平月牙尾鱼的推进及优化方式。2011年FABIEN等将细长体理论推广到三维情况,获得了作用于细长体上的压力表达式和动量表达式[7]。1990年代以后随着机器人技术、驱动装备和新型智能材料等技术的发展给仿生机器鱼的研究提供了强大的技术支持,极大地促进了仿生水下机器人的发展。美国麻省理工学院以蓝鳍金枪鱼为蓝本,研制了世界上第一条真正意义上的仿鱼水下机器人ROBOTUNA。随后以黄鳍金枪鱼为蓝本研制了VCUUV[8]机器鱼,其能够利用涡流来控制实现仿生机器鱼的推进。
随着计算机技术大力发展、相关CFD(Computational Fluid Dynamics)技术的逐渐成熟,出现了使用数值模拟对水下泳动生物运动进行研究分析的方法,研究者使用CFD来仿真鱼体周围的流场和压力场,进而计算出力场,涌现出许多成果[9]。WOLFGANG等[10-11]结合活鱼的实验数据,运用三维面元法分析金枪鱼的游动特征,并研究尾迹中的漩涡干扰和控制。苏玉民和黄胜[12]用三维面元法计算分析了仿生金枪鱼刚性及柔性尾鳍的非定常水动力性能。杨亮[13]利用FLUENT软件的二次开发,采用动网格技术详细计算了具有金枪鱼尾鳍运动规律的机翼在粘性流场中的水动力性能,计算分析了三维尾鳍的非定常水动力性能。马尧和赵宏伟对金枪鱼在海洋环境中的游动进行仿真,着重分析了机器鱼表面压强,湍流动能以及周围流体流速等性能指标[14]。周澍欣, 胡庆松使用fluent将鱼体和鱼鳍整体作为研究对象在流场中进行了受力分析[15]。
金枪鱼具有典型流线型外形,其体形特点适合传感器等的布放。本文以金枪鱼鱼体特征为对象进行分析,将其体形特征进行数学化描述,将其用于仿生机器鱼体的三维建模和网格化,最终在ANSYS(Fluent模块)中进行来流为定常流时鱼体在给定流场下所呈现的力学特征计算,根据结果对比分析流线型鱼体在减阻方面的功能,为仿生机器鱼的优化设计提供支撑。
1 仿生金枪鱼模型鱼的种类繁多,外形更是多种多样,但一般都可分为头部、躯干和尾部三部分。在众多的鱼类中,金枪鱼鱼体的长宽比、躯体厚度、尾部特征等具有较好的比例,适宜进行内部结构设计以放置控制系统、驱动系统和传感器元件等功能装置,故以其为仿生对象进行分析研究。本文根据金枪鱼的体长、体宽、体高、尾鳍等特征,按文献[16]的方法建立仿生金枪鱼的三维模型,如图 1所示。尾鳍形状比率为0.14,建立的模型为在自然状态下处于直线型的金枪鱼。

|
图 1 仿生机器鱼三维模型 Fig. 1 The 3D model of bionic robot fish |
为便于进行数值分析计算,合理的网格划分非常重要。通常流体计算域网格划分一般可将体网格分为结构网格和非结构网格,相对于结构网格,非结构网格虽然生成过程比较复杂,但有极好的适用性,划分效率高,方便划分复杂形体模型,并且能够很好地处理复杂边界的流场计算问题等优点,适用模型中尾鳍等尖端部分的网格划分,故选取非结构网格主体的划分方法。
鱼体长度l=13 cm、最大宽度b=5 cm、最大高度h=6.8 cm,为了避免外流场边界引起边界效应,设定计算域的长度L=50 cm、宽度B=20 cm、高度H=20 cm。并设定鱼体在计算域的中心位置,其中鱼头朝向X轴的正方向,鱼尾鳍相对于鱼体处在Y轴的正方向。
2.2 湍流模型CFD中的湍流模型的引入是解决湍流运动的方程组采用了某种平均而不封闭的问题。数值模拟的关键是湍流模型的选择,在众多的湍流模型中,当前最常用的是基于“雷诺平均N-S(RANS)方程组”的k-ε模型。而k-ε模型又可分为标准的k-ε模型和RNG k-ε模型两种。其中标准的k-ε模型是一种高雷诺数模型,RNG k-ε模型在标准的k-ε模型的基础上增加了一个考虑低雷诺数流动的解析公式并进行了相应的改进,使其在模拟湍流流动中具有更高的精度。本文仿真计算中,由于进口的来流速度较小,仿生机器鱼特征尺寸较小,因此属于低雷诺数范围,采用RNG k-ε模型能够将微分粘性模型加入其中,从而得到更接近理论计算值。
RNG k-ε模型的具体形式为:
| $ \frac{\partial (\rho k)}{\partial t}+\frac{\partial \left( \rho k{{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left( {{\alpha }_{\varepsilon }}{{\mu }_{\text{eff}}}\frac{\partial k}{\partial {{x}_{j}}} \right)+{{G}_{k}}+\rho \varepsilon 。$ | (1) |
| $ \begin{align} & \frac{\partial (\rho \varepsilon )}{\partial t}+\frac{\partial \left( \rho \varepsilon {{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left( {{\alpha }_{\varepsilon }}{{\mu }_{\text{eff}}}\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right)+\frac{\varepsilon }{k}C_{1\varepsilon }^{*}{{G}_{k}}- \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{C}_{2\varepsilon }}\rho \frac{{{\varepsilon }^{2}}}{k} \\ \end{align}。$ | (2) |
| $ {{\mu }_{\text{t}}}={{C}_{2\varepsilon }}\rho \frac{{{\varepsilon }^{2}}}{k}, {{\mu }_{\text{eff}}}=\mu +{{\mu }_{t}}。$ | (3) |
式中:μt为湍动粘度,ε为湍流耗散率,k为湍流动能,ρ为流体密度,Gk是由于平均速度梯度引起的湍动能k的产生项,Gb是由于浮力引起的湍动能k的产生项,C1ε、C2ε为经验系数。计算时各经验常数Cμ=0.084 5,αk=αε=1.39,C1ε=1.42,C2ε=1.68[17]。
2.3 初始条件鱼类游动的环境为自然状态下的湖泊河流,故选择模型为不可压缩流模型,选择压力基求解器(Pressure-Based)。稳态计算,考虑重力的影响,重力加速度为9.81 m/s2;求解方程选择RNG k-ε模型。流体域右侧为速度进口(velocity-inlet)边界条件,左侧为压力出口(pressure-outlet)边界条件,其余为壁面(wall)边界条件。压力速度耦合方式(Pressure-Velocity)采用SIMPLE算法,因模型是使用3D四面体网格,且研究鱼体在流场中的压力为主要部分,压力差值采用二阶迎风格式(Second order upwind)以提高求解后压力结果的精度(见图 2)。
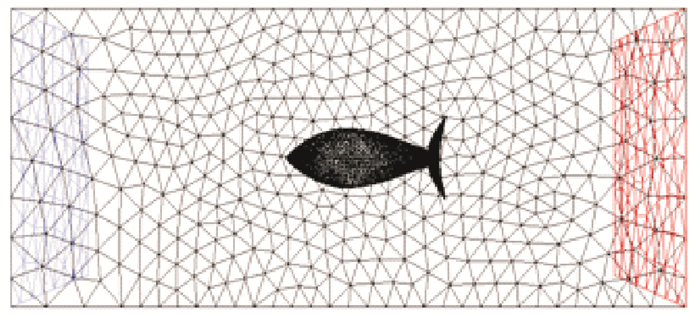
|
图 2 流体域网格划分及边界条件设置 Fig. 2 Set the fluid domain mesh and boundary conditions |
在入口处设置速度为两个鱼身(25 cm/s)及50、100 cm/s的来流。设置收敛标准为,并进行500步的迭代计算。
3 数值结果分析在本仿真计算中所关心的问题为仿生机器鱼体在来流中所呈现的压力分布及游动前进时的阻力情况。
3.1 鱼体在流场中的压力分布图 3、4、5分别是流速为25、50、100 cm/s时仿金枪鱼体在流场中的压力分布云图。从直观的金枪鱼体压力云图中可以看出:鱼体受压云图可大致分为鱼头和鱼身与尾鳍三部分,当来流速度平行于直线机器鱼体长方向时,其头部所受压力最大,而体宽最大处则为负压,尾鳍中间部分受到的是来自两侧的正压,而两个尖端受到的却是负压。随着流速的增大,鱼体头部压力随之增大,负压区域逐渐减小,但体宽最大处仍为负压。综合分析可以看出仿生机器鱼的不同部位在流场中所起到的作用和功能是不同的。在减小某部分运行阻力的设计时,毫无疑问地必须结合鱼体的流线型设计与鱼鳍的形态进行考虑。
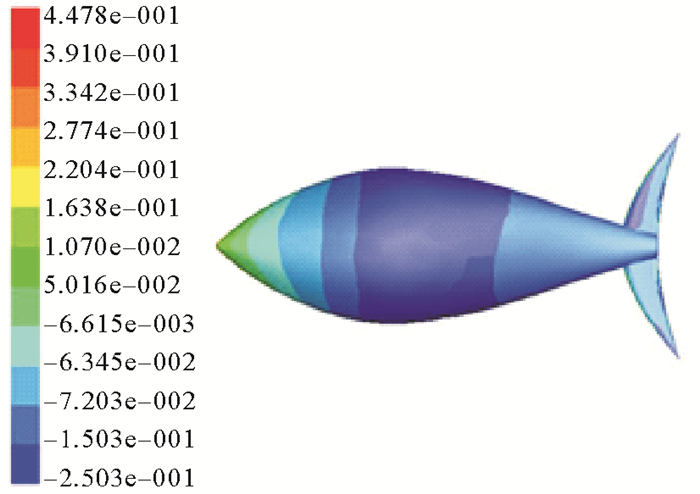
|
图 3 25 cm/s时鱼体压力分布云图 Fig. 3 Pressure distribution nephogram of 25 cm/s |
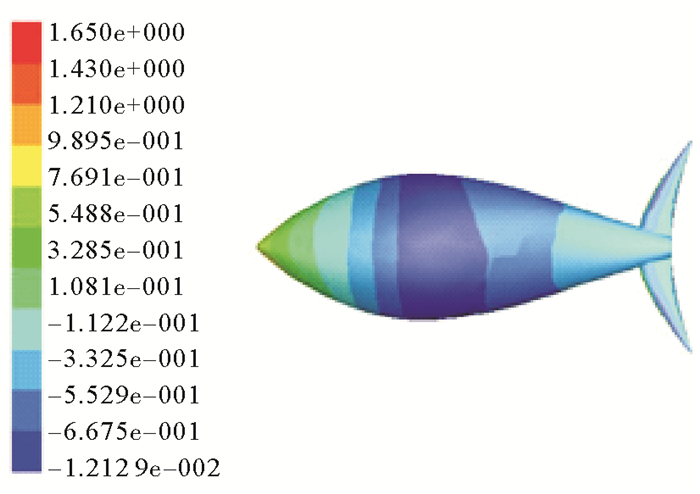
|
图 4 50 cm/s时鱼体压力分布云图 Fig. 4 Pressure distribution nephogram of 50 cm/s |
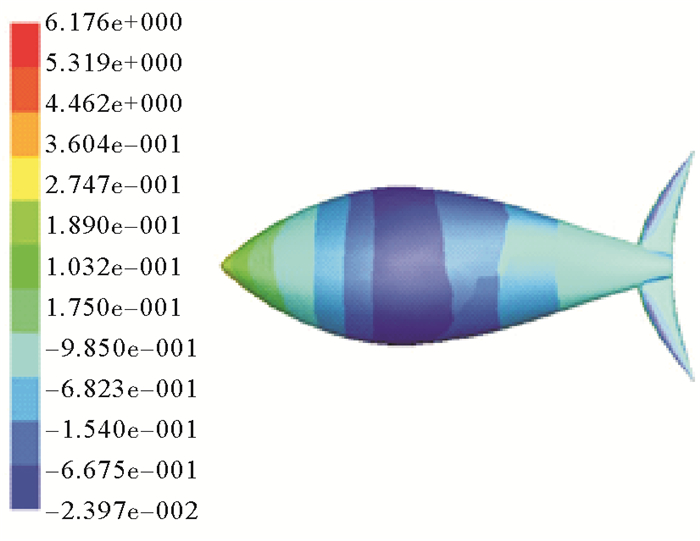
|
图 5 100 cm/s时鱼体压力分布云图 Fig. 5 Pressure distribution nephogram of 100 cm/s |
为分析仿金枪鱼在流场中的特性,选取鱼体所在的中心平面为特征面进行分析。
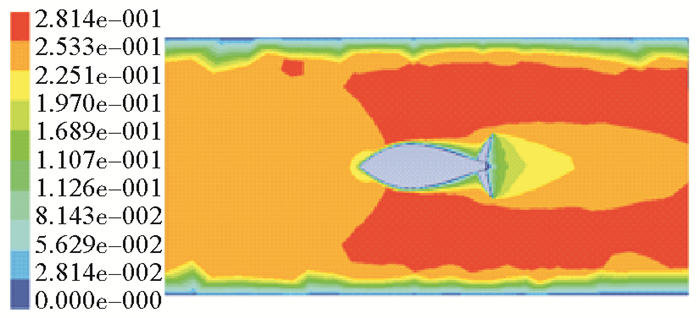
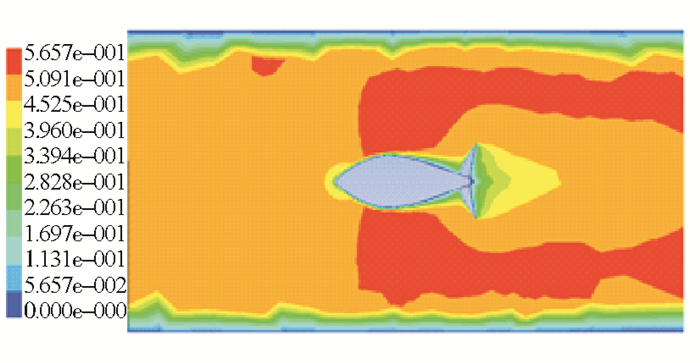
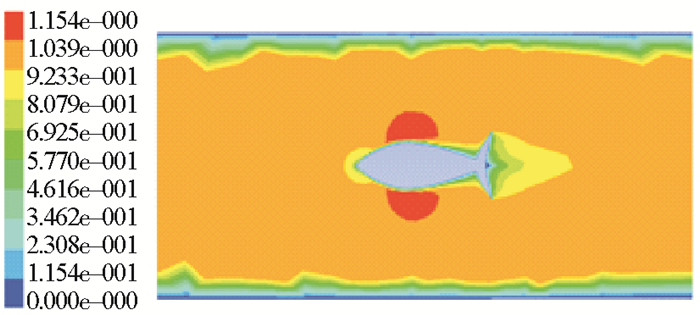
尾迹是一种常见的流动现象,是由各层流体的速度差形成的,当中心的流速比四周的流速小,在流场中的物体下游便形成尾迹。在单个流速场中,远离鱼体的流场没有受到物体的干扰,流场保持稳定;当靠近机器鱼时,水流向两侧分离,速度增加,而尾鳍后流速较小,从而形成尾迹。而从图 6、7、8可以看出,由于紧邻鱼体后部的尾迹区的压力一般是低于周围环境压力的,所以尾迹在刚开始的区域,流体有向中心汇聚的趋势。同时可以看出,水下机器鱼前进时,对远场的影响很小,几乎为零;对近场的影响随着速度的增加而逐渐变小。随着速度的增加,鱼体尾部漩涡也逐渐减小,使得分离点靠近模型的尾部,尾迹区域减小。
|
图 6 25 cm/s时的流速分布云图 Fig. 6 The velocity distribution nephogram of 25 cm/s |
|
图 7 50 cm/s时的流速分布云图 Fig. 7 The velocity distribution nephogram of 50 cm/s |
|
图 8 100 cm/s时流速分布云图 Fig. 8 The velocity distribution nephogram of 100 cm/s |
仿生机器鱼前进时的阻力包括压差阻力、粘性阻力(又称摩擦阻力)和兴波阻力[18]。仿生机器鱼由于在水下航行,当下潜深度超过1/3体长时,其兴波阻力接近于0,而通常情况下仿生机器鱼的水下作业时的深度要远远超过其体长。故可忽略仿生机器鱼产生的兴波阻力,分析时仅考虑压差阻力和粘性阻力。
| $ {{R}_{\text{t}}}=\int{\tau }\cos (\tau , x)\ \text{d}s+\int{p}\cos (p, x)\text{d}s。$ | (4) |
工程中一般定义粘性阻力系数Cf和压差阻力系数Cp它们的定义式如下:
| $ {{C}_{\text{f}}}=\frac{2{{R}_{\text{f}}}}{\rho AU_{\infty }^{2}}, {{C}_{\text{p}}}=\frac{2{{R}_{p}}}{\rho AU_{\infty }^{2}}。$ | (5) |
则有:
| $ {{R}_{\text{t}}}=\frac{1}{2}\rho AU_{\infty }^{2}\left( {{C}_{f}}+{{C}_{p}} \right)=\frac{1}{2}\rho AU_{\infty }^{2}{{C}_{\text{t}}}。$ | (6) |
其中,A为水下机器鱼的湿表面积。
不同航行速度下主体的阻力是不同的,为此在不同速度下进行了阻力分析,Fluent计算结果如表 1所示。
|
|
表 1 仿生机器鱼不同速度时的阻力 Table 1 The drags of robot fish at different speeds |
此外,本文还建立了与金枪鱼模型体长、迎流面积相同的回转体外形水下机器人模型如图 9,对该模型进行流场受力数值计算,与仿生机器鱼的外形阻力进行对比分析。水下机器人模型的阻力计算结果如表 2所示。

|
图 9 回转体型水下机器人 Fig. 9 Rotary type of underwater robot |
|
|
表 2 回转体型水下机器人不同速度时的阻力 Table 2 The drags of robot at different speeds |
将表 1、2中的数据综合分析,可以看出,仿生机器鱼可有效的减小其在水中航行的阻力,提高推进效率。随着航行速度的增大,水下机器人受到的摩擦阻力和粘压阻力都逐渐增大,粘性阻力在总阻力中占有很大份额,总阻力的变化起着决定性影响,压差阻力只占很小一部分,随着航速的提高,在总阻力中所占比例也越小。
此外,机器鱼在来流平行于直线型鱼体的情况下,对受到来流所提供的方向的阻力主要由头部提供,仿生机器鱼鱼体的流线型对鱼体在该情况下所受的阻力以及升力有着重要的影响,在设计仿生鱼体时,在减小运行阻力方面应主要集中在头部以及鱼体的流线型曲面进行优化设计。
4 结语本文依据金枪鱼体形特征参数,建立仿生金枪鱼的三维仿真模型,重点描述了对流场仿真结果影响较大的流线型鱼体和尾鳍部分。采用四面体结构网格对模型进行划分,设置合理的流场边界条件,基于RNG k-ε模型,研究其在特定流场下的力学特征及所受的阻力情况。计算结果表明,头部、尾鳍及鱼体流线型部分对仿生机器鱼的流场特性影响较大。通过与回转体型水下机器人阻力分析对比可得:仿生机器鱼可有效的减小其在水中航行的阻力,提高推进效率。因此,仿生机器鱼体的流线型外形以及尾鳍结构为水下机器人外形结构的优化设计提供了依据。
| [1] |
刘军考, 陈在礼, 陈维山, 等. 水下机器人新型仿鱼鳍推进器[J]. 机器人, 2000, 22(5): 427-432. LIU Jun-Kao, CHEN Zai-Li, CHEN Wei-Shan, et al. A new type of underwater turbine imitating fish-fin for underwater robot[J]. Robot, 2000, 22(5): 427-432. DOI:10.3321/j.issn:1002-0446.2000.05.016 (  0) 0) |
| [2] |
GRAY J. Studies in animal locomotion VI The propulsive power of the dolphin[J]. Journal of Experimental Biology, 1936, 13(5): 192-199.
(  0) 0) |
| [3] |
Lighthill M J. Note on the swimming of slender fish[J]. Journal of Fluid Mech, 1960, 9: 305-317. DOI:10.1017/S0022112060001110
(  0) 0) |
| [4] |
Lighthill M J. Aquatic animal propulsion of high hydromechanical efficiency[J]. Journal of Fluid Mech, 1970, 44: 265-301. DOI:10.1017/S0022112070001830
(  0) 0) |
| [5] |
WU T Y. Swimming of a waving plate[J]. Journal of Fluid Mech, 1961, 10: 321-344. DOI:10.1017/S0022112061000949
(  0) 0) |
| [6] |
WU T Y. Hydrodynamics of swimming propulsion[J]. Journal of Fluid Mech, 1971, 46: 337-355. DOI:10.1017/S0022112071000570
(  0) 0) |
| [7] |
Fabien C, Frederic B, Alban L. Three-dimensional extension of Lighthill's large-amplitude elongated-body theory of fish locomotion[J]. Journal of Fluid Mech, 2011, 674: 196-226. DOI:10.1017/S002211201000649X
(  0) 0) |
| [8] |
Anderson J M, Kerrebrock P A. Thevorticity control unmanned undersea vehicle (VCUUV): An autonomous robot tuna[C]. // Durham, USA: Proceedings of the 11th International Symposium on Unmanned Untethered Submersible Technology, 1999: 63-70.
(  0) 0) |
| [9] |
王安忆, 刘贵杰, 王新宝. 身体/尾鳍推进模式仿生机器鱼研究的进展与分析[J]. 机械工程学报, 2016, 52(17): 137-146. WANG An-Yi, LIU Gui-Jie, WANG Xin-Bao. Development and analysis of body and/or caudal fin biomimetic robot fish[J]. Journal of Mechanical Engineering, 2016, 52(17): 137-146. (  0) 0) |
| [10] |
Wolfgang M J, Anderson J M, Grosenbaugh M A, et al. Near-body flow dynamics in swimming fish[J]. Journal of Experimental Biology,, 2002, 205: 3271-3279.
(  0) 0) |
| [11] |
ZHU Q. Three-dimensional flow structures and vorticity control in fish-like swimming[J]. Journal of Fluid Mech, 2002, 468: 1-28. DOI:10.1017/S002211200200143X
(  0) 0) |
| [12] |
苏玉民, 黄胜, 庞永杰, 等. 仿鱼尾潜器推进系统的水动力分析[J]. 海洋工程, 2002, 20(2): 54-59. SU Yu-Min, HUANG Sheng, PANG Yong-Jie, et al. Hydrodynamic analysis of bionic submersible propulsion system[J]. Oceanographic Engineering, 2002, 20(2): 54-59. DOI:10.3969/j.issn.1005-9865.2002.02.010 (  0) 0) |
| [13] |
杨亮.仿金枪鱼摆动尾鳍的水动力性能与推进机理研究[D].哈尔滨: 哈尔滨工程大学, 2009. YANG Liang. Research on Hydrodynamic Characteristics and Propulsive Mechanism of Oscillating Tuna-tail[D]. Harbin: Harbin Engineering University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10217-1011021192.htm (  0) 0) |
| [14] |
马尧, 赵宏伟. 基于CFD的仿生机器鱼数值仿真分析[J]. 白城师范学院学报, 2014, 28(5): 14-18. MA Yao, ZHAO Hong-Wei. Numerical simulation analysis of biomimetic robotic fish based on CFD[J]. Journal of Baicheng Normal College, 2014, 28(5): 14-18. (  0) 0) |
| [15] |
周澍欣, 胡庆松. 鲤鱼三维建模及流场受力数值计算[J]. 上海海洋大学学报, 2013, 22(6): 854-861. ZHOU Shu-Xin, HU Qing-Song. Carp 3D-modeling and stress calculation in flow field[J]. Journal of Shanghai Ocean University, 2013, 22(6): 854-861. (  0) 0) |
| [16] |
俞经虎, 仿生机器鱼运动分析研究[D].合肥: 中国科学技术大学, 2004. YU Jing-Hu, Kinematic Analysis of Biomimetic Robotic Fish[D]. Hefei: Hefei University of Science and Technology of China, 2004. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y615604 (  0) 0) |
| [17] |
王福军. 计算流体力学分析—CFD软件原理及应用[M]. 北京: 清华大学出版社, 2015: 124-125. WANG Fu-Jun. Computational Fluid Dynamics Analysis-Principles and Applications of CFD Software[M]. Beijing: Tsinghua University Press, 2015: 124-125. (  0) 0) |
| [18] |
柏开祥, 郑伟涛, 王德恂, 等. 基于ITTC-57对于帆板阻力成分的计算与分析[J]. 武汉理工大学学报, 2006, 28(5): 98-101. BAI Kai-Xiang, ZHENG Wei-Tao, WANG De-Xun, et al. Calculating and analyzing of sailboard's resistance component basing on ITTC-57 friction-resistance formula[J]. Journal of Wuhan University of Technolog, 2006, 28(5): 98-101. DOI:10.3321/j.issn:1671-4431.2006.05.029 (  0) 0) |
 2019, Vol. 49
2019, Vol. 49


