2. 中国海洋大学海洋工程重点实验室,山东 青岛 266100
风帆性能对帆船动力性能具有重要影响。柔性风帆形状会随着风况的改变而变化,帆船航行时风帆的真实形状可简称为飞行形状[1],飞行形状影响着风帆周围的气体流动情况和产生的气动力。因此,需要将柔性风帆在不同风况下帆面的压力分布、飞行形状和气动力相互关联,以更准确的评估或者优化风帆性能。
当前针对柔性风帆气动性能的研究取得一定进展。Fossati等[2]对IMS帆船的风帆1∶10比例模型进行风洞试验研究,建立了在逆风条件下柔性风帆性能和飞行形状试验数据库。Fossati等[3]和Bayati等[4]对游艇风帆1∶10比例模型进行风洞试验和数值模拟研究:将薄而轻的压力带黏合在帆面的关键截面上进行压力测量;基于飞行时间(Time of Flight,TOF)技术采用激光扫描仪进行飞行形状测量;将采集的飞行形状作为CFD数值模拟的输入形状,最后将数值模拟结果和试验结果进行比较和验证。Calì等[5-6]在顺风条件下对全尺寸大三角帆进行水上试验和数值模拟研究,采用载荷传感器测气动力,摄影测量法采集飞行形状,通过集成的CFD-CSM对大三角帆进行流固耦合分析,评估了大三角帆在顺风条件下的性能,并同水上试验结果进行对比验证。Bak等[7-9]在逆风条件下基于集成的CFX和LS-DYNA对9.144 m(30英尺)游艇风帆进行双向流固耦合分析,探究了风帆变形和桅杆变形对风帆空气动力学性能的影响。目前已对现代帆船柔性风帆在逆风和顺风条件下的气动性能研究取得重要进展,但针对无人帆船柔性风帆气动性能的研究案例几乎没有,柔性风帆无人帆船脱胎于现代帆船,无人帆船柔性风帆与现代帆船柔性风帆在获能机理、风帆样式和帆布材料等方面并无较大区别,由于无人帆船具有小型化、多功能、自主调帆等特性,要求更精准的风帆气动性能结果,同时为了发挥特定风帆的最佳气动性能,因此无人帆船柔性风帆气动性能的研究面临着机遇和挑战。
构建1.4 m无人帆船主帆初始形状模型和材料模型,用显式有限元分析程序LS-DYNA解决柔性风帆非线性大变形问题,重构变形后的柔性风帆形状。用STAR-CCM+预测柔性风帆空气动力学性能,比较柔性风帆变形形状表面的压力分布、产生的气动力同初始形状表面的差异,讨论柔性风帆变形对空气动力学性能的影响。根据变形风帆气动性能结果绘制CL-CD曲线(极曲线),确定不同航向角(风向角)下的最佳攻角和相应的最大推力系数,对柔性风帆无人帆船横风航行时的控帆策略具有一定的指导价值。
1 数值模拟方法 1.1 流固耦合方法柔性风帆在风载荷下易发生非线性大变形,属于复杂的流固耦合现象,风帆在流体力的作用下变形,风帆变形又影响流体流动,需要反复计算风帆变形和作用在风帆上的流体力直至收敛,即风帆和空气之间发生双向流固耦合。采用非线性有限元程序LS-DYNA的ALE算法和流固耦合技术数值计算柔性风帆的非线性大变形。
空气通过LS-DYNA提供的NULL材料模型结合状态方程来描述。关键字MAT_NULL的输入参数为空气密度,取1.185 kg/m3;多项式状态方程的压力表达式[10]为:
| $ p=C_0+C_1 \mu+C_2 \mu^2+C_3 \mu^3+\left(C_4+C_5 \mu+C_6 \mu^2\right) E 。$ | (1) |
式中μ为动力黏性系数且μ=ρ/ρ0-1。利用γ法则的气体状态方程,线性多项式状态方程参数可以设置为:
| $ \left\{\begin{array}{l} C_0=C_1=C_2=C_3=C_6=0 \\ C_4=C_5=C_{\mathrm{p}} / C_{\mathrm{v}}-1=\gamma-1 \end{array}\right. \text { 。} $ | (2) |
式中γ为比热Cp和Cv之比;定义多项式状态方程的关键字EOS_LINEAR_POLYNOMIAL的输入参数C0=C1=C2=C3=C6=0,C4=C5=0.4,空气单位参考体积上的初始内能E0取2.068×105 J/kg,初始相对体积V0取1。
流体材料采用Euler网格,固体结构采用Lagrange单元来离散,二者之间的耦合通过关键字CONSTRAINED_LAGRANGE_IN_SOLID来实现,该关键字的主要输入参数SLAVE取柔性风帆部分的ID,MASTER取空气部分的ID,在SLAVE段上考虑耦合的积分点个数NQUAD取3。
1.2 流体运动控制风帆周围的湍流使用STAR-CCM+通过求解三维Navier-Stokes(N-S)方程模拟。质量守恒方程、动量守恒方程和能量守恒方程依次[11]为:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial}{\partial t}\left(\rho \boldsymbol{u}_i\right)=0, $ | (3) |
| $ \frac{\partial}{\partial t}\left(\rho \boldsymbol{u}_i\right)+\frac{\partial}{\partial x_j}\left(\rho \boldsymbol{u}_i \boldsymbol{u}_j\right)=-\frac{\partial \boldsymbol{p}}{\partial \boldsymbol{x}_i}+\frac{\partial \tau_{i j}}{\partial x_j}+p \boldsymbol{g}_i+\boldsymbol{F}_i, $ | (4) |
| $ \frac{\partial}{\partial t}\left(\rho h_i\right)+\frac{\partial}{\partial x_i}\left(\rho \boldsymbol{u}_i h\right)=\frac{\partial}{\partial x_i}\left(k+k_i\right) \frac{\partial T}{\partial x_i}+S_h 。$ | (5) |
式中: ρ为流体密度;t为时间;ui、uj分别为流体速度沿i、j方向的分量;xi、xj分别为i、j方向的坐标;p为静压力;τij为应力矢量;gi为i方向的重力分量;Fi为由阻力和能源而引起的其他能源项;h为熵;T为温度;k为分子传导率;ki为由湍流传递而引起的传导率;Sh为定义的体积源。
N-S方程对时间积分获得Reynolds-Averaged Navier-Stokes(RANS)方程以简化复杂的表达式,计算湍流运动,还需要附加湍流方程。用k-ω shear-stress-transport(SST)湍流模型,因为k-ω SST通过考虑湍流中剪切应力的输运以精确计算在逆压梯度下从光滑表面流动分离的开始和数量,所以能够准确模拟风帆周围的气流分离,计算成本比更高阶湍流模型低[12]。
2 柔性风帆模型 2.1 初始形状模型实测的1.4 m无人帆船主帆的关键截面初始拱度通过零厚度NACA 6位数机翼截面a=0.8的中弧线表示,中弧线通过载荷分布线得到,从0至a载荷均匀分布,从a至1载荷线性减小到0,函数表达式[13]为:
| $ \begin{gathered} \frac{y}{c}=\frac{c_{\mathrm{li}}}{2 \pi(a+1)}\left\{\frac{1}{1-a} \cdot\right. \\ {\left[\frac{1}{2}\left(a-\frac{x}{c}\right)^2 \ln \left|a-\frac{x}{c}\right|-\frac{1}{2}\left(1-\frac{x}{c}\right)^2 \ln \left(1-\frac{x}{c}\right)+\right.} \\ \left.\left.\frac{1}{4}\left(1-\frac{x}{c}\right)^2-\frac{1}{4}\left(a-\frac{x}{c}\right)^2\right]-\frac{x}{c} \ln \frac{x}{c}+g-h \frac{x}{c}\right\}, \end{gathered} $ | (6) |
| $ g=\frac{-1}{1-a}\left[a^2\left(\frac{1}{2} \ln a-\frac{1}{4}\right)+\frac{1}{4}\right], $ | (7) |
| $ h=\frac{1}{1-a}\left[\frac{1}{2}(1-a)^2 \ln (1-a)-\frac{1}{4}(1-a)^2\right]+g \text { 。} $ | (8) |
式中: y为中弧线的纵坐标;c为弦长;x为沿弦长方向的距离;a为中弧线类型的标记,a=0.1, 0.2, ……, 0.8, 0.9, 1,此处a=0.8;cli为设计升力系数,此处cli=1。Yoo等[14-15]、Ciortan等[16]和Bak等[7-9]都使用此方法构建游艇风帆初始形状,以进行气动性能计算或者流固耦合研究。
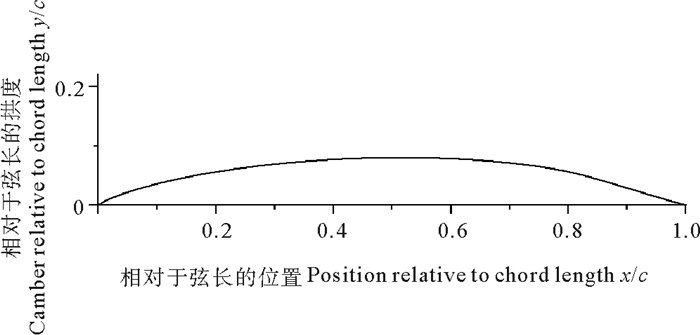
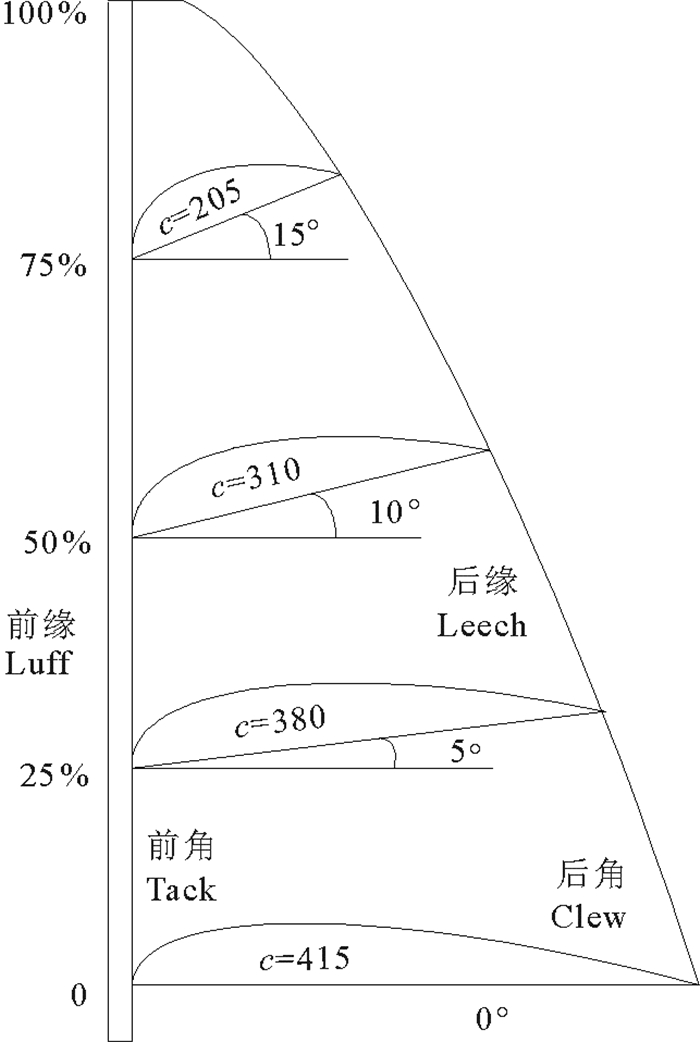
NACA(a=0.8)的中弧线如图 1所示,风帆的5个截面从风帆底边沿竖直向上方向依次命名为0、25%、50%、75%和100%。初始风帆几何参数如表 1所示,几何形状如图 2所示,帆高1.9 m,初始风帆面积0.561 028 m2。
|
图 1 NACA(a=0.8)的中弧线 Fig. 1 NACA(a=0.8) mean line |
|
|
表 1 初始风帆几何参数 Table 1 Geometrical parameters of the initial sail |
|
图 2 初始风帆形状模型 Fig. 2 The shape model of the initial sail |
常用薄织物作为柔性风帆材料,假设材料为均质的各向同性(Isotropic)弹性材料,材料模型采用密度ρ、弹性模量E、泊松比μ和厚度t表征。Kevlar® 49织物的材料特性如表 2所示。
3 柔性风帆变形的流固耦合分析 3.1 流固耦合分析的条件设置采用LS-DYNA进行不同攻角下无人帆船柔性风帆变形的流固耦合数值计算,基于的假设和计算条件:
(1) 无人帆船柔性风帆的初始形状采用图 2所示模型,材料模型采用表 2 Kevlar®49的材料特性近似表示帆布材料。
(2) 风帆的有限元使用壳单元,网格尺寸设置为6 mm;计算域网格尺寸设置为13 mm,除了速度入口外的其他五个面定义为无反射边界面。
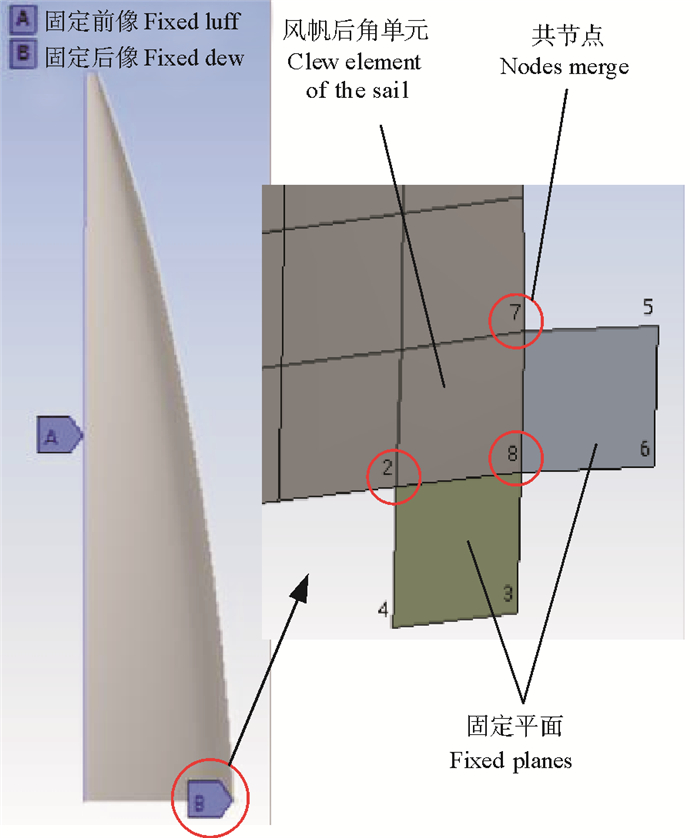
(3) 风帆固定方案。实际上风帆前缘与桅杆相连,后角与横杆末端相连,在数值计算中前缘采用直接固定方案。为了避免计算过程中后角单元失效,单独建2个使用高强度弹性材料的平面与后角单元共节点,然后为这2个平面添加固定约束条件,近似代替风帆的实际固定(见图 3)。
|
图 3 风帆固定方案 Fig. 3 Fixed supports of the sail |
(4) 风速大小设为10 m/s,风帆分别与同纵向风呈10°、20°、22.5°、25°、27.5°、30°、32.5°、35°、37.5°、40°、42.5°、45°、47.5°、50°、60°、70°、80°和90°,探究不同攻角下柔性风帆的变形情况。
(5) 通过后处理输出变形风帆关键截面节点的空间坐标数据,生成变形风帆拱度曲线,然后拱度曲线通过曲面放样来重新构建柔性风帆变形后的形状。
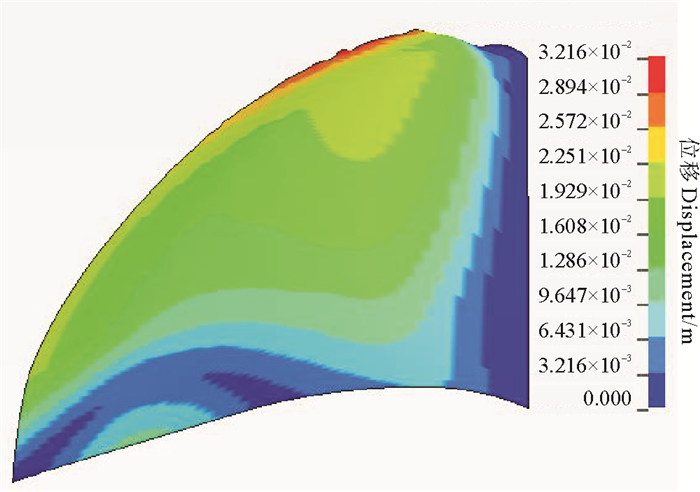
3.2 流固耦合结果分析无人帆船柔性风帆在风载荷作用下的变形情况主要表现为两方面: 一是拱度大小和最大拱度位置变化;二是有效攻角变化。二者决定了变形风帆形状,进而影响风帆周围的气流情况和产生的气动力。图 4显示了20°攻角下柔性风帆的变形位移云图,图 5显示了20°攻角下变形风帆和初始风帆的拱度曲线,结果表明:对5%帆高处的帆面(较低),靠近前缘的帆面拱度向背风侧增大,靠近后缘的帆面拱度向迎风侧减小,最大拱度位置向前缘附近移动;25%~50%帆高处的帆面拱度向背风侧增大,最大拱度位置都向后缘附近移动;对于75%帆高处的帆面(较高),拱度曲线向背风侧变得扁平; 整面风帆的有效攻角减小,且有效攻角减小程度随着距离风帆底部的高度增加而增大。
|
图 4 20°攻角下风帆变形位移云图 Fig. 4 Deformed displacement contour of sail at 20°attack angle |
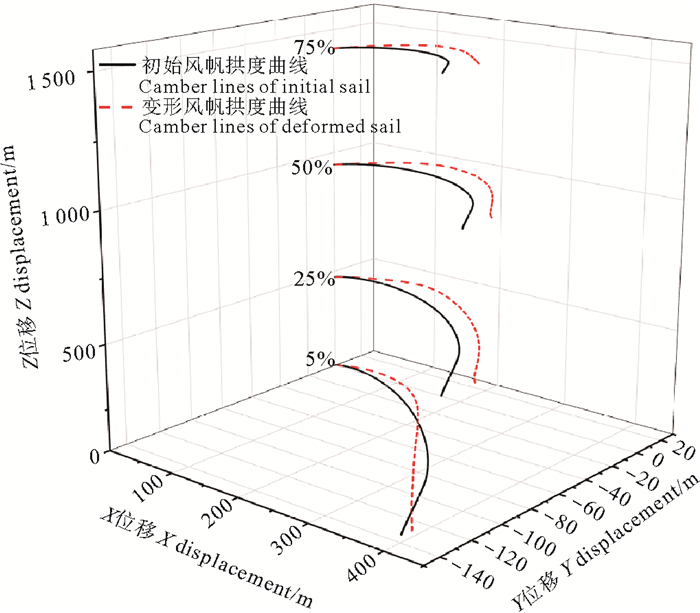
|
图 5 20°攻角下变形风帆与初始风帆拱度曲线 Fig. 5 Comparison of the camber lines for the initial and deformed sails at 20° attack angle |
表 3显示了柔性风帆在不同攻角下的变形形状的面积与初始形状的面积对比,结果表明变形风帆的面积同初始风帆的面积差异率都在0.1%以下,因此柔性风帆面积变化很小,材料在风载荷下自身的拉伸对变形的影响可以忽略不计。
|
|
表 3 不同攻角下的变形风帆与初始风帆面积比较 Table 3 Comparisons of surface areas for initial sail and deformed sails of different attack angles |
图 6显示了柔性风帆在20°、30°、40°、50°和60°攻角下变形风帆4个关键截面的拱度曲线同初始风帆的比较,结果表明:对于5%帆高处的帆面(较低),靠近前缘的帆面拱度向背风侧增大,拱度增大程度随着攻角增大而减小,最大拱度位置随着攻角减小距离前缘更近,而靠近后缘的帆面拱度向迎风侧减小,拱度减小程度随着攻角增大而减小;对于25%~50%帆高处的帆面,帆面拱度增大,拱度增大程度随着攻角增大而减小; 对于75%帆高的帆面(较高),拱度曲线随着攻角减小而更扁平;整面风帆的有效攻角减小,有效攻角减小程度随着攻角增大而减小。
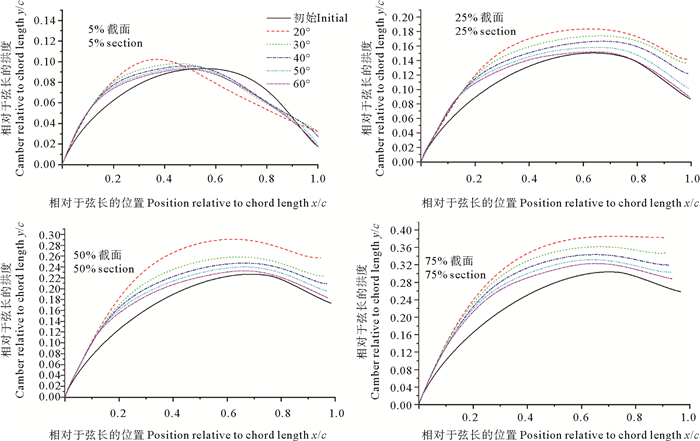
|
图 6 不同攻角下变形风帆与初始风帆拱度曲线比较 Fig. 6 Comparisons of the camber lines for initial sail and deformed sails of different attack angles |
采用STAR CCM+在相同条件下对不同攻角的变形风帆和初始风帆进行流体运动仿真,基于以下假设和计算条件进行气动性能的数值计算:
(1) 风速大小为10 m/s,风帆分别同纵向风呈10°、20°、22.5°、25°、27.5°、30°、32.5°、35°、37.5°、40°、42.5°、45°、47.5°、50°、60°、70°、80°和90°。
(2) 视风帆为计算域内部的无厚度面。为了更清楚的揭示变形对风帆性能的影响,以50%帆高处的截面为界限,分别探讨较低帆面、较高帆面和整个帆面的变形对气动性能变化的影响。
(3) 采用多面体网格。为了提高数值计算精度,加密风帆周围的网格和设置风帆边界层网格。
(4) 物理模型采用RANS方程和k-ω SST湍流模型。
4.2 性能计算结果分析图 7显示了20°攻角下变形风帆和初始风帆的帆面压力分布云图,在迎风侧,变形风帆前缘附近的正压力范围向较低帆面扩大。图 8显示了20°攻角下变形风帆和初始风帆的5%、25%、50%和75%帆高处截面沿弦向的压力分布情况,由图 8可知背风一侧的吸力面的负压力大于迎风一侧的压力面的正压力,两压力面的压差产生力,风帆气动力的主要贡献来自背风一侧的吸力面。同初始风帆相比较,在5%帆高处截面,x/c在0.1~0.65的范围内变形风帆的正压力和负压力增大,x/c在0.65~0.9的范围内变形风帆的正压力和负压力减小,因此5%帆高处截面的拱度曲线靠近前缘部分的拱度向背风侧增大,靠近后缘部分的拱度向迎风侧减小;在25%和50%帆高处的截面,x/c在0.15~0.8的范围内,变形风帆的正压力和负压力都增大,因此25%和50%帆高处截面的拱度向背风侧增大;在75%帆高处的截面,变形风帆的正、负压力的差值显著减小,因此拱度曲线向背风侧变得扁平。

|
图 7 20°攻角下变形风帆和初始风帆迎风侧和背风侧的压力分布云图 Fig. 7 Pressure distribution on both windward and leeward sides of the initial and deformed sails at 20° attack angle |
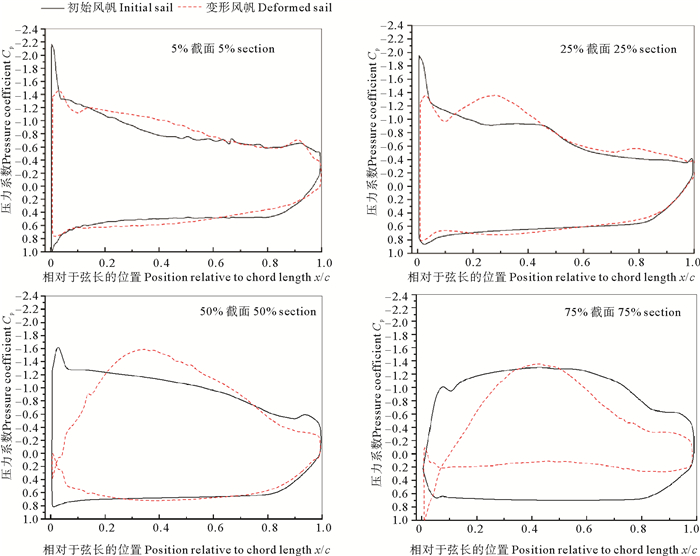
|
图 8 20°攻角下变形风帆和初始风帆的关键截面沿弦向的压力系数值比较 Fig. 8 Comparisons of the pressure coefficient CP over along chord length on sections for the initial and deformed sails at 20° attack angle |
柔性风帆拱度变化和有效攻角变化对产生的气动力具有重要影响。为了更清楚的说明柔性风帆变形对气动性能的影响,以50%帆高处的截面为界限,分别比较较低帆面、较高帆面和整个帆面的变形风帆同相应初始风帆的气动力变化。图 9显示了变形风帆与初始风帆在不同攻角下的升、阻力系数比较,从30°攻角开始,变形风帆较低帆面的升力系数大于初始风帆较低帆面的升力系数;从47.5°攻角开始,变形风帆较高帆面的升力系数大于初始风帆较高帆面的升力系数;从40°攻角开始,对于整个风帆,变形风帆的升力系数大于初始风帆的升力系数。经分析主要原因是当拱度增大带来的升力增大效应强于有效攻角减小带来的升力减小效应时,升力总体上为增大;较低帆面受风面积较大,是产生升力的主要部分。显然,变形风帆的升力系数随着攻角的变化趋势更为合理,且升、阻比初始风帆大。
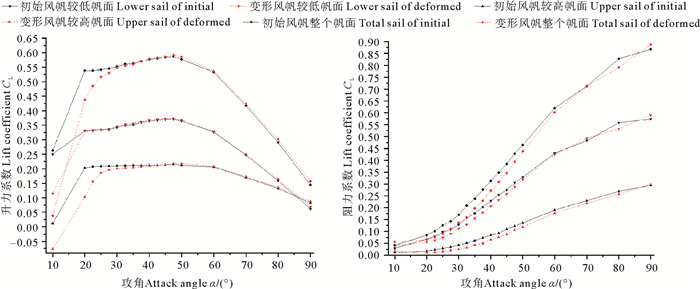
|
图 9 变形风帆和初始风帆在不同攻角下的升、阻力系数比较 Fig. 9 Lift and drag coefficients of the initial and the deformed sails at different attack angles |
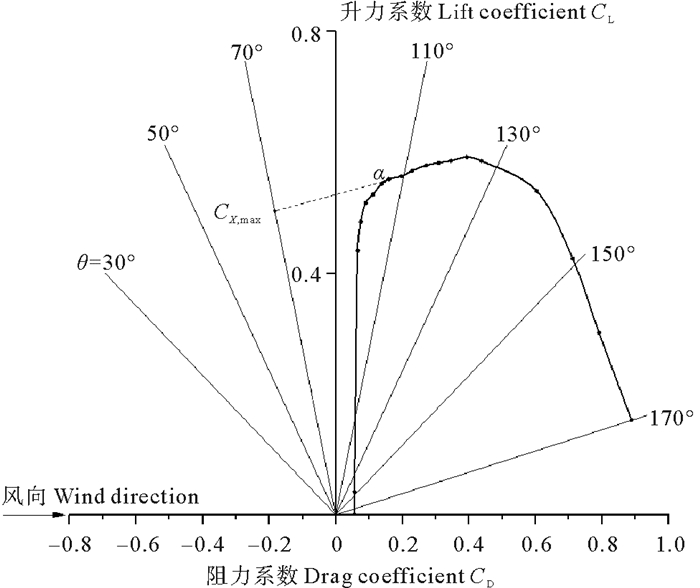
根据变形风帆的气动性能结果绘制CL-CD曲线,如图 10所示。在不考虑无人帆船发生偏航的情况下,相对风向角等于航向角θ,根据极曲线可以找到每一航向角θ下能获得最大推力系数的最佳攻角α,即对航向线作垂线并与极曲线相切的点[17]。因此得到该1.4 m无人帆船主帆在不同航向角下的最佳攻角、最大推力系数以及最大推力系数对应的横向力系数,如表 4所示。而航向角小于30°(逆风航行)和航向角大于150°(顺风航行)时通过该极曲线找不到最佳攻角(见表 4),因此该结果适用于优化柔性风帆无人帆船横风航行时的控帆策略, 对于无人帆船逆风航行和顺风航行时的控帆策略研究需要另外考虑。
|
图 10 变形风帆的极曲线 Fig. 10 The polar curve of the deformed sail |
|
|
表 4 不同航向角下的最佳攻角和最大推力系数 Table 4 The optimal attack angles and maximum thrust coefficients at different heading angles |
采用机翼截面理论构建1.4 m无人帆船主帆的初始形状模型,采用Kevlar®49近似替代柔性风帆的帆布材料,基于非线性有限元程序LS-DYNA的ALE算法和流固耦合技术数值计算柔性风帆在风速10 m/s下、攻角在10°~90°下的非线性大变形问题,处理变形风帆关键截面节点的空间坐标数据重新构建变形风帆的形状模型。通过变形风帆同初始风帆相比较发现:
(1) 柔性风帆在风载荷下的变形情况主要表现为拱度变化和有效攻角变化。
(2) 面积差异率在0.1%以下,柔性风帆材料自身的拉伸作用对拱度的影响可以忽略不计。
(3) 拱度和有效攻角的变化情况在柔性风帆的不同截面、不同攻角下均表现得不一样。
基于STAR CCM+的RANS方程和k-ω SST湍流模型在相同条件下对不同攻角下的变形风帆和初始风帆进行流体运动仿真。将变形风帆同初始风帆相比较可知:
(1) 风帆的帆面压力分布变化同风帆变形结果相互关联。
(2) 变形风帆的较低帆面受风面积大是产生气动力的主要部分。当拱度增大带来的升力增大效应强于有效攻角减小带来的升力减小效应时,升力总体上为增大。
(3) 变形风帆的升力系数随着攻角的变化趋势更为合理,且升阻比较大。绘制变形风帆的极曲线,整理出在不同航向角下的最佳攻角和最大推力系数,适用于优化柔性风帆无人帆船横风航行时的控帆策略。
| [1] |
Deparday J, Bot P, Hauville F, et al. Full-scale flying shape measurement of offwind yacht sails with photogrammetry[J]. Ocean Engineering, 2016, 127(15): 135-143. (  0) 0) |
| [2] |
Fossati F V, Muggiasca S, Martina F. Experimental database of sails performance and flying shapes in upwind conditions[C]//International Conference on Innovation in High Performance Sailing Yachts (INNOVSAIL08), 2008: 99-114.
(  0) 0) |
| [3] |
Fossati F, Bayati I, Muggiasca S, et al. Pressure measurements on yacht sails: Development of a new system for wind tunnel and full scale testing[J]. Journal of Sailing Technology, 2017, 2(1): 1-33. (  0) 0) |
| [4] |
Bayati I, Muggiasca S, Vandone A. Experimental and numerical wind tunnel investigation of the aerodynamics of upwind soft sails[J]. Ocean Engineering, 2019, 182: 395-411. DOI:10.1016/j.oceaneng.2019.04.037 (  0) 0) |
| [5] |
Calì M, Speranza D, Martorelli M. Dynamic spinnaker performance through digital photogrammetry, numerical analysis and experimental tests[M]// Sequenzia G, Rizzuti S, Martorelli M, et al. Advances on Mechanics, Design Engineering and Manufacturing. Cham, Switzerland: Springer, 2017: 585-595.
(  0) 0) |
| [6] |
Calì M, Oliveri S M, Cella U, et al. Mechanical characterization and modeling of downwind sailcloth in fluid-structure interaction analysis[J]. Ocean Engineering, 2018, 165: 488-504. DOI:10.1016/j.oceaneng.2018.07.011 (  0) 0) |
| [7] |
Bak S, Yoo J, Song C Y. Fluid-structure interaction analysis of deformation of sail of 30-foot yacht[J]. International Journal of Naval Architecture and Ocean Engineering, 2013, 5(2): 263-276. DOI:10.2478/IJNAOE-2013-0131 (  0) 0) |
| [8] |
Bak S, Yoo J. FSI Simulation of the sail performance considering standing rig deformation[J]. Journal of the Society of Naval Architects of Korea, 2018, 55(5): 421-430. DOI:10.3744/SNAK.2018.55.5.421 (  0) 0) |
| [9] |
Bak S, Yoo J. FSI analysis on the sail performance of a yacht with rig deformation[J]. International Journal of Naval Architecture and Ocean Engineering, 2019, 11(2): 648-661. DOI:10.1016/j.ijnaoe.2019.02.003 (  0) 0) |
| [10] |
熊令芳, 胡凡金. ANSYS LS-DYNA非线性动力分析方法与工程应用[M]. 北京: 中国铁道出版社, 2016: 211-224. Xiong L F, Hu F J. ANSYS LS-DYNA Nonlinear Dynamic Analysis Method and Engineering Application[M]. Beijing: China Railway Press, 2016: 211-224. (  0) 0) |
| [11] |
李明, 刘楠. STAR-CCM+11.0与流场计算[M]. 北京: 机械工业出版社, 2017: 6-9. Li M, Liu N. STAR-CCM+11.0 and Flow Field Calculation[M]. Beijing: Mechanical Industry Press, 2017: 6-9. (  0) 0) |
| [12] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 (  0) 0) |
| [13] |
Abbott I H, Von Doenhoff A E. Theory of Wing Sections: Including a Summary of Airfoil Data[M]. Chicago: Courier Corporation, 2012: 73-74.
(  0) 0) |
| [14] |
Yoo J H, Park I R, Jin K, et al. Calculations on the interactions between main and jib sails[J]. Journal of the Society of Naval Architects of Korea, 2005, 42(1): 19-31. (  0) 0) |
| [15] |
Yoo J, Kim H T. Computational and experimental study on performance of sails of a yacht[J]. Ocean Engineering, 2006, 33(10): 1322-1342. DOI:10.1016/j.oceaneng.2005.08.008 (  0) 0) |
| [16] |
Ciortan C, Soares C G. Computational study of sail performance in upwind condition[J]. Ocean Engineering, 2007, 34(16): 2198-2206. DOI:10.1016/j.oceaneng.2007.04.005 (  0) 0) |
| [17] |
王献孚. 船用翼理论[M]. 北京: 国防工业出版社, 1998: 195-198. Wang X F. Ship Wing Theory[M]. Beijing: National Defense Industry Press, 1998: 195-198. (  0) 0) |
2. Qingdao Municipal Key Laboratory of Ocean Renewable Energy, Ocean University of China, Qingdao 266100, China
 2023, Vol. 53
2023, Vol. 53


