2. 青岛市海洋可再生能源重点实验室,山东 青岛 266100
潮流能水轮机的实际工作流场是复杂多变的,水轮机时常处于变流速的流动中,因此潮流流经水轮机叶片时流动状态是不稳定的[1]。在大攻角来流工况下,或者当来流速度接近或超过设计流速时,潮流能水轮机叶片边界层会发生流动分离现象,流动分离不仅会增大叶片阻力和降低潮流能水轮机获能效率,甚至会导致叶片失速破坏[2]。因此研究流动分离现象对叶片水动力特性的影响具有重要意义。涡流发生器(VGs: Vortex Generators)作为一种有效的流动控制方法之一,已被成功应用于改善风电叶片的气动特性[3]。
目前,针对涡流发生器的研究主要集中在飞机机翼和风机叶片领域。涡流发生器的几何外形在流场中产生类似飞机机翼尖部的“翼尖涡”,“翼尖涡”通过旋转将边界层外部高速流体能量带入到边界层内增加了边界层克服逆压梯度的能力,延后了流动边界层的分离点,涡流发生器增加了叶片运行工况内的最大升力系数,提高了升阻比,进而提高获能效率[4]。
涡流发生器技术最早由美国联合飞机公司的Bmyne和Taylor等[5]在1947年提出并首次用于机翼上。Gao等[6]研究了涡流发生器对翼型气动性能的影响,以及通过对涡流发生器尾迹区流场的分析,进一步揭示了尾迹区的流场特征。张进等[7]研究了安装在超临界翼型上的微型涡流发生器四种高度和安装位置对绕该翼型的流动影响。在潮流能水轮机领域,袁鹏等[1]通过对潮流能水轮机叶片进行优化来改善叶片的流动分离特性,可以使边界层的转捩点延后,但不能完全解决这一问题。因此本文提出将涡流发生器应用于潮流能水轮机领域,来改善叶片流动分离的现象。
涡流发生器控制流动分离的效果与其自身尺寸参数、涡流发生器对之间的水平安装间距、弦向位置参数、安装角等都有关系,本文研究对象为NACA4418翼型,研究三角形VGs长度、高度、涡流发生器对之间的间距对翼型水动力性能的影响。
1 数值模拟方法 1.1 控制方程本文所采用的计算软件STAR-CCM+为网格适应性、计算稳定性和收敛性方面较好的CFD软件之一[8]。
将翼型绕流问题看作是不可压缩流动问题,本文控制方程选用三维不可压缩Navier-Stokes方程和连续性方程,湍流模型选择耦合了转捩模型Gamma-ReTheta的SST k-ω湍流模型。赵振宙等[9]采用了耦合转捩模型的SST k-ω湍流模型对安装有涡流发生器的叶片微段进行了三维计算,研究结果表明加入转捩模型的计算结果要更加接近实验结果,因此本文中的湍流模型也选择耦合转捩模型。
三维不可压缩Navier-Stokes方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{u_x}}}{{{\rm{d}}t}} = fx - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + v\left( {\frac{{{\partial ^2}{u_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_x}}}{{\partial {z^2}}}} \right)}\\ {\frac{{{\rm{d}}{u_y}}}{{{{\rm{d}}_t}}} = fy - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + v\left( {\frac{{{\partial ^2}{u_y}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_y}}}{{\partial {z^2}}}} \right)}。\\ {\frac{{{\rm{d}}{u_z}}}{{{\rm{d}}t}} = fz - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + v\left( {\frac{{{\partial ^2}{u_z}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_z}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_z}}}{{\partial {z^2}}}} \right)} \end{array}} \right. $ | (1) |
质量守恒原理的流体力学表达式-连续性方程:
| $ \frac{{\partial \left( {\rho {v_x}} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho {v_y}} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho {v_z}} \right)}}{{\partial z}} = 0。$ | (2) |
式中: ρ为流体密度(kg/m3);t为时间(s);ux、uy、uz为x、y、z方向上的速度分量(m/s);p为压力(Pa)。
1.2 转捩模型γ-
(1) 无量纲的间歇因子γ输运方程的守恒形式为:
| $ \frac{{\partial \left( {\rho \gamma } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \gamma {u_j}} \right)}}{{\partial \left( {{x_j}} \right)}} = \frac{1}{{Re}}\cdot\frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _\gamma }{\mu _t}} \right)\frac{{\partial \gamma }}{{\partial {x_j}}}} \right] + {P_\gamma } - {E_\gamma }。$ | (3) |
式中Pγ的表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_\gamma } = {c_{a1}}{F_{{\rm{length}}}}\rho S{{\left( {\gamma {F_{{\rm{onset}}}}} \right)}^{{c_a}}}\left( {1 - {c_{e1}}\gamma } \right)}\\ {{F_{{\rm{onset}}}} = {\rm{max}}\left( {0, {F_{{\rm{onset}}\;}}_{{\rm{2}}} - {F_{{\rm{onset}}\;}}_3} \right)}\\ {{F_{{\rm{onset2}}}} = {\rm{min}}\left( {2.0, {\rm{max}}\left( {{F_{{\rm{onset1}}}}, F_{{\rm{onset1}}}^{\rm{4}}} \right)} \right)}\\ {{F_{{\rm{onset1}}}} = R{e_v}/\left( {2.193R{e_{\theta c}}} \right)}。\\ {R{e_v} = {R_\theta }\rho {y^2}S/\mu }\\ {{F_{{\rm{onset3}}}} = {\rm{max}}\left( {0, 1.0 - {{\left( {\frac{{{R_T}}}{{2.5}}} \right)}^3}} \right)} \end{array}} \right. $ | (4) |
Eγ的表达式为:
| $ \left\{ {\begin{array}{*{20}{c}} {{E_\gamma } = {c_{a2}}{F_{{\rm{turb}}}}\rho \mathit{\Omega} \gamma \left( {{c_{e2}}\gamma - 1} \right)}\\ {{F_{{\rm{turb}}}} = {\rm{exp}}\left( { - {{\left( {{R_T}/4} \right)}^4}} \right)}。\\ {{R_{\rm{T}}} = \rho \kappa /\mu \omega } \end{array}} \right. $ | (5) |
式中:k为湍动能(J);w为湍动能的散耗率;uj为速度(m/s);xj为坐标值;Re为雷诺数;S—应变率的模;Flength为转捩区长度(m);Reθc为边界层内间歇因子开始增加处的动量厚度雷诺数;RT为粘性比;Reν为涡量雷诺数;经验常数:ce1=1.0,ca1=2.0,ce2=50,ca2=0.06,σf=1.0。
(2)
| $ \begin{array}{l} \frac{{\partial \left( {\rho \tilde R{e_{\theta t}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \tilde R{e_{\theta t}}{U_j}} \right)}}{{\partial {x_j}}} = \\ \frac{{\partial \gamma }}{{Re\partial {x_j}}}\left[ {{\sigma _{\theta t}}\left( {\mu + {\mu _t}} \right)\frac{{\partial \tilde R{e_{\theta t}}}}{{\partial {x_j}}}} \right] + {P_{\theta t}}。\end{array} $ | (6) |
式中:
式中参数Pθt的表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{\theta t}} = {c_{\theta t}}\rho \left( {R{e_{\theta t}} - \tilde R{e_{\theta t}}} \right)\left( {1.0 - {F_{\theta t}}} \right)/t}\\ {t = \frac{1}{{Re}}\cdot\frac{{500\mu }}{{\rho {u^2}}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;。\end{array}} \right. $ | (7) |
参数δ、δBL和θBL的表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {\delta = \frac{{50\mathit{\Omega }y}}{U}\cdot{\delta _{BL}}}\\ {{\delta _{BL}} = \frac{{15}}{2}{\theta _{BL}}}。\\ {{\theta _{BL}} = \frac{1}{{Re}}\cdot\frac{{\mu \tilde R{e_{\theta t}}}}{{\rho U}}} \end{array}} \right. $ | (8) |
参数Fθt、Fwake的表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{\theta t}} = {\rm{min}}\left\{ {1.0, {\rm{max}}\left[ {{F_{{\rm{wake}}}}\cdot{e^{ - \left( {y/\delta } \right)}}, 1.0\left( {\frac{{\gamma - 1/{c_{\theta 2}}}}{{1 - 1/{c_{\theta 2}}}}} \right)} \right]} \right\}}\\ {{F_{{\rm{wake}}}} = {\rm{exp}}\left( {{{\left( {\frac{{R{e_\omega }}}{{{{10}^5}}}} \right)}^2}} \right)}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;。\end{array}} \right. $ | (9) |
其中Reω=ρωy2/μ。
根据tomac[12]经验关系式可求出边界层内间歇因子开始增加处的动量厚度雷诺数Reθc以及转捩区长度Flength:
| $ \begin{array}{l} R{e_{\theta c}} = {\rm{min}}\left\{ {0.993\tilde R{e_{\theta t}}, 0.322\tilde R{e_{\theta t}} + \frac{{105{\rm{ }}900}}{{150\sqrt {6.283} }}\cdot} \right.\\ \left. {\left\{ {{\rm{exp}}\left[ { - \frac{1}{2}{{\left( {\frac{{\tilde R{e_{\theta t}} - 560}}{{150}}} \right)}^2}} \right] + {\rm{exp}}\left[ { - \frac{1}{2}{{\left( {\frac{{\tilde R{e_{\theta t}}168}}{{150}}} \right)}^2}} \right]} \right\}} \right\}。\end{array} $ | (10) |
| $ \begin{array}{l} {F_{{\rm{length}}}} = 0.162 + 93.3{\rm{exp}}\left( { - \frac{{\tilde Re_{\theta t}^2}}{{49\;153}}} \right) + \\ \frac{{50}}{{260\sqrt {6.283} }}{\rm{exp}}\left[ { - \frac{1}{2}{{\left( {\frac{{R{e_{\theta t}} - 520}}{{260}}} \right)}^2}} \right]。\end{array} $ | (11) |
本文使用STAR-CCM+三维计算软件,物理模型选用稳态、恒定密度、分离流模型,求解器选用分割法,对翼型流场的N-S方程和连续性方程进行数值求解。
2 研究对象 2.1 翼型选择本文计算采用了NACA4418翼型,该翼型具有较高的升力系数、较小的阻力系数和低扭矩等特性,获能效率较高,在潮流能水轮机中得到了广泛的运用[13]。研究对象为该翼型的直翼段,其长度为105 mm,弦长为600 mm。
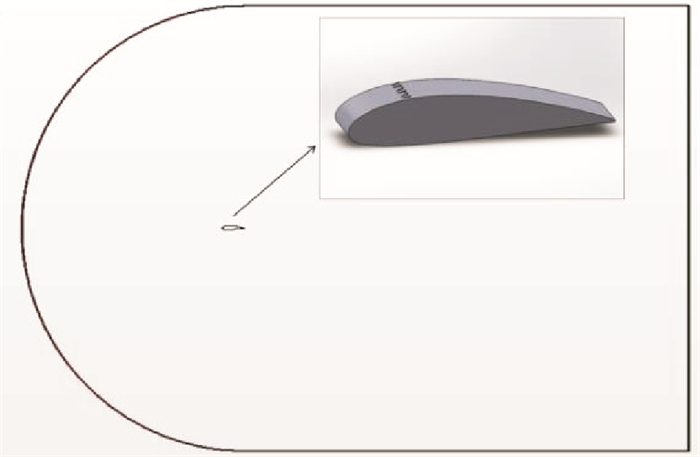
流场图如图 1所示,翼型前缘距离计算域入口15倍弦长,后缘距离出口20倍弦长,翼型距上下边界分别为15倍弦长,放大图中显示了带涡流发生器翼型的三维结构。
|
图 1 计算域流场图 Fig. 1 Flow field diagram |
本文使用STAR-CCM+软件对三维直翼进行网格划分及边界条件设定等前处理。网格为多面体网格,多面体网格采用二元化格式将四面体组合成多面体,是具有不规则数量面的多边形单元,在流体分析方面多面体网格比四面体网格更具有优越性。边界条件设定左侧半圆为速度入口边界条件,入口速度取1 m/s,右侧为出口边界条件,前后面为对称面边界条件,上下面和翼型表面为无滑移壁面边界条件。在翼型表面增加边界层网格,边界层网格选择15层,为使y+<1.5,故增长速率设为1.1。网格基本尺寸设置为0.01 m,对三维直翼进行网格加密,其最小尺寸为2.5%的基本尺寸,目标尺寸为30%的基本尺寸。
2.3 涡流发生器(1) 涡流发生器结构参数及安装位置
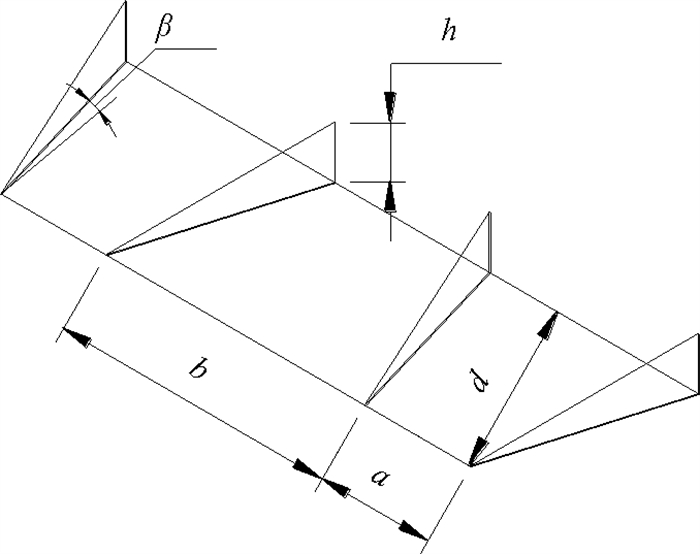
涡流发生器的5个主要参数如图 2所示,其涡流发生器厚度为0.2 mm。为了模拟每对涡流发生器之间的相互作用,设置了三对涡流发生器。
|
图 2 涡流发生器主要参数图 Fig. 2 Geometric parameters of VGs |
Mueller-Vahl等[14]的研究结果表明,涡流发生器安装在15%~20%弦长位置处达到的效果最好。在本文中,涡流发生器安装在20%弦长处。
(2) 涡流发生器的网格划分
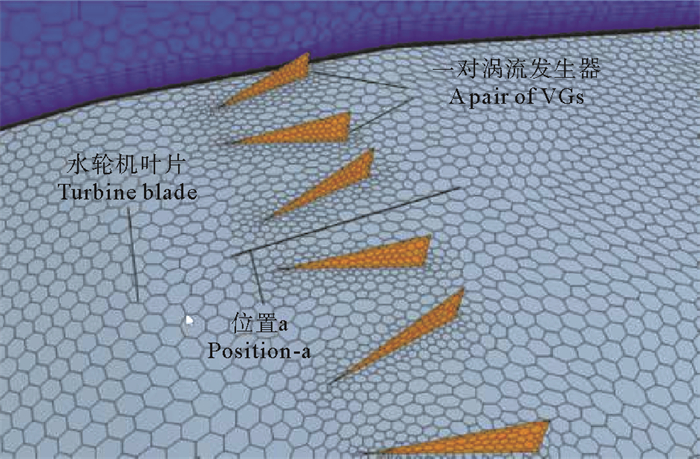
由于实际VGs只有0.2 mm的厚度,所以在划分网格时将VGs设置成一个厚度为0的面,0.2 mm的尺寸太小,生成网格的质量比较差,影响仿真结果。另外这样处理最大的好处有:避免了重新建立模型和生成网格,大大提高了效率;只需通过将VGs所在面转换成interface,就可以在同一套网格下对比有无VGs时翼型的升阻力特性,避免了因为网格不同而引起的数值误差[15]。涡流发生器处的网格结构如图 3所示。
|
图 3 涡流发生器网格结构 Fig. 3 Mesh in the local region around VGs |
采用耦合了转捩模型的SST k-ω湍流模型对基础翼型,即不带VGs的三维直翼进行数值仿真,选择与文献[16]中的案例相同的弦长和雷诺数等条件,得到的数值仿真结果与其实验结果进行比较,如表 1所示,由于仿真的条件设置较为理想化,比如水的密度设为恒定值,流动性质为不可压缩流动,所以计算得出的数值定会与实验数值有所偏差,但误差值在5%以内,可以认为仿真的结果是可信的。
|
|
表 1 数值验证与网格无关性验证 Table 1 Numerical verification and grid independence validation |
进行数值模拟时为了排除网格变化所带来的影响,选用攻角为23°,VGs1的仿真数据进行网格无关性验证。选取的网格策略及测试结果如表 1所示。由表中的结果可知,在网格总数116万左右时,数值模拟所得的升力系数和阻力系数变化小于2.5%,继续增加网格数量,数值模拟结果的精度提升不再明显,数值模拟的求解时长显著增加。综合以上选择Mesh2中的网格进行研究。
2.5 对照模型为了验证涡流发生器的输入参数对翼型性能的影响,本文共仿真了7组模型,分别改变涡流发生器的高度、长度和每对涡流发生器之间的间距来模拟其性能,7组涡流发生器模型的数据如表 2所示。
|
|
表 2 涡流发生器的参数 Table 2 The main parameters of VGs |
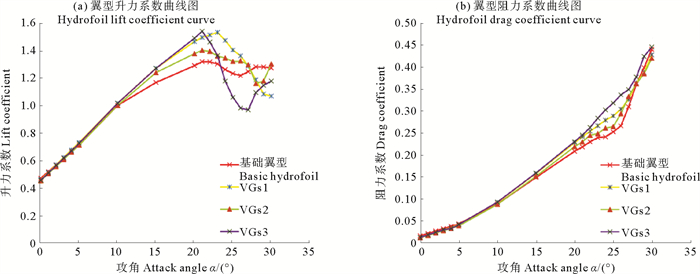
如图 4所示,涡流发生器对翼型性能的影响是通过比较有无VGs的情况得到的。在图 4(a)中,可以清楚地看到升力系数随着攻角线性增加,直到流动分离开始产生影响。对于VGs(VGs1和VGs2)的情况,升力系数曲线与失速前基础翼型的升力系数曲线基本一致,而采用VG会引起摩擦而产生轻微的阻力损失。随着攻角的增大,失速现象出现,VGs使翼型的失速攻角从21°提高到了23°。升力系数Cl的最大值出现在失速之前,使用VGs明显增加。随着攻角继续增大,达到失速攻角之后,此时涡流发生器对流动分离现象已不起作用,升力大幅度下降,阻力急剧增加,如图 4(b)所示。
|
图 4 涡流发生器高度对翼型性能的影响 Fig. 4 Effect of VGs height on hydrofoil performance |
图 4还显示了涡流发生器高度对翼型性能的影响。升力系数曲线的比较如图 4(a)所示,与VGs2和VGs3相比,在VGs1的情况下实现了更好的性能提升,在α=23°处产生Clmax值。VGs2具有更低的高度,VGs3具有更高的高度,其他参数值相同,这说明合理的涡流发生器高度才能对翼型性能提升达到最佳效果。在翼型阻力方面,随着涡流发生器高度的增加,阻力增加得也较为显著,图 4(b)也证实了这一点。
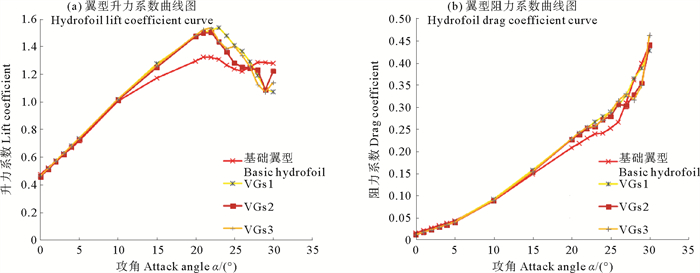
3.2 涡流发生器长度对翼型性能影响图 5给出了不同长度的涡流发生器对翼型的影响。VGs1、VGs4和VGs5是除了长度不同其他参数相同的三个模型。升力系数曲线如图 5(a)所示,从图中可以看出,VGs1在改善升力系数方面表现得最好。如图 5(b)所示,随着涡流发生器的长度增加,阻力也随之增大。
|
图 5 涡流发生器长度对翼型性能的影响 Fig. 5 Effect of VGs length on hydrofoil performance |
图 6给出了相邻一对涡流发生器之间的间距对翼型的影响。升力系数曲线图如图 6(a)所示,从图中可以看出,不同间距的涡流发生器对翼型升力都有一定的提升,但不同间距的涡流发生器对翼型的影响差距不大,其中,间距为25 mm的涡流发生器的提升效果稍好一些。如图 6(b)所示,阻力系数相差不大,可以看出每对涡流发生器之间的间距不同对其阻力的影响很小。

|
图 6 每对涡流发生器之间间距对翼型性能的影响 Fig. 6 Effect of the spacing between each pair of VGs on hydrofoil performance |
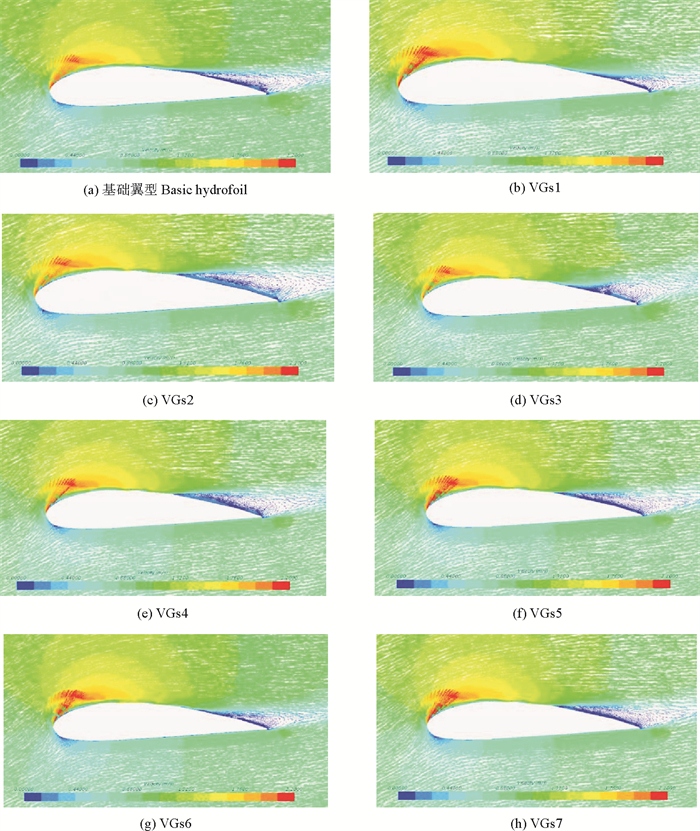
为进一步说明涡流发生器在翼型上的性能,分析涡流发生器周围的流场。图 7显示了叶片位置a(见图 3)处在攻角α=23°时有和没有涡流发生器的模型之间的流线图的比较。图 7(a)中,在攻角α=23°处,基础翼型发生了明显的流动分离现象,基础翼型的流线无法保持附着在吸力侧表面。在分离的区域内,很明显可以看到与自由流相反的反向流动。与基础翼型相比,VGs1在相同攻角下可以明显看出涡流发生器对流动分离现象具有抑制延迟作用,如图 7(b)所示。另外,从图 7(e)、(f)中可以看出长度较短的14 mm和长度较长的20 mm的涡流发生器对流动分离的控制并不显著。
|
图 7 在α=23°的情况下,基础翼型和7种VGs在位置a的速度流线图 Fig. 7 Velocity streamline diagram of basic hydrofoil and seven kinds of VGs at position-a at α=23° |
此外,与基础翼型相比,在有涡流发生器的情况下,流动分离现象都有一定程度的抑制,流体可以较好地附着到表面,如图 6(b)所示。其中,在有涡流发生器的情况下,不管是从升力系数曲线图还是速度流线图中都能看出,VGs1对翼型性能的提升和流动分离的抑制作用都达到了最佳情况。
当α=23°时,7种VGs情况下尾迹区X方向的涡量云图如图 8所示,取X =0.14 m,对应23%弦长处。随着X的增加,反向旋转的涡流会在下游区域逐渐扩展。水流经过一对涡流发生器会在VGs之间产生两个反向旋转的涡流,通过这种方式,所产生的涡流将边界层外部流体能量带入到边界层内,增加了边界层底部的流质的能量,使得翼型表面边界层内部的层流状态提前转捩为湍流边界层,因为湍流流质具有较好的抗分离能力,所以就可以有效的延迟边界层的分离,从而最终达到改善翼型性能的目的。7种VGs的作用效果比较表明,高度相对较大的VGs3和长度相对较长的VGs5会产生较强的涡旋,但是在提升翼型升力和控制流动分离方面,并不比VGs1好,这说明VGs的尺寸并不是越大越好,存在一个最佳改善翼型性能的VGs尺寸。

|
图 8 α=23°时,7种涡流发生器尾迹区X方向的涡量云图 Fig. 8 Vorticity cloud map in X direction of wake region of 7 kinds of VGs at α=23° |
本文建立了带和不带VGs的NACA 4418翼型潮流能水轮机叶片三维直翼模型,验证了VGs对直翼翼型的水动力性能影响。主要结论是:
(1) VGs可以有效地提高翼型的最大升力系数,并且可以使该翼型的失速攻角从21°延迟到23°。
(2) 更大尺寸的VGs会产生较强的涡旋,但是在提升翼型升力和控制流动分离方面,并不是最好的,这说明VGs的尺寸在改善翼型的水动力学性能方面并不是越大越好。
(3) 在本次研究中,VGs1不仅对翼型的升力提升,而且对流动分离的抑制都起到了最佳效果,这说明VGs不同的尺寸组合对翼型的水动力性能的改善起重要作用,这是之后研究的一个重要方向。
| [1] |
袁鹏, 陈超, 王树杰, 等. 潮流能水平轴水轮机翼型几何参数对其转捩特性的影响研究[J]. 太阳能学报, 2020, 41(6): 156-163. Yuan P, Chen C, Wang S J, et al. Study on the influence of the airfoil geometric parameters of tidal energy horizontal axis turbine on its transition characteristics[J]. Acta Energiae Solaris Sinica, 2020, 41(6): 156-163. (  0) 0) |
| [2] |
李应红, 梁华, 马清源, 等. 脉冲等离子体气动激励抑制翼型吸力面流动分离的实验[J]. 航空学报, 2008(6): 1429-1435. Li Y H, Liang H, Ma Q Y, et al. Experiments on aerodynamic excitation of pulse plasma to suppress flow separation of airfoil suction surface[J]. Acta Aeronautica et Astronautica Sinica, 2008(6): 1429-1435. DOI:10.3321/j.issn:1000-6893.2008.06.004 (  0) 0) |
| [3] |
吴映芳, 赵春妮, 张立新, 等. 涡流发生器在风力发电机组叶片上的应用[J]. 天津科技, 2018, 45(9): 80-83. Wu Y F, Zhao C N, Zhang L X, et al. Application of vortex generators on wind turbine blade[J]. Tianjin Science and Technology, 2018, 45(9): 80-83. DOI:10.3969/j.issn.1006-8945.2018.09.025 (  0) 0) |
| [4] |
叶叶沛. 涡流发生器原理和设计[J]. 西飞科技, 1996(2): 2-5. Ye Y P. Principle and design of vortex generators[J]. Xifei Technology, 1996(2): 2-5. (  0) 0) |
| [5] |
Taylor H D. The Elimination of Diffuser Separation by Vortex Generatiors[R]. Connecticut: United Aircraft Corporation Report, 1947.
(  0) 0) |
| [6] |
Gao L Y, Zhang H, Liu Y Q, et al. Effects of vortex generators on a blunt trailing-edge airfoil for wind turbines[J]. 2015, 76: 303-311.
(  0) 0) |
| [7] |
张进, 余春锦, 张彬乾. 微型涡流发生器对超临界翼型升阻特性影响实验研究[J]. 机械科学与技术, 2016, 35(9): 1461-1465. Zhang J, Yu C J, Zhang B Q. Numerical simulation research on the effect of transition on the aerodynamic performance of wind turbine vortex generators[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(9): 1461-1465. (  0) 0) |
| [8] |
王嘉诚. 基于CFD的三角翼式涡发生器设计与分析[D]. 南京: 南京航空航天大学, 2018. Wang J C. Design and Analysis of Delta-Wing Vortex Generators Based on CFD[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. (  0) 0) |
| [9] |
赵振宙, 李涛, 王同光, 等. 转捩对风力机涡流发生器气动性能影响的数值模拟研究[J]. 中国电机工程学报, 2016, 36(4): 1036-1041. Zhao Z Z, Li T, Wang T G, et al. Numerical simulation research on the effect of transition on the aerodynamic performance of wind turbine vortex generators[J]. Proceedings of the Chinese Society for Electrical Engineering, 2016, 36(4): 1036-1041. (  0) 0) |
| [10] |
Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables—Part Ⅰ: Model formulation[J]. Journal of Turbomachinery, 2006, 128(3): 57-67.
(  0) 0) |
| [11] |
Langtry R B, Menter F R, Likki S R, et al. A correlation-based transition model using local variables—Part Ⅱ: Test cases and industrial applications[J]. Journal of Turbomachinery, 2006, 128(3): 413-422. DOI:10.1115/1.2184352
(  0) 0) |
| [12] |
Tomac M, Pettersson K, Rizzi A. Calibration and Verification of a γ-Reθ Transition Prediction Method for Airfoil Computations[C]. Oriando, Florida: Aiaa Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2006: 281-290.
(  0) 0) |
| [13] |
黎作武, 陈江, 陈宝, 等. 风力机组叶片的先进翼型族设计[J]. 空气动力学学报, 2012, 30(1): 130-136. Li Z W, Chen J, Chen B, et al. Design of advanced airfoil families for wind turbines[J]. Acta Aerodynamica Sinica, 2012, 30(1): 130-136. (  0) 0) |
| [14] |
Mueller-Vahl H, Pechlivanoglou G, Nayeri CN, et al. Vortex Generators for Wind Turbine Blades: A Combined Wind Tunnel and Wind Turbine Parametric Study[C]. Copenhagen Denmark: Am Soc Mech Eng, 2012: 899-914.
(  0) 0) |
| [15] |
焦建东. 加装涡流发生器风力机叶片的气动性能研究[D]. 北京: 华北电力大学, 2014. Jiao J D. Research on Aerodynamic Performance of Wind Turbine Blades with Vortex Generators[D]. Beijing: North China Electric Power University, 2014. (  0) 0) |
| [16] |
袁新, 徐利军. 水平轴风力机翼型大攻角分离流动的数值模拟[J]. 太阳能学报, 1997, 18(1): 35-40. Yuan X, Xu L J. Numerical simulation of separated flow of horizontal axis wind turbine airfoil at large angle of attack[J]. Acta Energiae Solaris Sinica, 1997, 18(1): 35-40. (  0) 0) |
2. Qingdao Municipal Key Laboratory of Ocean Renewable Energy, Qingdao 266100, China
 2022, Vol. 52
2022, Vol. 52


