2. 军事科学院国防工程研究院,北京 100036
随着海洋科技的不断发展,人类探测领域已经从近海逐步跨入深海乃至超深海。深海领域对技术要求在不断提高,同时,需要更加先进的深海设备,因此深海设备从设计研发、生产到使用,都需要更大的发展及进步[1-2]。
本文所研究的水下中部悬置构筑物不具有动力系统,不具备自主航行的能力,通过锚链固定在海面以下,主要功能是为人类深海活动的提供补给,为深潜器提供燃料和装备,为深海勘察、采集、观测和资源开发等众多与深海环境资源有关的人类活动提供支持,提高深海作业的效率和安全性。因此,对水下中部悬置构筑物进行研究对促进深海资源探测的发展,具有重要的理论及实践意义。
韦起贤[3]采用双向流固耦合的数值模拟方式对球形、圆柱半球形、碟形平放和立放四种情况下构筑物的稳定性进行了研究。研究表明碟形是构筑物相对合理的结构外形,其在双向流固耦合设置中将构筑物离水面最远处设定为固定约束,只能够转动,没有X、Y和Z方向的位移。可以在一定程度上反应形状对稳定性的影响,但固定约束与实际情况的缆绳约束完全不相符。
本文将采用Aqwa模块,模拟缆绳对构筑物的约束,同时比较系泊方式和结构外形对水下中部悬置构筑物稳定条件的影响,为研究构筑物的合理外形提供参考。
1 环境参数及设计条件综合考虑可能的应用场景选定了200 m作为水深开展研究。通过查阅大量的国内外文献资料,当构筑物处于200 m水深时,波浪对其造成的影响可以忽略,故主要考虑洋流对构筑物可能造成的影响。研究显示中国近海200 m水深时最大流速不会超过2 m/s,因此本文从最不利荷载的角度出发,以2 m/s的流速为基础研究不同系泊方式和结构外形对构筑物稳定性的影响[3]。因200 m水深的铅直流单位一般是10-5 cm/s[4],速度较小,因此只考虑水平流速。
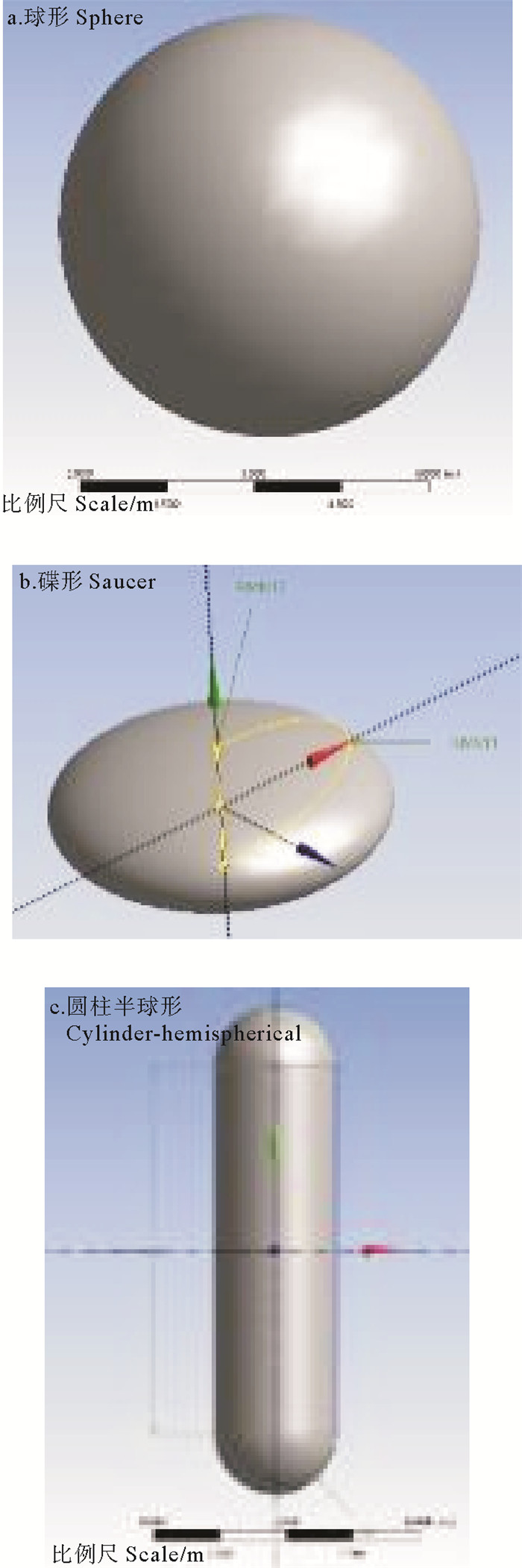
构筑物的形状初步选为碟形、圆球形、圆柱-半球形,如图 1所示。体积选择200和1 000 m3两个量级的尺寸如表 1所示。
|
图 1 海洋中部悬置构筑物形状 Fig. 1 Shape of suspended mid-ocean structures |
|
|
表 1 三类构筑物尺寸 Table 1 Three types of structures dimension |
Aqwa(Advanced quantiative wave analysis)模块作为大学、研究机构、海洋工程设计公司的重要浮体分析工具之一,其主要解决浮体在环境载荷作用下的运动响应、系泊定位、海上安装定位、船舶航行以及波浪载荷传递等方面的问题[5-8]。本文采用有限体积法离散,通过ANSYS Workbench平台中的Fluent模块计算构筑物在水流作用下的阻力,计算出的阻力作为水流力系数矩阵导入到该平台的Aqwa模块,再进行构筑物稳定性分析。
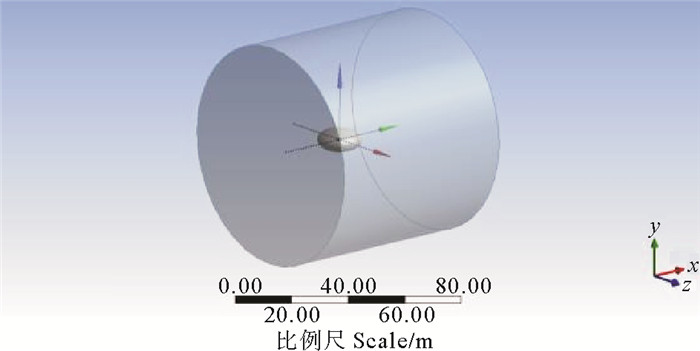
2.1 流场边界流域设置越大越好,可以忽略壁面对构筑物运动的影响,但流域设置过大,势必网格数量增多,从而影响计算效率,为保证模型周围流场得到充分发展,本文流场大小参考文献[9],建立圆柱形流域,模型的几何中心位于坐标原点。流域设置:前端长度为构筑物长度3倍;后端长度为构筑物长度4倍;直径为构筑物直径的10倍[9](见图 2)。
|
图 2 计算域模型 Fig. 2 Computation domain model |
采用Geometry模块进行流场域的建模,为保证全部区域都能划分成六面体网格,对流场进行切分,面与面之间两两对立[10]。
采用Mesh模块对已经切分好的流场进行网格划分,网格数量将很大程度影响计算效率和准确性,在靠近构筑物的附近网格应该尽可能的细一些,而距离构筑物很远的部分的网格可以设置大一些。参考孙梦瑶[11]的论文,第一层网格高度按照公式来确定:
| $ y^{+}=0.172(\Delta y / L) \operatorname{Re}^{0.9}。$ |
式中y+=40。
网格划分情况如图 3所示。

|
图 3 流场网格 Fig. 3 The flow field grid |
参考文献[3],本次研究选择了雷诺平均N-S方程,采用RNG k-ε湍流模型设置求解。采用稳态求解器,对压力速度耦合项选取SIMPLE算法进行解耦;采用有限体积法离散动量方程,其中对流项采用二阶迎风差分格式,扩散项采用中心差分格式;离散得到的代数方程采用Gauss-Seidel迭代求解[12]。
基于雷诺平均的N-S方程为:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial\left(\rho u_j\right)}{\partial x_j}=0,$ | (1) |
| $ \begin{gathered} \frac{\partial\left(\rho u_i\right)}{\partial t}+\frac{\partial\left(\rho u_i u_j\right)}{\partial x_j}= \\ \rho f_i-\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_i}\left[\left(\mu+\mu_i\right)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3} \frac{\partial u_{\mathrm{k}}}{\partial x_{\mathrm{k}}} \delta_{i j}\right)\right]。\end{gathered} $ | (2) |
RNG K-Epision湍流模型的k和ε方程如下:
| $ \rho \frac{\partial k}{\partial t}+\rho \frac{\partial}{\partial x_i}\left(k u_i\right)=\frac{\partial}{\partial x_i}\left(\alpha_k \mu_{\mathrm{eff}} \frac{\partial k}{\partial x_j}\right)+G_{\mathrm{k}}+G_{\mathrm{b}}-\rho \varepsilon-Y_{\mathrm{M}}, $ | (3) |
| $ \begin{gathered} \rho \frac{\partial \varepsilon}{\partial t}+\rho \frac{\partial}{\partial x_i}\left(\varepsilon u_i\right)= \\ \frac{\partial}{\partial x_j}\left(\alpha_{\varepsilon} \mu_{\mathrm{eff}} \frac{\partial \varepsilon}{\partial x_{\mathrm{j}}}\right)+G_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_{\mathrm{k}}+G_{3 \varepsilon} G_{\mathrm{b}}\right)-C_{2 \varepsilon} \rho \frac{\varepsilon^2}{k}-R。\end{gathered} $ | (4) |
式中:ρ、p分别代表了流体密度、流体压强;x、u、f分别代表坐标分量、速度分量、惯性力分量;μ是分子黏性系数;μi是湍流黏性系数;k和ε分别代表湍流动能和耗散率;Gb表示平均速度梯度引起的湍流而产生的动能;αk和αε分别为k和ε有效普朗特数的倒数;μeff为等效黏性系数,
整个计算域边界分为入口、出口、壁面和外部边界,所研究的构筑物模型黏性绕流视为不可压缩流动,各边界条件设置如下:
(1) 入口:采用速度入口边界(Velocity inlet),设定来流速度大小,其余参数采用Fluent默认设置。
(2) 出口:压力出口边界(Pressure-outlet)。
(3) 壁面表面:设定构筑物表面为不可滑移壁面条件,设为wall。
(4) 外边界:计算域外边界为无滑移壁面(Wall)。
(5) 对称边界:将模型对称面所在平面,即计算域的对称面,设定为对称边界(Symmetry)。在对称面上,既没有质量的交换,也没有热量等其他物理量的交换,Fluent设定垂直于对称面的速度分量为零。在计算中,该边界条件不需要给定任何参数。
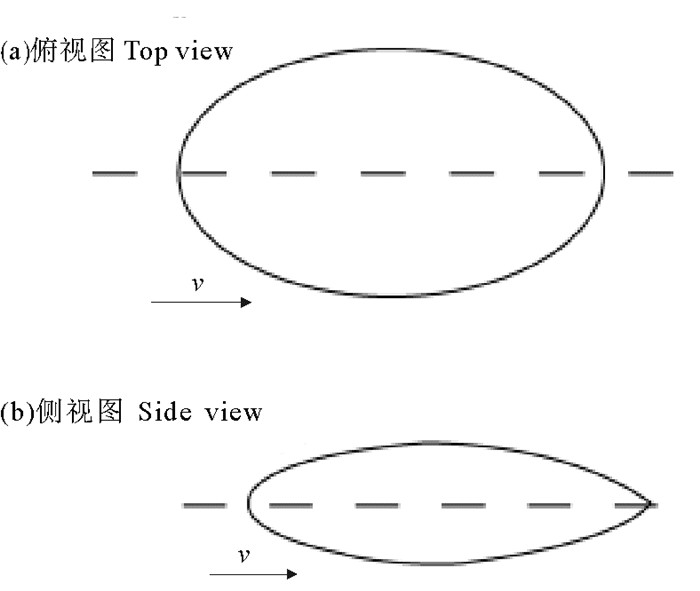
2.4 模型阻力计算方法验证早在2006年上海交通大学的张怀新等[13]就对新型蝶形潜水器进行了研究,证明了数值计算在潜水器阻力性能研究方面的应用价值。本文先对其模型进行计算和对比,验证计算方法的可行性与可靠性。其采用的模型示意图和尺寸分别如图 4和表 2所示。
|
图 4 潜水器布置图 Fig. 4 Outline of underwater vehicle |
|
|
表 2 潜水器主尺度要素 Table 2 Principle of underwater vehicle |
数值计算过程中,由于潜水器左右、上下对称,所以依然选取1/4模型进行计算,计算结果与原论文结果对比见表 3。
|
|
表 3 不同航速下潜水器的阻力 Table 3 Resistance of underwater vehicle at various speed |
从表 3可以看出,计算结果与实验结果非常的接近,误差都小于10%,说明该数值模拟方法的网格结构、数量以及所选取的计算参数是合理的。
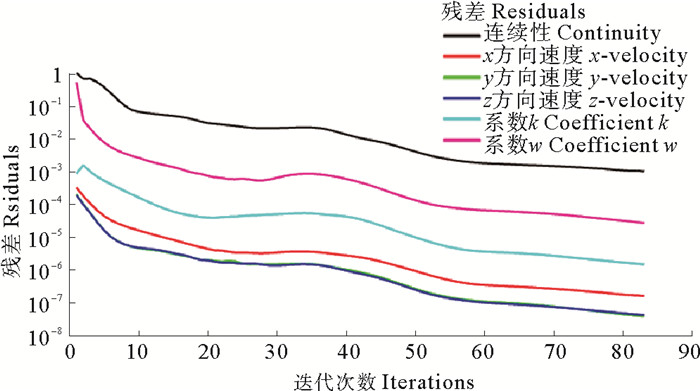
2.5 阻力计算结果通过Fluent软件计算3种不同形状的构筑物在2 m/s水流作用下受到的阻力,之前对模型进行了分块处理,生成了正交的六面体网格,网格的使用效果很好,计算80步就达到了收敛条件,残差图如图 5所示。
|
图 5 残差图 Fig. 5 Residual diagram |
|
|
表 4 200 m3构筑物仿真结果 Table 4 Simulation results of 200 m3structures |
|
|
表 5 1 000 m3仿构筑物仿真结果 Table 5 Simulation results of 1 000 m3 structures |
从上表可以看出, 比较三者的总阻力:200和1 000 m3的规律一致,碟形构筑物的阻力最小,球形构筑物次之,圆柱-半球形阻力最大,与球形和圆柱-半球形构筑物相比,碟形构筑物所受到的黏压阻力较小,黏压阻力又被称为旋涡阻力,它与构筑物尾部旋涡所消耗的能量有关,黏压阻力越小,所消耗的能量越少,构筑物尾部旋涡越少,所以上述结果表明碟形构筑物尾流中产生的旋涡较少,更适应在流场环境中的受力。
3 数值模拟结果分析在前面通过借助Fluent模块得到不同形状构筑物所受的阻力,可以得出,相比于圆球形和圆柱半球形,碟形构筑物受到的黏压阻力较小,尾流中的漩涡也会更少,在流场受力环境中会更加的稳定,因此将对碟形构筑物在不同系泊布置方案下运动响应做进一步研究,将前期Fluent模块计算出的阻力作为水流力系数矩阵导入到Aqwa模块再进行稳定性计算。
本文考虑的系泊布置形式可分为单索单点、三索单点和三索三点。
单索单点系泊即采用一根锚链进行连接,一端与构筑物连接,一端与海底相连[16],单索单点建模如图 6所示,200和1 000 m3碟形构筑物的锚链布置坐标和采用的锚链规格参数表 6所示。

|
图 6 单索单点系泊示意图 Fig. 6 Diagram of singer mooring |
|
|
表 6 单索单点锚链参数 Table 6 Anchor chain parameters of singer mooring |
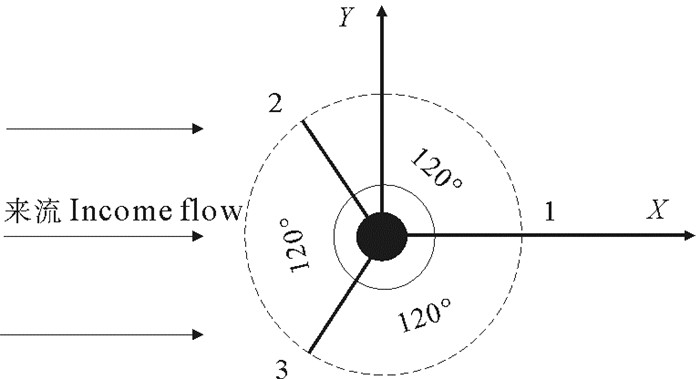
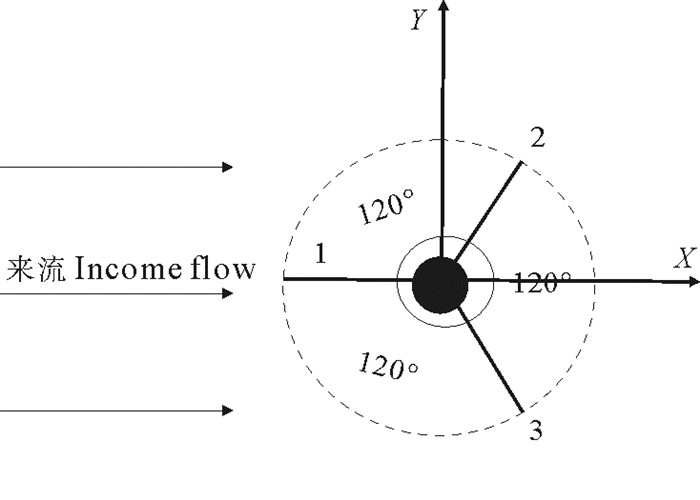
三索系泊即采用三根锚链连接,针对典型情况,设计了2种来流工况。每根锚链夹角为120°,海流从2根锚链中间流过[17],来流工况如图 7、8所示。
|
图 7 来流工况1 Fig. 7 Incomeflow condition 1 |
|
图 8 来流工况2 Fig. 8 Income flow condition 2 |
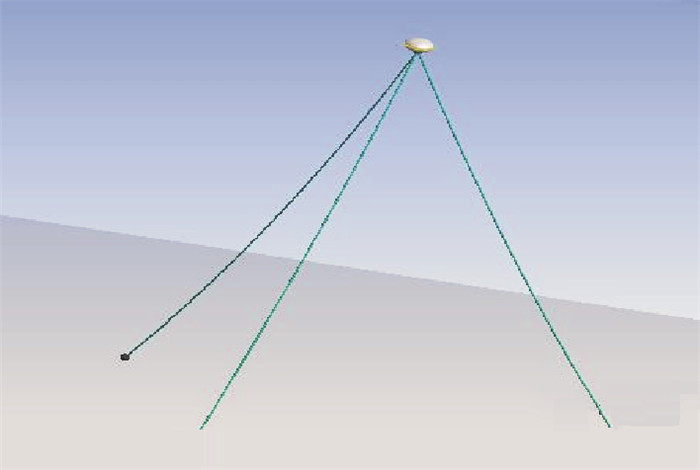
三索单点系泊即将三根锚链连在构筑物的同一点。三索单点系泊建模如图 9所示。表 7为200和1 000 m3构筑物锚链参数。
|
图 9 三索单点系泊示意图 Fig. 9 Diagram of singer-point mooring with three anchor chain |
|
|
表 7 三索单点锚链参数 Table 7 Anchor chain parameters of singer-point mooring with three anchor chain |
三索三点系泊即将3根锚链连接在构筑物上的3个位置。三索三点系泊建模如图 10所示。表 8为200和1 000 m3构筑物锚链参数。

|
图 10 三索三点系泊示意图 Fig. 10 Diagram of three-point mooring with three anchor chain |
|
|
表 8 三索三点锚链参数 Table 8 Anchor chain parameters of three-point mooring with three anchor chain |
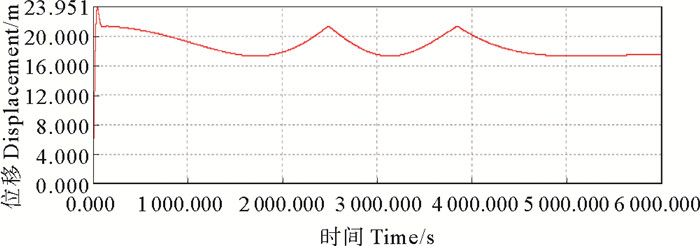
Aqwa模块忽略了水流作用对构筑物产生的涡激振动,因此无法准确模拟出构筑物在涡激振动下的振动响应。构筑物在单索单点系泊方式下的运动响应如图 11所示,可以看出构筑物的运动周期非常长,这与实际情况明显不符合,但Aqwa模块能够较为准确的模拟出构筑物在不同方向上的平均位移。本文的研究目的是比较不同系泊方式对构筑物在水中稳定性的影响,因此Aqwa模块能够满足研究要求。
|
图 11 X方向位移 Fig. 11 Displacement in X direction |
200 m3构筑物在不同系泊方式下的运动响应如表 9所示。由表可知,不同系泊方式下的构筑物都发生了不同程度上的运动。
|
|
表 9 200 m3构筑物运动响应 Table 9 200 m3structures motion responses |
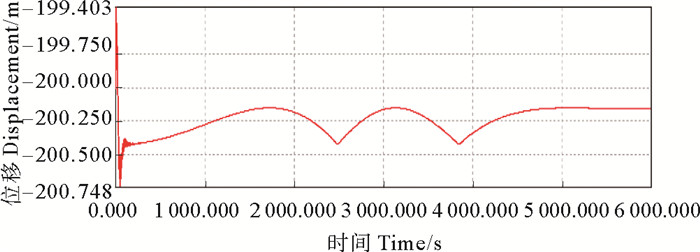
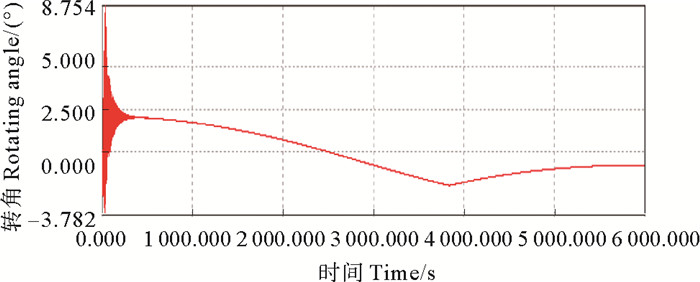
200 m3构筑物采用单索单点固定时不能够稳定下来,会在小幅度的范围内不停的波动,而采用3根锚链固定时,2种固定方式下的构筑物都能够稳定下来。构筑物采用单索单点固定时,沿水流方向上的位移最为剧烈,最大位移接近6 m。在3种系泊固定方式下,构筑物在Z方向上的位移都基本相同。采用三索三点系泊时,构筑物绕Y轴的转动角度最大,达到了-6.9°,因为靠近迎流面的2根锚链的张力比较大,背流面锚链的张力较小,在浮力的作用下,导致构筑物背流面那一侧高于迎流面那一侧,使转角增大。在三索单点系泊下,构筑物绕Y轴的转角最小,只有0.65°。在2种来流工况下,各个方向上的运动响应基本相同。
|
图 12 Z方向位移 Fig. 12 Displacement in Z direction |
|
图 13 绕Y轴转角 Fig. 13 Rotation angle around Y axis |
因此,从运动响应角度出发,当构筑物体积是200 m3时,采用三索单点系泊是最稳定的固定方式。
3.2 1 000 m3构筑物运动响应分析1 000 m3构筑物在不同系泊下的运动响应如表 10所示,在X方向上的位移和绕Y轴的转角都要比200 m3构筑物小,而在Z方向上的位移要偏大一些。
|
|
表 10 1 000 m3构筑物运动响应 Table 10 1 000 m3 structures motion responses |
1 000 m3构筑物采用单索单点系泊时也不能够稳定下来,会在小幅度的范围内不停的波动,而采用3根锚链固定时,2种固定方式下构筑物都能够稳定下来。构筑物采用单索单点固定时,沿水流方向上产生了较大的位移,最大位移接近2.8 m,其次是采用三索三点系泊方式,而采用三索单点系泊方式产生的位移最小。在3种系泊固定方式下,构筑物在Z方向上的位移也都基本相同。采用三索三点系泊时,构筑物绕Y轴的转动角度最大,达到了-2.7°,而其他2种系泊方式下的转角都在0.34°左右。在2种来流工况下,各个方向上的运动响应也基本相同。
综上可以得出结论,在体积为200和1 000 m3时,碟形构筑物采用三索单点固定方式的运动响应最小,采用单索单点固定方式会产生较大的运动响应,且可能会有较稳定的振动。在设定的2种来流工况下,构筑物的运动响应基本相同。
4 结论(1) 从水动力角度分析,相同体积下,碟形所受的流阻力最小,球形构筑物次之,圆柱-半球形阻力最大,所以碟形构筑物更适合在流场环境中受力。
(2) 碟形构筑物采用单根锚链固定时,在水流的作用下会产生较大的运动响应,且不稳定。而采用3根锚链进行固定时,碟形构筑物的位移都较小,且基本能够维持在稳定状态。
(3) 碟形构筑物采用三索单点系泊在各个方向上的位移会比采用三索三点系泊情况下的位移要更小。
| [1] |
Zhang T W, Tang J L, Qin S J, et al. Review of navigation and positioning of deep-sea manned submersibles[J]. Journal of Navigation, 2019, 72(4): 1021-1034. DOI:10.1017/S0373463319000080 (  0) 0) |
| [2] |
Pere R, Marc C, David R, et al. Intervention AUVs: The next challenge[J]. Annual Reviews in Control, 2015, 40: 227-241. DOI:10.1016/j.arcontrol.2015.09.015 (  0) 0) |
| [3] |
韦起贤. 悬置海洋中部构筑物外形优选与轻量化研究[D]. 青岛: 中国海洋大学, 2021. Wei Qixian. Shape Optimization and Lightweight of Suspended Structures in the Middle of the Ocean[D]. Qingdao: Ocean University of China, 2021. (  0) 0) |
| [4] |
魏泽勋. 中国近海环流及其季节变化的数值模拟[D]. 北京: 中国科学院研究生院, 2004. Wei Z X. Numerical Simulation of China's Offshore Circulation and Its Seasonal Variation[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2004. (  0) 0) |
| [5] |
张大朋, 白勇, 张彩悦, 等. 基于AQWA的自升式钻井平台水动力响应分析[J]. 石油工程建设, 2019(4): 33-39. Zhang Dapeng, Bai Yong, Zhang Caiyue. Hydrodynamic response analysis of jack-up offshore platform[J]. Petroleum Engineering Construction, 2019(4): 33-39. DOI:10.3969/j.issn.1001-2206.2019.04.008 (  0) 0) |
| [6] |
Cao Aixia, Sang Song, Sheng Jing, et al. Numerical simulation of twin-barge float-over installation on AQWA software[J]. Cluster Computing: The Journal of Networks, Software Tools and Applications, 2019, 22(4): 8735-8746. (  0) 0) |
| [7] |
纪仁玮, 张亮, 王树齐. 振荡浮子式双浮体波浪能装置的频域和时域分析[J]. 上海船舶运输科学研究所学报, 2019, 42(3): 19-27. Ji Renwei, Zhang Liang, Wang Shuqi. Frequency-domain and time-domain analysis of double-floating-body oscillating-buoy wave energy device[J]. Journal of Shanghai Ship and Shipping Research Institute, 2019, 42(3): 19-27. DOI:10.3969/j.issn.1674-5949.2019.03.004 (  0) 0) |
| [8] |
李宏伟, 管官. 基于AQWA的绳索位姿仿真计算研究[J]. 船舶标准化与质量, 2020, 288(3): 33-36. Li Hongwei, Guan Guan. Study on simulation of rope pose based on AQWA[J]. Shipbuilding Standardization and Quality, 2020, 288(3): 33-36. (  0) 0) |
| [9] |
刘天天. 自治水下航行器典型水动外形谱系研究[D]. 天津: 天津大学, 2017. Liu Tiantian. Study on Typical Hydrodynamic Shape Genealogy for Autonomous Underwater Vehicles[D]. Tianjin: Tianjin University, 2017. (  0) 0) |
| [10] |
郑冠超. 基于CFD近似模型的水下航行器节能优化研究[D]. 大连: 大连海事大学, 2017. Zheng Guanchao. Energy Efficient Optimization of Autonomous Underwater Vehicle Based on CFD Approximate Model[D]. Dalian: Dalian Maritime University, 2017. (  0) 0) |
| [11] |
孙梦瑶. 水下滑翔机粘性水动力数值模拟方法研究[D]. 天津: 天津大学, 2014. Sun Mengyao. Numerical Simulation of Viscous Hydrodynamics of Unmanned Underwater Glider[D]. Tianjin: Tianjin University, 2014. (  0) 0) |
| [12] |
赵鹏伟, 卢晓平, 孙玉明. 基于潜艇模型尾流湍流强度和耗散率的CFD模拟[J]. 中国舰船研究, 2014(3): 43-48. Zhao Pengwei, Lu Xiaoping, Sun Yunming. CFD simulation of the wake turbulence intensity and the dissipation rating of a submarine model[J]. Chinese Journal of Ship Research, 2014(3): 43-48. (  0) 0) |
| [13] |
张怀新, 潘雨村. 圆碟形潜水器阻力性能研究[J]. 上海交通大学学报, 2006, 40(6): 978-982. Zhang Huaixin, Pan Yucun. The resistance performance of a dish shaped underwater vehicle[J]. Journal of Shanghai Jiaotong University, 2006, 40(6): 978-982. DOI:10.3321/j.issn:1006-2467.2006.06.023 (  0) 0) |
| [14] |
王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. Wang F J. Computational Fluid Dynamics Analysis: Principles and Applications of CFD Software[M]. Beijing: Tsinghua University Press, 2004. (  0) 0) |
| [15] |
魏子凡, 俞强, 杨松林. 基于CFD不同AUV艇体的阻力性能分析[J]. 中国舰船研究, 2014(3): 28-37. Wei Zifan, Yu Qiang, Yang Songlin. Analysis of resistance for different types of AUVS based on CFD[J]. Chinese Journal of Ship Research, 2014(3): 28-37. (  0) 0) |
| [16] |
唐泽成. 点吸收式波浪能发电装置水动力性能研究与优化[D]. 杭州: 浙江大学, 2019. Tang Zecheng. Reasearch on the Hydrodynamic Characteristics and Optimization of the Point Absorber Wave Energy Converter[D]. Hangzhou: Zhejiang University, 2019. (  0) 0) |
| [17] |
Zhang Chi, Zhang Baoji. Analysis of the effect of supplying vessel on wave drift force of semi-submersible platform[J]. Open Journal of Modelling and Simulation, 2019, 7(3): 169-176. DOI:10.4236/ojmsi.2019.73009 (  0) 0) |
2. Institute of Defense Engineering, Academy of Military Sciences, Chinese People′s Liberation Army, Beijing 100036, China
 2023, Vol. 53
2023, Vol. 53

