2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237
海水是一种良导体,且处于不停的运动中。海水运动因切割地磁场会生成微弱的电流,进而在海水及其周围空间中激发感生电磁场。洋流又称海流,是指海水大规模、相对稳定的非周期性流动现象。它主要是受风力、压强梯度力、地球偏转力和湍流摩擦力的共同作用形成的,同时受海底地形、海岸线和岛屿等因素的影响[1]。海流根据驱动力主要可以分为风生海流和热盐环流两大类。在深水大洋中,前者只会影响到大洋的上层和中层,而热盐环流可以发生在大洋的整个区域[2]。
在探测海底地质结构的海洋电磁法研究中,海水运动电磁感应噪声是影响实测电磁数据质量的主要噪声和干扰。对这类电磁噪声进行压制或分离是海洋电磁(Marine electromagnetic, MT)数据处理解释中的一项重要工作[3-5]。
海流感应电磁场研究始于20世纪50年代。Longuet-Higgins等[6]较全面地阐述了海水运动感应电场理论,并分析了海流感应电场的特征。Sanford等[7]推导了海水深度变化和横向无界海洋中随时间变化的海流感应电场表达式。Larsen[8]提出了以电离层和海水为场源的海水运动感应电磁场控制方程,并讨论了均匀分层模型和非均匀导电薄层模型的海水运动感应电磁场特征。陈芸等[9]对国外关于海水运动感应电磁场研究的文献进行了综述及讨论。陈标等[10]结合毕奥萨法尔定律计算了地磁场垂直分量作用下的典型海流感应磁场。张自力[11]计算了海流感应电磁场。Bhatt[12]采用格林函数法计算了地磁场垂直分量作用下一维和二维匀速海水运动感应电磁场。
通常洋流的空间尺度大,宽度为10~1 000 km,深度为0.1~10 km,且在一定的区域内一致性较强,其路径、速率和方向在较长的时间内保持稳定,海流流动的速度在不同的海域各不相同,大的可达1 m/s,小的仅1 cm/s。由于在大多数情况下洋流水平速度比垂直速度大得多,因此实际中通常以研究水平洋流为主[13]。如果把海水看成是不可压缩的无旋液体,那么就可以把洋流简化为在流动方向上速度不变的均匀洋流[11]。林春生和任德奎[14]使用的海流模型是在与海水流动方向垂直的水平方向上洋流速度恒为常值,在垂直方向上海流层速度随着深度递减。为了更接近于实际海流,有学者讨论了在与海水流动方向垂直的水平方向上速度为正(余)弦变化的海流。陈标等[10]采用的海流模型为
在海洋中,磁场B由稳定的地磁场F和海流感应磁场b两部分组成,即B=F+b。考虑到短时间内有限小范围区域内地磁场F基本不变,且地磁场的幅值远大于海流感应磁场b的幅值,即
| $ \nabla \times {\bf{E}} = - \frac{{\partial {\bf{b}}}}{{{\partial _t}}}, $ | (1) |
| $ \nabla \times \mathit{\boldsymbol{b = }}{\mu _0}\mathit{\boldsymbol{J}}。$ | (2) |
式中感应电流密度
| $ \mathit{\boldsymbol{E = - }}\nabla \phi \mathit{\boldsymbol{ - }}\frac{{\partial \mathit{\boldsymbol{a}}}}{{{\partial _t}}}, $ | (3) |
式中ϕ为电磁场的标量势。
对于宽海流(海水的平均深度H远远小于海流的水平尺度L,即H≪L),当海流相速度不大于10m/s时,基于时变磁场的感应电场
| $ \nabla \phi = V \times \mathit{\boldsymbol{F - J/}}\sigma , $ | (4) |
对上述方程等式左右两边同时取散度,可得
| $ {\nabla ^2}\phi = \mathit{\boldsymbol{F}} · \nabla \times \mathit{\boldsymbol{V}}。$ | (5) |
在导出上式的过程中,本文利用了如下几个基本假设和定律:(1)地磁场是无旋的,即
建立笛卡尔直角坐标系,假定坐标原点位于海表面,z轴正向垂直向下,x轴指向正北,y轴指向正东(见图 1)。海水和海底介质的电导率分别为σ1和σ2,海水厚度为H,并假定海流流动方向与y轴平行,且海流仅限于海洋表层,其厚度和流速分别为H′和Vy=v0cos(αx),这里α=2π/L是海流速度变化的周期,L表示海流的半宽度。海洋的其余部分保持静止不动,海底沉积层的底部界面深度为Hs,其厚度为ΔHs=Hs-H。在通常情况下,海底沉积层的电导率为0.2~1S/m左右,而海底沉积层下覆地壳的电导率一般为0.000 1~0.03 S/m[15]。为了简化起见,本文将海底沉积层下覆地层近似看作为高阻绝缘地壳,其电导率为零。
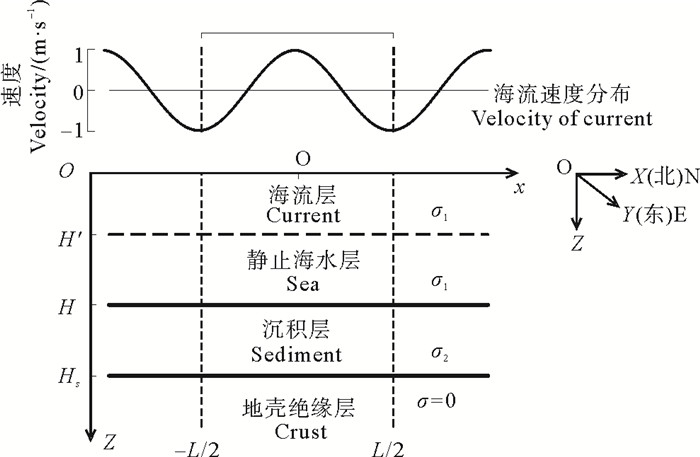
|
图 1 海流-地电模型 Fig. 1 Ocean current and geoelectrical conductivity model |
地磁场F为矢量场,可以分解成为垂直地磁场Fz和水平地磁场FH。应用叠加原理,海水及其周围空间中的感应电场可以看作为分别由垂直地磁场和水平地磁场而产生的感应电场之和。同理,感应电场的标量势也是由两部分组成的,即
| $ \phi {\rm{ = }}\phi {\rm{'}} + \phi {\rm{''}}。$ | (6) |
式中ϕ'和ϕ'分别为与垂直地磁场和水平地磁场有关的标量势。由式(6)可知,在海流层中,ϕ1′满足泊松方程:
| $ {\nabla ^2}{\phi _1}{\rm{' = - }}\alpha {v_0}{F_z}{\rm{sin}}\alpha x。$ | (7) |
在静止海水层和海底沉积层中,标量势ϕ′满足拉普拉斯方程:
| $ {\nabla ^2}{\phi _2}{\rm{'}} = 0, {\nabla ^2}{\phi _3}{\rm{'}} = 0。$ | (8) |
而在海流层、静止海水层和海底沉积层中,ϕ″均满足拉普拉斯方程:
| $ {\nabla ^2}{\phi _1}{\rm{''}} = 0, {\nabla ^2}{\phi _2}{\rm{'' = 0, }}{\nabla ^2}{\phi _3}{\rm{'' = 0}}。$ | (9) |
偏微分方程(7)和(8)的通解具有如下形式:
| $ \begin{array}{l} \phi _1^\prime = {a_1}{e^{ - \alpha z}}\sin \alpha x + {b_1}{e^{\alpha z}}\sin \alpha x + {v_0}{F_z}\sin \alpha x/\alpha , \\ \;\;\;\;\;\;\;\;\phi _2^\prime = {a_2}{e^{ - \alpha z}}\sin \alpha x + {b_2}{e^{\alpha z}}\sin \alpha x, \\ \;\;\;\;\;\;\;\;{\phi _3}^\prime = {a_3}{e^{ - \alpha z}}\sin \alpha x + {b_3}{e^{\alpha z}}\sin \alpha x。\end{array} $ | (10) |
式中:ai和bi(i=1, 2, 3)为待定系数,它们由标量势ϕ′所满足的边界条件而确定:在海表面上(z=0),电流密度的法向分量为零;在海流层和静止海水层分界面处(z=H′)以及海底界面上(z=H),标量势和电流密度的法向分量均连续;在沉积层底界面上(z=Hs),电流密度的法向分量为零。利用这些边界条件,可以求得所有6个待定系数的表达式:
| $ \begin{array}{l} {a_1} = - \frac{{{v_0}{F_z}{p_4}}}{{2\alpha {p_3}}}, {a_2} = \frac{{{v_0}{F_z}{e^{\alpha H}}{p_1}}}{{2\alpha {p_3}}}\sinh \left( {\alpha {H^\prime }} \right), \\ \;\;\;\;\;\;\;\;\;\;\;{a_3} = \frac{{{v_0}{F_z}{e^{\alpha {H_s}}}}}{{2\alpha {p_3}}}\sinh \left( {\alpha {H^\prime }} \right), \\ {b_1} = - \frac{{{v_0}{F_z}{p_4}}}{{2\alpha {p_3}}}, {b_2} = \frac{{{v_0}{F_z}{e^{ - \alpha H}}{p_2}}}{{2\alpha {p_3}}}\sinh \left( {\alpha {H^\prime }} \right), \\ \;\;\;\;\;\;\;\;\;\;\;{b_3} = \frac{{{v_0}{F_z}{e^{ - aHs}}}}{{2\alpha {p_3}}}\sinh \left( {\alpha {H^\prime }} \right)。\end{array} $ | (11) |
式中:
| $ \begin{array}{l} {p_1} = \cosh \left( {\alpha \Delta {H_s}} \right) + {\sigma _r}\sinh \left( {\alpha \Delta {H_s}} \right), \\ {p_2} = \cosh \left( {\alpha \Delta {H_s}} \right) - {\sigma _r}\sinh \left( {\alpha \Delta {H_s}} \right), \\ \;\;\;{p_3} = \cosh \left( {\alpha \Delta {H_s}} \right)\sinh (\alpha H) + \\ \;\;\;\;{\sigma _r}\sinh \left( {\alpha \Delta {H_s}} \right)\cosh (\alpha H), \\ {p_4} = \cosh \left( {\alpha \Delta {H_s}} \right)\sinh \left( {\alpha \left( {H - {H^\prime }} \right)} \right) + \\ {\sigma _r}\sinh \left( {\alpha \Delta {H_s}} \right)\cosh \left( {\alpha \left( {H - {H^\prime }} \right)} \right.。\end{array} $ |
这里σr=σ2/σ1为海底沉积层电导率与海水电导率之比,即海底沉积层的相对电导率,它是一个无量纲参数。
同理,可以求得各层中与水平地磁场有关的标量势(ϕ1″, ϕ2″, ϕ3″)的表达式。值得注意的是,在海表面和海流层与静止海水层分界面上,标量势ϕ′和ϕ″边界条件的表达式有所不同。在这两个分界面上,电流密度的法向分量是连续的。根据式(4),在海表面上,
在求得各层中的ϕ′和ϕ″后,由式(6)可得到海流层、静止海水层和海底沉积层中总标量势ϕ的表达式:
| $ \begin{array}{l} \;\;\;\;\;\;{\phi _1} = \frac{{{v_0}{F_z}}}{\alpha }\sin (\alpha x)\left[ {1 - \frac{{{\mathop{\rm scrcs}\nolimits} \left( {\alpha \left( {H - {H^\prime }} \right)} \right)}}{{{\mathop{\rm scrcs}\nolimits} (\alpha H)}}\cosh (\alpha z)} \right] \cdots - \\ \frac{{{v_0}{F_x}}}{\alpha }\cos (\alpha x)\left[ {\frac{{{\mathop{\rm ccrss}\nolimits} \left( {\alpha \left( {H - {H^\prime }} \right)} \right) - {\mathop{\rm ccrss}\nolimits} (\alpha H)}}{{{\mathop{\rm scrcs}\nolimits} (\alpha H)}}\cosh (\alpha z) + \sinh (\alpha z)} \right], \end{array} $ | (12) |
| $ \begin{array}{l} {\phi _2} = \frac{{{v_0}{F_z}}}{\alpha }\sin (\alpha x)\sinh \left( {\alpha {H^\prime }} \right)\left[ {\frac{{{\mathop{\rm ccrss}\nolimits} (\alpha (H - z))}}{{{\mathop{\rm scrcs}\nolimits} (\alpha H)}}} \right] \cdots + \frac{{{v_0}{F_x}}}{\alpha }\cos (\alpha x)\left[ {1 - \cosh \left( {\alpha {H^\prime }} \right)} \right]\frac{{{\mathop{\rm ccrss}\nolimits} (\alpha (H - z))}}{{{\mathop{\rm scrcs}\nolimits} (\alpha H)}}, \\ {\phi _3} = \frac{{{v_0}{F_z}}}{\alpha }\sin (\alpha x)\sinh \left( {\alpha {H^\prime }} \right)\frac{{\cosh \left( {\alpha \left( {{H_s} - z} \right)} \right)}}{{{\mathop{\rm scrcs}\nolimits} (\alpha H)}} \cdots + \frac{{{v_0}{F_x}}}{\alpha }\cos (\alpha x)\left[ {1 - \cosh \left( {\alpha {H^\prime }} \right)} \right]\frac{{\cosh \left( {\alpha \left( {{H_s} - z} \right)} \right)}}{{{\mathop{\rm scrcs}\nolimits} (\alpha H)}}。\end{array} $ |
式中:
| $ \begin{array}{l} {\mathop{\rm scrcs}\nolimits} (C) \equiv \sinh (C)\cosh \left( {\alpha \Delta {H_s}} \right) + \\ \;\;\;\;\;{\sigma _r}\cosh (C)\sinh \left( {\alpha \Delta {H_s}} \right), \\ {\mathop{\rm ccrss}\nolimits} (C) \equiv \cosh (C)\cosh \left( {\alpha \Delta {H_s}} \right) + \\ \;\;\;\;\;{\sigma _r}\sinh (C)\sinh \left( {\alpha \Delta {H_s}} \right)。\end{array} $ |
在求得总标量势后,对其求梯度
本文编写了模拟洋流感应电场的计算程序,用该程序可以计算正弦洋流感应电场以及电流密度。考虑由海水层、海底沉积层以及地壳绝缘层构成的地电模型,假设海水层和海底沉积层的电导率分别为σ1=3.4 S/m和σ2=0.34 S/m,海水深度为H=1 000m,其中海流层深度为H′=500m。假设海流流动方向与y轴平行,海流的半宽度为L=20km,其流速为Vy=v0cos(αx),取海底沉积层底界面埋深为Hs=2 000m,我们用本文方法和程序计算上述海流-地电模型洋流感应电场及电流,并分析其空间分布特征和影响因素。
2.1 洋流感应电流分布特征地磁场大小和方向可以用磁场矢量F来表示,单位nT。假设图 1中洋流-地电模型所在处的地理坐标为(50°N,110°E),利用国际地磁场模型WMM2019计算得到该处的地磁场,其垂直分量Fz和水平分量FH分别为56 164.4和20 193.2 nT(https://www.ngdc.noaa.gov/geomag/calculators/)。在下面讨论中,我们假定地磁场保持不变,为一常值,利用前面所述方法和程序可以计算得到洋流感应电场及电流密度。
模拟计算出基于垂直地磁场的洋流感应电流,分析其在垂直剖面XOZ内的分布特征(见图 2)。与y轴平行的洋流因切割地磁场而产生环形模式的感应电流,该电流在垂直剖面XOZ内流动,表层海流激发的电流在海流层内流动,但部分电流会流到静止海水层中,形成一个闭合回路(见图 2(a))。在通常情况下,海底沉积层的电导率为0.2~1S/m左右,具有较好的导电性,因而会发生电流“泄漏”,小部分电流会穿过海底界面进入海底沉积层中,然后再返回海水中,形成闭合电流回路(见图 2(b))。为了说明电流“泄漏”现象,图 2(a)中海底沉积层假设为理想绝缘层,泄露到海底介质中的电流大小与海底沉积层的电导率和厚度有关。更确切地说,它与海底介质的纵向电导即海底沉积层电导率和厚度的乘积有关。对此,我们将在后面做详细讨论。
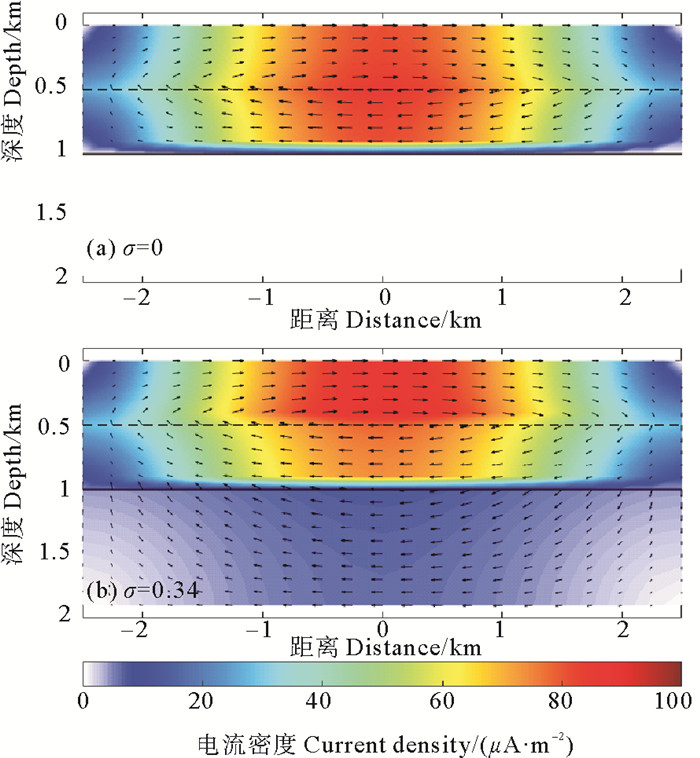
|
( (a)海底介质为绝缘层,(b)海底介质为导电沉积层。箭头表示洋流感应电流密度的方向,色标表示感应电流密度的大小。(a) Insulating seafloor; (b) Conductive seafloor sediments. Arrow and color code indicate the direction and magnitude of the current density respectively. ) 图 2 基于垂直地磁场的洋流感应电流在垂直剖面XOZ内的分布 Fig. 2 The distribution of the induced electric current in the vertical section generated by vertical geomagnetic field |
由图 2可见,基于垂直地磁场的洋流感应电流在垂直剖面(XOZ)上是关于x=0对称的,洋流感应电流密度的绝对值在x=0处最大,向两侧逐渐减小,这是由于正弦洋流速度Vy=v0cos(αx)为轴对称函数的缘故。洋流感应电流密度的方向和海流速度方向相关,当海流沿着y轴正向流动时,则大部分感应电流平行x轴流动。当海底介质为导电沉积层时,大部分电流集中在海流层和静止海水层中,但小部分电流流入海底沉积层中,即发生电流“泄露”。这部分电流的强度约为海流层感应电流的10%左右(见图 2(b))。泄露电流最终将穿过海底界面返回海水中,并与海水层中的电流汇合形成闭合回路。
考虑到有部分洋流感应电流与水平地磁场有关,模拟计算出基于水平地磁场的洋流感应电流。图 3为基于水平地磁场的洋流感应电流在垂直剖面XOZ内的分布。基于水平地磁场的洋流感应电流在垂直剖面(XOZ)内也是关于x=0对称的,但洋流感应电流密度的绝对值在x=0处最小,向两侧逐渐增大。绝大部分感应电流集中在海流层中,只有极少部分感应电流会流入静止海水层和导电沉积层中(见图 3(b)。当海底介质为绝缘地壳时,基于水平地磁场的洋流感应电流不会穿过海底界面,即不会发生电流“泄露”现象(见图 3(a))。根据式(6),模拟基于地磁总场的洋流感应电流在垂直剖面上的分布(见图 4),感应电流密度在XOZ上仍然是形成闭合回路,但是不再是关于x=0对称,尤其是在海流层区域。
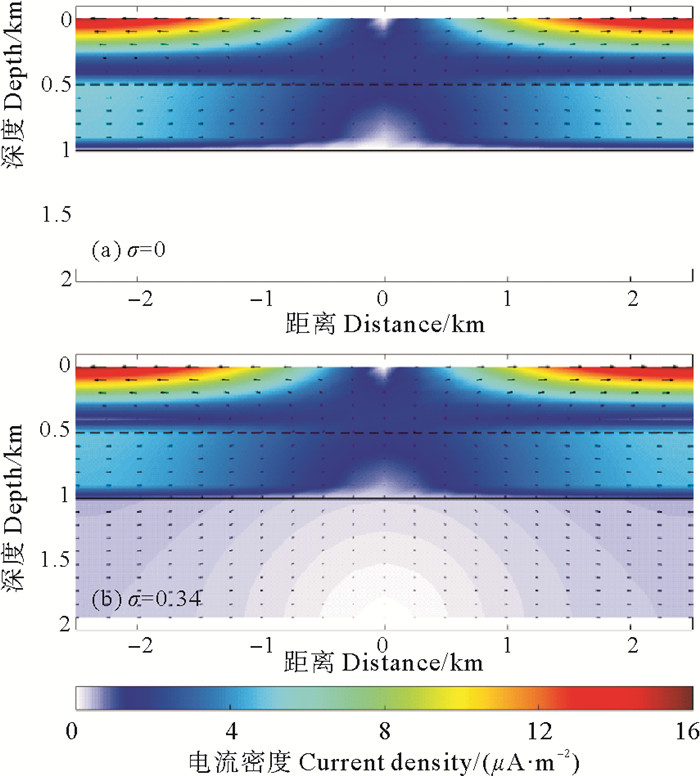
|
( (a)海底介质为绝缘层,(b)海底介质为导电沉积层。箭头表示洋流感应电流密度的方向,色标表示感应电流密度的大小。(a) Insulating seafloor; (b) Conductive seafloor sediments. Arrow and color code indicate the direction and magnitude of the current density respectively. ) 图 3 基于水平地磁场的洋流感应电流在垂直剖面XOZ内的分布 Fig. 3 The distribution of the induced electric current in the vertical section generated by horizontal geomagnetic field |
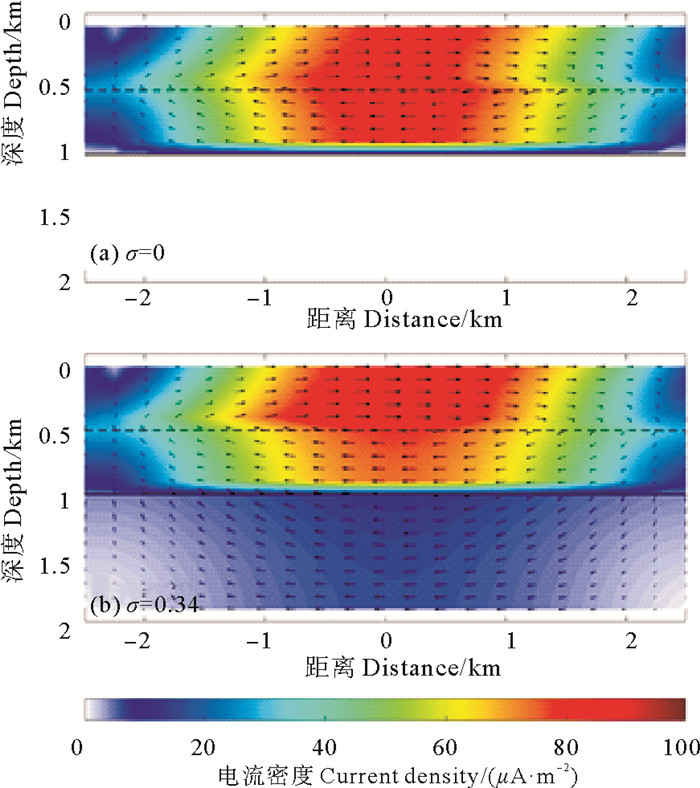
|
( (a)海底介质为绝缘层,(b)海底介质为导电沉积层。箭头表示洋流感应电流密度的方向,色标表示感应电流密度的大小。(a) Insulating seafloor; (b) Conductive seafloor sediments. Arrow and color code indicate the direction and magnitude of the current density respectively. ) 图 4 基于总地磁场的洋流感应电流在垂直剖面XOZ内的分布 Fig. 4 The distribution of the induced electric current in the vertical section generated by geomagnetic field |
由洋流感应标量势表达式(12)可知,影响洋流感应标量势以及由其导出的感应电场的主要参数为海流层厚度(H′)、海水厚度(H)、海底沉积层埋深(Hs)、海流水平尺度(L)和海水及海底介质的电导率(σ1和σ2)。将以上6个参数无量纲化,可以得到4个无量纲参数:纵横比H/L,海流层相对厚度H′/H,海底沉积层相对厚度(Hs-H)/H=ΔHs/H和海底介质相对电导率σr=σ2/σ1。下面我们分析以上4个无量纲参数对洋流感应电场的影响。
在本文前面推导宽海流感应电场表达式时,我们假定海水厚度远远小于海流水平尺度(即H≤L),且海流流动缓慢(假定海流流速不大于10 m/s),只有在这些条件下,洋流感应电场可以近似为标量势的负梯度,即
为了确定合适的纵横比,使得H/L满足
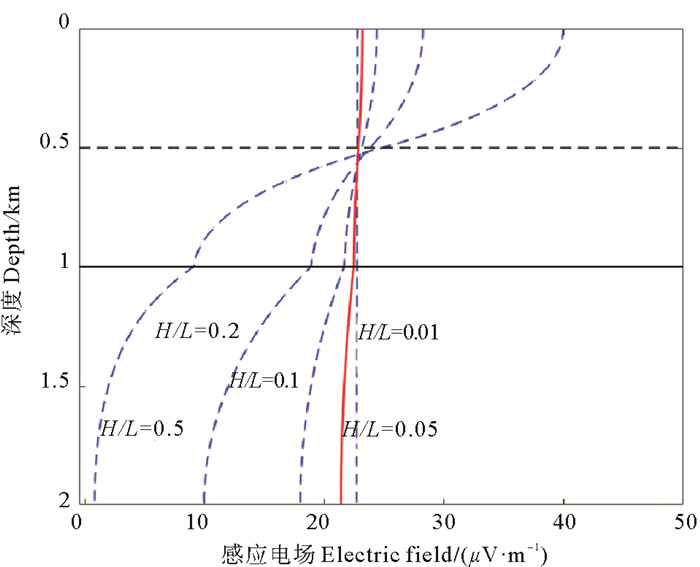
|
图 5 不同纵横比时洋流感应电场随深度的变化曲线 Fig. 5 Variation of the induced electric field with ocean depth under different aspect ratio |
海流层相对厚度H′/H反映流动海水在整个海水中所占的比例,可以理解为激发场源的相对范围。在厚度为1 000 m的海水中,假定海流层的厚度分别为0、250、500、750和1 000 m,采用本文所述方法和程序计算海底面处平行x轴剖面上洋流感应电场(见图 6)。图 6绘出了海流速度曲线,当海流层厚度为零时,不会产生感应电场,其值为零;海底界面处洋流感应电场的绝对值随着海流层厚度的增大而增大,当整个海水都成为海流层时,洋流感应电场最强;在海底面处平行x轴剖面上,洋流感应电场曲线呈余弦变化特征,即与海流速度变化形态一致。
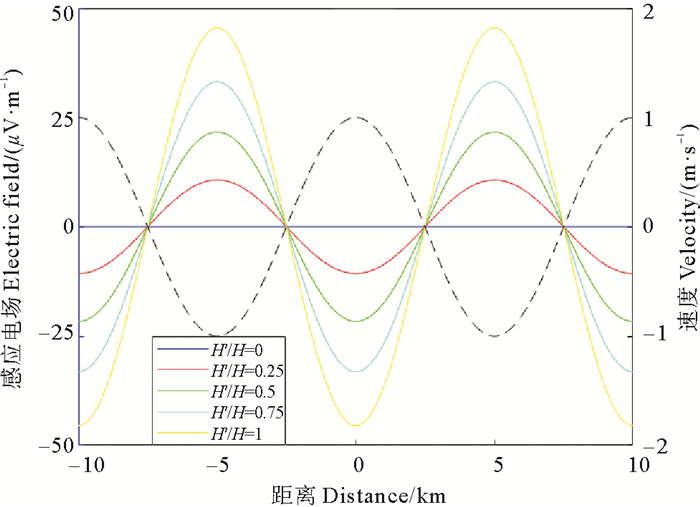
|
( 实线为海底界面处感应电场变化曲线,黑色虚线为海流速度变化曲线。Solid lines indicates the induced electric field. Black dashed indicates ocean current velocity. ) 图 6 海流层相对厚度H′/H对海底界面处感应电场的影响 Fig. 6 Variation of the induced electric field (solid lines) along the seafloor profile for different relative thicknesses of ocean currents |
为了分析海底沉积层对洋流感应电流导通能力的影响,引入沉积层电导系数λ,定义其为海底沉积层纵向电导与海水层纵向电导的比值,即
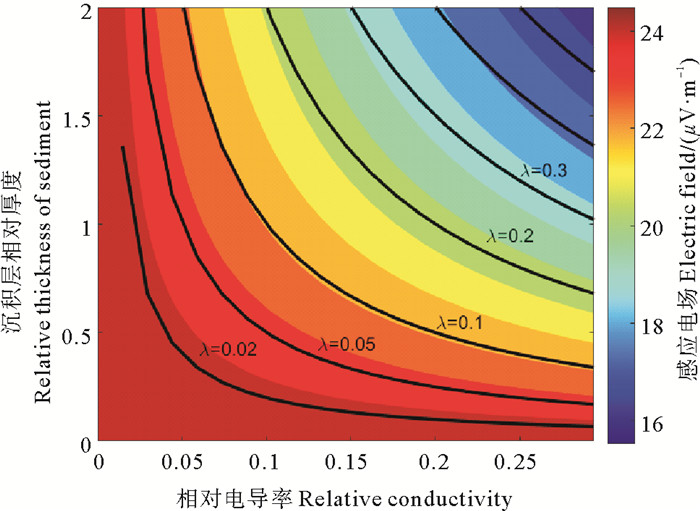
|
( 黑色曲线为沉积层电导系数λ的等值线。Black lines are contours of sediment conductance factor λ. ) 图 7 海底界面处洋流感应电场的绝对值与沉积层相对厚度和相对电导率的关系 Fig. 7 Variation of the induced electric field in the seafloor with the relative thickness and the relative conductivity of the sediment layer |
本文推导了水平地层正弦洋流激发的感应电场表达式,编写了计算程序,计算了一维地电模型正弦洋流感应电场,并分析了纵横比、海流层相对厚度、海底沉积层相对厚度和海底沉积层相对电导率等4个无量纲参数对洋流感应电场的影响。模拟结果表明,对于宽海流,基于垂直地磁场的洋流感应水平电场在垂直剖面上是均匀分布的;洋流感应电流为环形模式,仅在垂直剖面内流动,在海水和沉积层中形成闭合回路;洋流感应电流在沉积层中的流通能力取决于沉积层的纵向电导,随着沉积层纵向电导的不断增大,海底界面处感应电场幅值逐渐减小;海底界面处洋流感应电场的幅值随着海流层厚度的增大而增大。该结果对了解海流感应电磁场产生机理、分布规律、幅值大小以及其特性具有重要意义,并可以为海洋电磁探测中压制洋流感应电磁噪声方法研究奠定基础。
| [1] |
李庚伟. 海洋感应电磁场理论研究[D]. 北京: 中国地质大学(北京), 2012. Li Geng-wei. The Theory Research on Ocean Induction Electromagnetic Field[D]. Beijing: China University of Geosciences (Beijing), 2012. (  0) 0) |
| [2] |
单忠伟. 海流测量技术综述[J]. 声学与电子工程, 2011(1): 1-5. Dan Zhong-wei. A review of current measurement techniques[J]. Acoustics and Electronics Engineering, 2011(1): 1-5. (  0) 0) |
| [3] |
Chave A D, Filloux J H. Electromagnetic induction fields in the deep ocean off California: Oceanic and ionospheric sources[J]. Geophysical Journal of the Royal Astronomical Society, 1984, 77(1): 143-171. DOI:10.1111/j.1365-246X.1984.tb01929.x (  0) 0) |
| [4] |
魏文博, 邓明, 温珍河, 等. 南黄海海底大地电磁测深试验研究[J]. 地球物理学报, 2009, 52(3): 740-749. Wei Wen-bo, Deng Ming, Wen Zhen-he, et al. Experimental study of marine magnetotellurics in southern Huanghai[J]. Chinese J Geophysics, 2009, 52(3): 740-749. (  0) 0) |
| [5] |
于彩霞, 魏文博, 景建恩, 等. 希尔伯特-黄变换在海底大地电磁测深数据处理中的应用[J]. 地球物理学进展, 2010, 25(3): 1046-1056. Yu Cai-xia, Wei Wen-bo, Jing Jian-en, et al. Application of Hilbert-Huang transformation to marine magnetotelluric sounding data processing[J]. Progress in Geophysics, 2010, 25(3): 1046-1056. DOI:10.3969/j.issn.1004-2903.2010.03.045 (  0) 0) |
| [6] |
Longuet-Higgins M S, Stern M E, Stommel H M. The electrical field induced by ocean currents and waves, with applications to the method of towed electrodes[J]. Deep Sea Research, 1956, 3(2): 156-160. DOI:10.1016/0146-6313(56)90099-5 (  0) 0) |
| [7] |
Sanford, Thomas B. Motionally induced electric and magnetic fields in the sea[J]. Journal of Geophysical Research, 1971, 76(15): 3476-3492. DOI:10.1029/JC076i015p03476 (  0) 0) |
| [8] |
Larsen J C. An introduction to electromagnetic induction in the ocean[J]. Physics of the Earth & Planetary Interiors, 1973, 7(3): 389-398. (  0) 0) |
| [9] |
陈芸, 吴晋声. 海洋电磁学及其应用[J]. 海洋科学, 1992(2): 19-21. Chen Yun, Wu Jin-sheng. Marine electromagnetism and applications[J]. Marine Sciences, 1992(2): 19-21. (  0) 0) |
| [10] |
陈标, 祝传刚, 张铁军, 等. 典型海流磁场的数值模拟[J]. 青岛大学学报(自然科学版), 2001, 14(2): 1-3. Chen Biao, Zhu Chuan-gang, Zhang Tie-jun, et al. Numerical simulation of typical ocean current magnetic field[J]. Journal of Qingdao University, 2001, 14(2): 1-3. DOI:10.3969/j.issn.1006-1037.2001.02.001 (  0) 0) |
| [11] |
张自力. 海洋电磁场的理论及应用研究[D]. 北京: 中国地质大学(北京), 2009. Zhang Zi-li. Theory Research and Application of Ocean Electromagnetic Field[D]. Beijing: China University of Geosciences, 2009. (  0) 0) |
| [12] |
Bhatt K M. Motion Induced Noise in Marine Electromagnetic Data[D]. Germany: Technischen Universitat Carolo-Wilhelmina, 2011.
(  0) 0) |
| [13] |
张启升, 邓明, 刘宁, 等. 投弃式海流电场剖面仪研制[J]. 地球物理学报, 2013, 56(11): 3699-3707. Zhang Qi-shen, Deng Ming, Liu Ning, et al. Development of the expendable current profiler[J]. Journal of Geophysical Research, 2013, 56(11): 3699-3707. DOI:10.6038/cjg20131111 (  0) 0) |
| [14] |
林春生, 任德奎. 海流感应电磁场的分析与计算[J]. 海军工程大学学报, 2003(4): 21-24+43. Lin Chun-sheng, Ren De-kui. Calculation of electromagnetic field induced by ocean current[J]. Journal of Naval University of Engineering, 2003(4): 21-24+43. (  0) 0) |
| [15] |
Zoltan B Szuts. The Interpretation of Motionally Induced Electric Fields in Oceans of Complex Geometry[D]. Washington, USA: University of Washington, 2008.
(  0) 0) |
| [16] |
Szuts Z B. Relationship between ocean velocity and motionally induced electrical signals: 1. In the presence of horizontal velocity gradients[[J]. Journal of Geophysical Research: Oceans, 2010, 15(6): 267-271. (  0) 0) |
| [17] |
Hall M. Direct estimates and mechanisms of ocean heat transport[J]. Deep Sea Research Part A Oceanographic Research Papers, 1982, 29(3): 339-359. DOI:10.1016/0198-0149(82)90099-1 (  0) 0) |
| [18] |
朱心宇, 李予国. 有限水深海流感应电磁场数值模拟[J]. 中国海洋大学学报(自然科学版), 2020, 50(8): 109-114. Zhu Xin-Yu, LI Yu-Guo. Numerical simulation of electromagnetic field induced by ocean current in finite water depth[J]. Periodical of Ocean University of China, 2020, 50(8): 109-114. (  0) 0) |
| [19] |
索切尔尼科夫B B. 海洋中天然电磁场的理论基础[M]. 陈芸译. 北京: 海洋出版社, 1987. Sochernikov B B. Theoretical Basis of Natural Electromagnetic Fields in the Ocean[M]. Chen Yun Translation. Beijing: China Ocean Press, 1987. (  0) 0) |
2. Laboratory for Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China
 2022, Vol. 52
2022, Vol. 52


