2. 江苏科技大学船舶与海洋工程学院,江苏 镇江 212003
随着油气开发不断向深水海域扩展,钢悬链线立管以其安装简便、成本低、适应性强等优点得到广泛应用[1-2]。但是随着水深的增加,钢悬链线立管顶部张力需求增加,顶部浮体剧烈运动或恶劣环境荷载作用下,立管触地点易产生疲劳损伤。在钢悬链线立管部分长度上安装浮力模块,可以形成缓波形立管的系统布置形式。浮力和重力共同作用在细长的缓波形立管上,可以减小立管顶部张力,解耦立管触地点与顶部浮体运动的关系,从而提高立管的疲劳寿命[3-4]。
国内外学者对缓波形立管的研究相对较少,Li等[5]用三段悬链线模拟缓波形立管,求解立管的静力位形,但该理论无法考虑海流作用力,不能研究缓波形立管在海流作用下的结构响应;Wang等[6]建立缓波形立管的非线性大变形梁模型,研究立管在海流和内流作用下的形态和力学性能;孙丽萍等[7]运用Orcaflex软件建立缓波形立管分析模型,并对立管的布置参数进行敏感性分析;李艳等[8]利用三维集中质量法分析缓波形立管在平台静态与动态偏移下的有效张力,并与传统的悬链线立管进行比较;宋磊建等[9]利用Orcaflex软件对缓波形脐带缆进行参数敏感性分析,研究浮子段长度、浮力因子、浮子段起始位置及顶部悬挂角对脐带缆结构响应的影响。Orcaflex软件[10]采用集中质量模型模拟立管并进行时域分析,本文采用的柔性杆模型可以直接在全局坐标系下更有效地解决缓波形立管的大变形问题。该模型最初由Garrett[11]提出,并不断完善;但国内外学者运用柔性杆理论对立管进行静动力分析时都忽略了内流的影响。
本文采用细长柔性杆模型,建立考虑内流作用的缓波形立管运动方程,运用有限元法进行离散,基于Matlab平台编制相应计算程序,对海流、内流和浮体漂移与运动等荷载作用下的缓波形立管进行非线性静动力分析。
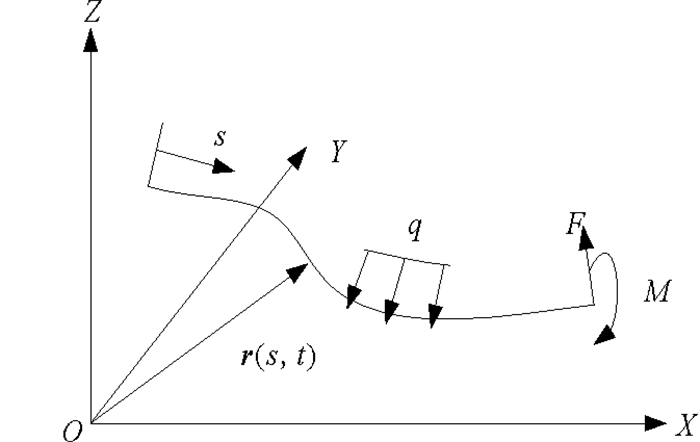
1 计算模型 1.1 柔性杆模型细长柔性杆模型如图 1所示,杆的位形由杆轴线位置表示,即空间曲线r(s, t),可以较好地解决立管的大变形问题。
|
图 1 柔性杆模型示意图 Fig. 1 Diagram of slender rods |
忽略转动惯量和剪切变形的影响,考虑内流作用的缓波形立管微元体平衡方程可由动量守恒和动量矩守恒获得:
| $ \mathit{\boldsymbol{F'}} + \mathit{\boldsymbol{q}} = \left( {\rho + {m_f}} \right)\mathit{\boldsymbol{\ddot r}}。$ | (1) |
| $ \mathit{\boldsymbol{M'}} + \mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{F}} + \mathit{\boldsymbol{m}} = 0。$ | (2) |
式中:F为轴线上的合力;q为立管单位长度施加的外力;ρ和mf分别为立管和内流单位长度的质量;M为轴线上的合力矩;m为单位长度的外力矩。细长结构物通常可以忽略扭矩和分布外力矩,则M=r'×EIr″, m=0。EI为抗弯刚度。
如果考虑柔性杆的伸长且伸长量为小量,则变形条件:
| $ \frac{1}{2}\left( {\mathit{\boldsymbol{r'}} \cdot \mathit{\boldsymbol{r'}} - 1} \right) \approx \frac{\lambda }{{EA}}。$ | (3) |
式中,λ=F·r'+(EIr″)'·r',EA为抗拉刚度。
杆的运动方程为:
| $ - {\left( {EI\mathit{\boldsymbol{r''}}} \right)^{\prime \prime }} + {\left( {\lambda \mathit{\boldsymbol{r'}}} \right)^\prime } + \mathit{\boldsymbol{q}} = \left( {\rho + {m_f}} \right)\mathit{\boldsymbol{\ddot r}}。$ | (4) |
缓波形立管底部与海床接触,本文采用弹性地基的文克勒模型[12]来模拟海床作用。
1.2 荷载分析缓波形立管处于复杂的海洋环境中,受到自身重力和周围流体的作用。
| $ \mathit{\boldsymbol{q}} = \mathit{\boldsymbol{w}} + {\mathit{\boldsymbol{F}}^s} + {\mathit{\boldsymbol{F}}^d}。$ | (5) |
式中:w、Fs、Fd分别为立管单位长度受到的重力、水静力和水动力。
| $ {\mathit{\boldsymbol{F}}^s} = \mathit{\boldsymbol{B}} + {\left( {\mathit{P}\mathit{\boldsymbol{r'}}} \right)^\prime }。$ | (6) |
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}^d} = {\rho _w}\frac{{{\rm{ \mathsf{ π} }}{D^2}}}{4}\mathit{\boldsymbol{\dot V}} + {C_a}{\rho _w}\frac{{{\rm{ \mathsf{ π} }}{D^2}}}{4}\left( {{{\mathit{\boldsymbol{\dot V}}}^n} - {{\mathit{\boldsymbol{\ddot r}}}^n}} \right) + \\ \frac{1}{2}{C_D}{\rho _w}D\left| {{\mathit{\boldsymbol{V}}^n} - {{\mathit{\boldsymbol{\dot r}}}^n}} \right|\left( {{\mathit{\boldsymbol{V}}^n} - {{\mathit{\boldsymbol{\dot r}}}^n}} \right)。\end{array} $ | (7) |
式中:B为立管单位长度受到的浮力;P为管内外压强差;ρw为海水密度;D为立管外径;Ca为附加质量系数;CD为拖曳力系数;V为水流速度。
本文采用细长体活塞流模型来模拟内流作用,即假设立管内部流体为一具有无限柔性的细长状柱体,其断面上每一点都具有相同的流速v,这样内流对立管微元体的作用力可以表示为[13]:
| $ \mathit{\boldsymbol{f}}\left( {s,t} \right) = - {m_f}\left( {\frac{{{\partial ^2}\mathit{\boldsymbol{r}}}}{{\partial {t^2}}} + 2v\frac{{{\partial ^2}\mathit{\boldsymbol{r}}}}{{\partial s\partial t}} + {v^2}\frac{{{\partial ^2}\mathit{\boldsymbol{r}}}}{{\partial {s^2}}}} \right)。$ | (8) |
代入荷载作用力,将运动方程和变形条件写成张量形式:
| $ \begin{array}{l} - \left( {\rho + {m_f}} \right){{\mathit{\boldsymbol{\ddot r}}}_i} - {C_A}\mathit{\boldsymbol{\ddot r}}_i^n - 2{m_f}v{{\mathit{\boldsymbol{\dot r'}}}_i} - {\left( {EI{{\mathit{\boldsymbol{r''}}}_i}} \right)^{\prime \prime }} + \\ {\left( {\bar \lambda {{\mathit{\boldsymbol{r'}}}_i}} \right)^\prime } + {{\mathit{\boldsymbol{\bar w}}}_i} + \mathit{\boldsymbol{\bar F}}_i^d = 0。\end{array} $ | (9) |
| $ \frac{1}{2}\left( {{{\mathit{\boldsymbol{r'}}}_n}{{\mathit{\boldsymbol{r'}}}_n} - 1} \right) - \frac{{\bar \lambda - P + {m_f}{v^2}}}{{EA}} = 0。$ | (10) |
利用有限元法将立管沿全长离散成N个单元,引入Hermite插值函数Al(s)和Pm(s),用单元两端节点处的变量Uil、λm来表示单元内部变量:
| $ {\mathit{\boldsymbol{r}}_i}\left( {s,t} \right) = {A_l}\left( s \right){U_{il}}\left( t \right)。$ | (11) |
| $ \bar \lambda \left( {s,t} \right) = {P_m}\left( s \right){{\bar \lambda }_m}\left( t \right)。$ | (12) |
式中:Al(s)、Pm(s)分别为二次、三次Hermite形函数;Uil(t)为单元两端节点处的位置向量和切线向量;λm(t)为单元两端节点和中点处的有效张力向量。
最终得到缓波形立管运动方程的矩阵形式:
| $ \begin{array}{l} \left( {{\mathit{\boldsymbol{M}}_{ijlk}} + \mathit{\boldsymbol{M}}_{ijlk}^a} \right){{\ddot U}_{jk}} + C_{ijlk}^f{{\dot U}_{jk}} + \left( {\mathit{\boldsymbol{K}}_{ijlk}^1 + } \right.\\ \left. {{{\bar \lambda }_n}\mathit{\boldsymbol{K}}_{nijlk}^2 - \mathit{\boldsymbol{K}}_{nijlk}^3} \right){U_{jk}} - {\mathit{\boldsymbol{F}}_{il}} = 0。\end{array} $ | (13) |
| $ {A_{mil}}{U_{ki}}{U_{kl}} - {B_m} + {C_{mn}}\left( {{h_n} - {{\bar \lambda }_n}} \right) = 0。$ | (14) |
式中:Mijlk、Maijlk分别为一般、附加质量矩阵,Kijlk1、Knijlk2、Kijlk3分别为材料抗弯刚度、立管张力及曲率、海床弹簧支持力引起的刚度矩阵,Cijlkf为内流引起的阻尼矩阵。
2 模型求解与验证 2.1 静力分析静力分析中,舍弃运动方程中的惯性力项,得:
| $ {R_{il}} = \left( {\mathit{\boldsymbol{K}}_{ijlk}^1 + {{\bar \lambda }_n}\mathit{\boldsymbol{K}}_{nijlk}^2 - \mathit{\boldsymbol{K}}_{ijlk}^3} \right){U_{jk}} - {\mathit{\boldsymbol{F}}_{il}} = 0。$ | (15) |
| $ {G_m} = {A_{mil}}{U_{ki}}{U_{kl}} - {B_m} + {C_{mn}}\left( {{h_n} - {{\bar \lambda }_n}} \right) = 0。$ | (16) |
运用Newton-Raphson法求解非线性方程,假设当前迭代步n未知量估值分别为U(n)、λ(n),应用泰勒级数在估值附近展开,并忽略高阶项,得:
| $ R_{il}^{\left( {n + 1} \right)} = R_{il}^{\left( n \right)} + \frac{{\partial {R_{il}}}}{{\partial {U_{jk}}}}\left( {\Delta {U_{jk}}} \right) + \frac{{\partial {R_{il}}}}{{\partial {\lambda _n}}}\left( {\Delta {\lambda _n}} \right) = 0。$ | (17) |
| $ G_m^{\left( {n + 1} \right)} = G_m^{\left( n \right)} + \frac{{\partial {G_m}}}{{\partial {U_{jk}}}}\left( {\Delta {U_{jk}}} \right) + \frac{{\partial {G_m}}}{{\partial {\lambda _n}}}\left( {\Delta {\lambda _n}} \right) = 0。$ | (18) |
最终矩阵形式如下:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_{ijlk}^{t0\left( n \right)}}&{\mathit{\boldsymbol{K}}_{i\ln }^{t1\left( n \right)}}\\ {\mathit{\boldsymbol{D}}_{mjk}^{t0\left( n \right)} + \mathit{\boldsymbol{D}}_{mn}^{t0\left( n \right)}}&{\mathit{\boldsymbol{D}}_{mn}^{t1\left( n \right)}} \end{array}} \right]\left\{ \begin{array}{l} \Delta {U_{jk}}\\ \Delta {\lambda _n} \end{array} \right\} = \left\{ \begin{array}{l} - R_{il}^{\left( n \right)}\\ - G_m^{\left( n \right)} \end{array} \right\}。$ | (19) |
首先对缓波形立管进行模态分析,忽略立管运动方程中的阻尼力项和荷载项,得:
| $ \left( {{\mathit{\boldsymbol{M}}_{ijlk}} + \mathit{\boldsymbol{M}}_{ijlk}^a} \right){{\ddot U}_{jk}} + \left( {\mathit{\boldsymbol{K}}_{ijlk}^1 + {{\bar \lambda }_n}\mathit{\boldsymbol{K}}_{nijlk}^2 - \mathit{\boldsymbol{K}}_{ijlk}^3} \right){U_{jk}} = 0。$ | (20) |
将方程的解U=φeiωt代入运动方程,得到特征值问题:
| $ \left( {\mathit{\boldsymbol{K}}_{ijlk}^1 + {{\bar \lambda }_n}\mathit{\boldsymbol{K}}_{nijlk}^2 - \mathit{\boldsymbol{K}}_{ijlk}^3} \right)\left\{ \varphi \right\} = {\omega ^2}\left( {{\mathit{\boldsymbol{M}}_{ijlk}} + \mathit{\boldsymbol{M}}_{ijlk}^a} \right)\left\{ \varphi \right\}。$ | (21) |
式中,ω为立管的固有频率;{φ}为相应的模态。
利用时域方法进行缓波形立管在浮体运动等荷载作用下的动力分析,采用预估-校正的Newmark-β法求解运动方程。
(1) 初始条件:以缓波形立管的平衡位形为初始条件,荷载采用斜坡函数从零开始施加。
| $ {u^{\left( 0 \right)}} = 0,{{\dot u}^{\left( 0 \right)}} = 0,{{\ddot u}^{\left( 0 \right)}} = 0。$ | (22) |
(2) 预估:
| $ \begin{array}{l} {{\ddot u}^{\left( n \right)}} = {{\ddot u}^{\left( {n - 1} \right)}},\\ {{\dot u}^{\left( n \right)}} = {{\dot u}^{\left( {n - 1} \right)}} + \Delta t\left( {1 - \gamma } \right){{\ddot u}^{\left( {n - 1} \right)}} + \Delta t\gamma {{\ddot u}^{\left( n \right)}},\\ {u^{\left( n \right)}} = {u^{\left( {n - 1} \right)}} + \Delta t{{\dot u}^{\left( {n - 1} \right)}} + \Delta {t^2}\left( {0.5 - \beta } \right){{\ddot u}^{\left( {n - 1} \right)}} + \\ \;\;\;\;\;\;\;\Delta {t^2}\beta {{\ddot u}^{\left( n \right)}}{\lambda ^{\left( n \right)}} = {\lambda ^{\left( {n - 1} \right)}}。\end{array} $ | (23) |
(3) 计算增量δ(n)={δu(n), δλ(n)}T。
| $ {\delta ^{\left( n \right)}} = {\left[ {{\mathit{\boldsymbol{K}}_T}} \right]^{ - 1}}\left\{ R \right\}。$ | (24) |
式中
(4) 校正:按式(25)对估值进行校正,若增量满足收敛条件则进行下一时间步的计算,否则返回第2步在此时间步内再次进行估值。
| $ \begin{array}{l} {u^{\left( {n + 1} \right)}} = {u^{\left( n \right)}} + \delta {u^{\left( n \right)}},\\ {{\dot u}^{\left( {n + 1} \right)}} = {{\dot u}^{\left( n \right)}} + \frac{\gamma }{{\beta \Delta t}}\delta {u^{\left( n \right)}},\\ {{\ddot u}^{\left( {n + 1} \right)}} = {{\ddot u}^{\left( n \right)}} + \frac{1}{{\beta \Delta {t^2}}}\delta {u^{\left( n \right)}},\\ {\lambda ^{\left( {n + 1} \right)}} = {\lambda ^{\left( n \right)}} + \delta {\lambda ^{\left( n \right)}}。\end{array} $ | (25) |
(5) 重复2~4步,直至完成所有时间步的计算。
基于Matlab平台,将上述静力分析和动力分析的计算过程编制成计算程序LWRNM(Lazy Wave Riser Nonlinear Mechanics)。
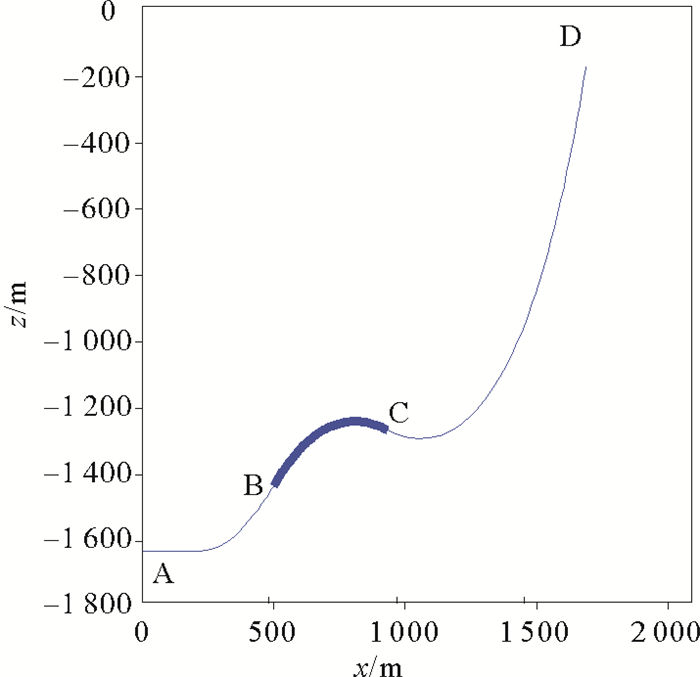
2.3 模型验证选取参考文献[6]的立管参数。立管密度为7 860 kg/m3,弹性模量2.06×1011 Pa,海水密度为1 024 kg/m3,内部流体密度为998 kg/m3, 立管内、外径分别为0.184 1和0.203 2 m,等效浮筒外径0.371 9 m,立管底部长度AB为590 m,浮筒段长度BC为520 m,立管顶部长度CD为1 690 m,顶部偏移1 775 m,水深1 641 m。缓波形立管示意图如图 2。
|
图 2 缓波形立管示意图 Fig. 2 Diagram of lazy wave riser |
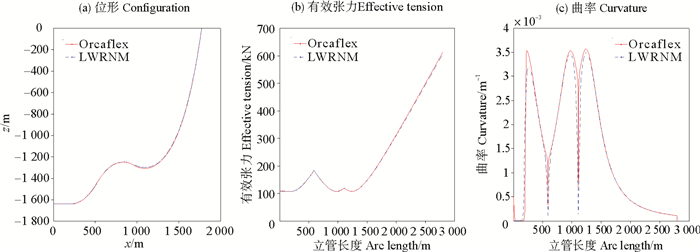
为验证模型的准确性,将本文计算得到的缓波形立管的平衡位形、有效张力和弯曲曲率分别与相同参数条件下商业软件Orcaflex的计算结果进行对比,如图 3所示。由图可知,本文的计算结果与Orcaflex的计算结果吻合较好。
|
图 3 LWRNM与Orcaflex结果比较 Fig. 3 Comparison between LWRNM and Orcaflex |
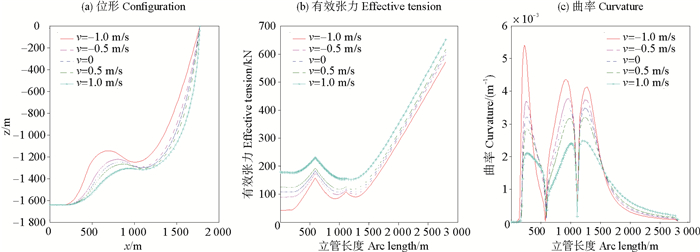
缓波形立管内流密度为998 kg/m3,内流流速为5 m/s。海流流速沿x方向分别取-1.0(负号表示沿x负向)、-0.5、0、0.5、1.0 m/s时,计算缓波形立管的平衡位形、有效张力和弯曲曲率,结果如图 4所示。
|
图 4 不同海流流速下的结构响应 Fig. 4 Structural response with different current velocities |
从图中可以看出,海流对缓波形立管的平衡位形、有效张力和弯曲曲率有很大影响。随着海流方向从x负向变成x正向及海流流速的增加,缓波形立管的线形变缓,有效张力整体增大,弯曲曲率的极值减小。因此,在缓波形立管设计时应该考虑立管所处海域海流的影响。
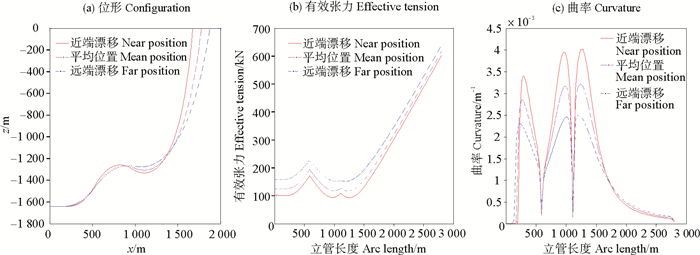
3.1.2 浮体漂移的影响缓波形立管内流密度为998 kg/m3,内流流速为5 m/s,海流流速为0.5 m/s。假设浮体近端和远端漂移位置与其平均位置的距离均为100 m,计算浮体在近端、平均位置和远端时缓波形立管的平衡位形、有效张力和弯曲曲率,结果如图 5所示。
|
图 5 浮体漂移下的结构响应 Fig. 5 Structural response with floating offset |
从图中可以看出,随着顶部浮体从近端向远端漂移,缓波形立管的水平跨距增大,线形变缓,立管有效张力增大,弯曲曲率的极值减小。因此,对缓波形立管进行线形设计时,采用远端漂移的最大张力校核缓波形立管的许用张力,采用近端漂移的最大弯曲曲率校核缓波形立管的最小弯曲半径。
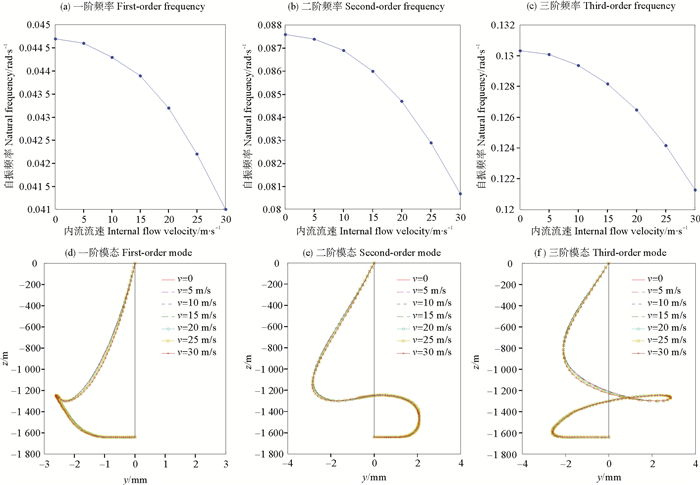
3.2 动力分析 3.2.1 内流的影响本文主要考虑内流对立管动力特性的影响,计算内流密度为998 kg/m3、内流流速分别为0、5、10、15、20、25、30 m/s时立管前3阶固有频率和模态。结果如图 6所示。
|
图 6 不同内流流速下的自振频率和模态 Fig. 6 Natural Frequencies and mode shapes with different internal flow velocities |
从图中可以看出,随着内流流速的增加,缓波形立管的固有频率降低,模态有下沉趋势,这是由于内流流速的增加会引起立管有效张力的减小,进而导致立管刚度Knijlk2的减小,立管固有频率随之减小。虽然实际海洋工程中立管内流的流速不会很高,但随着内流流速的增加,立管的固有频率可能降低到“锁振”频率范围,使得立管产生动力放大,所以立管内流流速对缓波形立管固有频率的影响应引起足够重视。
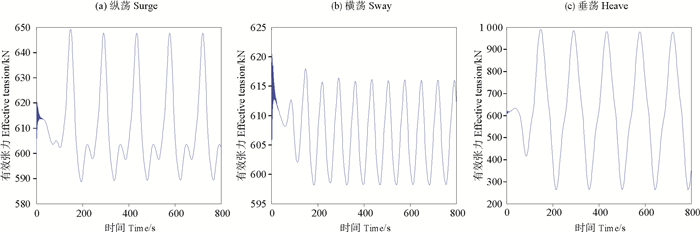
3.2.2 浮体运动计算缓波形立管在浮体运动下的动力响应时,可以将浮体运动看作立管顶端的动边界条件。缓波形立管内流密度为998 kg/m3,内流流速为5 m/s,海流流速为0.5 m/s,顶部浮体以平均位置为中心,做振幅为100 m、周期为143 s的简谐运动,计算缓波形立管在x方向纵荡、y方向横荡和z方向垂荡作用下立管顶部有效张力的时程变化曲线,如图 7所示。
|
图 7 浮体运动下的结构响应 Fig. 7 Structural response with floating motion |
从图中可以看出,缓波形立管顶部张力在初始时间段有一小段振荡,这是由于为消除瞬态响应的影响,外荷载应用斜坡函数从零开始施加,一个荷载周期后达到完整激励值。荷载达到完整激励值后,缓波形立管顶部有效张力呈现周期性变化:纵荡作用下,顶部有效张力稳定变化的最大值为647 kN,分别出现在289、432、575、718 s,时间间隔为143 s,与荷载激励周期相同;横荡作用下,顶部有效张力稳定变化的最大值为615 kN,分别出现在428、500、572、644、716 s,时间间隔为72 s,为荷载激励周期的二分之一;垂荡作用下,顶部有效张力稳定变化的最大值为980 kN,分别出现在433、576、719 s,时间间隔为143 s,变化周期与荷载激励周期相同。垂荡作用下,缓波形立管顶部有效张力变化幅值最大;横荡作用下,缓波形立管顶部有效张力变化幅值最小;纵荡作用下,缓波形立管顶部有效张力变化幅值介于两者之间。
4 结论本文以缓波形立管为研究对象,考虑立管轴向变形和内流作用的影响,采用细长柔性杆模型建立管内流体荷载和管外海洋环境荷载共同作用下缓波形立管的运动方程,运用有限元法求解,编制计算程序LWRNM,对缓波形立管非线性静动力分析,探讨在内流、海流、浮体漂移与运动作用下缓波形立管平衡位形、有效张力和弯曲曲率的变化规律。研究结果表明:
(1)海流对缓波形立管的平衡位形、有效张力和弯曲曲率有很大影响。随着海流方向从x负向变成x正向及海流流速的增大,缓波形立管的线形变缓,有效张力整体增大,弯曲曲率的极值减小。
(2) 随着顶部浮体从近端向远端漂移,缓波形立管的水平跨距增大,线形变缓,立管有效张力增大,弯曲曲率的极值减小。
(3) 随着内流流速的增加,缓波形立管的固有频率降低,模态有下沉趋势。
(4) 缓波形立管顶部有效张力在浮体运动的激励下呈现周期性变化,纵荡和垂荡作用下,顶部有效张力变化周期与激励周期相同;横荡作用下,顶部有效张力变化周期为激励周期的二分之一。垂荡作用下,缓波形立管顶部有效张力变化幅值最大,纵荡作用下次之,横荡作用下最小。
| [1] |
Athisakul C, Klaycham K, Chucheepsakul S. Critical top tension for static equilibrium configuration of a steel catenary riser[J]. China Ocean Engineering, 2014, 28(6): 829-842. DOI:10.1007/s13344-014-0064-x
(  0) 0) |
| [2] |
孟丹, 郭海燕. 深水钢悬链线立管顺流向非线性动力分析[J]. 船舶力学, 2012, 16(1): 127-135. Meng D, Guo H Y. Nonlinear dynamic analysis of deepwater steel catenary riser in-line vibration[J]. Journal of Ship Mechanics, 2012, 16(1): 127-135. DOI:10.3969/j.issn.1007-7294.2012.01.015 (  0) 0) |
| [3] |
Yang H Z, Jiang H, Yang Q. Enhanced multi-layer fatigue-analysis approach for unbonded flexible risers[J]. China Ocean Engineering, 2014, 28(3): 363-379. DOI:10.1007/s13344-014-0029-0
(  0) 0) |
| [4] |
Thomas B, Benirschke A, Sarkar T. Parque das conchas (BC10) steel lazy wave riser installation: Pre-abandonment, recovery and transfer challenges[C]. Offshore Technology Conference. Houston: OTC, 2010.
(  0) 0) |
| [5] |
Li S, Nguyen C. Dynamic response of deepwater lazy-wave catenary riser[C]. DOT-Deep Offshore Technology International Conference. Houston: OTC, 2010.
(  0) 0) |
| [6] |
Wang J, Duan M. A nonlinear model for deepwater steel lazy-wave riser configuration with ocean current and internal flow[J]. Ocean Engineering, 2015, 94: 155-162. DOI:10.1016/j.oceaneng.2014.11.025
(  0) 0) |
| [7] |
孙丽萍, 周佳, 王佳琦. 深水柔性立管的缓波型布置及参数敏感性分析[J]. 中国海洋平台, 2011, 26(3): 37-42. Sun L P, Zhou J, Wang J Q. Lazy wave configuration and parameter sensitivity analysis of deepwater flexible riser[J]. China Offshore Platform, 2011, 26(3): 37-42. DOI:10.3969/j.issn.1001-4500.2011.03.009 (  0) 0) |
| [8] |
李艳, 李欣. 深水缓波形立管的非线性动力分析[J]. 中国造船, 2014, 55(2): 92-101. Li Y, Li X. Nonlinear analysis of lazy-wave steel catenary riser in deepwater[J]. Shipbuilding of China, 2014, 55(2): 92-101. DOI:10.3969/j.issn.1000-4882.2014.02.011 (  0) 0) |
| [9] |
宋磊建, 韩芸, 付世晓, 等. 深水缓波形脐带缆结构响应及参数敏感性分析[J]. 振动与冲击, 2015(19): 109-114. Song L J, Han Y, Fu S X, et al. Structural responses and parameter sensitivity analysis of a lazy-wave deepwater umbilical[J]. Journal of Vibration and Shock, 2015(19): 109-114. (  0) 0) |
| [10] |
Orcina Ltd. OrcaFlex Manual Version 10.0a[M]. UK: Orcina Ltd, 2015.
(  0) 0) |
| [11] |
Garrett D L. Dynamic analysis of slender rods[J]. Journal of Energy Resources Technology, 1982, 104: 302-306. DOI:10.1115/1.3230419
(  0) 0) |
| [12] |
陈海飞.深水柔性立管非线性静动力分析[D].青岛: 中国海洋大学, 2011. Chen H F.Nonlinear Static and Dynamic Analyses of Deepwater Flexible Risers[D]. Qingdao: Ocean University of China, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011229137.htm (  0) 0) |
| [13] |
Paidoussis M P. Fluid-Structure Interactions: Slender Structures and Axial Flow[M]. London: Academic Press, 1998: 71-76.
(  0) 0) |
2. Jangsu Universits of Science and Technologs, School of Nawal Architecture & Ocean Engineering, Zhenjiang 212003, China
 2019, Vol. 49
2019, Vol. 49


