著名的Poincaré-Birkhoff定理和它的推广形式是研究平面保守系统周期解问题的有力工具[1-7]。但是,平面耗散系统对应的Poincaré映射一般不满足保面积条件,因此,Poincaré-Birkhoff定理通常不能用来研究其周期解问题。针对这种情况,丁同仁[8-9]建立了不需要保面积条件,代之以某种弯曲条件的新的解析扭转映射不动点定理,并利用它证明了耗散Duffing方程
| $ x^{\prime \prime}+\varepsilon c x^{\prime}+\left(a x+b x^3\right)=E p(t) $ |
至少有两个不同的k阶次调和解,条件是只要ε>0和E>0充分小。
马如云等[10]利用集连通理论,给出了非保面积的扭转映射至少有两个不动点的一个新定理。Pascoletti和Zanolin[11]通过拓扑方法推广了丁同仁[8]的扭转弯曲定理,并得到了一些新的带有弯曲条件的不动点定理。作为应用,作者证明了如下结果:当ε>0充分小,w(t)为非负的周期函数时,方程
| $ x^{\prime \prime}+\varepsilon x^{\prime}+(1+w(t)) f(x)=0 $ |
至少有四个初值在一星形环域中的次调和解。
本文的目的是拓展弯曲扭转映射定理的应用范围, 利用文献[11]的一个抽象结论,即下文中的引理4,来研究双项位势Duffing方程
| $ x^{\prime \prime}+\varepsilon x^{\prime}+a(t) f(x)+b(t) g(x)=0 $ | (1) |
的周期解问题,其中a(t), b(t)是连续的T-周期函数。
1 准备假设a, b: R→R是T-周期连续函数。对于以T为周期的周期函数α(t), 记其平均值
(H0) f(0)=0, g(0)=0, 且存在常数N*>0使得
| $ 0<\frac{f(x)}{x}, \frac{g(x)}{x} \leqslant N^*, \quad \forall x \in I \backslash\{0\} 。$ |
(H1) 存在常数δ0>0, 满足
| $ \begin{gathered} \hat{a}(t)=\hat{b}(t)=0, \quad t \in\left[0, T-\delta_0\right], \\ \hat{a}(t) \geqslant 0, \hat{b}(t) \geqslant 0, \hat{a}^2(t)+\hat{b}^2(t) \neq 0, t \in\left(T-\delta_0, T\right) 。\end{gathered} $ |
(H2) 存在常数δ0>0, 满足
| $ x^{\prime \prime}+a(t) f(x)+b(t) g(x)=0 \text { 。} $ | (2) |
方程(2)可写成
| $ x^{\prime \prime}+\bar{a} f(x)+\bar{b} g(x)+\hat{a}(t) f(x)+\hat{b}(t) g(x)=0, $ | (3) |
其等价系统为
| $ \left\{\begin{array}{l} x^{\prime}=y, \\ y^{\prime}=-\bar{a} f(x)-\bar{b} g(x)-\hat{a}(t) f(x)-\hat{b}(t) g(x) 。\end{array}\right. $ | (4) |
考虑辅助方程
| $ x^{\prime \prime}+\bar{a} f(x)+\bar{b} g(x)=0 $ | (5) |
及其等价系统
| $ \left\{\begin{array}{l} x^{\prime}=y, \\ y^{\prime}=-\bar{a} f(x)-\bar{b} g(x) 。\end{array}\right. $ | (6) |
我们将系统(4)看作是系统(6)的扰动系统。
令ϕ(·)=ϕ(·, z)表示系统(6)满足初值条件ϕ(0)=z的解。计算得系统(6)的首次积分为
| $ E(x, y):=\frac{1}{2} y^2+\bar{a} F(x)+\bar{b} G(x)=c, $ | (7) |
其中,
令τ(c)表示Ec的最小正周期,则τ(c)是关于c的连续函数(参见[11])。引入假设:
(H3) 存在常数c1, c2: 0 < c1 < c2 < C使得,对于任意常数ε*>0, 有0 < c2-c1 < ε*, 并且T介于τ(c1)和τ(c2)之间。
令A={(x, y)∈I×R: c1≤E(x, y)≤c2}, 则A是平面上的一个环域,其内外边界分别为Ec1和Ec2。
令Lθ表示所有极角为θ的点的集合,则Lθ与Ec有且只有一个交点。因此,可以引入一个与极坐标投影映射等价的覆盖映射Ξ: A→R2, 使得
| $ \mathit{\Xi }(x, y) = (\theta , \xi ), \quad (x, y) \in A, $ |
式中: θ是通常意义下的极角,ξ=E(x, y)。
现在我们可以叙述本文的主要结果。
定理1
假设条件(H0), (H3)成立,且条件(H1)或(H2)成立,则存在充分小的正常数δ, 使得当
将条件(H1), (H2)做一些弱化。假设存在正常数
(H1)*存在常数δ0>0, 满足
| $ \begin{gathered} \breve{a}(t)=\breve{b}(t)=0, \quad t \in\left[0, T-\delta_0\right], \\ \breve{a}(t) \geqslant 0, \breve{b}(t) \geqslant 0, \breve{a}^2(t)+\breve{b}^2(t) \neq 0, t \in\left(T-\delta_0, T\right) ; \end{gathered} $ |
(H2)*存在常数δ0>0, 满足
| $ \begin{gathered} \breve{a}(t)=\breve{b}(t)=0, \quad t \in\left[0, T-\delta_0\right], \\ \breve{a}(t) \leqslant 0, \breve{b}(t) \leqslant 0, \breve{a}^2(t)+\breve{b}^2(t) \neq 0, t \in\left(T-\delta_0, T\right)。\end{gathered} $ |
我们可以得到稍微宽泛的结果。
定理2 假设条件(H0), (H3)成立, 且存在正常数
注1 因为条件(H1)或(H2) ((H1)*或(H2)*)不排除a(t)和b(t)在一个周期内变号,因此上述两定理适用范围比文献[11]中的相应结论更广泛。我们将在本文最后举例说明这一点。
2 主要结果的证明设X⊂R2是一个拓扑环,h: X→R2\{0}是一个连续映射,记Xi和Xo分别是X的内外边界,所围的区域分别是
| $ \mathit{\Pi }:(\varphi , r) \to (r\cos \varphi , r\sin \varphi ) $ |
为标准覆盖映射,则由覆盖投射理论[12]可知,h存在一个连续的提升映射
| $ \widetilde{h}:(\varphi, r) \rightarrow\left(\varphi+g^*(\varphi, r), r^*(\varphi, r)\right), $ |
满足
下面的引理来自文献[11]中的推论2.10, 它是我们证明主要定理的基本工具。
引理1 假设
(A1)h的提升映射
| $ \left\{\begin{array}{l} g^*(\varphi, r)>2 j \pi(<2 j \pi), (r \cos \varphi, r \sin \varphi) \in X_i, \\ g^*(\varphi, r)<2 j \pi(>2 j \pi), (r \cos \varphi, r \sin \varphi) \in X_o, \end{array}\right. $ |
式中j是给定的整数。
(A2)X中存在2k个连接Xi和Xo且互不相交的曲线, 分别用Γ1, Γ2, …,Γn, …,Γ2k, Γ2k+1=Γ1进行标记,满足
| $ \left\{\begin{array}{l} Y(z)<0, z \in \Gamma_{2 n-1}, n=1, 2, \cdots, k ; \\ Y(z)>0, z \in \Gamma_{2 n}, n=1, 2, \cdots, k 。\end{array}\right. $ |
式中Y(z)=r*(φ, r)-r。则映射h在X的内部intX至少有2k个不同的不动点。
注2 由文献[11]中的论述可知,我们可以将Y表示为Y(z)=E(h(z))-E(z)。
下面我们进行定理1的证明。
证明 我们不妨假设τ(c1) < T < τ(c2)。由于τ(c)连续,因此系统(6)至少有一个T-周期解φ(t)=(x(t), y(t)), 满足
令
| $ D=\left\{(x, y) \in I \times \bf{R}: E(x, y) \leqslant c_2\right\} \text { 。} $ |
因
| $ {\psi _{\hat a, \hat b}}(t, z) \ne 0, \quad \forall t \in [0, T], z \in A 。$ |
定义函数
| $ {\psi _{\hat a, \hat b}}(t, z) = \left\| {{\psi _{\hat a, \hat b}}(t, z)} \right\|(\cos (\vartheta (t, z)), \sin (\vartheta (t, z)))。$ |
令
| $ {\mathit{\widetilde \Psi }_{\hat a, \hat b}}(\theta , \xi ) = \left( {\theta + {\mathit{\Theta }_{\hat a, \hat b}}(\theta , \xi ), {\xi ^*}} \right), $ |
式中:θ是通常的极角;ξ=E(x, y)。
对于z=(ξcosθ, ξsinθ), 有
| $ {\xi ^*} = \left\| {{\mathit{\Psi }_{\hat a, \hat b}}(z)} \right\|, $ | (8) |
| $ {\mathit{\Theta }_{\hat a, \hat b}}(\theta , \xi ) = \int_0^T {\frac{{\left[ {\bar af\left( {{\psi _1}(t, z)} \right) + \bar bg\left( {{\psi _1}(t, z)} \right) + \hat a(t)f\left( {{\psi _1}(t, z)} \right) + \hat b(t)g\left( {{\psi _1}(t, z)} \right)} \right]{\psi _1}(t, z) + {\psi _2}{{(t, z)}^2}}}{{{{\left\| {{\psi _{\hat a, \hat b}}(t, z)} \right\|}^2}}}} {\rm{d}}t 。$ | (9) |
显然,在L1拓扑下映射
| $ {\mathit{\Theta }_{0, 0}}(\theta , \xi ) = - 2\pi , \quad (\theta , \xi ) \in {E^{\hat c}}。$ | (10) |
由于系统(6)从Ec出发的解绕原点顺时针旋转,且τ(c1) < T < τ(c2), 故
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\Theta }_{0, 0}}(\theta , \xi ) < - 2\pi , }&{(\theta , \xi ) \in {E^{{c_1}}}, }\\ {{\mathit{\Theta }_{0, 0}}(\theta , \xi ) > - 2\pi , }&{(\theta , \xi ) \in {E^{{c_2}}}}。\end{array}} \right. $ | (11) |
因此,结合公式(9)可得,存在常数δ>0,使得当
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\Theta }_{\hat a, \hat b}}(\theta , \xi ) < - 2\pi , (\theta , \xi ) \in {E^{c1}}, }\\ {{\mathit{\Theta }_{\hat a, \hat b}}(\theta , \xi ) > - 2\pi , (\theta , \xi ) \in {E^{c2}}}。\end{array}} \right. $ | (12) |
即
下面证明A中存在4条连接Ec1和Ec2的曲线Γ1, Γ2, Γ3, Γ4, 且满足引理1中的条件(A2)。
假设条件(H1)成立(条件(H2)成立时可类似证明)。令
| $ {Y_{\hat a, \hat b}}(z) = E\left( {{\mathit{\Psi }_{\hat a, \hat b}}(z)} \right) - E(z), \quad \forall z \in A 。$ |
根据E(x, y)的定义,可以得到
| $ \begin{aligned} & \frac{\mathrm{d}}{\mathrm{d} t} E\left(\psi_a, \hat{b}(t, z)\right)=\frac{\mathrm{d}}{\mathrm{d} t} E\left(\psi_1(t, z), \psi_2(t, z)\right)= \\ & \psi_2(t, z) \psi_2^{\prime}(t, z)+\bar{a} f\left(\psi_1(t, z)\right) \psi_1^{\prime}(t, z)+ \\ & \bar{b} g\left(\psi_1(t, z)\right) \psi_1^{\prime}(t, z)= \\ & \psi_2(t, z)\left[-\bar{a} f\left(\psi_1(t, z)\right)-\bar{b} g\left(\psi_1(t, z)\right)-\right. \\ & \left.\hat{a}(t) f\left(\psi_1(t, z)\right)-\hat{b}(t) g\left(\psi_1(t, z)\right)\right]+ \\ & \bar{a} f\left(\psi_1(t, z)\right) \psi_2(t, z)+\bar{b} g\left(\psi_1(t, z)\right) \psi_2(t, z)= \\ & \psi_2(t, z)\left[-\hat{a}(t) f\left(\psi_1(t, z)\right)-\hat{b}(t) g\left(\psi_1(t, z)\right)\right] 。\end{aligned} $ | (13) |
由条件(H0), (H1)可知,对任意t∈(T-δ0, T), 有
| $ \begin{aligned} & \frac{\mathrm{d}}{\mathrm{d} t} E\left(\psi_{a, b}(t, z)\right)>0, \psi_{a, b}(t, z) \in \mathfrak{D}_1, \\ & \frac{\mathrm{d}}{\mathrm{d} t} E\left(\psi_{a, b}(t, z)\right)<0, \psi_{\hat{a}, b}(t, z) \in \mathfrak{D}_2, \end{aligned} $ | (14) |
式中:
令
| $ E\left( {{\mathit{\Psi }_{\hat a, \hat b}}(z)} \right) = E\left( {{\psi _{\hat a, \hat b}}(T, z)} \right) < E\left( {{\psi _{\hat a, \hat b}}\left( {T - {\delta _0}, z} \right)} \right)。$ |
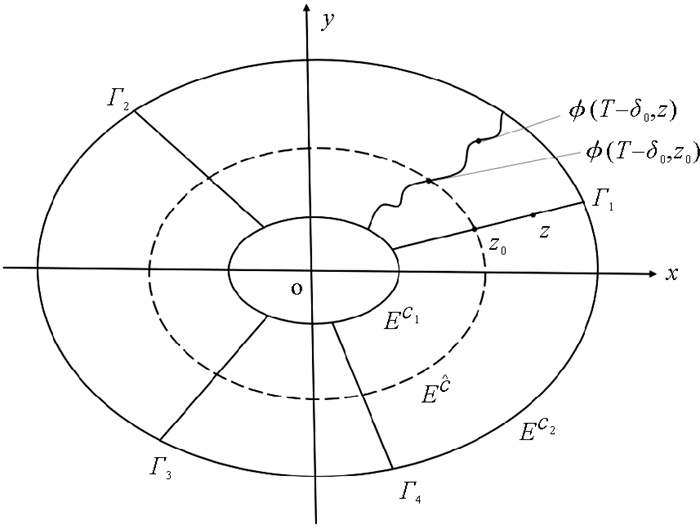
|
图 1 公式(6)的周期轨迹 Fig. 1 The periodic orbits of the formula (6) |
由条件(H1)可知,对于t∈[0, T-δ0],系统(4)和(6)的解重合,从而
| $ E\left( {{\psi _{\hat a, \hat b}}\left( {T - {\delta _0}, z} \right)} \right) = E\left( {\varphi \left( {T - {\delta _0}, z} \right)} \right) = E(z), $ |
从而
| $ E\left( {{\mathit{\Psi }_{\hat a, \hat b}}(z)} \right) - E(z) < 0, \quad \forall z \in {\mathit{\Gamma }_1}。$ | (15) |
利用类似的方法, 我们还可以得到
| $ \begin{array}{*{20}{l}} {E\left( {{\mathit{\Psi }_{\hat a, \hat b}}(z)} \right) - E(z) > 0, }&{z \in {\mathit{\Gamma }_2}: = {L_{\pi - \alpha }} \cap A, }\\ {E\left( {{\mathit{\Psi }_{\hat a, \hat b}}(z)} \right) - E(z) < 0, }&{z \in {\mathit{\Gamma }_3}: = {L_{\frac{3}{2}\pi - \alpha }} \cap A, }\\ {E\left( {{\mathit{\Psi }_{\hat a, \hat b}}(z)} \right) - E(z) > 0, }&{z \in {\mathit{\Gamma }_4}: = {L_{2\pi - \alpha }} \cap A, } \end{array} $ |
即
| $ \left\{ {\begin{array}{*{20}{l}} {{Y_{\hat a, \hat b}}(z) < 0, z \in {\mathit{\Gamma }_1}, {\mathit{\Gamma }_3}, }\\ {{Y_{\hat a, \hat b}}(z) > 0, z \in {\mathit{\Gamma }_2}, {\mathit{\Gamma }_4}。} \end{array}} \right. $ | (16) |
因此, 由引理1可知, 存在常数δ>0使得当
| $ {\mathit{\Theta }_{\hat a, \hat b}}(0, \theta , \xi ) = {\mathit{\Theta }_{\hat a, \hat b}}(\theta , \xi ), {\mathit{\Upsilon }_{\hat a, \hat b}}(0, z) = {\mathit{\Upsilon }_{\hat a, \hat b}}(z)。$ |
由
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\Theta }_{\hat a, \hat b}}(\varepsilon , \theta , \xi ) < - 2\pi , (\theta , \xi ) \in {E^{c1}}}, \\ {{\mathit{\Theta }_{\hat a, \hat b}}(\varepsilon , \theta , \xi ) > - 2\pi , (\theta , \xi ) \in {E^{c2}}}, \end{array}} \right. $ |
且
| $ \left\{ {\begin{array}{*{20}{l}} {{Y_{\hat a, \hat b}}(\varepsilon , z) < 0, z \in {\mathit{\Gamma }_1}, {\mathit{\Gamma }_3}, }\\ {{Y_{\hat a, \hat b}}(\varepsilon , z) > 0, z \in {\mathit{\Gamma }_2}, {\mathit{\Gamma }_4}。} \end{array}} \right. $ |
因此公式(1)也至少有4个初值在A中的T-周期解。
定理1证毕。
注3 定理2的证明类似于定理1,只需要将证明过程中的a, b分别换成
下面举例说明定理2的有效性。
例1 考虑方程
| $ x^{\prime \prime}+\frac{1}{n} x^{\prime}+a(t) f(x)+b(t) g(x)=0, $ | (17) |
式中:n是正整数;a(t), b(t)是
| $ a(t)= \begin{cases}1, & t \in\left[0, \sqrt{2} \pi-\frac{1}{n}\right], \\ 4\left(n^2+n\right) t^2+(n+1)(4-8 \sqrt{2} n \pi) t+(n+1)\left(8 n \pi^2-4 \sqrt{2} \pi\right)+1, & t \in\left(\sqrt{2} \pi-\frac{1}{n}, \sqrt{2} \pi\right), \end{cases} $ |
| $ b(t)= \begin{cases}1, & t \in\left[0, \sqrt{2} \pi-\frac{1}{n}\right], \\ -2(n+1) t+2\left(\sqrt{2} \pi-\frac{1}{n}\right)(n+1)+1, & t \in\left(\sqrt{2} \pi-\frac{1}{n}, \sqrt{2} \pi-\frac{1}{2 n}\right], \\ 2(n+1) t-2 \sqrt{2} \pi(n+1)+1, & t \in\left(\sqrt{2} \pi-\frac{1}{2 n}, \sqrt{2} \pi\right), \end{cases} $ |
取
| $ \begin{aligned} & \breve{a}(t)=a(t)-\widetilde{a}=a(t)-1=0, t \in\left[0, T-\delta_0\right], \\ & \breve{b}(t)=b(t)-\widetilde{b}=b(t)-1=0, t \in\left[0, T-\delta_0\right] 。\end{aligned} $ |
从而,条件(H2)*成立。
计算可得
| $ \begin{array}{l} \ \ \ \ {\left\| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} } \right\|_1} = \int_0^{\sqrt 2 \pi } | a(t) - \tilde a|{\rm{d}}t = \\ \int_{\sqrt 2 \pi - {\delta _0}}^{\sqrt 2 \pi } {(\tilde a - a(} t)){\rm{d}}t = \widetilde a{\delta _0} + \int_{\sqrt 2 \pi - {\delta _0}}^{\sqrt 2 \pi } {( - a(} t)){\rm{d}}t = \\ \frac{4}{3}(n + 1)\left( { - 6{\pi ^2} + 3\sqrt 2 \pi {\delta _0} - \delta _0^2} \right) + (n + 1)\left( {2\delta _0^2 - } \right.\\ \left. {4\sqrt 2 n\pi \delta _0^2 + 8n{\pi ^2}{\delta _0}} \right) = \frac{2}{{3{n^2}}}(n + 1)。\end{array} $ |
| $ \begin{array}{l} \ \ \ \ \|\bar{b}\|_1=\int_0^{\sqrt{2} \pi}|b(t)-\widetilde{b}| \mathrm{d} t= \\ \int_{\sqrt{2} \pi-\delta_0}^{\sqrt{2} \pi}(\widetilde{b}-b(t)) \mathrm{d} t=\widetilde{b} \delta_0+\int_{\sqrt{2} \pi \delta_0}^{\sqrt{2} \pi}(-b(t)) \mathrm{d} t= \\ \widetilde{b}_0+\int_{\sqrt{2} \pi-\frac{1}{n}}^{\sqrt{2} \pi-\frac{1}{2 n}}\left[-2(n+1) t+2\left(\sqrt{2} \pi-\frac{1}{n}\right)(n+1)+1\right] \mathrm{d} t+ \\ \int_{\sqrt{2} \pi-\frac{1}{2 n}}^{\sqrt{2} \pi}[2(n+1) t-2 \sqrt{2} \pi(n+1)+1] \mathrm{d} t= \\ (n+1)\left(\frac{3}{4 n^2}-\frac{\sqrt{2} \pi}{n}\right)+(n+1) \frac{1}{n}\left(\sqrt{2} \pi-\frac{1}{n}\right)- \\ \frac{n+1}{4 n^2}+\frac{2}{n}=\frac{3}{2 n}-\frac{1}{2 n^2} 。\end{array} $ |
因此,
f, g∶(-1, 1)→R定义如下:f(0)=g(0)=0, f(x), g(x)为奇函数,且
| $ \begin{aligned} & f(x)=x\left(\frac{4}{5} \cos (\ln x)+1\right), x \in(0, 1), \\ & g(x)=x\left(1-\frac{2}{5} \sin (\ln x)\right), x \in(0, 1) 。\end{aligned} $ |
则
| $ \begin{aligned} & f^{\prime}(x)=\frac{4}{5} \cos (\ln x)-\frac{4}{5} \sin (\ln x)+1, x \in(0, 1), \\ & g^{\prime}(x)=1-\frac{2}{5} \sin (\ln x)-\frac{2}{5} \cos (\ln x), x \in(0, 1) 。\end{aligned} $ |
从而,f′(x), g′(x)在(0, 1)上有界。因此,f(x), g(x)满足局部Lipschitz条件。且容易验证f(x), g(x)满足条件(H0)。
当x∈(0, 1)时,方程
| $ E(x, y)=\frac{1}{2} y^2+H(x)=c, $ |
其中,
| $ H(x)=x^2\left(1+\frac{2}{5} \cos (\ln x)\right) \text { 。} $ |
令
| $ \begin{array}{l} \ \ \ \ \tau (c) = 2\sqrt 2 \int_0^{{h_c}} {\frac{{{\rm{d}}u}}{{\sqrt {c - H(u)} }}} = \\ 2\sqrt 2 \int_0^1 {\frac{{{h_c}{\rm{d}}\sigma }}{{\sqrt {H\left( {{h_c}} \right) - H\left( {{h_c}\sigma } \right)} }}} = \\ \frac{{2\sqrt 2 }}{{\sqrt {Q\left( {{h_c}} \right)} }}\int_0^1 {\frac{{{\rm{d}}\sigma }}{{\sqrt {1 - {\sigma ^2}Q\left( {{h_c}\sigma } \right)/Q\left( {{h_c}} \right)} }}} \end{array} $ | (18) |
下面证明τ(c)满足条件。
由于
| $ c_1^*=H\left(\mathrm{e}^{-3 \pi}\right), c_2^*=H\left(\mathrm{e}^{-2 \pi}\right) \text { 。} $ |
由于
| $ 0<\mathrm{e}^{-3 \pi}<\mathrm{e}^{-2 \pi}<1 $ |
则
| $ \begin{aligned} \tau\left(c_1^*\right) & =\frac{2 \sqrt{2}}{\sqrt{Q\left(\mathrm{e}^{-3 \pi}\right)}} \int_0^1 \frac{\mathrm{d} \sigma}{\sqrt{1-\sigma^2 Q\left(\mathrm{e}^{-3 \pi} \sigma\right) / Q\left(\mathrm{e}^{-3 \pi}\right)}}>\sqrt{2} \pi, \\ \tau\left(c_2^*\right) & =\frac{2 \sqrt{2}}{\sqrt{Q\left(\mathrm{e}^{-2 \pi}\right)}} \int_0^1 \frac{\mathrm{d} \sigma}{\sqrt{1-\sigma^2 Q\left(\mathrm{e}^{-2 \pi} \sigma\right) / Q\left(\mathrm{e}^{-2 \pi}\right)}}<\sqrt{2} \pi 。\end{aligned} $ |
因此,由函数τ(c)的连续性可知,存在正常数c1, c2, c*∶ c1* < c1 < c* < c2 < c2*, 满足对于任意常数ε*>0, 有0 < c2-c1 < ε*, 且τ(c*)=2π介于τ(c1)与τ(c2)之间。从而条件(H3)成立。
因
| [1] |
Ding T R. An infinite class of periodic solutions of periodically perturbed Duffing equations at resonance[J]. Proceedings of the American Mathematical Society, 1982, 86(1): 47-54. DOI:10.1090/S0002-9939-1982-0663864-1 (  0) 0) |
| [2] |
Ding T R, Ding W Y. Resonance problem for a class of Duffing's equations[J]. Chinese Annals of Mathematics, 1985, 6(4): 427-432. (  0) 0) |
| [3] |
Hao D Y, Ma S W. Semilinear Duffing equations crossing resonance points[J]. Journal of Differential Equations, 1997, 133(1): 98-116. DOI:10.1006/jdeq.1996.3193 (  0) 0) |
| [4] |
Jacobowitz H. Periodic solutions of x″+f(x, t)=0 via the Poincaré-Birkhoff theorem[J]. Journal of Differential Equations, 1976, 20(1): 37-52. DOI:10.1016/0022-0396(76)90094-2 (  0) 0) |
| [5] |
Leach D E. On PoincarÃ's perturbation theorem and a theorem of W. S. Loud[J]. Journal of Differential Equations, 1970, 7(1): 34-53. DOI:10.1016/0022-0396(70)90122-1 (  0) 0) |
| [6] |
Mawhin J. Contractive mappings and periodically perturbed conservaive systems[J]. Archivum Mathematicum, 1976, 12(2): 67-73. (  0) 0) |
| [7] |
Wang Z H. Periodic solutions of the second order differential equations with Lipschitzian condition[J]. Proceedings of the American Mathematical Society, 1998, 126(8): 2267-2276. DOI:10.1090/S0002-9939-98-04772-8 (  0) 0) |
| [8] |
丁同仁. 扭转弯曲定理和它的一个应用[J]. 数学进展, 2012, 41(1): 31-44. Ding T R. The twist-bend theorem with an application[J]. Advances in Mathematics, 2012, 41(1): 31-44. (  0) 0) |
| [9] |
Ding T R. Approaches to the Qualitative Theory of Ordinary Differential Equations[M]. Singapore: World Scientific Publishing Company, 2007.
(  0) 0) |
| [10] |
马如云, 伏升茂, 李战存. 扭转映射的一个不动点定理[J]. 数学研究与评论, 1996, 16(3): 452-454. Ma R Y, Fu S M, Li Z C. A fixed points theorem for twist maps[J]. Journal of Mathematical Research and Exposition, 1996, 16(3): 452-454. (  0) 0) |
| [11] |
Pascoletti A, Zanolin F. A topological approach to bend-twist maps with applications[J]. International Journal of Dynamical Systems and Differential Equation, 2011, 2011: 1-20. (  0) 0) |
| [12] |
Joo B P. Lectures on algebraic topology[J]. Bulletin of the Brazilian Mathematical Society, 1971, 2(1): 63-66. DOI:10.1007/BF02584807 (  0) 0) |
| [13] |
张芷芬, 丁同仁, 黄文灶. 微分方程定性理论[M]. 北京: 科学出版社, 1985. Zhang Z F, Ding T R, Huang W Z. Qualitative Theory of the Differential Equations[M]. Beijing: Science Press, 1985. (  0) 0) |
 2023, Vol. 53
2023, Vol. 53

