2. 天津大学天津市港口与海洋工程重点实验室, 天津 300072;
3. 北部湾大学机械与船舶海洋工程学院, 广西 钦州 535011
目前,随着国家的快速发展和对能源需求的不断增加,加速开发海洋油气资源已经成为未来国家能源战略的重中之重[1]。管道是运输石油、天然气极为安全和最具成本效益的方式,确保其整体结构的安全性和完整性至关重要。
在海底管道安全服役期间,结构失效的主要原因之一就是结构性能的降低[2]。一方面,与陆地结构相比,海底管道结构表面可能遭受严重的腐蚀损伤,在其表面产生蚀坑进而降低材料力学性能[3];另一方面,作用在结构上的循环载荷会导致结构的疲劳破坏,而腐蚀疲劳就是腐蚀环境与循环载荷相耦合作用下的结果,其造成结构的损坏程度可能比二者单独作用的总和还要大[4]。也就是说,海底管道的疲劳可靠性需要有更高的要求,这些要求可以从船级社的一些设计规则中得到很好的证明[5-6]。深入研究腐蚀疲劳是构件安全设计的基础,也是构件剩余寿命预测的依据。
对于腐蚀疲劳裂纹扩展问题,学者们展开了诸多研究。Dong-Hwan Kang等[7]研究了高强钢HSB800在空气和海水环境下的疲劳和腐蚀疲劳裂纹扩展行为基于Paris公式和Forman方程提出了一种基于力学的腐蚀疲劳裂纹扩展预测断裂模型Ankang Cheng和Nian-Zhong Chen[8]从工程批判性评估(ECA)的角度提出了一种基于腐蚀—裂纹关联模型的临界应力强度因子(SIF)计算公式;杨斌等[9]对2205双相不锈钢(DSS)分别在空气、去离子水和3.5%NaCl溶液中进行疲劳裂纹扩展试验,得出氢致开裂导致该材料的疲劳性能弱化,去离子水裂纹扩展速率高于NaCl溶液,空气中材料疲劳裂纹扩展寿命最高的结论。Tianliang Zhao等[10-11]针对E690钢,通过腐蚀疲劳试验,得出当峰值应力接近或高于材料屈服应力时,裂纹由出现的腐蚀坑处萌生;还基于腐蚀动力学和等效初始裂纹尺寸理论建立了腐蚀疲劳寿命评估模型,但评估模型仍难以适用于低峰值应力的情况。Danyil Kovalov等[12]建立了一种通用腐蚀疲劳模型,用于预测金属在循环载荷作用下的腐蚀疲劳裂纹扩展速率。
目前国内外有大量关于疲劳裂纹扩展特性的研究[13-15],由于腐蚀疲劳裂纹扩展特性的研究增加了腐蚀环境,研究内容更为复杂,其成果相对较少,大体上侧重于从软件模拟和断裂力学的角度对腐蚀疲劳裂纹扩展特性进行研究[16-17];对于深海管道常用材料X65钢而言,关于腐蚀疲劳裂纹扩展特性的相关研究几乎空白。而在中国深海石油工程中,X65钢作为常用钢种,服役过程中将承受海水腐蚀和外界疲劳载荷的共同作用,其腐蚀疲劳裂纹扩展性能需要更为明确深入的研究。本文采用了可控制疲劳裂纹扩展路径的侧壁开槽技术,对标准CT试样进行改进,通过对试样应力强度因子的有限元计算结果与理论计算结果对比,验证了侧壁开槽型CT试样应力强度因子理论解;分别在腐蚀溶液和空气中进行裂纹扩展试验,对裂纹扩展的稳定阶段采用Paris公式对da/dN与ΔK的关系进行分析处理,获得腐蚀环境对X65钢裂纹扩展特性的影响。
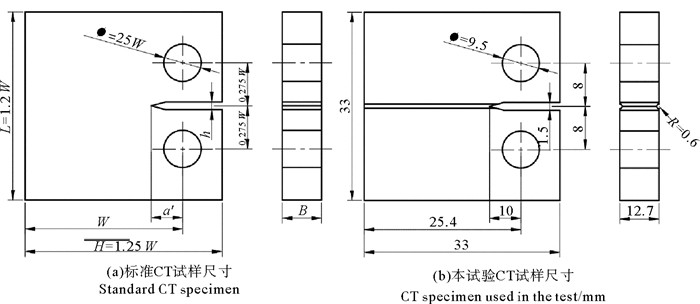
1 侧壁开槽型CT试样应力强度因子计算 1.1 试样尺寸及材料属性疲劳裂纹扩展试验常用的试样形式为标准CT试样,如图 1(a)所示,ASTM在E647-15[18]对疲劳裂纹扩展的标准CT试样形式给出了相关规定。同时,为保证试样既能满足腐蚀疲劳试验机的夹具要求,又可控制裂纹扩展方向,对标准CT试样采用侧壁开槽技术以实现裂纹以直线形式扩展。侧壁开槽技术是一种提高试件裂纹均匀稳定扩展的技术[18]。侧壁开槽增加了裂纹尖端的约束,从而可实现裂纹以直线形式扩展,BS 8571:2014[20]表明试样采用该方法是可取的。最终本文所采用的CT试样及尺寸如图 1(b)所示,与标准CT试样不同,试样添加R=0.6 mm的槽口,最大高度H和最大长度L均设置为33 mm,装夹孔直径Ф=9.5 mm。
|
图 1 标准CT试样与本试验CT试样尺寸图 Fig. 1 Different size of the standard CT specimen and the CT specimen used in the test |
本文采取的CT试样材料为管道用钢X65,X65的化学成分质量分数为0.09%C、1.51%Mn、0.30%Si、0.024%P、0.002%S、0.019%Ni、0.031%Cr、0.003%Mo、0.060%Nb、0.005%V、0.05%Ti,其余为Fe。经试验测得的材料属性见表 1。
|
|
表 1 qX65力学性能参数 Table 1 The mechanical properties of X65 |
为了验证ASTM标准中提出的应力强度因子计算公式对本文试验采用的CT试样的适用性,利用ABAQUS有限元软件中的围线积分法,在拉伸载荷作用下,采用三维模型直线型裂纹形貌,对不同尺寸CT试样在弹性范围内的裂纹尖端应力强度因子展开数值分析。
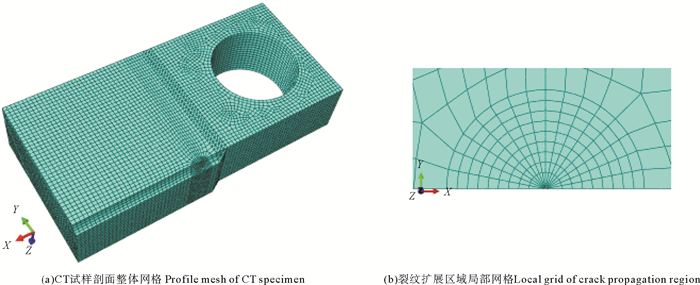
1.2.1 基于ABAQUS的三维CT试样几何模型建模利用ABAQUS软件按图 1(b)的尺寸进行建模。在有限元建模过程中,CT试样的几何特征、载荷施加和边界约束条件都具有一定的对称性,故采取模型的1/4进行分析。网格划分过程中,选择C3D20R网格单元,设置合适的网格密度,如图 2(a)所示。本文将构件剖分,对裂纹扩展区进行足够的剖分,以便保证构件各部分采用较合理的网格划分方式,如图 2(b)所示。
|
图 2 网格划分示意图 Fig. 2 Schematic diagram of grid division |
由于采用1/4模型,在试样的两个对称面施加对称边界约束;对加载孔的中心位置,施加X方向位移为零的约束;基于模型的对称性,施加于试样上的载荷也设置为试验最大值的一半,即12 kN,方向沿Y轴正向。
1.2.2 不同尺寸CT试样裂纹应力强度因子分析标准紧凑拉伸试样的应力强度因子表达式[21]如下:
| $ \begin{array}{l} K=\frac{P}{\sqrt{B B_{N}} \sqrt{W}} \frac{2+\alpha}{(1-\alpha)^{3 / 2}}\left(0.886+4.64 \alpha-13.32 \alpha^{2}+\right. \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left.14.72 \alpha^{3}-5.6 \alpha^{4}\right) 。\end{array} $ | (1) |
式中:P为外载荷;B为试样厚度;BN=B-2R,其中R为倒角圆弧的半径;
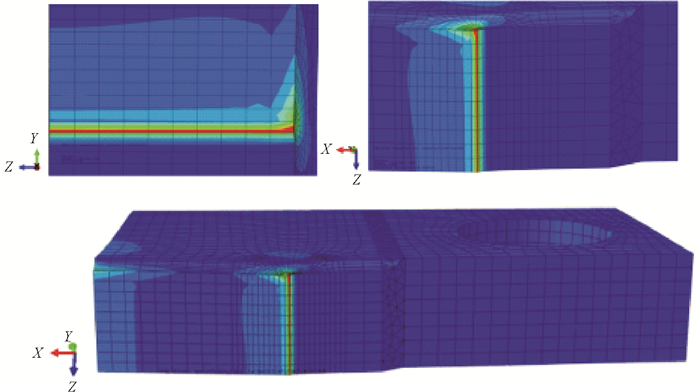
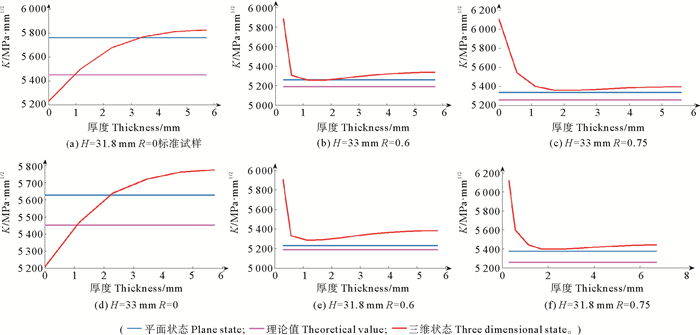
根据ASTM在E647-15e1[18],推荐的CT试样厚度的范围为:W/20≤B≤W/2,对于≥0.2时,式(1)有效。本文试样的选取符合紧凑拉伸试样的范围,与标准CT试样不同之处主要为试样高度H、试样长度L和加载孔径D的取值。本文利用ABAQUS软件模拟得出CT试样一定长度裂纹裂尖处的应力分布,如图 3所示,可直观的看出裂纹扩展前缘应力值最大。同时分别计算出平面状态和三维状态下的应力强度因子并与理论值对比,得出不同尺寸CT试样在平面、三维和理论值的关系,如图 4所示,以及不同尺寸CT试样及标准CT试样的裂纹应力强度因子的计算结果,如表 2所示。
|
图 3 CT试样的应力云图 Fig. 3 Stress cloud pattern of CT specimen |
|
图 4 平面、三维和理论状态下不同尺寸CT试样的应力强度因子 Fig. 4 SIFs under plane, three-dimension and theoretical states of CT specimens of different sizes |
|
|
表 2 不同尺寸CT试样与标准CT试样的应力强度因子值 Table 2 SIF values of CT specimens of different sizes and standard CT specimens |
可以发现,对于标准CT试样而言,采用公式(1)和ABAQUS软件计算得到的名义应力强度因子的最大相对误差很小,仅为3.9%,即软件模拟能够保证应力强度因子的精度,可以基于ABAQUS软件进行CT试样应力强度因子的模拟和计算。对比不同尺寸的CT试样的计算结果可以发现,计算值和理论值误差都处于3.1%以内,二者误差较小,因此可以采用公式(1)计算本试验用CT试样的裂纹应力强度因子值。
2 X65钢腐蚀疲劳试验本试验采用YYF-50高温高压腐蚀疲劳试验机,采用直流电压降法,即DCPD设备测量裂纹长度(见图 5);将CT试样装夹于设备(见图 6);对API X65海底管道用钢开展腐蚀疲劳裂纹扩展试验。

|
图 5 YYF-50腐蚀疲劳试验机 Fig. 5 YYF-50 corrosion fatigue testing machine |

|
图 6 CT试样装夹示意图 Fig. 6 Schematic diagram of side wall grooved CT specimen clamping mode |
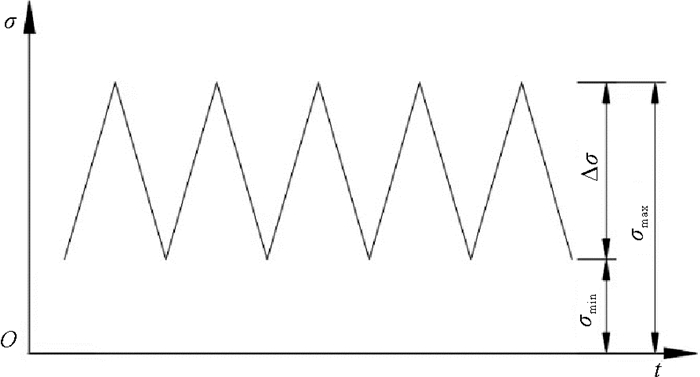
试验前对CT试样进行充分的除油、除锈,以确保在随后的腐蚀疲劳裂纹扩展试验中裂纹尖端无污染,同时采用3.5%NaCl溶液作为腐蚀体系溶液,设定腐蚀疲劳介质的温度为室温,调节腐蚀体系溶液酸碱度使其pH=7,设定加载频率f=1 Hz,应力比R=0.1,采用三角形波进行加载(见图 7)。将CT试样分为三组进行试验,如表 3所示,且每组试样都在恒定应力强度因子K(
|
图 7 腐蚀疲劳试验载荷加载波形 Fig. 7 Load waveform of corrosion fatigue test |
第一组试验在惰性环境空气体系下开展,恒K预制裂纹后采用P=6 000 N的恒幅循环载荷进行裂纹扩展试验,裂纹扩展一定距离后,通过降载的方式使裂纹扩展速度降至10-7 mm·cycle-1时停止试验。第二组试样在3.5%NaCl腐蚀溶液体系中完成,其余加载方式与第一组完全相同。第三组试样同样在3.5%NaCl腐蚀溶液体系中进行,预制裂纹结束后采用P=4 000 N的恒幅循环荷载进行裂纹扩展试验,裂纹扩展速度降至10-7 mm·cycle-1时停止试验。
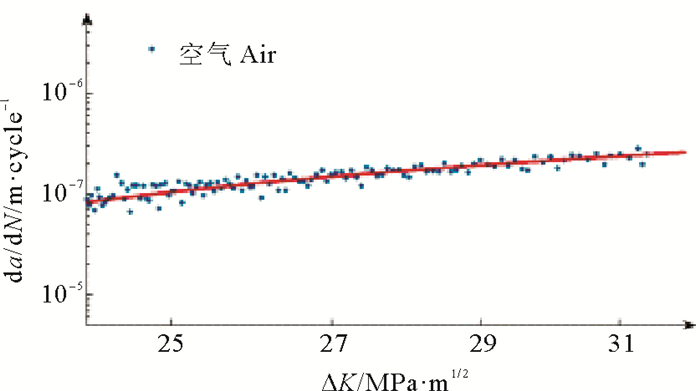
2.2 试验结果分析 2.2.1 空气环境下定载扩展规律分析对第一组试样在双对数坐标系下,建立空气环境下疲劳裂纹扩展速率da/dN与应力强度因子ΔK的关系,如图 8所示。在定幅荷载作用下,空气环境下裂纹扩展的稳定阶段da/dN与ΔK呈线性关系,即可以采用Paris公式进行拟合,拟合结果为:
| $ \frac{\mathrm{d} a}{\mathrm{~d} N}=2.996 \times 10^{-11}(\Delta K)^{2.58} 。$ |
|
图 8 空气环境下试样1的da/dN与ΔK示意图 Fig. 8 da/dN and ΔK of specimen 1 in air system |
定义疲劳裂纹扩展阈值等于10-7 mm·cycle-1所对应的应力强度因子[22],可得到空气体系下的裂纹扩展阈值为
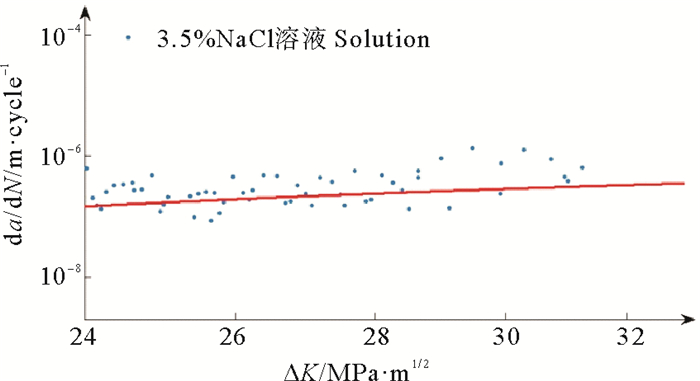
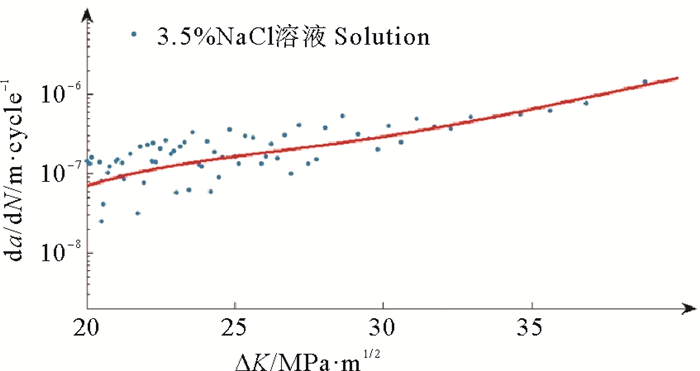
在双对数坐标系下,分别建立腐蚀环境下试验二、三的疲劳裂纹扩展速率da/dN与应力强度因子ΔK的关系,如图 9、10所示。可以看出,在P=6 000 N和P=4 000 N的定幅荷载作用下,腐蚀溶液环境下裂纹扩展的稳定阶段da/dN与ΔK均呈线性关系,同样可以采用Paris公式进行拟合,拟合结果分别为:
| $ \begin{array}{l} \frac{\mathrm{d} a}{\mathrm{~d} N}=5.542 \times 10^{-11}(\Delta K)^{2.58} ;\\ \frac{\mathrm{d} a}{\mathrm{~d} N}=2.265 \times 10^{-11}(\Delta K)^{2.58} 。\end{array} $ |
|
图 9 3.5%NaCl体系下试样2的da/dN与ΔK示意图 Fig. 9 da/dN and ΔK of specimen 2 in 3.5%NaCl system |
|
图 10 3.5%NaCl体系下试样3的da/dN与ΔK示意图 Fig. 10 da/dN and ΔK of specimen 3 in 3.5%NaCl system |
通过对第二组试验数据的进一步分析,得到3.5% NaCl溶液体系下裂纹扩展阈值
对比1、2组试验得到的裂纹扩展门槛值可以发现,3.5%NaCl溶液比空气环境下的裂纹扩展门槛值低3.4 MPa·m
将三组试验的裂纹扩展速率da/dN与应力强度因子幅值ΔK的关系进行对比,如图 11所示。分析可知,腐蚀环境的存在可以提高腐蚀疲劳裂纹的扩展速率,降低裂纹扩展时裂纹面所需要的表面能;同时存在腐蚀环境时,裂纹扩展速率与应力强度因子的关系同样存在线性稳定阶段,此阶段裂纹扩展规律可采用Paris公式拟合。
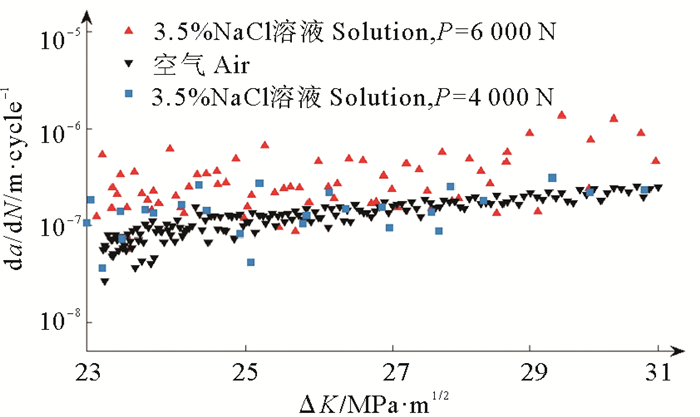
|
图 11 空气和3.5%NaCl体系下da/dN与ΔK示意图 Fig. 11 The relationship between da/dN and ΔK under the system of air and 3.5%NaCl |
试件疲劳裂纹长度与加载周数的关系如表 3所示。可以看出,裂纹同样增长3.9 mm,在3.5%NaCl溶液环境下的试件2比空气环境下的试件1所需加载周数低8 320次;可以证实在1 Hz加载频率下,腐蚀溶液对疲劳裂纹扩展起促进作用。对比腐蚀环境下不同疲劳荷载产生的裂纹长度对应的加载周数,可以发现对于同处于腐蚀环境体系下的试件3比试件2所需加载周数多70 057次,约为试件2加载周数的4倍,即载荷的降低会减缓裂纹扩展速率。
|
|
表 3 CT试件疲劳裂纹长度及加载周数 Table 3 Crack length and cycle times of CT specimens fatigue test |
对比空气和腐蚀环境下断裂后的试样(见图 12(a)、(b))。其中可明显看出,由于裂纹稳定扩展阶段试件裂纹扩展速度较为缓慢,均低于1.510-3 mm·cycle-1,疲劳断口反复张合,断口上下重复挤压摩擦,从而使得在空气和腐蚀环境中的疲劳断口相对光滑。相比于空气环境,在3.5%NaCl溶液环境下的疲劳断口腐蚀较为明显,但并未产生严重的腐蚀痕迹,经分析可能是由于试件与海水在疲劳载荷加载过程中的接触时间较短所导致的。对比腐蚀环境,不同载荷下的疲劳断口(见图 12(b)、(c))。可以发现,相比于第2组试样,第3组试样在稳定扩展阶段由于施加载荷较低,腐蚀疲劳断口循环摩擦次数较高,因此断口更为平滑;同时由于加载周数的增多,试样与腐蚀溶液接触时间增长,腐蚀效果相对明显。

|
图 12 三组CT试样断口 Fig. 12 Three groups of CT specimen fractures |
利用ABAQUS软件,对CT试样的裂纹应力强度因子展开分析;制备X65钢材质的CT试样,开展腐蚀疲劳裂纹扩展试验,可得到以下结论:
(1) 对于侧壁开槽且存在一定尺寸差异的CT试样,可以采用ASTM标准推荐的应力强度因子表达式对不同尺寸下的裂纹应力强度因子进行计算。
(2) 增长相同的裂纹长度,在3.5%NaCl溶液环境下比空气环境下所需加载周数低8 320次;同时3.5%NaCl溶液环境比空气体系下的裂纹扩展阈值低25%。因此和惰性环境(空气)相比,腐蚀环境的存在可明显的加快腐蚀疲劳裂纹的扩展速率以及降低裂纹扩展的阈值。
(3) 存在腐蚀环境时,裂纹扩展速率与应力强度因子的关系同样存在线性稳定阶段,此阶段裂纹扩展规律可采用Paris公式拟合。
| [1] |
余建星. 深海油气工程[M]. 天津: 天津大学出版社, 2010. Yu J X. Deep Sea Oil and Gas Engineering[M]. Tianjin: Tianjin University Press, 2010. (  0) 0) |
| [2] |
Yang Y S, Khan F, Thodi P, et al. Corrosion induced failure analysis of subsea pipelines[J]. Reliability Engineering and System Safety, 2017, 159: 214-222. DOI:10.1016/j.ress.2016.11.014
(  0) 0) |
| [3] |
Bhandari J, Khan F, Abbassi R, et al. Modelling of pitting corrosion in marine and offshore steel structures-A technical review[J]. Journal of Loss Prevention in the Process Industries, 2015, 37: 39-62. DOI:10.1016/j.jlp.2015.06.008
(  0) 0) |
| [4] |
Larrosa N O, Akid R, Ainsworth R A. Corrosion fatigue: A review of damage tolerance model[J]. International Materials Reviews, 2018, 63(5): 283-308. DOI:10.1080/09506608.2017.1375644
(  0) 0) |
| [5] |
DNV. Fatigue Assessment of Ship Structures[M]. Veritasveien, Hovik: Det Norske Veritas, 2010.
(  0) 0) |
| [6] |
ABS. Guide for the Fatigue Assessment of Offshore Structures-Section 3 S-N curves[M]. Houston: American Bureau of Shipping, 2003.
(  0) 0) |
| [7] |
Kang D H, Lee J K, Kim T W. Corrosion fatigue crack propagation of high-strength steel HSB800 in a seawater environment[J]. Procedia Engineering, 2011(10): 1170-1175.
(  0) 0) |
| [8] |
Cheng A K, Chen N Z. An extended engineering critical assessment for corrosion fatigue of subsea pipeline steels[J]. Engineering Failure Analysis, 2018, 84: 262-275. DOI:10.1016/j.engfailanal.2017.11.012
(  0) 0) |
| [9] |
杨斌, 陈吉, 耿越, 等. 2205双相不锈钢在水溶液中的疲劳裂纹扩展行为[J]. 腐蚀科学与防护技术, 2018, 30(2): 182-186. Yang B, Chen J, Geng Y, et al. Corrosion fatigue crack progation behavior of 2205 duplex stainless steel in aqueous medium[J]. Corrosion Science and Protection Technology, 2018, 30(2): 182-186. (  0) 0) |
| [10] |
Zhao T L, Liu Z Y, Du C W, et al. Corrosion fatigue crack initiation and initial propagation mechanism of E690 steel in simulated seawater[J]. Materials Science and Engineering, 2017, 708: 181-192. DOI:10.1016/j.msea.2017.09.078
(  0) 0) |
| [11] |
Zhao T L, Liu Z Y, Du C W, et al. Modeling for corrosion fatigue crack initiation life based on corrosion kinetics and equivalent initial flaw size theory[J]. Corrosion Science, 2018, 142: 277-283. DOI:10.1016/j.corsci.2018.07.031
(  0) 0) |
| [12] |
Kovalov D, Fekete B, Engelhardt G R, et al. Prediction of corrosion fatigue crack growth rate in alloys, Part Ⅰ: General corrosion fatigue model for aero-space aluminum alloys[J]. Corrosion Science, 2018, 141: 22-29. DOI:10.1016/j.corsci.2018.06.034
(  0) 0) |
| [13] |
Gao P F, Lei Z N, Wang X X, et al. Deformation in fatigue crack tip plastic zone and its role in crack propagation of titanium alloy with tri-modal microstructure[J]. Materials Science and Engineering, 2019, 739: 198-202. DOI:10.1016/j.msea.2018.10.049
(  0) 0) |
| [14] |
Qi S, Cai L X, Bao C, et al. The prediction models for fatigue crack propagation rates of mixed-mode Ⅰ-Ⅱ cracks[J]. Engineering Fracture Mechanics, 2019, 205: 218-228. DOI:10.1016/j.engfracmech.2018.11.018
(  0) 0) |
| [15] |
Andrade H C, Leonel E D. The multiple fatigue crack propagating on modelling in nonhomogeneous structures using the DBEM[J]. Engineering Analysis with Boundary Elements, 2019, 98: 296-309. DOI:10.1016/j.enganabound.2018.10.026
(  0) 0) |
| [16] |
Sun J Z, Ding Z H, Huang Q. Corrosion fatigue life prediction for steel bar in concrete based on fatigue crack propagation and equivalent initial flaw size[J]. Construction and Building Materials, 2019, 195: 208-217. DOI:10.1016/j.conbuildmat.2018.11.056
(  0) 0) |
| [17] |
Brooking L, Gray S, Sumner J, et al. Effect of stress state and simultaneous hot corrosion on the crack propagation and fatigue life of single crystal superalloy CMSX-4[J]. International Journal of Fatigue, 2018, 116: 106-117. DOI:10.1016/j.ijfatigue.2018.05.002
(  0) 0) |
| [18] |
ASTM. ASTM E647-15 Standard Test Method for Measurement of Fatigue Crack Growth Rates[S]. West Conshohocken, PA: American Society for Testing Material, 2016.
(  0) 0) |
| [19] |
Iman Ameli, Behrouz Asgarian, Meng Lin, et al. Estimation of the CTOD-crack growth curves in SENT specimens using the eXtended finite element method[J]. International Journal of Pressure Vessels and Piping, 2019, 169: 16-25. DOI:10.1016/j.ijpvp.2018.11.008
(  0) 0) |
| [20] |
British Standards Institute. BS 8571: 2014 Method of Test for Determination of Fracture Toughness in Metallic Materials Using Single Edge Notch Tension (SENT) Specimen[S]. Lundon: BSI Standards Limited, 2014.
(  0) 0) |
| [21] |
Goswami T K, Hoeppner D W. Pitting corrosion fatigue of structural materials[M]. // Chang C I, Sun C T. Structural Integrity in Aging Aircraft, AD-vol. 47. New York: ASME, 1995.
(  0) 0) |
| [22] |
北京航空材料研究院. GB_T 6398-2000金属材料疲劳裂纹扩展速率试验方法[S]. 北京: 中国标准出版社, 2000. AECC Beijing Institute of Aeronautical Materials. GB_T 6398-2000 Test Method for Fatigue Crack Propagation Rate of Metallic Materials[S]. Beijing: Standards Press of China, 2000. (  0) 0) |
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
 2021, Vol. 56
2021, Vol. 56


