海洋湍流剪切数据是进行海洋微结构湍流研究的重要原始资料,对建立海洋物理模型进而研究海洋宏观运动有重要意义[1]。通过剪切数据计算得到的湍流动能耗散率,是湍流的一个重要特征参数。
Osborn团队于1970年代首先研制出搭载翼型剪切流传感器的垂直微结构湍流剖面仪,并成功进行测量海洋微结构湍流[2]。垂直微结构湍流剖面仪(以下简称湍流仪)是目前获取海水剪切流数据最普遍和最有效的平台之一,已受到海洋领域科研人员的普遍认可。
加拿大Rockland公司研制的VMP系列和德国ISW Wasser公司与SST公司合作研发MSS系列湍流仪是当前最具代表性的,得到国际市场的广泛认可。在国内,天津大学率先开展对湍流仪的研制,目前已研制成功第三代样机。本文以实验室自主研发的下放式湍流仪为研究对象,对其相关性能进行分析。
湍流仪下潜过程中,剪切传感器通过探针以一定的频率测量微结构湍流水平方向的脉动信号。根据下潜速度和攻角,计算微结构湍流脉动在时域、频域和空间波数域的强度,进而计算湍流动能耗散率[3]。湍流脉动频率和下潜速度成正比,而剪切传感器的固有频率决定脉动频率的测量上限[4]。剪切信号在频域和波数域上的分析皆基于湍流的脉动频率。
姿态会影响水流攻角,在小范围内,剪切传感器输出信号幅值与水流攻角近似成正比[5]。过大的倾角会导致测量误差加剧,给数据分析带来困难。
仪器的固有频率决定流致振动的频率[6],而流致振动频率决定湍流耗散率的测量下限[7]。同时,流致振动会带来严重的噪音信号,影响剪切传感器的工作性能。
因此,合理而稳定的下潜速度、良好的下潜姿态以及小固有频率,对于准确可靠的测量湍流动能耗散率具有十分关键的作用。通过动力学分析,研究结构对这些因素间影响,能够为后期数据处理及结构优化提供帮助。
1 运动模型建立 1.1 运动坐标系湍流仪在下潜的时候,由于受到流场的的影响,受力不平衡,会出现绕轴摆动。此时,其速度可以分解为两部分:旋转中心的直线速度,以及绕轴转动。
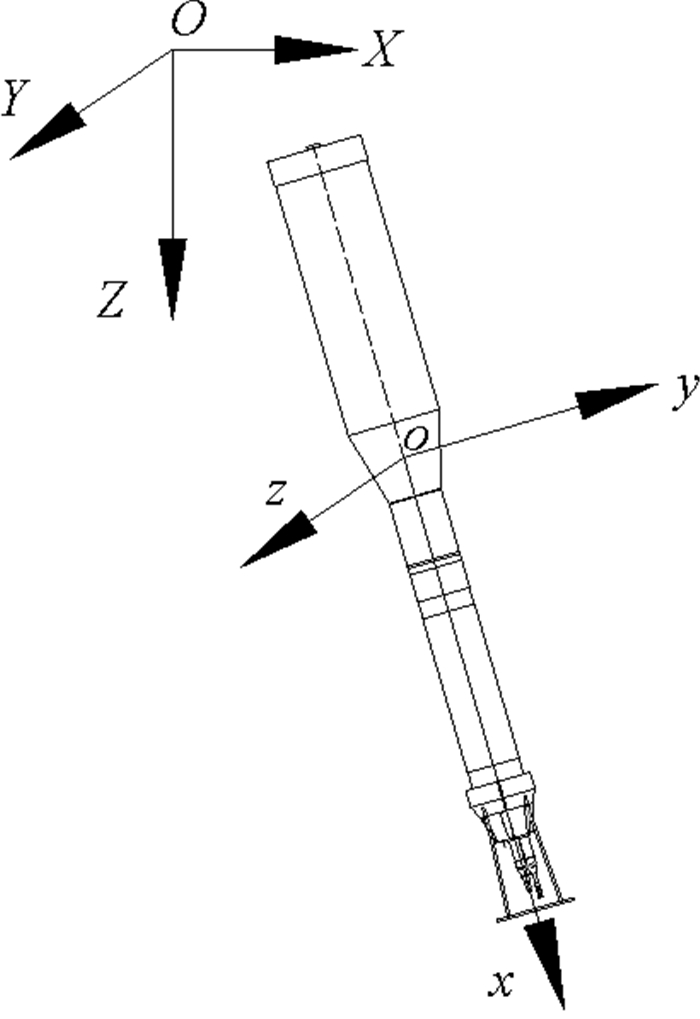
为便于分析,参考水下滑翔机的运动模型建立方法[8],采用双坐标系对湍流仪的运动进行分析,坐标系如图 1所示。
|
图 1 运动坐标系 Fig. 1 Motion coordinate systems |
图 1中,OXYZ是绝对坐标系,O为仪器入水点,XOY为海平面,Z为竖直向下方向。oxyz为相对坐标,以仪器自身为参考,o为仪器自由转动的中心点,x为轴线方向,xoy为XOZ的平行面。
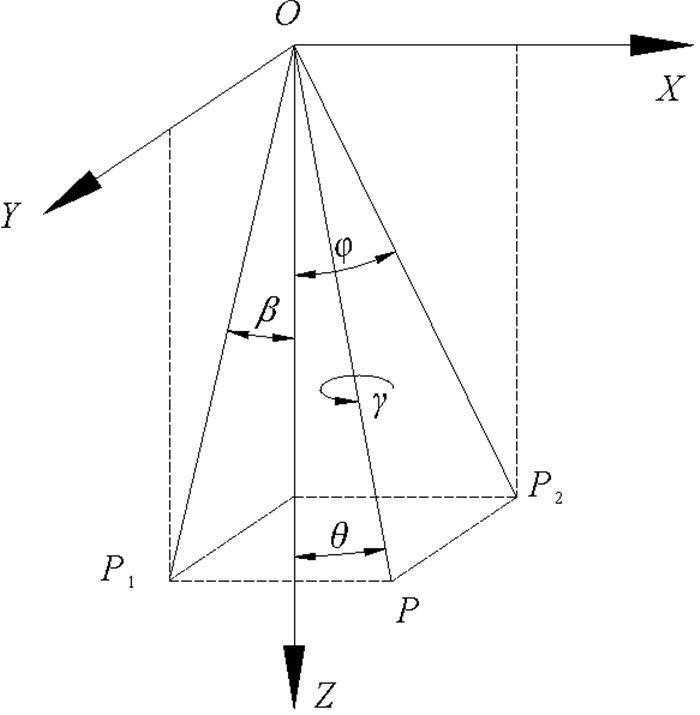
湍流仪内置姿态传感器,用偏航角、俯仰角和翻滚角(Heading-Pitch-Roll)三个角参数来描述仪器姿态。在OXYZ坐标系下,描述仪器的三个姿态角,坐标系如图 2所示。
|
图 2 姿态角参考坐标系 Fig. 2 Coordinate system for attitude angles |
在图 2中,OP为湍流仪轴线的平行线,OP1和OP2分别为OP在YOZ′和XOZ平面上的投影。β、φ、γ分别对应偏航角、俯仰角和翻滚角[9]。由于MTI姿态传感器安装时固定面的不同,三个姿态角数据可能存在互换。
角θ为仪器的倾角,即与竖直方向的夹角。仪器在平面内摆动时,β、φ符号要么保持相同,要么不同,变化率也成线性关系。因此,定义θ与β同正负,其值可以通过角β、φ计算得到:
| $ \theta = \arctan \left( {\sqrt {{{\tan }^2}\beta + {{\tan }^2}\varphi } } \right)。$ | (1) |
在倾斜较小的情况下,上式通过近似简化为:
| $ \theta = \sqrt {{\beta ^2} + {\varphi ^2}} 。$ | (1*) |
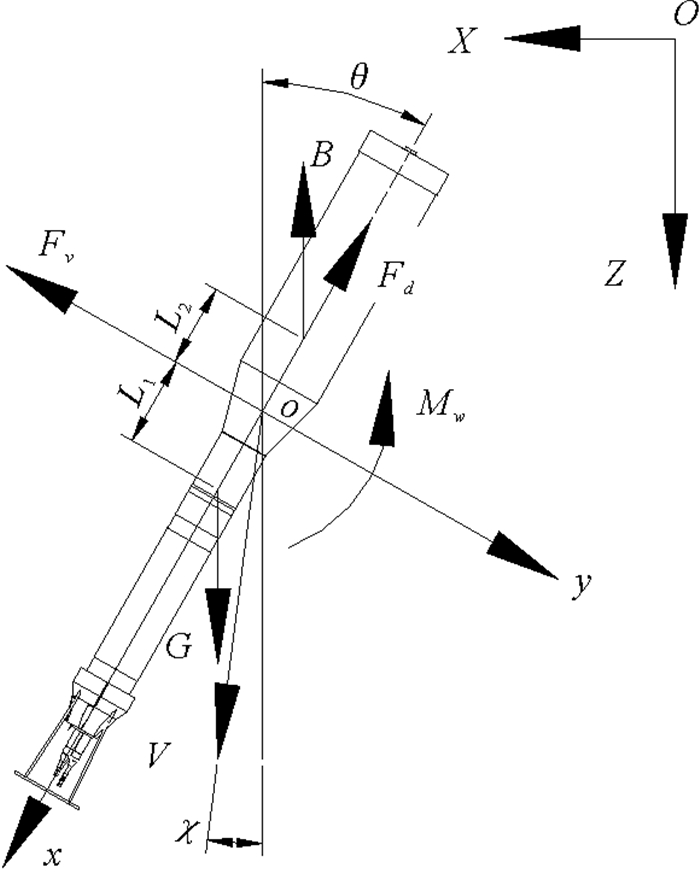
在局部海域,海流方向具有一致性,即V在一个确定的平面内,假设其在Y轴(z轴)上的速度分量为0。为简化分析,将湍流仪在空间的运动降到二维坐标进行分析,其运动模型如图 3。
|
图 3 动力学模型图示 Fig. 3 Graphical kinetic model |
在图 3中,V为湍流仪o点相对周围流体平均流动的相对运动速度,m/s;χ为V与Z轴夹角,rad。G和B分别为重力和浮力,N;L1和L2分别为重心和浮心到旋转中心的距离,m。Fv为流体对仪器y轴方向的冲击力合力,N;Fd为流体对仪器x轴方向的阻力合力,N;Mw为流体作用力对o点的合力矩,N·m。不考虑湍流脉动,水流平均速度对剪切传感器的攻角α=θ-χ。
在二维坐标系下,湍流仪模型有三个自由度,即三个变量:X、Z和θ。此模型下,湍流仪的速度可分解为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{V}}_X} = \mathit{\boldsymbol{V}}\sin \chi }\\ {{\mathit{\boldsymbol{V}}_Z} = \mathit{\boldsymbol{V}}\cos \chi } \end{array}} \right.; $ | (2) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{V}}_x} = \mathit{\boldsymbol{V}}\cos (\theta - \chi ) = {\mathit{\boldsymbol{V}}_X}\sin \theta + {\mathit{\boldsymbol{V}}_Z}\cos \theta }\\ {{\mathit{\boldsymbol{V}}_y} = \mathit{\boldsymbol{V}}\sin (\theta - \chi ) = - {\mathit{\boldsymbol{V}}_X}\cos \theta + {\mathit{\boldsymbol{V}}_Z}\sin \theta } \end{array}} \right.。$ | (3) |
引入速度分量矩阵
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{V}}_{XZ}} = [\mathit{\boldsymbol{\chi }}]\mathit{\boldsymbol{V}}}\\ {{\mathit{\boldsymbol{V}}_{xy}} = [\mathit{\boldsymbol{\theta }}]{\mathit{\boldsymbol{V}}_{XZ}} = [\mathit{\boldsymbol{\theta }}][\mathit{\boldsymbol{\chi }}]\mathit{\boldsymbol{V}}} \end{array}} \right.。$ | (4) |
基于上述模型,在两个坐标系下分别建立动力学微分方程组:
| $ \left\{ {\begin{array}{*{20}{l}} {m\frac{{\partial {\mathit{\boldsymbol{V}}_x}}}{{\partial t}} = \left( {\mathit{\boldsymbol{G}} - \mathit{\boldsymbol{B}}} \right)\cos \theta - {\mathit{\boldsymbol{F}}_D}\;\;\;\;\;\;\;\;\;\;\;\;({\rm{a}})}\\ {m\frac{{\partial {\mathit{\boldsymbol{V}}_y}}}{{\partial t}} = \left( {\mathit{\boldsymbol{G}} - \mathit{\boldsymbol{B}}} \right)\sin \theta - {\mathit{\boldsymbol{F}}_v}\;\;\;\;\;\;\;\;\;\;\;\;\;({\rm{b}})}\\ {J\frac{{{\partial ^2}\theta }}{{\partial {t^2}}} = - \left( {\mathit{\boldsymbol{G}}{L_1} + \mathit{\boldsymbol{B}}{L_2}} \right)\sin \theta - {\mathit{\boldsymbol{M}}_w}\;\;\;\;({\rm{c}})} \end{array}} \right.。$ | (5) |
| $ \left\{ {\begin{array}{*{20}{l}} {m\frac{{\partial {\mathit{\boldsymbol{V}}_X}}}{{\partial t}} = {\mathit{\boldsymbol{F}}_v}\cos \theta - {\mathit{\boldsymbol{F}}_d}\sin \theta \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\rm{a}} \right)}\\ {m\frac{{\partial {\mathit{\boldsymbol{V}}_Z}}}{{\partial t}} = \left( {\mathit{\boldsymbol{G}} - \mathit{\boldsymbol{B}}} \right) - \left( {{\mathit{\boldsymbol{F}}_v}\sin \theta + {\mathit{\boldsymbol{F}}_d}\cos \theta } \right)\;\;\;\;\;\left( {\rm{b}} \right)}\\ {J\frac{{{\partial ^2}\theta }}{{\partial {t^2}}} = - \left( {\mathit{\boldsymbol{G}}{L_1} + \mathit{\boldsymbol{B}}{L_2}} \right)\sin \theta - {\mathit{\boldsymbol{M}}_w}\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\rm{c}} \right)} \end{array}} \right.。$ | (5*) |
式中:m为总质量,kg;J为等效转动惯量,kg·m2。
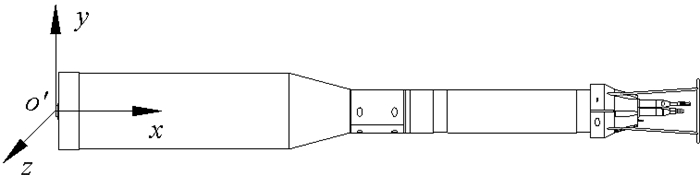
2 参数计算湍流仪总长为1 800 mm,耐压舱长度810 mm,外径125 mm,浮体长780 mm,外径D=220 mm。以仪器最尾端为参考平面,其与仪器轴线的交点为坐标原点,建立坐标系,用于其他重要结构参数分析,其坐标系见图 4。
|
图 4 重浮力配置坐标系 Fig. 4 Coordinate system for configuration of gravity and buoyancy |
在此参考系下,相关结构参数汇总见表 1。
|
|
表 1 结构动力学参数 Table 1 Kinetic parameters of the structure |
根据能量最低原理,湍流仪受到外力作用时,会绕转动惯量最小的轴旋转[10]。由于转动时有附加质量(排开水的质量)存在,转动中心o不在质心处,而是位于重浮心之间,到重心的距离为:
| $ {L_1} = \frac{m}{{m + {m_w}}}L。$ | (6) |
式中:m为湍流仪质量,mw为排水质量,L为重浮心距离。通过计算,得到L1=0.092 m,转动中心o位于距尾端0.722 m处。
仪器对旋转中心o的转动惯量为:
| $ J = {J_1} + mL_1^2 + {J_2} + {m_w}L_2^2。$ | (7) |
式中:J1为仪器转动惯量,J2为附加质量(即排开的水)转动惯量。将相关参数代入,可得J=16.57 kg·m2。
2.2 流体作用力在动力学模型中,湍流仪上有三个与流场相关的作用力:阻力Fd、冲击力Fv以及冲击力矩Mw。
Fd力方向与Vx相反,其中阻力系数CD已经通过计算得到。阻尼刷丝长为200 mm,CD=2.945,计算公式如下:
| $ {\mathit{\boldsymbol{F}}_d} = \frac{1}{2}\rho {C_D}A\mathit{\boldsymbol{V}}_x^2 = 53.04\mathit{\boldsymbol{V}}_x^2。$ | (8) |
式中:ρ为流体密度,kg/m3;A为迎流面积,m2。采用标准单位进行计算后,登时左右为仅数值相等关系,下同。Fv为流场在y轴方向相对流速对仪器的冲击力,其方向与Vy相反。在很大范围内,流体对圆柱体的阻力系数为CD*=1[11]。考虑仪器转动的影响,Fv的值为:
| $ {\mathit{\boldsymbol{F}}_v} = \frac{1}{2}\rho C_D^*515\int_{{L^\prime } - L}^{{L^\prime }} D (l)\left( {{\mathit{\boldsymbol{V}}_y} + l\frac{{\partial \theta }}{{\partial t}}} \right)\left| {{\mathit{\boldsymbol{V}}_y} + l\frac{{\partial \theta }}{{\partial t}}} \right|{\rm{d}}l。$ | (9) |
式中:L′为最尾端到o点的距离,L为总长,D(l)为该处直径,m。若仪器不存在转动,仪器受到的冲击力合力为:
| $ {\mathit{\boldsymbol{F}}_v} = \frac{1}{2}\rho C_D^*\mathit{\boldsymbol{V}}_y^2\int_{L' - L}^{L'} {D\left( l \right){\rm{d}}l} = 151.49\mathit{\boldsymbol{V}}_y^2。$ | (10) |
Fd作用于仪器一周,对o取矩为0,因此合力矩Mw只与Fv有关。在分析转动惯量时,已将附加质量考虑在内,此处只计算由Fv引起的力矩,其公式为:
| $ {\mathit{\boldsymbol{M}}_w} = \frac{{\rho C_D^*}}{2}\int_{L'' - L}^{L''} {\left| {lD(l){{\left( {{\mathit{\boldsymbol{V}}_y} + l\frac{{\partial \theta }}{{\partial t}}} \right)}^2}} \right|{\rm{d}}l} + \left( {L' - L''} \right){\mathit{\boldsymbol{F}}_v}。$ | (11) |
式中,L″为最尾端到Vy=0点的距离,m。若仪器不存在转动,那么:
| $ {\mathit{\boldsymbol{M}}_w} = 2.84\mathit{\boldsymbol{V}}_y^2。$ | (12) |
分析下潜速度不考虑仪器的倾斜,即仪器只有Z轴方向的速度。根据公式(5*(b)),结合坐标转换公式,可以得出关于下潜速度VZ的关系式:
| $ \frac{1}{2}\rho {C_D}A\mathit{\boldsymbol{V}}_Z^2 = \left( {\mathit{\boldsymbol{G}} - \mathit{\boldsymbol{B}}} \right) - m\frac{{\partial {\mathit{\boldsymbol{V}}_Z}}}{{\partial t}}。$ | (13) |
上式是带二次项的微分方程,难以析解。但是,在足够长时间后,重力、浮力和水阻力达到平衡,加速度为0,速度趋于稳定,那么公式13可化为:
| $ {\left. {{\mathit{\boldsymbol{V}}_Z}} \right|_{t = \infty }} = \sqrt {\frac{{2\left( {\mathit{\boldsymbol{G}} - \mathit{\boldsymbol{B}}} \right)}}{{{C_D}\rho A}}}。$ | (14) |
加入配重结构,可以改变仪器下潜速度,配重使用铅块密度为11.3 g/cm3,每100 g铅块在海水中净重为91 g。加入配重质量N kg,净重(0.06+0.91N)kg。结合阻力Fd,此时仪器的稳定速度:
| $ {\left. {{\mathit{\boldsymbol{V}}_Z}} \right|_{t = \infty }} = \sqrt {\frac{{\left( {0.06 - 0.91N} \right)g}}{{53.04}}} 。$ | (14*) |
式中,g为重力加速度,取9.81 m/s2。
4 稳定姿态当仪器处于动态稳定,线加速度和角加速度均为0,即要满足∂Vx/∂t=0,∂Vy/∂t=0,∂2θ/∂t2=0,公式(5)代入参数后得:
| $ \left\{ {\begin{array}{*{20}{l}} {0.59\cos \theta = 53.04\mathit{\boldsymbol{V}}_x^2}\\ {0.59\sin \theta = 75.82\mathit{\boldsymbol{V}}_y^2}\\ {71.53\sin \theta = - 2.84\mathit{\boldsymbol{V}}_y^2} \end{array}} \right.。$ | (15) |
此方程组的唯一解是:θ=0,Vy=0,Vx=0.105。转换为XOZ坐标系下的速度:
| $ {\mathit{\boldsymbol{V}}_{XZ}} = {\left[ \mathit{\boldsymbol{\theta }} \right]^{ - 1}}{\mathit{\boldsymbol{V}}_{xy}} = \left[ {\begin{array}{*{20}{c}} 0\\ {0.105} \end{array}} \right]。$ |
此即公式(14*)中,M=0时的下潜速度配置。此时,Z轴方向的速度,χ=0,α=0。换而言之,只要倾角不为0,仪器就不可能处于动态平衡,必然存在某一参数的加速度。
仅考虑姿态的平衡,∂2θ/∂t2=0,分析VX和VZ对θ的影响。将浮力用重力近似替代,根据公式(5(c)),代入力矩参数后:
| $ \mathit{\boldsymbol{G}}L\sin \theta + 2.84{\left( {{\mathit{\boldsymbol{V}}_Z}\sin \theta } \right)^2} = 2.84{\left( {{\mathit{\boldsymbol{V}}_X}\cos \theta } \right)^2}; $ | (16) |
| $ \mathit{\boldsymbol{V}}_X^2 = \frac{{\mathit{\boldsymbol{G}}L}}{{2.84}}\frac{{\tan \theta }}{{\cos \theta }} + {\left( {\tan \theta {\mathit{\boldsymbol{V}}_Z}} \right)^2}。$ | (16*) |
从上式可以得出,在VX和VZ确定的情况下,重浮心距离L越大,角θ越小。假定VZ=0,对θ和VX关系进行定性分析得:
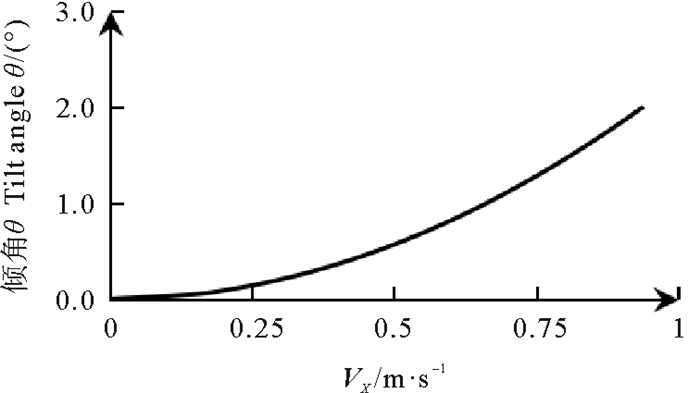
| $ \mathit{\boldsymbol{V}}_X^2 = 25.19\frac{{\tan \theta }}{{\cos \theta }}。$ | (17) |
其函数曲线见图 5。
|
图 5 VX对倾角的影响 Fig. 5 Effect to tilt angle from VX |
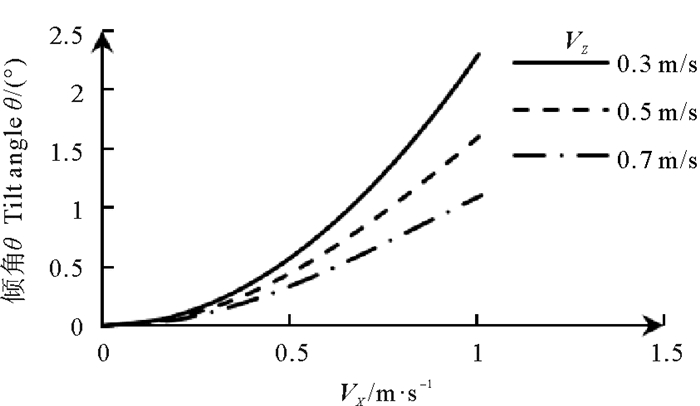
随着VX变大,θ几乎成二次型增大,VX对仪器稳定性影响十分明显。分析不同VZ下θ和VX和关系,具体结果见图 6。
|
图 6 不同VZ对倾角的影响 Fig. 6 Effect to tilt angle from variational VZ |
从结果可以看出,相同VX下,VZ越大,出现的倾角越小。因此,较大的下潜速度有助于仪器姿态的稳定。
倾角与攻角的差值χ只与VX和VZ有关:
| $ \chi = \arctan \frac{{{\mathit{\boldsymbol{V}}_X}}}{{{\mathit{\boldsymbol{V}}_Z}}}。$ | (18) |
相同VX下,VZ越大,χ越小,即姿态数据越接近于攻角。
综上可以得出,L和VZ越大,仪器稳定性越好,攻角也越小。
5 自由摆动分析湍流仪下潜过程中的自由摆动,即θ的变化规律,假定V=0。从Mw可以看出,公式(5(c))是一个非线性振动模型的微分方程,Mw为与多个参数相关的非线性阻尼。若不考虑流场的作用力,只分析重力和浮力的作用。即不考虑阻尼的影响,取Mw=0。考虑在小范围摆动时(θ < 5°),sinθ近似于θ。那么可以将方程简化为线性无阻尼自由振动模型:
| $ J\frac{{{\partial ^2}\theta }}{{\partial {t^2}}} + \left( {\mathit{\boldsymbol{G}}{L_1} + \mathit{\boldsymbol{B}}{L_2}} \right)\theta = 0。$ | (19) |
这是典型的简谐振动模型,结构固有频率为:
| $ {\omega _n} = \sqrt {\frac{{\mathit{\boldsymbol{G}}{L_1} + \mathit{\boldsymbol{B}}{L_2}}}{{{J_1} + mL_1^2 + {J_2} + {m_w}L_2^2}}} 。$ | (20) |
对于本结构,由于mw与m十分接近,用m代如计算。基于J1和J2不随L发生变化假定,上式可写为:
| $ {\omega _n} = \sqrt {\frac{{mgL}}{{{J_1} + {J_2} + m{L^2}/2}}} 。$ | (20*) |
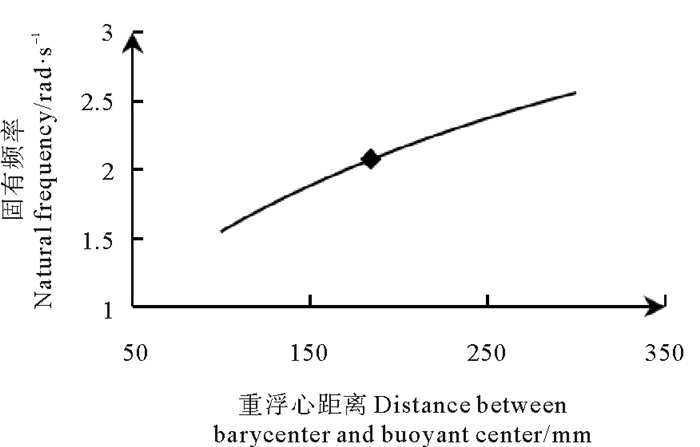
其关系如7图所示。
|
图 7 结构固有频率 Fig. 7 Natural frequency of structure in different configuration |
从图 7中可以看出,随着重浮心距离变大,固有频率也随之变大。将具体参数代入到公式中,可以得出:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _n} = \sqrt {\frac{{71.53}}{{16.57}}} = 2.078\;{\rm{rad}}/{\rm{s}}}\\ {{f_n} = \frac{{{\omega _n}}}{{2{\rm{ \mathsf{ π} }}}} = 0.331\;{\rm{Hz}}} \end{array}} \right.。$ | (21) |
在固有频率下,湍流仪倾角及角速度的时间函数为:
| $ \left\{ {\begin{array}{*{20}{l}} {\theta = {\theta _m}\sin (2.078t + \tau )}\\ {\omega = \frac{{\partial \theta }}{{\partial t}} = 2.078{\theta _m}\cos (2.078t + \tau )} \end{array}} \right.。$ | (22) |
上式中,θm为摆动幅值,τ为初始相位。对应剪切传感器探针处因自由摆动带来y轴方向速度为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_t} = \omega l = 2.172{\theta _m}\cos (2.078t + \tau )}\\ {{\mathit{\boldsymbol{a}}_t} = \frac{{\partial {v_t}}}{{\partial t}} = - 4.513{\theta _m}\sin (2.078t + \tau )} \end{array}} \right.。$ | (23) |
在此摆动频率下,max(|at|) = 4.513θm,单位为m/s2。
无阻尼振动振幅不会衰减,实际中不存在。考虑阻尼的存在,根据公式11得:
| $ {\mathit{\boldsymbol{M}}_w} = 21.58\left( {\frac{{\partial \theta }}{{\partial t}}} \right)\left| {\frac{{\partial \theta }}{{\partial t}}} \right|。$ | (24) |
因此完整的摆动模型为:
| $ \frac{{{\partial ^2}\theta }}{{\partial {t^2}}} + 1.30\left( {\frac{{\partial \theta }}{{\partial t}}} \right)\left| {\frac{{\partial \theta }}{{\partial t}}} \right| + 4.32\theta = 0。$ | (25) |
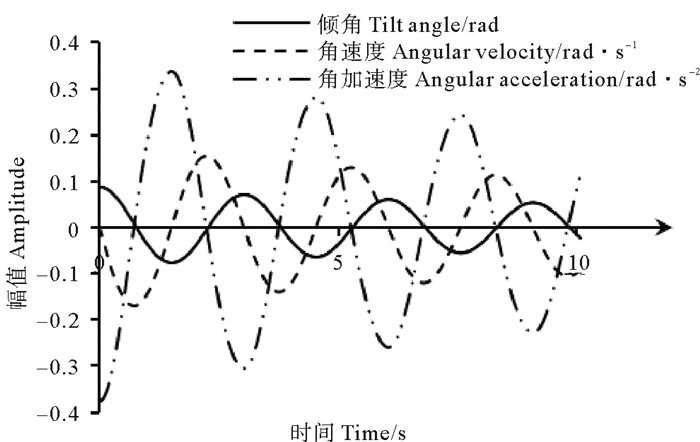
阻尼力大小与角速度平方成正比,是一个二次非线性阻尼。二次阻尼不会改变系统的固有频率,幅值衰减一段时间后系统开始做简谐振动[12]。通过数值算法来求近似解,定性分析振动衰减特性。定义t0时刻θ=0.087 rad(5°),角速度为0。计算角度、角速度、角加速度随时间变化分别如图 8所示:
|
图 8 振动方程数值结算结果 Fig. 8 Numerical results of the vibration equation |
图 8给出了各个参数随时间的变化,可以看出,随着时间的推移,振动周期几乎不变,而振动幅值在阻尼力的作用下持续衰减。为了更明确的分析衰减特性,计算后统计前8个角度峰值出现的时间和幅值(见表 2)。
|
|
表 2 θ峰值数据 Table 2 Data on peaks of tilt angle |
衰减幅度η为与上一个幅值的比值。从表 2中数据分析,系统的摆动周期为3.02 s,振动频率为0.331 Hz,即上面计算结构的固有频率。随着时间推移,幅值变动幅度越来越小,相应的阻尼系数也越来越小,直到振幅平稳。因此,在信号处理时,必须注意该频率振动的影响。
6 试验数据分析 6.1 配速试验在湍流仪完成后,在青岛市南姜码头先后进行了多次配速试验。试验水深约20 m,相同配置进行多次试验,取平均值用于比较。摘取部分试验速度数据如表 3所示。
|
|
表 3 下潜速度试验数据摘录 Table 3 Extract of test data on sinking velocity |
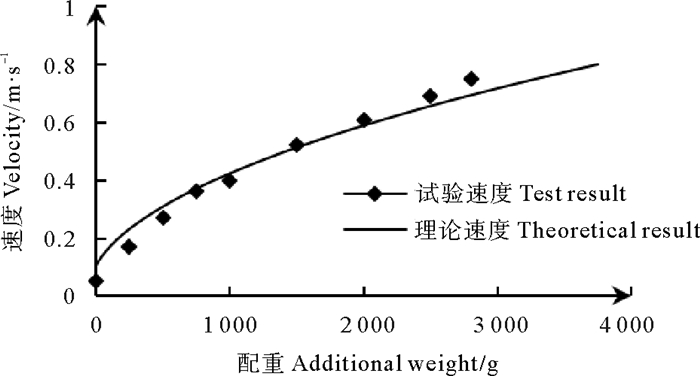
将试验速度与理论速度进行比较,结果见图 9。
|
图 9 理论与试验结果比较 Fig. 9 Comparison of theoretical and experimental results |
从图 9中可以看出,在小于配置速度(< 0.3 m/s)部分,试验速度明显低于理论速度,分析为仪器受缆绳拖曳影响较大所致。在配置速度范围(0.3~0.7 m/s)内,理论计算的速度误差较小,十分接近试验结果。之后,随着配置增大,试验速度变化率明显大于理论速度,可能是因为阻尼刷丝变形导致阻力系数变小。由于在码头试验受到风浪、堤坝和试验母船的影响,通过传感器数据计算以及试验时测得平均速度与实际速度间均可能存在较大误差。
6.2 姿态分析2016年7月,湍流仪跟随东方红2号科考船在南海进行了第二次海试。海试中,将无包塑的细缆系于湍流仪尾部进行布放。将湍流仪下放至海面下后等待一段时间,待其稳定后松开缆绳同时让缆绳始终保持松弛状态。当仪器到达设定深度后,通过拖拽缆绳回收。此次海试共完成三个剖面的测量,成三个剖面的测量,相关信息记录如见表 4。
|
|
表 4 南海海试记录 Table 4 Record of test in the South China Sea |
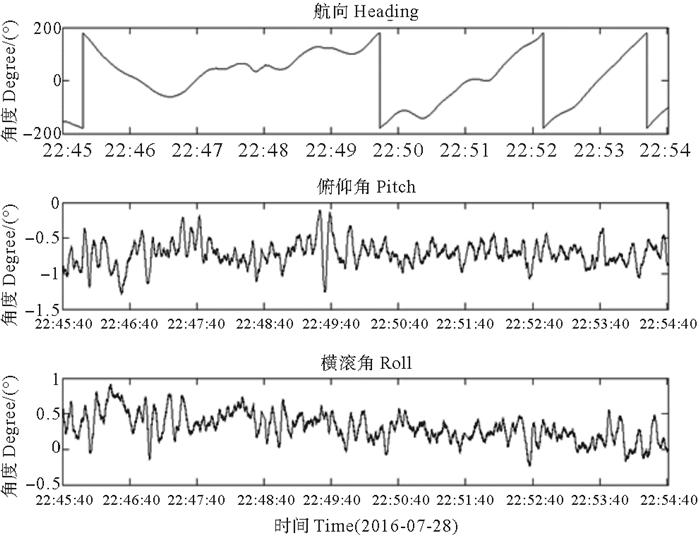
由于安装方式不同,姿态传感器的Heading、Pitch、Roll三个姿态角对应会有变化。下面数据中,Heading为湍流仪自身转动角度,Pitch和Roll为与竖直方向的夹角,下潜过程姿态变化时域信号如图 10所示。
|
图 10 姿态角时域信号 Fig. 10 Time-domain signal of attitude angles |
由于湍流仪实际重浮心偏离轴线、加工和安装误差及受水阻力不平衡等原因,Pitch和Roll角的平衡位置并不在0°。从图 10分析,Pitch角平均值为-0.7°,Roll角平均值为0.3°。假设姿态传感器安装面与仪器轴线完全垂直,根据公式2,湍流仪平均倾角为:
| $ \theta = \sqrt {{\beta ^2} + {\varphi ^2}} = {0.76^\circ } = 0.013{\rm{rad}}。$ |
湍流仪倾斜较小,且姿态稳定,未出现较大的姿态角。姿态没有出现持续偏离平均值,受到横向水流的影响较小,攻角与倾角的误差小。下潜过程中,存在轻微的旋转,分析可能是受缆绳及海流的作用,产生轴线方向的力矩。
仪器的摆动会给Pitch和Roll带来较大影响,而对Heading角几乎不会产生影响。但Heading会影响倾角θ在另两个角上的分量。进一步分析摆动情况,选取前35 s数据,对Pitch和Roll角数据去平均值处理,然后通过离散傅里叶变换进行频谱分析,其分布如下:
通过计算倾角波动的基频约为0.188 Hz。从图 11可以看出,随频率增加,两个倾角幅值波动具有一致性,说明仪器此时间段基本同一平面内摆动。但Pitch角的摆动幅值远小于Roll角,结构主要在Roll角方向摆动。
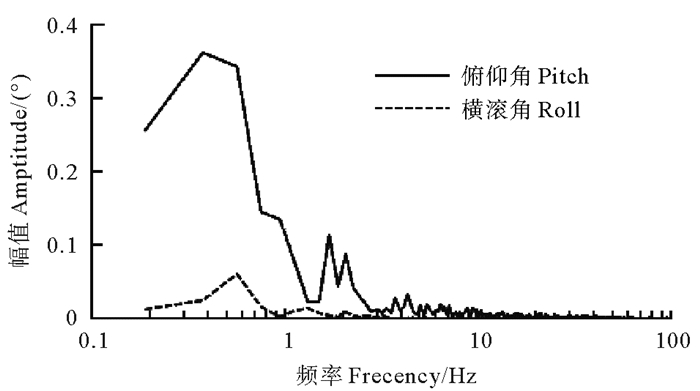
|
图 11 姿态角频谱 Fig. 11 Spectrum of attitude angles |
根据Roll角频谱图,在频率为0.375 Hz处出现峰值,该频率接近于理论计算结构的固有频率0.331 Hz。在低频段(0.188~0.563 Hz),幅值变化较小,在0.26°~0.36°范围内。在大于0.563 Hz后频率出现快速衰减,仪器振动主要为低频的摆动导致。
7 结论本文从理论出发,对影响湍流剖面仪测量结果的几个重要因素进行了分析。并通过实验,对理论结果进行了验证。文中所作的主要工作如下:
(1) 建立双坐标系运动模型,结合倾角、攻角确定双坐标系下各个参数的转换。
(2) 分析下潜速度,可以通过控制配重质量达到下潜速度的配置。
(3) 重浮心距离和下潜速度越大,仪器姿态越稳定。
(4) 结构摆动固有频率随重浮心距离变大而增大,自由摆动在衰减一段时间后呈简谐振动。
(5)通过试验数据,验证了理论计算的准确性,为进一步优化结构提供依据。
| [1] |
姜欣, 刘玉红, 宋诗军, 等. 垂直微结构剖面仪主体结构优化[J]. 中国机械工程, 2015, 26(1): 97-101. Jiang X, Liu H Y, Song S J, et al. Structure optimization for main body of vertical profiler[J]. China Mechanical Engineering, 2015, 26(1): 97-101. (  0) 0) |
| [2] |
康建军, 邬海强, 杨庆轩, 等. 海洋湍流观测技术[J]. 海洋技术, 2007, 26(3): 19-23. Kang J J, Wu H Q, Yang Qi X, et al. Ocean turbulence measurement technology[J]. Ocean Technology, 2007, 26(3): 19-23. (  0) 0) |
| [3] |
王永芳.时、频、波数域下剪切湍流数据分析方法研究[D].青岛: 中国海洋大学, 2014. Wang Y F. Research on Analysis Method of Shear Turbulence Data in Tme, Frequency and Wavenumber Domain[D]. Qingdao: Ocean University of China, 2014. (  0) 0) |
| [4] |
Herminio F N, Rolf L, Yoshiro M, et al. A new quasi-horizontal glider to measure biophysical microstructure[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31: 2278-2293.
(  0) 0) |
| [5] |
Song D L, Yan Q Z, Wang S X, et al. A Method for Ocean Turbulence Effectiveness Detection and Intelligent Processing Based on Pseudo Dissipation Rate[C]. London: Atlantis Press, 2015: 51-54.
(  0) 0) |
| [6] |
刘贵春. 水流作用下圆柱体的涡激振动分析[J]. 科学技术与工程, 2007, 7(1): 22-25. Liu G C. Analysis of vortex-induced vibration of a cylinder in steady flow[J]. Science Technology and Engineering, 2007, 7(1): 22-25. (  0) 0) |
| [7] |
宋诗军.垂直微结构湍流剖面仪结构优化[D].天津: 天津大学, 2013. Song S J. Structure Optimization of Vertical Microstructure Turbulence Profiler[D]. Tianjin: Tianjin University, 2013. (  0) 0) |
| [8] |
王树新, 李晓平, 王延辉, 等. 水下滑翔器的运动建模与分析[J]. 海洋技术, 2005(1): 5-9. Wang S X, Li X P, Wang Y H, et al. Dynamic modeling and analysis of underwater glider[J]. Ocean Technology, 2005(1): 5-9. (  0) 0) |
| [9] |
王子龙, 王延辉, 陈宝阔, 等. 海洋微结构湍流垂直剖面仪设计与试验[J]. 天津大学学报, 2012, 45(3): 279-284. Wang Z L, Wang Y H, Chen B K, et al. Design and application of microstructure turbulence vertical profiler[J]. Journal of Tianjin University, 2012, 45(3): 279-284. (  0) 0) |
| [10] |
兰世泉.垂直微结构湍流剖面仪流致振动分析[D].天津: 天津大学, 2012. Lan S Q. The Flow-induced Vibration Analysis of Microstructure Turbulence Profiler[D]. Tianjin: Tianjin University, 2012. (  0) 0) |
| [11] |
邓绍云. 水流流向对圆柱群阻力特性影响研究[J]. 水运工程, 2009(11): 29-33. Deng S Y. Influence of flow direction on drag force of group cylinder piles flowing around by current[J]. Port and Waterway Engineering, 2009(11): 29-33. (  0) 0) |
| [12] |
王世铮, 杨蒋周. 关于非线性阻尼振动[J]. 大学物理, 1985(10): 12-15. Wang S Z, Yang J Z. Research on nonlinear damped vibration[J]. College Physics, 1985(10): 12-15. (  0) 0) |
 2019, Vol. 49
2019, Vol. 49


