2. 国家海洋局第一研究所 山东 青岛 266061
高频地波雷达是海洋立体监视监测系统中的重要组成部分,可用于运动船只、低空飞行目标的探测,以及流场、风场、浪场等海态信息的提取。雷达的工作频段为3~30 MHz,受到短波电台和短波通讯等射频干扰的影响严重。射频干扰的能量大,严重影响了目标信号的检测和海态信息的提取,甚至会导致接收通道饱和。
为了降低射频干扰的影响,可以通过频率监测,并调整雷达工作频率,以避开射频干扰。但由于短波信号的工作时间和频率都是随机的,选择相对“寂静”的工作频带是比较困难的。因此,针对射频干扰的特点,发展射频干扰抑制技术,减小射频干扰对有效信号的影响,是非常有意义的。
近年来国内外的学者提出了一系列的射频干扰抑制算法。根据射频干扰抑制算法的作用域可以分为时域抑制、频域抑制、空域抑制。在时域进行抑制的有:用AR模型进行预测抑制[1],运用独立分量分析(ICA)方法实现了目标回波与射频干扰的分离[2];在频域进行抑制的有:基于特征子空间的正交投影算法[3-6],利用最小二乘法进行抑制[7];在空域进行抑制的有:借助水平极化辅助天线的空间极化滤波[8-11],高频雷达在射频干扰下的目标探测研究[12]。这些方法对于射频干扰都能起到一定的抑制效果,但是他们都存在一些不足。如AR模型预测算法和时域剔除法适合于射频干扰较弱和持续时间较短的瞬时信号,对于长时间存在并且信号较强的连续电台干扰的抑制性能比较差;斜投影极化滤波方法需要增加一根极化天线,会增加系统的复杂度。实践证明仅在单一作用域对射频干扰进行抑制,效果有限。
在实际工程应用中,考虑到处理流程和计算量等因素,常规的射频干扰抑制流程为对单个通道距离多普勒(RD)谱数据进行处理:选取远距离的射频干扰进行位置和幅值估计;基于单元格对消方法对射频干扰进行抑制[3]。这样做能够直接消除射频干扰,但是由于噪声的影响,会使得近距离目标点出现幅值小于或等于远距离的射频干扰的状况,采用常规的射频干扰抑制会使得目标点被抑制,难以在后续的检测中发现。
本文提出了一种基于方向分解的高频地波雷达射频干扰抑制改进算法,在分析射频干扰特性的基础上,利用射频干扰的方向性特点, 提出了一种先进行方向分解,再在各个方向上进行射频干扰抑制,最后按波束指向进行幅值合成的信号处理方法。该方法对于目标和射频干扰方向不同情况,效果尤其明显。仿真和实测数据验证了方法的有效性。
1 射频干扰特性分析射频干扰混叠在信号回波中通过天线进入雷达系统,与回波信号一起进行处理。
天线接收到信号模型为:
| $ r\left( t \right) = {s_R}\left( t \right) + x\left( t \right) + n\left( t \right), $ | (1) |
式中:sR(t)为发射信号的回波;x(t)为射频干扰信号;n(t)为随机噪声。
通常电台通信等射频干扰为窄带信号,其信号频率变化相对于地波雷达信号为慢变信号,因此可以把射频干扰信号看为一单频信号。由于电台等造成的射频干扰是有源的,在其持续时间内功率基本保持稳定,因此射频干扰强度大并且幅值基本保持稳定。天线阵接收到射频干扰信号,由于到达每个天线的波程不同,波程差产生相位差,第k根天线接收到的射频干扰信号模型表示为:
| $ {x_k}\left( {t, n} \right) = A{{\rm{e}}^{j[2\pi {f_I}\left( {t + nT} \right) + {\varphi _0}]}}{{\rm{e}}^{ -jk\Delta \varphi }}, $ | (2) |
式中:A为射频干扰的振幅;fI为射频干扰的频率;φ0为射频干扰的初相;n为调频周期数,0≤t≤T;T为调频周期;
本文分析的高频地波雷达采用线性调频连续波(FMCW)作为发射信号[5],其信号的模型为:
| $ s\left( t \right) = {{\rm{e}}^{j2\pi ({f_0}t + \frac{1}{2}\alpha {t^2})}}r{\rm{ect}}\left( {\frac{{t-T/2 + nT}}{T}} \right),$ | (3) |
式中:f0为发射信号起始频率;α=B/T为调频斜率;B为调频带宽(Hz)。
接收的信号r(t)经过去载频、去斜、解距离、解速度之后形成了RD谱。由于这一系列运算均为线性运算,因此可以单独对射频干扰x(t)进行上述处理,进一步分析其在RD谱上的特性。
通过单独对射频干扰进行处理,获得射频干扰解速度之后数学模型[5]为:
| $ Z(f, {f_n}) = AD{{\rm{e}}^{j\frac{\pi }{\alpha }(f-{f_{I0}}}}{)^2}{{\rm{e}}^{j({\varphi _0}-k\Delta \varphi )}}\delta ({f_n}-({f_I} - {f_c})), $ | (4) |
式中:
由δ(fn-(fI-fc))可知射频干扰出现在RD谱上的频率位置为fI-fc。根据公式f=αt=(B/T)(2R/c)可知射频干扰在RD谱上每个距离元的幅值为:
| $ \left| {Z(f, {f_n})} \right| = AD{A_a}{A_b}。$ | (5) |
式中:Aa=|ej(φ0-kΔφ)|为常数;
因此式(5)为常数,可知射频干扰在每个距离元的幅值相同,并呈条带状分布。
对解速度后的数据通过DBF在指向角β进行处理,公式如下:
| $ F\left( \beta \right) = \sum\limits_{k = 0}^N {{w_k}{{\rm{e}}^{-j2\pi fdk{\rm{sin}}\beta /c}}}。$ | (6) |
式中:wk为权系数,采用切比雪夫加权;c为光速。
加权后公式如下:
| $ \begin{array}{l} \;\;\;\;Q\left( \beta \right) = \sum\limits_{k = 1}^N {Z(f, {f_n}){w_k}{{\rm{e}}^{-j2\pi fd\left( {k{\rm{-}}1} \right){\rm{sin}}\beta /c}}} = \\ \sum\limits_{k = 1}^N {G{{\rm{e}}^{{\rm{-}}j\left( {k{\rm{ - }}1} \right)2\pi fd/c({\rm{sin}}\beta - {\rm{sin}}\theta )}}} = \\ {\rm{ }}G\frac{{1 - {{\rm{e}}^{{\rm{ - }}jN2\pi fd/c({\rm{sin}}\beta {\rm{ - sin}}\theta )}}}}{{1 - {{\rm{e}}^{ - j2\pi fd/c({\rm{sin}}\beta - {\rm{sin}}\theta )}}}} = \\ {\rm{ }}G{{\rm{e}}^{ - j\left( {N - 1} \right)\pi fd/c({\rm{sin}}\beta - {\rm{sin}}\theta )}}\frac{{{\rm{sin}}(N\pi fd/c({\rm{sin}}\beta - {\rm{sin}}\theta )}}{{{\rm{sin}}(\pi fd/c({\rm{sin}}\beta - {\rm{sin}}\theta )}}。\end{array} $ | (7) |
式中:
由式(7)可知在β=θ时Q(β)取得最大值,因此射频干扰通过DBF进行加权后在其来波方向上幅值最大,其它方向上依次减弱。
由以上理论分析可知,射频干扰在RD谱上通常具有以下特性:干扰强度大,在距离向上具有强相关性,具有方向性,在来波方向上最为明显,而在其它方向上衰减较明显。在实际中,考虑到目标的方向和射频干扰的方向不完全一致,即在不同方向上,射频干扰对目标的影响程度不同。因此,本文的思路是首先进行方向分解,在不同方向上分别抑制射频干扰,然后再进行合成。这样可以最大限度地降低射频干扰抑制对目标的影响。
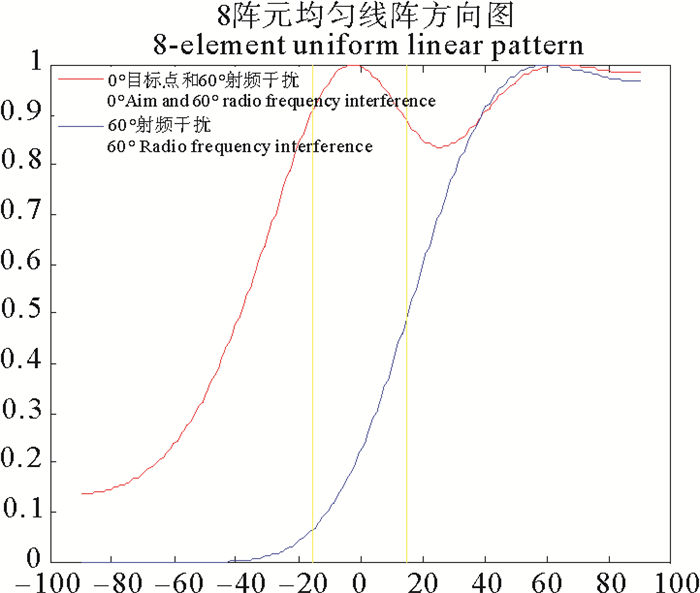
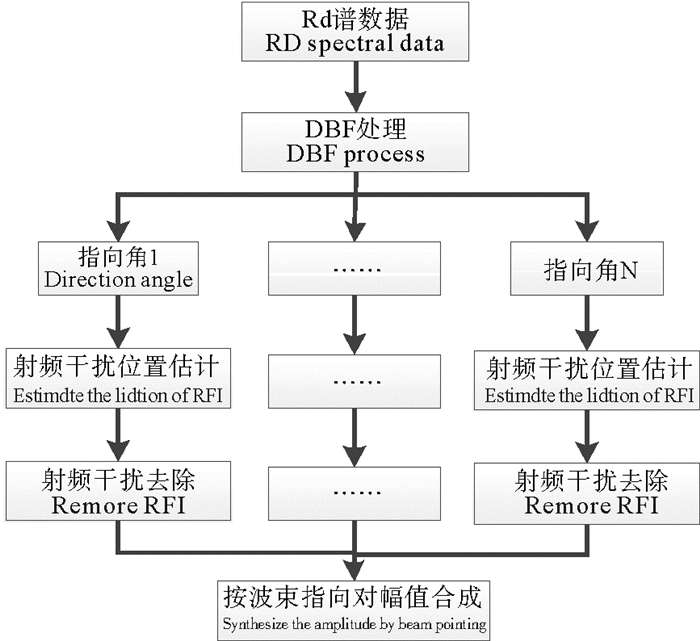
2 改进的射频干扰抑制 2.1 基本流程根据射频干扰具有方向性的特点考虑在方向上对回波数据进行分解,把射频干扰和目标数据进行分离,使目标点所在方向上的数据,射频干扰削弱、目标点增强。如图 1所示在0°目标点所在方向图内射频干扰的幅度值削弱。在RD谱上由于射频干扰在距离向上幅度值的强相关性,并且在所有距离元上均有出现,考虑选取无目标和海态信息的远距离元数据作为预测单元,估计射频干扰的强度和位置信息并在其他距离元上相减消除。在实际工程应用中,改进的射频干扰抑制流程如图 2所示。
|
图 1 目标和射频干扰方向图 Fig. 1 Direction of target and radio frequency interference |
|
图 2 改进后的射频干扰抑制流程 Fig. 2 Improved radio frequency interference suppression process |
对回波数据经过解距离、解速度处理之后获得的RD谱数据通过DBF公式进行加权,获取不同角度内的数据,分解角度数为N,加权公式如式(6)所示。
2.3 射频干扰多普勒频偏位置和幅值估计对每个角度内的数据分别处理,选取远距离处的数据作为估计样本,通过自协方差矩阵对射频干扰的多普勒频偏位置进行估计,通过求均值对射频干扰的幅值进行估计。
获取射频干扰估计样本:
| $ {X_i} = {[{x_i}\left( 1 \right), {x_i}\left( j \right), \ldots, {x_i}\left( n \right)]^{\rm{T}}}。$ | (8) |
式中:xi(j)为第i个距离元第j个多普勒元对应的数值。
构造自协方差矩阵模型:
| $ Q = \frac{1}{M}\sum\limits_{i = 1}^M {{X_{i}}X_i^{\rm{T}}} 。$ | (9) |
式中:M为获取远距离单元格的样本数量。
对Q进行特征值分解,把特征值按大小排列,得到λ1>λ2>…>λn。由于射频干扰强度很大,因此寻找特征值明显大的位置,对应于射频干扰出现的多普勒频偏位置。
获取射频干扰的幅值:
| $ \hat Y = \frac{1}{M}\sum\limits_{i = 1}^M {{P_i}} 。$ | (10) |
式中:Pi=[pi(1), pi(j), …, pi(n)],在射频干扰出现的频率元,pi(j)=xi(j);在不含射频干扰的频率元,pi(j)=0。
2.3 射频干扰去除在RD谱上,由于射频干扰在距离向上具有强相关性,远距离单元估测出的射频干扰的幅值和近距离元上的幅值相同,因此在近距离单元上通过相减则可以去除射频干扰并不对回波中的目标和海态信息造成影响:
| $ {Y_0} = Y-\hat Y。$ | (11) |
式中:Y0为去除射频干扰后幅值;Y为近距离单元幅值。
2.4 按波束指向对幅值合成按上述方法对每个小角度内的数据分别进行射频干扰抑制,在实际工程应用中,我们不可能对每个小角度内的目标点进行检测分析,由于我们通过DBF对每个角度进行加权分解时,只是改变目标点、海杂波、地杂波、射频干扰的幅度值,对其位置没有变化,因此我们可以直接对所有抑制射频干扰后的数据按波束指向对幅值进行求和,对所有的目标点信息进行融合使k个通道的数据变为k-1个波束的数据。如上图 1黄线标示内的各个角度数据进行合成,以方便目标点的检测和后续信息处理,合成公式如下式:
| $ G\left( b \right) = \sum\limits_{d = \frac{{1 + N\left( {b-1} \right)}}{{k-1}}}^{\frac{{Nb}}{{k-1}}} {{Y_{0d}}} 。$ | (12) |
式中:G为合成后各个波束的RD谱数据,1 < b≤k-1,b为整数;Y0d为射频干扰抑制后第d个角度内的RD谱数据。
通过以上步骤,就可以抑制回波数据中掺杂的射频干扰,并保留其中目标和海态信息,发现射频干扰掩藏下的目标信号,并提高目标的信干比。
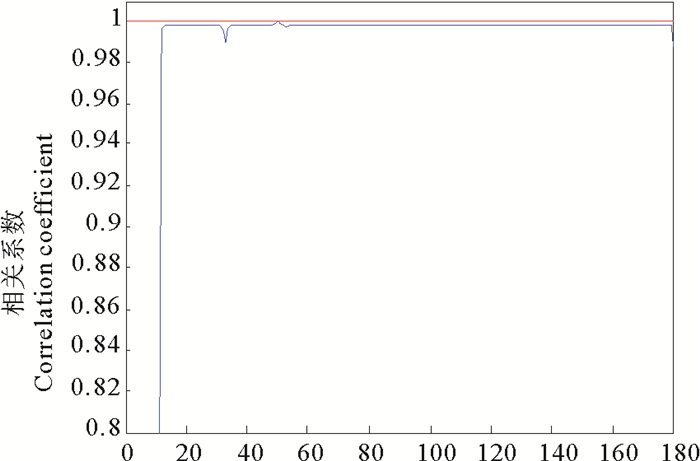
3 实验结果分析 3.1 距离强相关性验证根据上述分析射频干扰在距离向上具有很强的相关性,由于这个性质对射频干扰实际抑制效果有重要的影响。因此我们选取含有射频干扰的实测数据进行验证,取包含射频干扰但不包含海杂波部分的频偏数据作为观测样本数据,求各个距离元与参考距离元的相关性(参考距离元为在距离单元上随机选取,此时选取第50距离元),相关系数如图 3所示,因为前10个距离单元为高频地波雷达盲区不予考虑,可见相关系数均在0.98以上, 通过实际数据证明了射频干扰在距离域上的强相关性,因此我们可以选择远距离单元的信号作为纯的射频干扰信号样本进行估计。
|
图 3 射频干扰各距离元相关性 Fig. 3 Correlation between various distance elements of radio frequency interference |
本节通过仿真验证两个问题:(1)验证射频干扰和目标点来波方向不同时的抑制效果;(2)验证同时有多个来波方向的射频干扰时的抑制效果。仿真的方法是在实测数据背景上,仿真产生射频干扰和目标船只信号,进行抑制方法验证。具体设计了如下三个仿真实验。
实验一 目标与射频干扰来自同一方向的干扰抑制效果仿真。添加一仿真目标其坐标为:频偏0.09 Hz,距离元44,方向0度。同时添加一相同频偏的射频干扰对目标点进行掩盖并覆盖整条频带,方向0度。采用本文所述方法对射频干扰进行抑制,实验结果如图 4a、b所示。

|
图 4 单源射频干扰仿真实验结果 Fig. 4 The simulation experiment results of single source radio frequency interference |
实验二 目标与射频干扰来自不同方向的干扰抑制效果仿真。仿真目标点和背景均和实验一相同,依次更改射频干扰的方向为10、20、30、40度。采用本文所述方法对射频干扰进行抑制,实验结果如图 4c(射频干扰方向为30度),表 1所示。
|
|
表 1 不同方向射频干扰抑制结果 Table 1 Radio frequency interference suppression results in different directions |
结果分析 图 4b、c显示本文所述方法对不同方向射频干扰均有良好的抑制效果。选取仿真目标点位置距离元进行对比分析,结果如图 4d所示。对于来波方向不同的射频干扰具有更好的抑制效果(提高8.7dB)。
实验三 多源射频干扰抑制效果仿真。增加三条来自不同方向的射频干扰,其坐标分别为:频偏-0.13 Hz,方向15度;频偏-0.1 Hz,方向-10度;频偏0.09 Hz,方向25度。添加射频干扰覆盖下的目标点,均为第44个距离元,方向均为0度。采用本文所述方法对射频干扰进行抑制,实验结果如图 5所示。

|
图 5 多源射频干扰仿真数据实验结果 Fig. 5 The simulation experiment results of multi-source radio frequency interference |
结果分析 抑制前和抑制后的RD谱分别如图 5a、b所示,表明此抑制方法对多个来波方向的射频干扰仍然具有良好的抑制效果。
3.3 实测数据验证及分析选取高频地波雷达对黄海某海域的实际监测数据中获取的带有射频干扰的数据进行实验,并将上述抑制算法和常规射频干扰抑制算法进行性能比较。
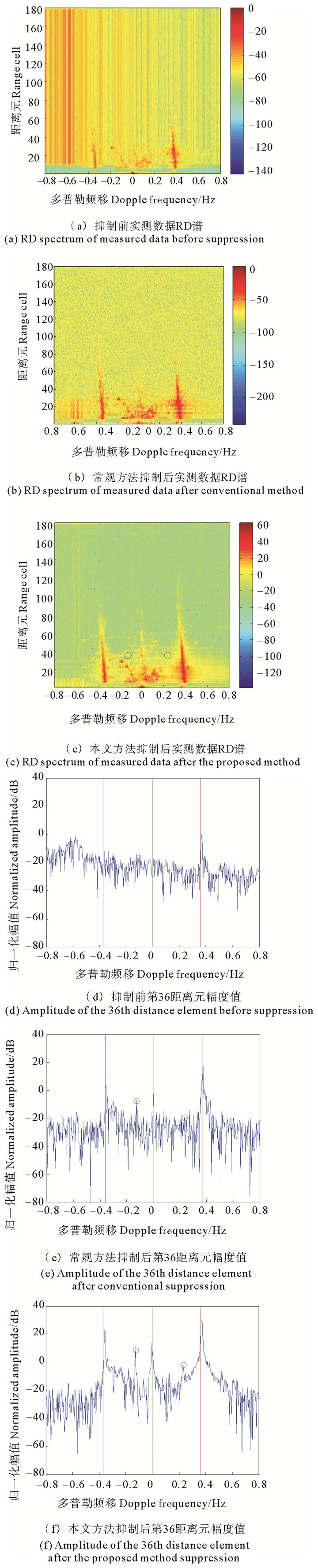
如图 6a为抑制前数据,数据被大片射频干扰污染。图 6b为采用常规基于单元格对消方法抑制后的数据,图 6c为采用本文方法抑制后的数据。我们可以看到采用上述两种方法射频干扰都能够被抑制,但是本文提出方法射频干扰抑制更加彻底,目标信息获得了保留并且幅度值获得了增强。选取其中第36个距离元进行分析并进行归一化处理,未抑制前的数据如图 6d所示,常规方法抑制后的数据如图 6e所示,本文采用方法抑制后的数据如图 6f所示,绿线显示地杂波所在位置,两条红线分别显示海杂波所在位置。由图可知,被射频干扰掩盖的地杂波和海杂波信息,在射频干扰抑制后直接显示出来,如图 6f所示在-0.127和0.233 5 Hz频偏位置显示出被射频干扰掩盖下的目标点(用红色圆圈标出),比周围背景提高约20 dB。通过图 6e、f对比,可以看出本文提出方法比常规方法滤除射频干扰后目标信息更加易于提取。
|
图 6 雷达实测数据实验结果 Fig. 6 Experimental results of radar measured data |
本文通过分析高频地波雷达数据处理流程,推导了射频干扰在RD谱上的表现形式,得出了射频干扰在RD谱的距离向上幅度具有强相关性,在射频干扰的来波方向上幅度达到最大。由此对常规通过单通道射频干扰抑制方法进行改进,提出了一种基于方向分解的射频干扰抑制方法。采用仿真和实测数据进行验证,结果表明该方法能够有效的进行射频干扰抑制,并且减小抑制过程中对目标幅值信息的影响。
| [1] |
许瑜昀, 文必洋, 吴雄斌, 等. 基于短时傅立叶变换的高频地波雷达射频干扰抑制[J]. 武汉大学学报:理学版, 2004, 50(5): 645-648. Xu Yuyun, Wen Biyang, Wu Xiongbin, et al. Radio frequency interference suppression in high frequency surface wave radar based on the short time Fourier transform[J]. Journal of Wuhan University: Nature Science Edition, 2004, 50(5): 645-648. (  0) 0) |
| [2] |
王赞, 陈伯孝, 张各各. 高频地波雷达射频干扰分离方法研究[J]. 电波科学学报, 2012(4): 12-16. Wang Chan, Chen Boxiao, Zhang Gege. High frequency surface wave radar radio frequency interference separation method research[J]. Journal of Radio Science, 2012(4): 12-16. (  0) 0) |
| [3] |
牛炯, 黎明, 张玲, 等. 基于距离-多普勒谱的高频地波雷达的射频干扰抑制[J]. 中国海洋大学学报(自然科学版), 2014, 44(12): 163-170. Niu Jiong, Li Ming, Zhang Ling, et al. Radio interference suppression in high frequency surface wave radar based on Range-Doppler spectrum[J]. Periodical of Ocean University of China, 2014, 44(12): 163-170. (  0) 0) |
| [4] |
Wang W, Wyatt L R. Radio frequency interference cancellation for sea-state remote sensing by high-frequency radar[J]. Iet Radar Sonar Navigation, 2011, 5(4): 405-415. DOI:10.1049/iet-rsn.2010.0041
(  0) 0) |
| [5] |
Hao Z, Wen B. Radio frequency interference suppression in small-aperture high frequency radars[J]. Electronics Letters, 2012, 39(12): 925-927.
(  0) 0) |
| [6] |
Juhel B, Vezzosi G, Goff M L. Radio frequency interferences suppression for ultra wide band radar[C]//. Signal Processing Conference(EUSIPCO 1998), 9th European. IEEE, 1998.
(  0) 0) |
| [7] |
Holdsworth D A. Over-the-horizon radar continuous-wave interference suppression using harmonic least-squares fitting[C]//. International Conference on Radar, 2013: 106-111.
(  0) 0) |
| [8] |
王祎鸣, 毛兴鹏, 洪泓, 等. 基于斜投影算子的高频雷达窄波束形成方法[J]. 电波科学学报, 2015, 30(5): 16-19. Wang Yiming, Mao Xingpeng, Wang Hong, et al. Narrow beam forming method for high frequency radar based on oblique projection operator[J]. Journal of Radio Science, 2015, 30(5): 16-19. (  0) 0) |
| [9] |
刘爱军, 毛兴鹏, 邓维波. 基于斜投影极化滤波的高频雷达电台干扰抑制[J]. 吉林大学学报(工学版), 2011, 41(4): 1177-1182. Liu Aijun, Mao Xingpeng, Deng Weibo. Interference suppression of high frequency radar radio station based on oblique projection polarization filter[J]. Journal of Jilin University(Engineering Edition), 2011, 41(4): 1177-1182. (  0) 0) |
| [10] |
Leong H. Adaptive nulling of skywave interference using horizontal dipole antennas in a coastal surveillance HF surface wave radar system[C]. //Radar IET, 1997: 26-30.
(  0) 0) |
| [11] |
杨俊, 文必洋, 吴世才, 等. 用水平天线消除天波干扰的算法研究[J]. 电波科学学报, 2004, 19(2): 176-181. Yang Jun, Wen Biyang, Wu Shicai, et al. Study on the algorithm of eliminating sky-wave interference using horizontal antenna[J]. Journal of Radio Science, 2004, 19(2): 176-181. (  0) 0) |
| [12] |
周浩, 文必洋, 吴世才. 高频雷达在射频干扰下的目标探测研究[J]. 现代雷达, 2004, 26(9): 29-32. Zhou Hao, Wen Bi Yang, Wu Shicai. Research on target detection of high frequency radar under the condition of the radio frequency interference[J]. Modern Radar, 2004, 26(9): 29-32. (  0) 0) |
2. The First Institute of Oceanography, Qingdao 266061, China
 2018, Vol. 48
2018, Vol. 48


